Эффект Зельдовича-Сюняева

Космическое микроволновое фоновое излучение (CMB) – электромагнитное излучение, заполняющее Вселенную, обладающее высокой степенью изотропности и спектром характерным для черного тела с температурой 2.73K. CMB было открыто в1965 г. Пензиасом и Вильсоном.
В 1965 г впервые был открыт внегалактический рентгеновский протяженный источник. Позиция этого источника совпадает со скоплением галактик Coma (красное смещение z=0.023). В статье Felten et al. (1966), авторы предположили, что это излучения происходит вследствие тормозного излучения горячего газа с температурой 10^8 K заполняющего пространство между галактиками в скоплении. В 1970х г. наблюдения линии гелиеподобного железа (потенциал ионизации 8.8 кэВ) в спектре скопления доказали присутствие горячего газа в скоплениях.
При рассеянии фотона на покоящемся электроне частота фотона уменьшается (эффект Комптона). Но при рассеянии на движущемся электроне частота фотона может увеличиваться, этот эффект известен как обратное комптоновское рассеяние. Электроны в скоплении галактик движутся со скоростями близкими к тепловой скорости газа. Этот эффект использовался Р. Сюняевым (выпускником ФОПФ МФТИ) и Я. Зельдовичем в 1969 г для оценки искажения спектра СМВ при прохождении этого излучения сквозь горячий газ скоплений. Эффект искажения спектра CMB вследствие такого взаимодействия носит их имена. Изменение частоты фотонов из-за рассеяния на движущихся электронах среднем положительно, т.е. такое рассеяние приводит к увеличению частоты фотонов.

Clusters of Galaxies (Coma-optical image)

Images of the Coma Cluster
optical emission
Radio emission
X-rays (Chandra) 0.1-10 keV
(Einstein) 8.0-8.2 keV

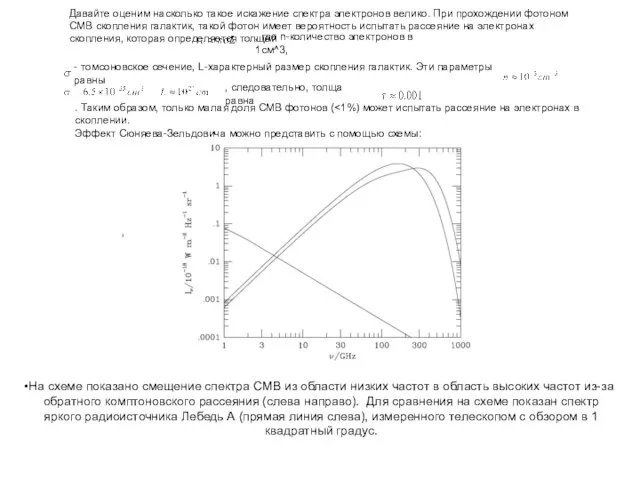
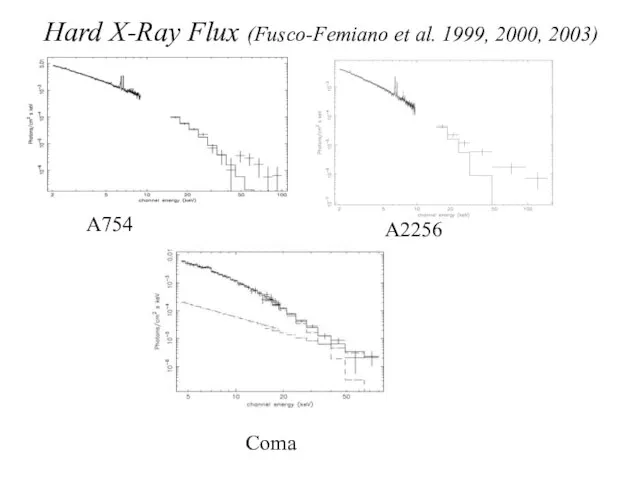
На схеме показано смещение спектра CMB из области низких частот в область высоких частот из-за обратного комптоновского рассеяния (слева направо). Для сравнения на схеме показан спектр яркого радиоисточника Лебедь А (прямая линия слева), измеренного телескопом с обзором в 1 квадратный градус.
Давайте оценим насколько такое искажение спектра электронов велико. При прохождении фотоном CMB скопления галактик, такой фотон имеет вероятность испытать рассеяние на электронах скопления, которая определяется толщей
, где n-количество электронов в 1см^3,
- томсоновское сечение, L-характерный размер скопления галактик. Эти параметры равны
,
, следовательно, толща равна
. Таким образом, только малая доля CMB фотонов (<1%) может испытать рассеяние на электронах в скоплении.
Эффект Сюняева-Зельдовича можно представить с помощью схемы:

Вычислим среднюю энергию, которую фотон получает при рассеянии на тепловом электроне. Из лекции по комптоновскому рассеянию известно, что мощность комптоновских потерь электроном равна
В нерелятивистском пределе и .
Среднее число фотонов рассеивающих в одну секунду на электроне равно
где частота в знаменателе – средняя частота фотонов .
Средняя энергия, получаемая фотонов при рассеянии в нерелятивистском пределе равна
Следовательно, искажение спектра вследствие обратного комптоновского рассеяния представимо в виде
где g – безразмерная спектральная функция, которая будет вычислена ниже, неискаженный спектр CMB.
Определим параметр комптонизации как
Для скопления с температурой 5 кэВ параметр комптонизации по порядку величины равен .

Давайте рассмотрим аналитический вывод спектра искажения CMB.
Р. Сюняев и Я. Зельдович вычислили спектральную функцию g(x) используя работу А. Компанейца (1956). Ниже приводиться вывод уравнения Компанейца.
Кинетическое уравнение на плотность фотонов в однородной среде имеет вид
где электрон-фотонное сечение рассеяния, n – функция распределения фотонов, N – функция распределения электронов. Число случаев рассеяния фотонов с частотой в частоту описывается слагаемым .
Пропорциональность и следует из общих соображений, множитель учитывает спонтанное и вынужденное излучения. Фотоны описываются статистикой Бозе-Эйнштейна, а электроны – статистикой Больцмана.
Уравнение Компанейца выводится в приближении, что изменение частоты фотона мало и в этом случае можно воспользоваться разложением в ряд Тейлора:
где было использовано и . Температура CMB обозначена T, а температура электронов как . Предел справедлив для случая рассеяния CMB фотонов на электронах скопления с температурой несколько кэВ.

После подстановки этих выражений в кинетическое уравнение
(*)
где
Начнем с вычисления второго интеграла. Для этого заметим следующее.
Законы сохранения энергии и импульса для комптоновского рассеяния имеют вид
Решая эти уравнения и учитывая малость изменения частоты фотона, получаем
В нерелятивистском пределе важны только первые слагаемые в числителе и знаменателе, поэтому
Подставляя во второй интеграл, находим

Угловой интеграл равен
Окончательно, второй интеграл равен
Уравнения (*) может быть упрощено, когда и записано в виде
(**)
Так как количество фотонов сохраняется при рассеянии, то
подставляя в это уравнение выражение (**) и интегрируя по частям, находим, что
откуда находим выражение для первого интеграла.
Перепишем (**) подставляя значения интегралов
Находим уравнение Компанейца для эффекта Сюняева-Зельдовича на скоплении галактик

Подставляем спектр Планка в правую часть уравнения и находим выражение для возмущения спектра CMB после дифференцирования
где y-параметр комптонизации (см. начало лекции).
Запишем выражение для искажения интенсивности
Характерный измеренный спектр возмущения имеет вид (сплошная кривая)

Кинематический Сюняев-Зельдович эффект

Hard X-Ray Flux (Fusco-Femiano et al. 1999, 2000, 2003)
A754
Coma
A2256