ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК

ПИФАГОР
ФАЛЕС

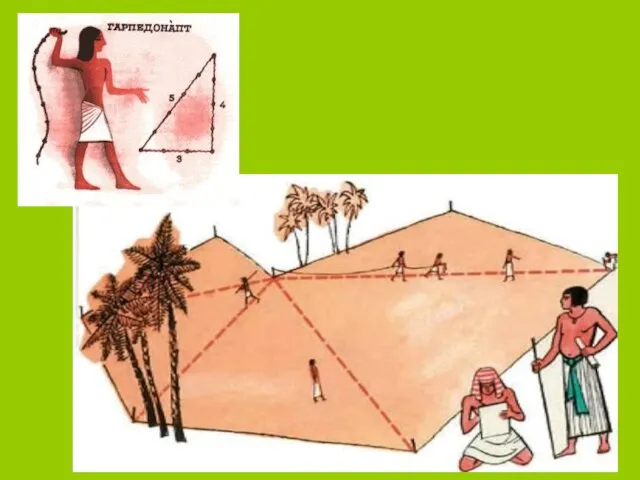
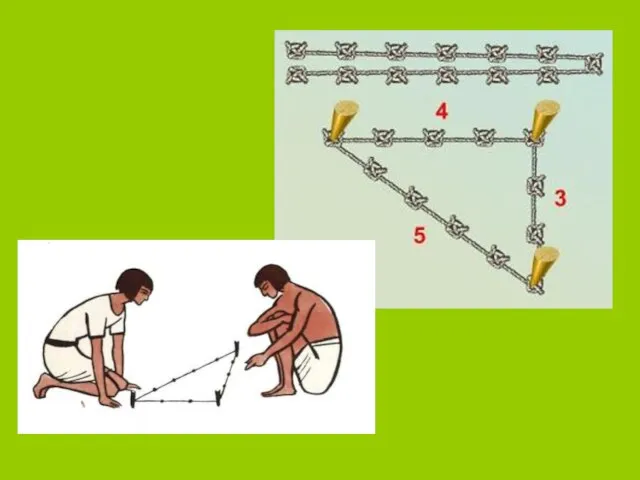
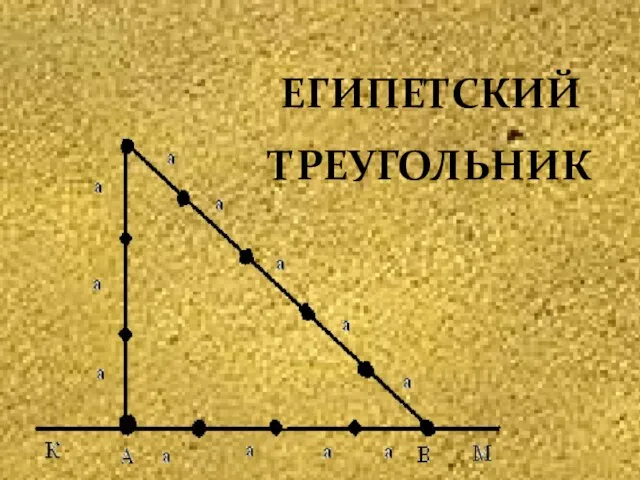
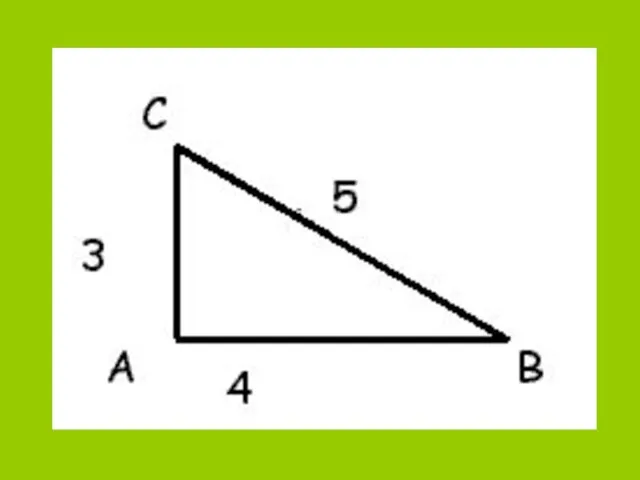
ЕГИПЕТСКИЙ
ТРЕУГОЛЬНИК

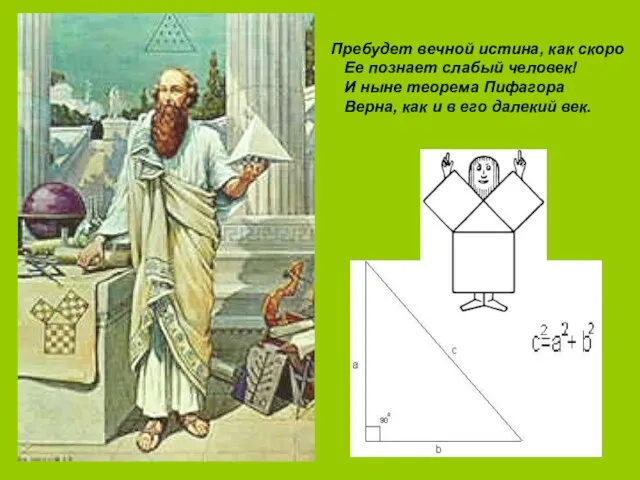
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.

Особенностью треугольника,
известной ещё со времён античности, является то,
что при таком отношении сторон
теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы,
то есть 9:16:25.

Задача индийского математика XII века Бхаскары:
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв го ствол обломал
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?»

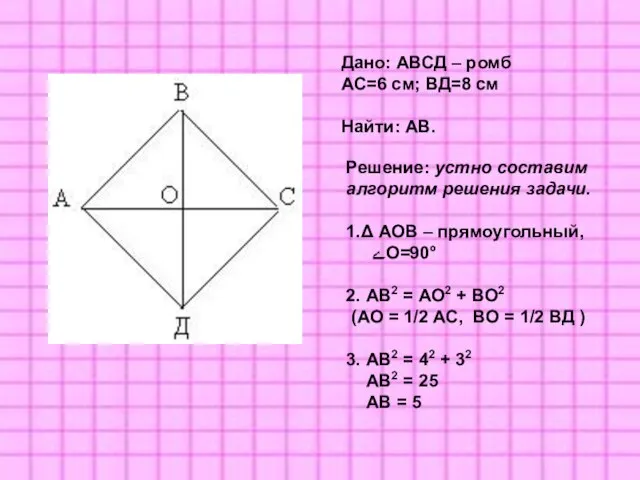
Дано: АВСД – ромб
АС=6 см; ВД=8 см
Найти: АВ.
Решение: устно составим алгоритм решения задачи.
1.Δ АОВ – прямоугольный,
ےO=90°
2. АВ2 = АО2 + ВО2
(АО = 1/2 АС, ВО = 1/2 ВД )
3. АВ2 = 42 + 32
АВ2 = 25
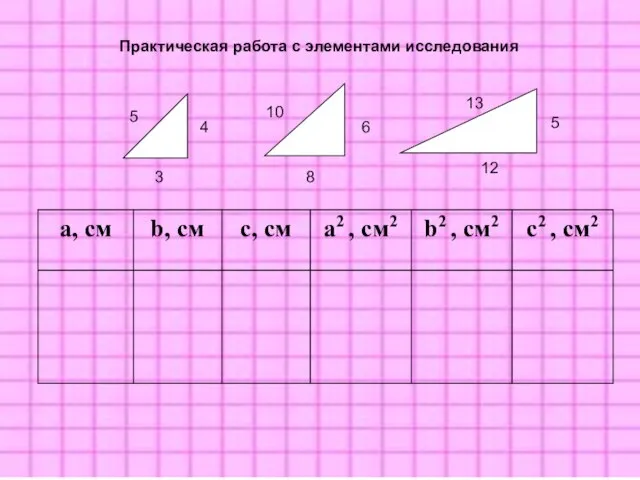
АВ = 5

8
6
10
5
4
3
13
12
5
Практическая работа с элементами исследования

Если катеты и гипотенузу какого-нибудь целочисленного прямоугольного треугольника обозначить буквами х, у и z, то по теореме Пифагора получим:
x2+y2=z2. (1)
Оказывается, что верно и обратное, т. е. если х, у и z — натуральные числа, удовлет­воряющие уравнению (1), то треугольник со сторонами х, у и z — прямоугольный.
Целочисленный прямоугольный треуголь­ник для краткости иногда называют пифагоровым.

Стоит треугольник, как ментор,
И угол прямой в нем есть.
И всем его элементам
Повсюду покой и честь.
Прелестная гипотенуза
Внеслась так смело ввысь!
И с нею в вечном союзе
Два катета тоже взвились.
И всё на торжищах света,
Как в огненном кольце
И все повторяют это:
«Ах, а2, b2, с2»
И даже в холодной медузе
Огонь эта песня зажгла,
И всё это гипотенузы
И катетов двух дела!
Монета с изображением Пифагора

Ментор — персонаж древнегреческой мифологии с острова Итаки — персонаж древнегреческой мифологии с острова Итаки — сын Алкима — персонаж древнегреческой мифологии с острова Итаки — сын Алкима, старый друг Одиссея — персонаж древнегреческой мифологии с острова Итаки — сын Алкима, старый друг Одиссея, поручившего Ментору заботы о доме и хозяйстве, отправляясь в Трою — персонаж древнегреческой мифологии с острова Итаки — сын Алкима, старый друг Одиссея, поручившего Ментору заботы о доме и хозяйстве, отправляясь в Трою. Поэтому Ментор старался препятствовать назойливым женихам Пенелопы — персонаж древнегреческой мифологии с острова Итаки — сын Алкима, старый друг Одиссея, поручившего Ментору заботы о доме и хозяйстве, отправляясь в Трою. Поэтому Ментор старался препятствовать назойливым женихам Пенелопы; он же был воспитателем Телемаха, сына Одиссея.