«Электромагнитные гармонические колебания и их математическое обоснование». Урок изучения нового материала, интегрированный уро
Содержание
- 2. Цель учебная: Сформировать у студентов понятие «гармоническое колебание» и научить определять параметры колебаний математическими способами. Задачи
- 3. Формы и методы обучения беседа; рассказ; объяснительно-иллюстрационный: проблемные ситуации: метод суждения.
- 4. Структура занятия: Актуализация знаний. Мотивация учебной деятельности. Постановка цели. Формирование новых знаний. Контроль полученных знаний. Подведение
- 5. Актуализация раннее усвоенных знаний. Преподаватель физики задает вопросы студентам: Что собой представляют колебания? В каких разделах
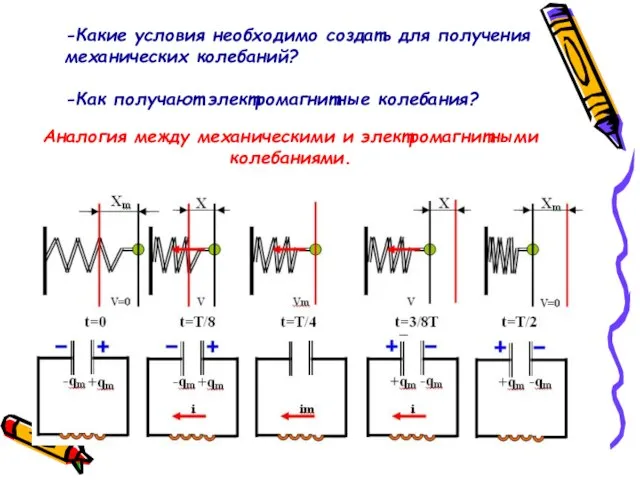
- 6. Аналогия между механическими и электромагнитными колебаниями. -Какие условия необходимо создать для получения механических колебаний? -Как получают
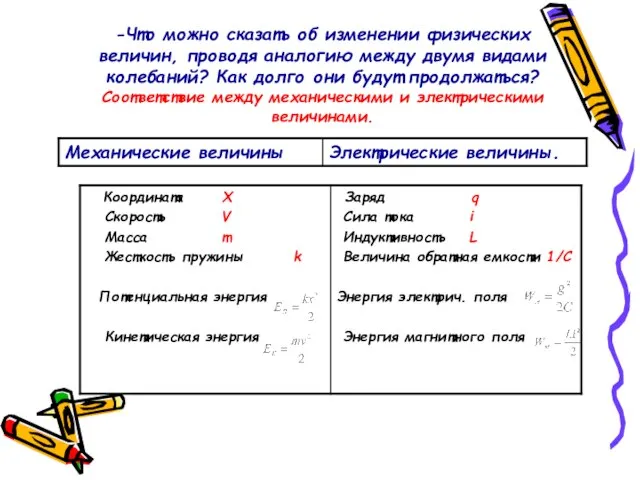
- 7. -Что можно сказать об изменении физических величин, проводя аналогию между двумя видами колебаний? Как долго они
- 8. Мотивация учебной деятельности Преподаватель физики отмечает, что колебания свойственны всем явлениям природы: пульсируют звезды, вращаются планеты,
- 9. Постановка цели урока Правильно ответить на поставленный вопрос вам поможет изучение явлений «гармонические колебания в физике».
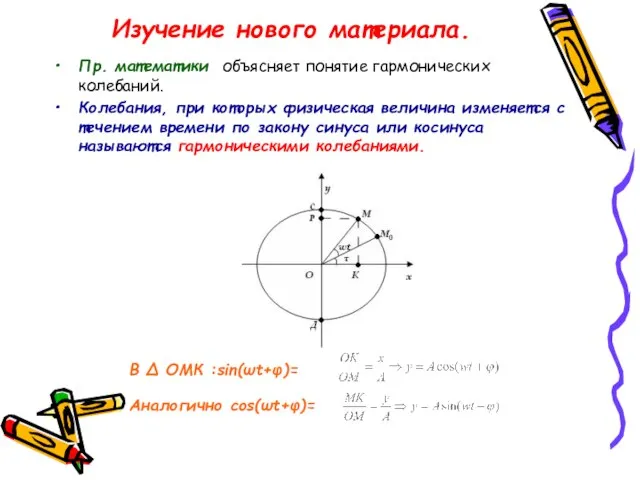
- 10. Изучение нового материала. Пр. математики объясняет понятие гармонических колебаний. Колебания, при которых физическая величина изменяется с
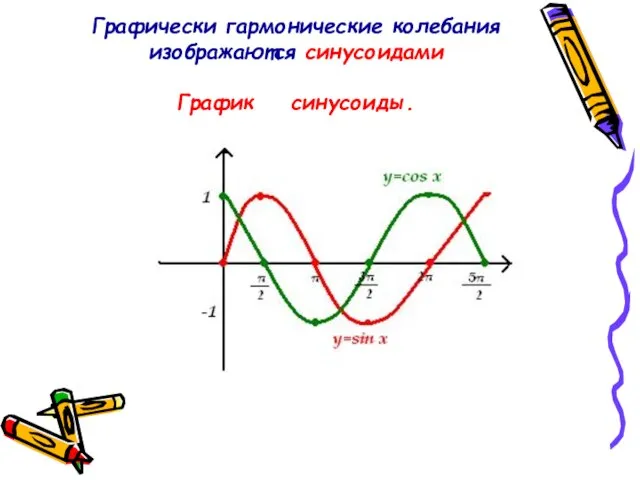
- 11. Графически гармонические колебания изображаются синусоидами График синусоиды.
- 12. Пр. физики предлагает студентам объяснить : «Почему колебания груза на пружине и свободные колебания в закрытом
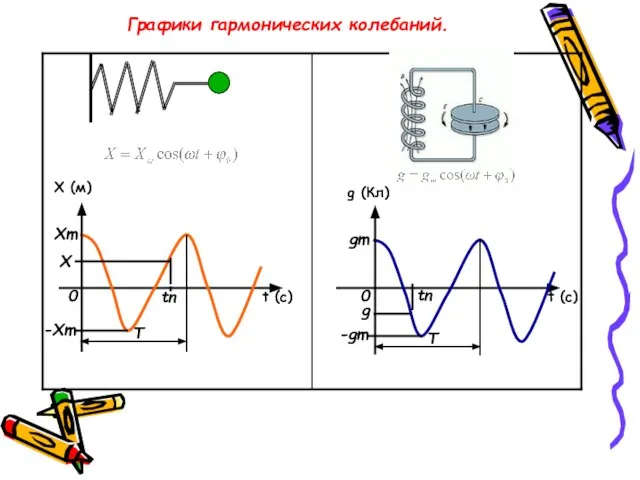
- 13. Графики гармонических колебаний. Х (м) t (c) g (Кл) t (c) Хm -Хm 0 0 tn
- 14. Пр. математики, используя уравнения гармонических колебаний и их графики, вводит понятие гармонических колебаний. , Параметры гармонических
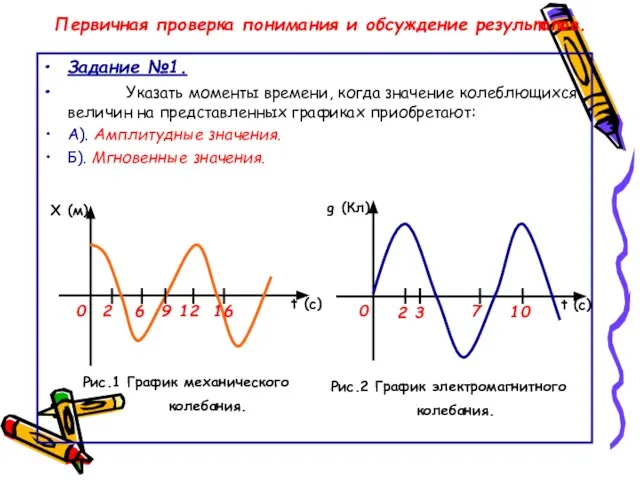
- 15. Первичная проверка понимания и обсуждение результатов. Задание №1. Указать моменты времени, когда значение колеблющихся величин на
- 16. Изучение нового материала. Параметры гармонических колебаний. Пр. математики: 3. Минимальный промежуток времени, в течении которого значение
- 17. Параметры гармонических колебаний. Пр. математики: 4. Величина обратная периоду называется частотой колебания. - частота колебания. Пр.
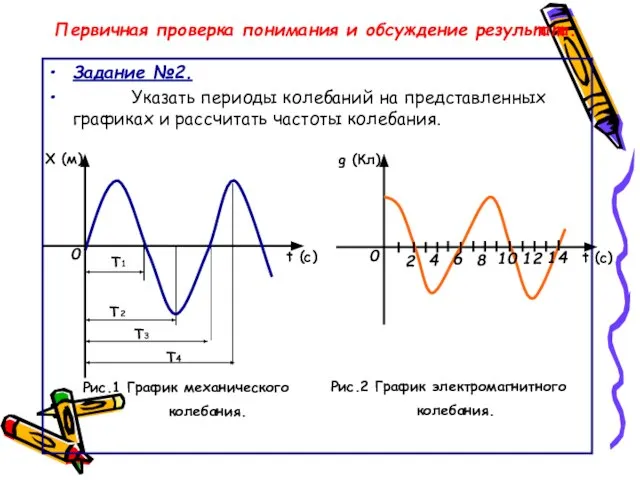
- 18. Первичная проверка понимания и обсуждение результата. Задание №2. Указать периоды колебаний на представленных графиках и рассчитать
- 19. Изучение нового материала. Пр. математики: Из курса математики известно, что наименьшим периодом функции косинуса и синуса
- 20. Пр. математики: 6. Выражениение, которое стоит под знаком синуса или косинуса в уравнении гармонического колебания, называется
- 21. Пример расчета разности фаз. Уравнение изменения заряда конденсатора по закону косинуса: Уравнение изменения заряда конденсатора по
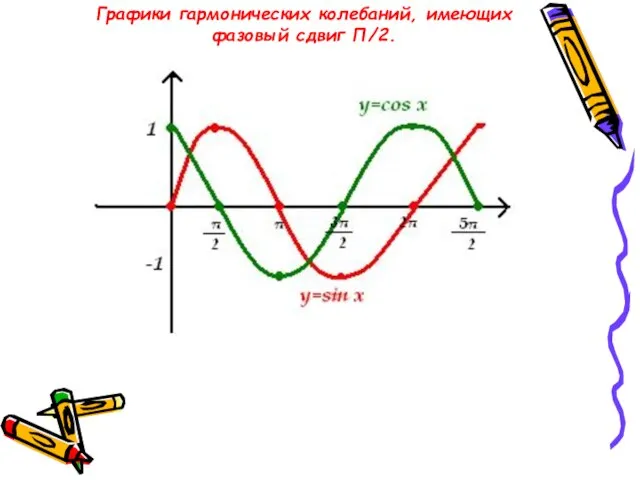
- 22. Графики гармонических колебаний, имеющих фазовый сдвиг П/2.
- 23. Пр. математики.
- 25. Подведение итогов занятия. Пр. физики. У студентов сформировалось понятие электромагнитного гармонического колебания, они убедилась в наличии
- 27. Скачать презентацию
















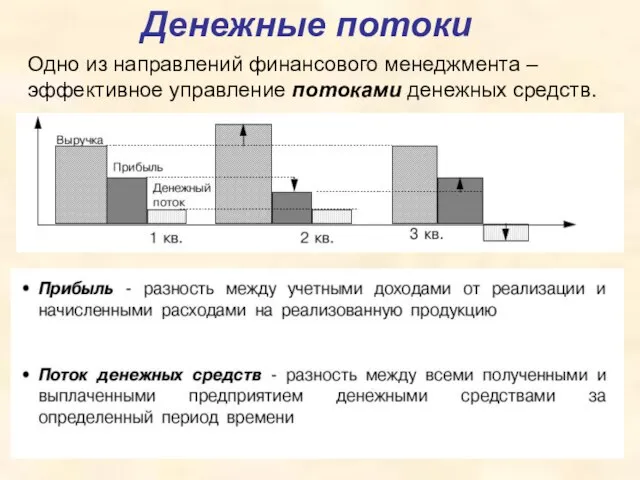 Денежные потоки
Денежные потоки ПрофессииXXI века
ПрофессииXXI века Презентация на тему Вербное Воскресенье
Презентация на тему Вербное Воскресенье  Бокс и борьба как основные виды силовых состязаний
Бокс и борьба как основные виды силовых состязаний Презентация на тему Окружность. Её центр и радиус 2 класс
Презентация на тему Окружность. Её центр и радиус 2 класс  Некоторые матричные операции в MS Excel
Некоторые матричные операции в MS Excel Министерство сельского хозяйства Российской Федерации ФГОУ ВПО «Оренбургский государственный аграрный университет» Институт до
Министерство сельского хозяйства Российской Федерации ФГОУ ВПО «Оренбургский государственный аграрный университет» Институт до Мирас-собиратель, хранитель, проводник культурных традиций
Мирас-собиратель, хранитель, проводник культурных традиций Лёгкая атлетика. Прыжки в длину
Лёгкая атлетика. Прыжки в длину Устройство компьютера.(3-4 класс)
Устройство компьютера.(3-4 класс) Пельмени
Пельмени Михаил Булгаков Личность. Творчество
Михаил Булгаков Личность. Творчество Три функции денег
Три функции денег Возможности сервисов Web 2.0 для сетевого взаимодействия педагогов
Возможности сервисов Web 2.0 для сетевого взаимодействия педагогов Тормозные стенды BT 6xx
Тормозные стенды BT 6xx Другие войска. Состав и предназначение
Другие войска. Состав и предназначение Изменения в методическом обеспечении финансирования в связи с введением ФГОС НОО И.В.АбанкинаДиректор Института развития образ
Изменения в методическом обеспечении финансирования в связи с введением ФГОС НОО И.В.АбанкинаДиректор Института развития образ НОВЫЕ ВОЗМОЖНОСТИ ПЕНСИОННОЙ РЕФОРМЫ
НОВЫЕ ВОЗМОЖНОСТИ ПЕНСИОННОЙ РЕФОРМЫ Презентация на тему Станислав Гроф
Презентация на тему Станислав Гроф Офис в облаках
Офис в облаках Aqualoq. Toilet bowl new age. Features & benefits
Aqualoq. Toilet bowl new age. Features & benefits Презентация на тему Битва на Чудском озере
Презентация на тему Битва на Чудском озере  Викторина по сказкам для малышей
Викторина по сказкам для малышей Генетические алгоритмы
Генетические алгоритмы Самооценка как инструмент определения проблем системы управления
Самооценка как инструмент определения проблем системы управления Концептуальные основания метода проектов и основные понятия
Концептуальные основания метода проектов и основные понятия ЧС. Практика 3 тема
ЧС. Практика 3 тема Ярмарка народных промыслов России
Ярмарка народных промыслов России