Слайд 2 Электромагнитный момент. Электромагнитный момент определяется: М = kФI.
Таким образом, электромагнитный момент пропорционален

основному магнитному потоку и току и также не зависит от формы кривой распределения индукции в воздушном зазоре.
Слайд 31.8. Уравнения электромеханического преобразования энергии
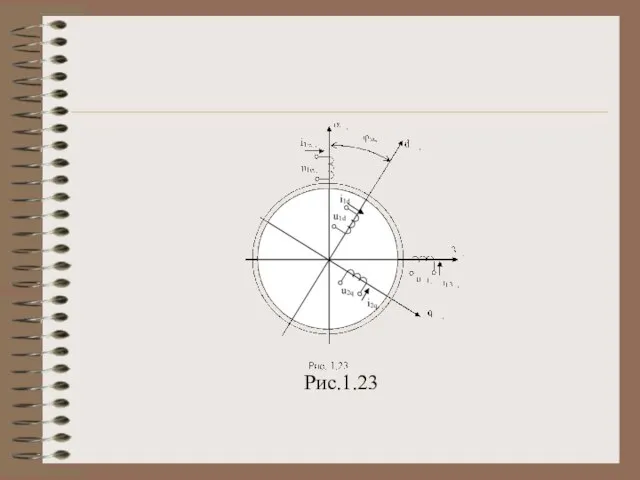
Рассмотрим двухфазную двухполюсную ЭМ, имеющую 2 ортогональные системы

обмоток. Принята следующая индексация: 1 – статорные параметры, 2 – роторные параметры; - система координат жестко связанная со статором; d, q - система координат, жестко связанная с ротором (рис. 1.23).
Слайд 5 Динамика обобщенной машины описывается 4 уравнениями электрического равновесия в цепях ее обмоток

и уравнением электромеханического преобразования энергии, которое выражает электромагнитный момент ЭМ как функцию электрических и механических координат системы.
Слайд 6 на основании второго закона Кирхгофа и закона Фарадея можно записать следующую систему

координат для каждой из четырех пар зажимов
(1.5)
Слайд 7 где - закон Фарадея (наведенная ЭДС прямо пропорциональна изменению потосцепления)
Уравнения (1.5)

записаны для реальных напряжений, токов и параметров обобщенной машины , т.е. для обмоток статора в осях , неподвижных относительно статора, а для ротора – в осях координат d,q,0 , неподвижных относительно ротора.
Слайд 8Уравнения системы (1.5) однотипны и их можно записать в обобщенной форме:
Потокосцепление каждой

обмотки в общем виде определяется результирующим действием токов всех обмоток ЭМ (система (1.6):
Слайд 10 В системе уравнений (1.6) первая часть индекса у индуктивности указывает в какой

обмотке наводится ЭДС, а вторая – током какой обмотки она наводится. Например L2d,2d – собственная индуктивность фазы d ротора, а L2d,2q – взаимная индуктивность между фазами d и q ротора.
Слайд 11 В более компактной форме уравнения (1.6) могут быть записаны:
(1.7)
При работе ЭМ

взаимные индуктивности обмоток статора и ротора изменяются, поэтому собственные и взаимные индуктивности обмоток, в общем случае, являются функцией электрического угла поворота ротора
Слайд 12 При симметричной неявнополюсной ЭМ собственные индуктивности обмоток статора и ротора не зависят

от положения ротора:
а взаимные индуктивности между обмотками статора и ротора равны нулю:
т.к. математические оси этих обмоток сдвинуты в пространстве относительно друг друга на 900.
Слайд 13 Взаимные индуктивности обмоток статора и ротора проходят полный цикл изменения при повороте

ротора на электрический угол 3600, поэтому с учетом принятых на рис. 1.23 направлений токов и знака угла поворота ротора можно записать:
Слайд 15 Таким образом для неявнополюсной обобщенной машины уравнения электрического равновесия с учетом (1.6)

– (1.8):
(1.9)
Слайд 16 В более компактном виде уравнения (1.9):
(1.10)
Обобщенная машина образует единую электромеханическую связь:

механическое движение оказывает влияет на электрическую систему, а электрическое движение – на механическую систему. Влияние механического движения на электрическую систему автоматически включено в электрические уравнения движения в силу закона Фарадея в соответствии с которым
Слайд 17 Таким образом выражение содержит напряжения, обусловленные механическим движением.
Влияние электрического движения на механическое

выражается в уравнении электромагнитного момента.
Выражение электромагнитного момента можно получить на основе принципа возможных перемещений и закона сохранения энергии.
Слайд 18 Если валу ЭД сообщено произвольное перемещение за время dt , то на

основе закона сохранения энергии:
Или сообщенная механическая энергия + сообщенная электрическая энергия = изменения в сообщенной механической энергии + изменения в сообщенной электрической энергии + потери
Слайд 19 После соответствующих преобразований последнего выражения уравнение электромагнитного момента:
(1.11)

Слайд 20 Преобразовав выражение (1.11) с помощью выражения (1.7)
(1.12)

Слайд 21 Таким образом уравнения (1.11) и (1.12) полностью характеризуют обобщенный вращающийся электромеханический преобразователь

энергии относительно его четырех пар электрических зажимов и пары механических зажимов:
(1.13)
Слайд 22 Эти уравнения, записанные через действительные переменные двухфазной модели, представляют собой развернутое математическое

описание динамического процесса электромеханического преобразования энергии, которое может быть конкретизировано для различных ЭД: АД, СМ, ДПТ, МДП и т.д.
Слайд 23 Уравнения (1.13) образуют систему из 5 уравнений, устанавливающую взаимосвязь между процессами в

механической и электрической частями ЭМС. Проявление такой взаимосвязи называется в теории ЭП – электромеханической связью.
Слайд 24 Выполнив дифференцирование первого уравнения системы (1.13):

Слайд 25 Рассмотрим все слагаемые последнего выражения.
Riii - представляет собой падение напряжение на активном

сопротивлении данной цепи,
результирующая ЭДС
самоиндукции и взаимной индукции, вызванные изменением токов в обмотках,
Слайд 26
- отражает взаимодействие механической и электрической частей ЭМ, т.к. представляет собой

результирующую ЭДС ei , наведенную в обмотке в результате механического движения ротора ЭМ.
Слайд 271.9. Параметры ЭМ
Параметры ЭМ – это коэффициенты перед независимыми переменными в уравнениях,

описывающих электромеханическое преобразование энергии.
Обычно независимые переменные – это токи.
Уравнения могут быть как дифференциальные, так и комплексными и алгебраическими.
(Самостоятельно)











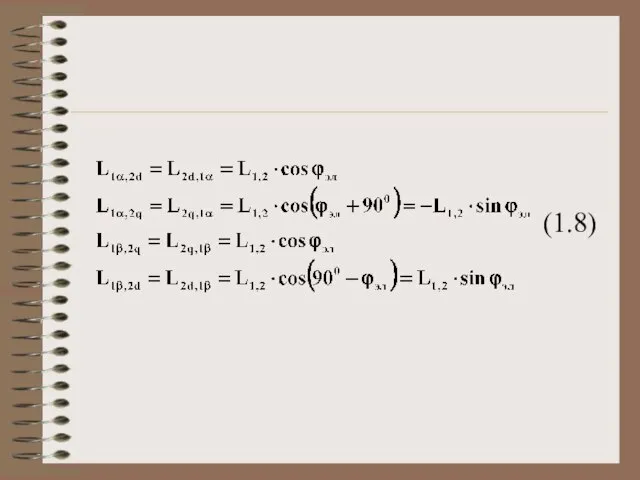













 Центр образования,исследований и разработок «ИНО Томск’2020»
Центр образования,исследований и разработок «ИНО Томск’2020» London's architectural ensembles of the XI-XX centuries as the fixed music
London's architectural ensembles of the XI-XX centuries as the fixed music На зарядку становись!
На зарядку становись! Планы на счастье. Ведущая тренинга
Планы на счастье. Ведущая тренинга Культура и быт народов Северного Кавказа
Культура и быт народов Северного Кавказа Как слово наше отзовется
Как слово наше отзовется ПРИРОДНЫЕ ГЕПАТОПРОТЕКТОРЫ
ПРИРОДНЫЕ ГЕПАТОПРОТЕКТОРЫ g?c суперфрукт Содержит липокаротины tm
g?c суперфрукт Содержит липокаротины tm Стекло
Стекло Историческое культурное наследие Белгородской области в 19 веке
Историческое культурное наследие Белгородской области в 19 веке Презентация на тему Строение электронных оболочек атомов
Презентация на тему Строение электронных оболочек атомов Этнокультурные особенности Германии
Этнокультурные особенности Германии Викторина. Году театра посвящается. Г. Сыктывкар
Викторина. Году театра посвящается. Г. Сыктывкар ВЕГЕТАТИВНЫЕ ОРГАНЫ РАСТЕНИЙ
ВЕГЕТАТИВНЫЕ ОРГАНЫ РАСТЕНИЙ Проверка домашнего задания
Проверка домашнего задания Межрегиональный фестиваль чувашской эстрадной песни Виръял Шевлисем, 25 летие
Межрегиональный фестиваль чувашской эстрадной песни Виръял Шевлисем, 25 летие A day in London
A day in London Приоритетный национальный проект «Образование» в нашей школе
Приоритетный национальный проект «Образование» в нашей школе ИНФОРМАЦИОННО-ТЕХНИЧЕСКОЕ УСТРОЙСТВО – СИСТЕМА МОВС-1-АФИ ГНУ АФИ РОССЕЛЬХОЗАКАДЕМИИ Система МОВС-1-АФИ – малогабаритная оптимиз
ИНФОРМАЦИОННО-ТЕХНИЧЕСКОЕ УСТРОЙСТВО – СИСТЕМА МОВС-1-АФИ ГНУ АФИ РОССЕЛЬХОЗАКАДЕМИИ Система МОВС-1-АФИ – малогабаритная оптимиз Використання МОБІЛЬНИХ ЗАСТОСУНКІВ ДЛЯ РЕЄСТРАЦІЇ ПОКАЗНИКІВ ФІЗИЧНОГО СТАНУ Кардаш
Використання МОБІЛЬНИХ ЗАСТОСУНКІВ ДЛЯ РЕЄСТРАЦІЇ ПОКАЗНИКІВ ФІЗИЧНОГО СТАНУ Кардаш Умножение и деление чисел (2 класс)
Умножение и деление чисел (2 класс) Курс семинаров. Интернет-маркетинг. Старт
Курс семинаров. Интернет-маркетинг. Старт Всемирный фестиваль молодёжи и студентов 2017
Всемирный фестиваль молодёжи и студентов 2017 пороки разв уха детей
пороки разв уха детей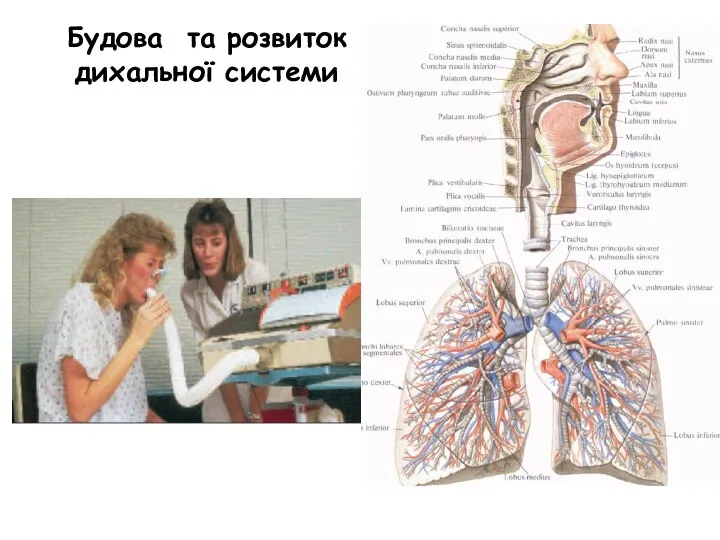 № 1-2-2 Будова та розвиток дихальної системи
№ 1-2-2 Будова та розвиток дихальної системи Общаться с ребенком. Как?
Общаться с ребенком. Как? Трансформация природной формы в дизайн-форму
Трансформация природной формы в дизайн-форму Моё хобби - ГЕОГРАФИЯ
Моё хобби - ГЕОГРАФИЯ