Содержание
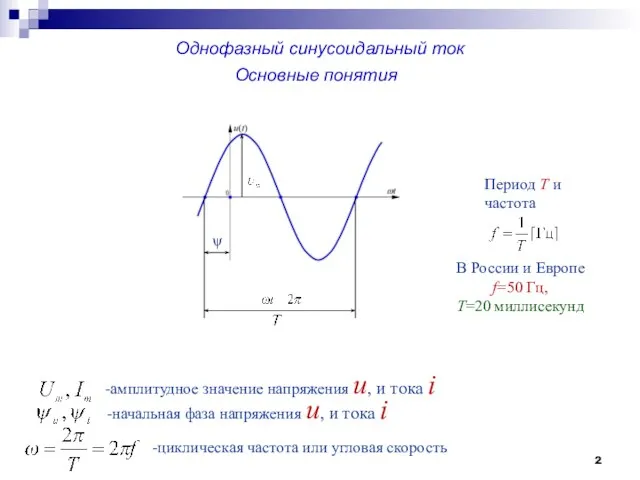
- 2. Однофазный синусоидальный ток Основные понятия ψ Период Т и частота В России и Европе f=50 Гц,
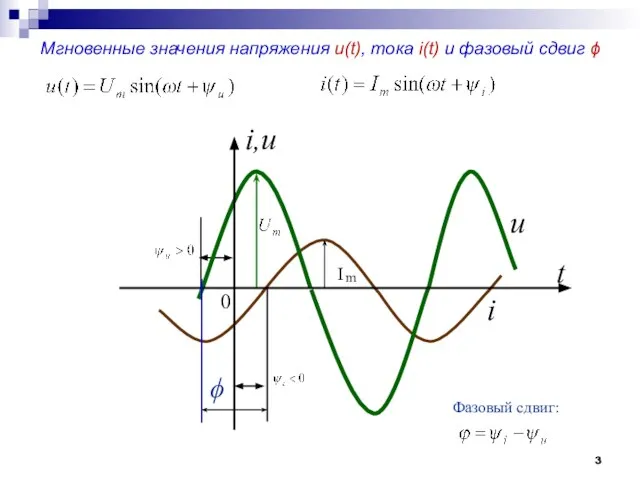
- 3. u i t i,u 0 Фазовый сдвиг: ϕ Мгновенные значения напряжения u(t), тока i(t) и фазовый
- 4. Средние и действующие значения величин Среднее значение переменной величины за период Т равно нулю. Поэтому среднее
- 5. Действующее значение переменной величины Работу, совершаемую при приложении напряжения на резистор с сопротивлением r находим по
- 6. Мощность в сети переменного тока Мощность отбирается от сети и совершает полезную работу Активная мощность. Единица
- 7. Соотношение действующих значений напряжения и тока и сдвиг по фазе в цепи синусоидального переменного тока Для
- 8. Реактивное напряжение: Полное напряжение: Введем величину: Тогда можем написать: где: Отсюда получим: Мгновенное значение напряжения на
- 9. введённые выше величины xL, xC, x, z имеют размерность сопротивления (Ом). Поэтому в соответствии с их
- 11. Скачать презентацию






 Юные свидетели оккупационного режима
Юные свидетели оккупационного режима Презентация на тему Рыцарство и его культура
Презентация на тему Рыцарство и его культура  Логика
Логика Тригонометрические уравнения
Тригонометрические уравнения Динамика процентных выплат
Динамика процентных выплат Британские праздники
Британские праздники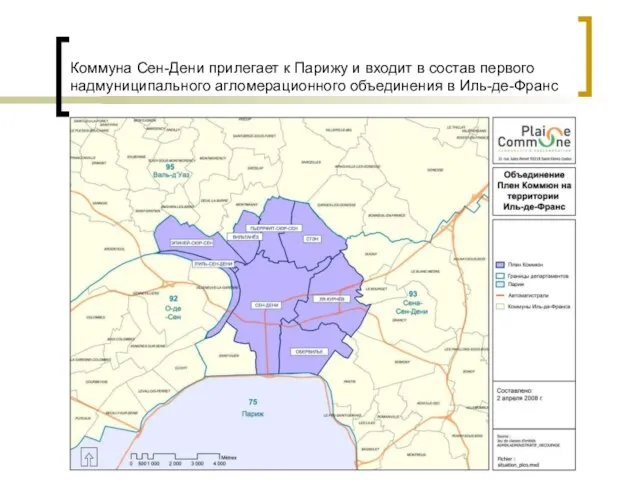 Коммуна Сен-Дени прилегает к Парижу и входит в состав первого надмуниципального агломерационного объединения в Иль-де-Франс
Коммуна Сен-Дени прилегает к Парижу и входит в состав первого надмуниципального агломерационного объединения в Иль-де-Франс Лекция 4. Интроспекция
Лекция 4. Интроспекция Видообразование
Видообразование Муж и жена - одна душа. 3 класс
Муж и жена - одна душа. 3 класс День Матери
День Матери Белорусский Государственный Университет
Белорусский Государственный Университет Культура малой Родины
Культура малой Родины 01.2022
01.2022 Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры
Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры Арктика в современном мире. Конструкция и материалы для построения жилых домов в Арктике
Арктика в современном мире. Конструкция и материалы для построения жилых домов в Арктике Возраст в произведениях художников
Возраст в произведениях художников “Чимээ анирг?йхэн туулай”
“Чимээ анирг?йхэн туулай” Теорема косинусов
Теорема косинусов Риторика. Ошибки, касающиеся аргументов
Риторика. Ошибки, касающиеся аргументов Презентация на тему Зимние забавы на Руси
Презентация на тему Зимние забавы на Руси  Аксиомы стереометрии
Аксиомы стереометрии «1С:Предприятие 8. Управление строительной организацией»
«1С:Предприятие 8. Управление строительной организацией» Свет в фотографии. Часть 1
Свет в фотографии. Часть 1 Параллелепипед (9 класс)
Параллелепипед (9 класс) Презентация на тему Культура и искусство в20 веке
Презентация на тему Культура и искусство в20 веке Правописание личных окончаний глаголов и суффиксов причастий
Правописание личных окончаний глаголов и суффиксов причастий Обеспечение информационной безопасности в автоматизированной системе учета населения города Нижнего Новгорода
Обеспечение информационной безопасности в автоматизированной системе учета населения города Нижнего Новгорода