Элементы математической статистики, комбинаторики и теории вероятностей. Сочетания и размещения. Часть I

Содержание
Введение
Пример 1. Учительница подготовила к контрольной работе…
Решения: 1.а)Решения: 1.а) 1.б)Решения: 1.а) 1.б) 1.в)Решения: 1.а) 1.б) 1.в) 1.г)
Пример 2. Известно, что х = 2аЗb5с с и а, Ь, с — числа из множества {0,1,2, 3}.
Решения: 2.а) Решения: 2.а) 2.б)Решения: 2.а) 2.б) 2.в)Решения: 2.а) 2.б) 2.в) 2.г)
Актуализация опорных знаний:
Определение 1Определение 1. n!
Теорема 1 о числе перестановок Теорема 1 о числе перестановок Pn =n!
Пример Пример 3Пример 3. К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
Решения: 3.а)Решения: 3.а) 3.б)Решения: 3.а) 3.б) 3.в)Решения: 3.а) 3.б) 3.в) 3. г)
Пример 4. В чемпионате по футболу участвовало 7 команд.
Решения: 1 способРешения: 1 способ; 2 способРешения: 1 способ; 2 способ; 3 способ
Анализ примера 4
Определение 2. Число сочетаний из n элементов по 2
Пример 5. Встретились 11 футболистов и 6 хоккеистов и каждый стал по одному разу играть с каждым в шашки
Теорема 3 и определение 3. Число размещений из n элементов по 2
Пример 6. В классе 27 учеников. К доске нужно вызвать двоих.
Итоги выборов двух элементов из Итоги выборов двух элементов из n Итоги выборов двух элементов из n данных
Источники
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Введение
Правило умножения, которое мы использовали в предыдущем параграфе, применимо не только к двум, но и к трём, четырём и т.д. испытаниям.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1
Учительница подготовила к контрольной работе 4 примера на решение линейных неравенств, 5 текстовых задач (две на движение и три на работу) и 6 примеров на решение квадратных уравнений (в двух из них D<0). В контрольной должно быть по одному на каждую из трех тем. Найти общее число:
а) всех возможных вариантов контрольной;
б)тех возможных вариантов, в которых встретится задача на движение;
в)тех возможных вариантов, в которых у квадратного уравнения будут корни;
г)тех возможных вариантов, в которых не встретятся одновременно задача на работу и квадратное уравнение, не имеющее корней.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1.а)
Подготовлены к к.р. 4 неравенств, 5 задач (2на движение и 3 на работу) и 6 квадратных уравнений (в 2 из них D<0, а в 4 D≥0). В к.р. по одному на каждую из трех тем.
Найти общее число:
а) всех возможных вариантов контрольной;
РЕШЕНИЕ:
а)При выборе неравенства есть 4 исхода,
при выборе задачи есть 5 исходов, при выборе квадратного уравнения есть 6 исходов. По правилу умножения получаем, что число всех вариантов контрольной работы равно 4 • 5 • 6 = 120.
ОТВЕТ: 120
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1.б)
Подготовлены к к.р. 4 неравенств, 5 задач (2на движение и 3 на работу) и 6 квадратных уравнений (в 2 из них D<0, а в 4 D≥0). В к.р. по одному на каждую из трех тем.
Найти общее число:
б)тех возможных вариантов, в которых встретится задача на движение;
РЕШЕНИЕ:
б) В предыдущем рассуждении меняется число исходов при выборе текстовой задачи: их всего два. Значит, можно составить 4•2•6=48 вариантов такой контрольной работы.
ОТВЕТ: 48
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1.в)
Подготовлены к к.р. 4 неравенств, 5 задач (2на движение и 3 на работу) и 6 квадратных уравнений (в 2 из них D<0, а в 4 D≥0). В к.р. по одному на каждую из трех тем.
Найти общее число:
в) тех возможных вариантов, в которых у квадратного уравнения будут корни;
РЕШЕНИЕ:
в) По сравнению с пунктом а) меняется число исходов при выборе уравнения: только в четырех случаях корни есть. Значит, можно составить 4•5•4=80 вариантов такой контрольной работы.
ОТВЕТ: 80
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1.г)
Подготовлены к к.р. 4 неравенств, 5 задач (2на движение и 3 на работу) и 6 квадратных уравнений (в 2 из них D<0, а в 4 D≥0). В к.р. по одному на каждую из трех тем.
Найти общее число: г)тех возможных вариантов, в которых не встретятся одновременно задача на работу и квадратное уравнение, не имеющее корней.
РЕШЕНИЕ: г) Из общего числа вариантов (120) мы вычтем те варианты, в которых встретятся одновременно и задача на работу, и квадратное уравнение, не имеющее корней. По сравнению с пунктом а) для них меняется число исходов при выборе текстовой задачи (3 варианта) и число исходов при выборе уравнения (только в 2 случаях корней нет). Значит, можно составить 4•3•2=24 варианта такой контрольной, работы, а условию задачи удовлетворяют остальные 120-24=96 вариантов.
Ответ: а) 120; б) 48; в) 80; г) 96.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 1.г)
Подготовлены к к.р. 4 неравенств, 5 задач (2на движение и 3 на работу) и 6 квадратных уравнений (в 2 из них D<0, а в 4 D≥0). В к.р. по одному на каждую из трех тем.
Найти общее число: г)тех возможных вариантов, в которых не встретятся одновременно задача на работу и квадратное уравнение, не имеющее корней.
РЕШЕНИЕ: г) Из общего числа вариантов (120) мы вычтем те варианты, в которых встретятся одновременно и задача на работу, и квадратное уравнение, не имеющее корней. По сравнению с пунктом а) для них меняется число исходов при выборе текстовой задачи (3 варианта) и число исходов при выборе уравнения (только в 2 случаях корней нет). Значит, можно составить 4•3•2=24 варианта такой контрольной, работы, а условию задачи удовлетворяют остальные 120-24=96 вариантов.
Ответ: а) 120; б) 48; в) 80; г) 96.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 2
Известно, что х = 2аЗb5с и а, Ь, с — числа из множества {0,1,2, 3}.
а)Найти наименьшее и наибольшее значения числа х.
б)Сколько всего таких чисел можно составить?
в)Сколько среди них будет четных чисел?
г)Сколько среди них будет чисел, оканчивающихся нулем?
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 2.а)
Известно, что х = 2аЗb5с и а, Ь, с — числа из множества {0,1,2, 3}.
а) Найти наименьшее и наибольшее значения числа х.
б) Сколько всего таких чисел можно составить?
в) Сколько среди них будет четных чисел?
г) Сколько среди них будет чисел, оканчивающихся нулем?
РЕШЕНИЕ :
а) хнаим = 203050 = 1, когда а=Ь=с=0.
хнаиб = 233353=8•27•125=27000, когда а=Ь=с=3.
Ответ: а) 1 и 27 000.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 2.б)
Известно, что х = 2аЗb5с и а, Ь, с — числа из множества {0,1,2, 3}.
а) Найти наименьшее и наибольшее значения числа х.
б) Сколько всего таких чисел можно составить?
в) Сколько среди них будет четных чисел?
г) Сколько среди них будет чисел, оканчивающихся нулем?
РЕШЕНИЕ : б) Рассмотрим три испытания: выбор числа а , выбор числа Ь и выбор числа с. Они независимы друг от друга, и в каждом имеется по четыре исхода. По правилу умножения получаем, что всего возможны 4•4•4=64 варианта. Ответ: б) 64.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 2.в)
Известно, что х = 2аЗb5с и а, Ь, с — числа из множества {0,1,2, 3}.
а) Найти наименьшее и наибольшее значения числа х.
б) Сколько всего таких чисел можно составить?
в) Сколько среди них будет четных чисел?
г) Сколько среди них будет чисел, оканчивающихся нулем?
РЕШЕНИЕ :
в) Число х = 2аЗb5с будет четным только в тех случаях, когда а > 0, т. е. когда аЄ{1,2,3}. Значит, для выбора числа а есть три исхода. Снова применим правило умножения. Получим 4•3•4 = 48 вариантов.
Ответ: в) 48
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 2.г)
Известно, что х = 2аЗb5с и а, Ь, с — числа из множества {0,1,2, 3}.
а) Найти наименьшее и наибольшее значения числа х.
б) Сколько всего таких чисел можно составить?
в) Сколько среди них будет четных чисел?
г) Сколько среди них будет чисел, оканчивающихся 0?
РЕШЕНИЕ : г) Число х = 2аЗb5с будет оканчиваться нулем только в тех случаях, когда среди множителей есть хотя бы одна двойка и есть хотя бы одна пятерка, т. е. когда аЄ{1,2,3} и cЄ{1,2,3}. Значит, для выбора чисел а и с есть по три исхода. Снова применим правило умножения. Получим 3•4•3=36 вариантов. Ответ: а) 1 и 27 000; б) 64; в) 48; г) 36.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Актуализация опорных знаний
В курсе алгебры 9 класса вы познакомились с понятием факториала и теоремой о перестановках. Напомним их.
Определение 1. Произведение подряд идущих первых n натуральных чисел n! и называют «эн факториал»:
n!=1·2·3·…·(n-2)·(n-1)·n
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Актуализация опорных знаний
Теорема 1. n различных элементов можно расставить по одному на n различных место ровно n! способами.
Как правило, эту теорему записывают в виде краткой формулы: Pn=n!
Pn-это число перестановок из n различных из n различных элементов, оно равно n!.
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Пример 3
К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
а) Сколькими способами можно рассадить гостей за столом?
б) Сколькими способами можно рассадить гостей за столом, если место хозяина дома уже известно?
в) Сколькими способами можно рассадить гостей за столом, если известно, что гостя С следует посадить рядом
с гостем А?
г) Сколькими способами можно рассадить гостей за столом, если известно, что гостя А не следует сажать рядом с гостем D?
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 3.а)
К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
а) Сколькими способами можно рассадить гостей за столом?
РЕШЕНИЕ: а) На 5 стульев должны сесть 5 человек (включая хозяина дома). Значит, всего имеется Р5 способов их рассаживания: Р5 = 5! = 120.
Ответ: 120
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 3.б)
К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
б) Сколькими способами можно рассадить гостей за столом, если место хозяина дома уже известно?
РЕШЕНИЕ:
б) Так как место хозяина фиксировано, то следует рассадить четырех гостей на четыре места. Это можно сделать Р4=4!=24 способами.
Ответ: 24
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 3.в)
К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
в) Сколькими способами можно рассадить гостей за столом, если известно, что гостя С следует посадить рядом
с гостем А?
РЕШЕНИЕ:
в) Сначала выберем место для гостя А. Возможны 5 вариантов. Если место гостя А уже известно, то гостя С следует посадить или справа, или слева от А, всего 2 варианта. После того как места для А и С уже выбраны, нужно трех человек произвольно рассадить на 3 оставшихся места: Р3 = 3! = 6 вариантов. Остается применить правило умножения: 5 • 2 • 6 = 60. Ответ: 60
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 3.г)
К хозяину дома пришли гости А, Б, С, D. За круглым столом — пять разных стульев.
г) Сколькими способами можно рассадить гостей за столом, если известно, что гостя А не следует сажать рядом с гостем D?
РЕШЕНИЕ г) Решение такое же, как и в пункте в). Место для гостя D после выбора места для А можно также выбрать двумя способами: на два отдаленных от А стула.
Ответ: а) 120; б) 24; в) 60; г) 60.
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Пример 4.
В чемпионате по футболу участвовало 7 команд. Каждая команда сыграла по одной игре с каждой командой. Сколько всего было игр?
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

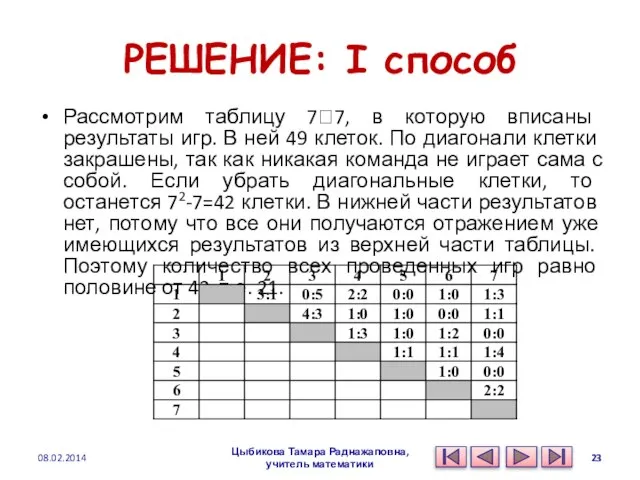
РЕШЕНИЕ: I способ
Рассмотрим таблицу 7?7, в которую вписаны результаты игр. В ней 49 клеток. По диагонали клетки закрашены, так как никакая команда не играет сама с собой. Если убрать диагональные клетки, то останется 72-7=42 клетки. В нижней части результатов нет, потому что все они получаются отражением уже имеющихся результатов из верхней части таблицы. Поэтому количество всех проведенных игр равно половине от 42, т.е. 21.
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

РЕШЕНИЕ: II способ
Произвольно пронумеруем команды №1, №2, …, №7 и посчитаем число игр поочередно. Команда №1 встречается с командами №2-7 – это 6 игр, №2 – с №3-7 – это 5 игр и т.д. Всего 6+5+4+3+2+1=21 игр.
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

РЕШЕНИЕ: III способ
Используем геометрическую модель: 7 команд – это вершины выпуклого 7-угольника, а отрезок между двумя вершинами – это встреча двух соответствующих команд: сколько отрезков – столько игр. Из каждой вершины выходит 6 отрезков – столько игр. Получается 7·6=42 отрезков, каждый из которых посчитан дважды: и как АВ, и как ВА. Значит, 42/2=21 отрезок.
ОТВЕТ: 21
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Анализ примера 4
Состав игры определен, как только мы выбираем две команды. Значит, количество всех игр в турнире для n команд – это в точности количество всех выборов двух элементов из n данных элементов. Важно при этом то, что порядок выбора не имеет значения, т.е. если выбрано две команды, то какая из них первая, а какая вторая – не существенно.
Первую команду можно выбрать n способами, а вторую – (n-1) способами. По правилу умножения получаем n(n-1). Но при этом состав каждой игры посчитан дважды. Значит, число игр равно n(n-1)/2. Тем самым фактически доказана следующая теорема.
Теорема 2 (о выборе двух элементов). Если множество состоит из n элементов и требуется выбрать два элемента без учета их порядка, то такой выбор можно произвести n(n-1)/2 способами.
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Определение 2
Достаточно длинный словесный оборот «число всех выборов двух элементов без учета их порядка из n данных» неудобен при постоянном использовании в решении задач. Математики поступили просто: ввели новый термин и специальное обозначение.
Определение 2. число всех выборов двух элементов без учета их порядка из n данных элементов называют числом сочетаний из n элементов по 2 и обозначают (цэ из эн по два).
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Пример 5.
Встретились 11 футболистов и 6 хоккеистов и каждый стал по одному разу играть с каждым в шашки, которые они «давненько не брали в руки». Сколько встреч было:
а)между футболистами;
б)между хоккеистами;
в)между футболистами и хоккеистами;
г)всего?
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

РЕШЕНИЕ:
а)
б)
в) Будем действовать по правилу умножения. Одно испытание – выбор футболиста, а другое испытание – выбор хоккеиста. Испытания предполагаются независимыми, и у них соответственно 11 и 6 исходов. Значит получится 11·6=66 игр.
г) Можно сложить все предыдущие ответы: 55+15+66=136; но можно использовать и формулу для числа сочетаний:
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Теорема 3 и определение 3
А что получится, если мы будем учитывать порядок двух выбираемых элементов? По правилу умножения получаем следующую теорему.
Теорема 3. Если множество состоит из n элементов и требуется выбрать из них два элемента, учитывая их порядок, то такой выбор можно произвести n(n-1) способами.
Доказательство: Первый по порядку элемент можно выбрать n способами. Из оставшихся (n-1) элементов второй по порядку элемент можно выбрать (n-1) способом. Так как два этих испытания (выбора) независимы друг от друга, то по правилу умножения получаем n(n-1).
Определение 3. Число всех выборов двух элементов с учетом их порядка из n данных называют числом размещений из n элементов по 2 и обозначают
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики

Пример 6
В классе 27 учеников. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если:
а) первый ученик должен решить задачу по алгебре, а второй — по геометрии;
б) они должны быстро стереть с доски?
Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Цыбикова Тамара Раднажаповна, учитель математики
08.02.2014

Итоги выборов двух элементов
А как будут выглядеть формулы, если в них верхний индекс 2 заменить на 3, 4, … и вообще на произвольное число k, 1≤k ≤n?
Здесь мы переходим к основному вопросу параграфа – к выборам, состоящим из произвольного числа элементов.
08.02.2014
Цыбикова Тамара Раднажаповна, учитель математики