Содержание
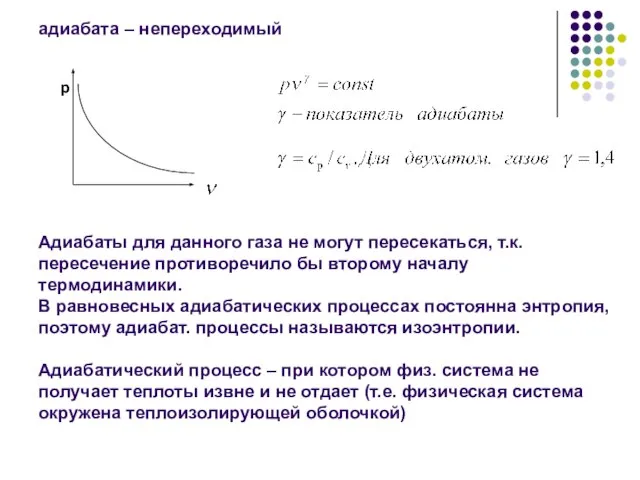
- 2. адиабата – непереходимый Адиабаты для данного газа не могут пересекаться, т.к. пересечение противоречило бы второму началу
- 3. Согласно первому началу термодинамики δQ=du+pdv, т.е. сообщаемое системе количество теплоты равно сумме приращений внутренней энергии du
- 4. Для необратимых (неравновесных) процессов интеграл от приведенной теплоты по замкнутому контуру всегда отрицателен . Энтропия адиабатически
- 5. Термодинамика – наука о наиболее общих свойствах макроскопических физических систем, находящихся в состоянии термодинамического равновесия и
- 6. Б) Статистическая физика связывает энтропию с вероятностью осуществления данного макроскопического состояния системы. Определяется через логарифм статистического
- 7. В уравнении состояния идеального газа постоянная Больцмана связывает энтропию физического состояния системы с ее термодинамической вероятностью
- 8. В отличие от термодинамики, статистическая физика рассматривает особый класс процессов – флуктуации, при которых система переходит
- 9. Энтропия в информатике
- 10. Определение entropia – (греч.) поворот, превращение В теории информации энтропия – количество случайности, мера хаотичности информации,
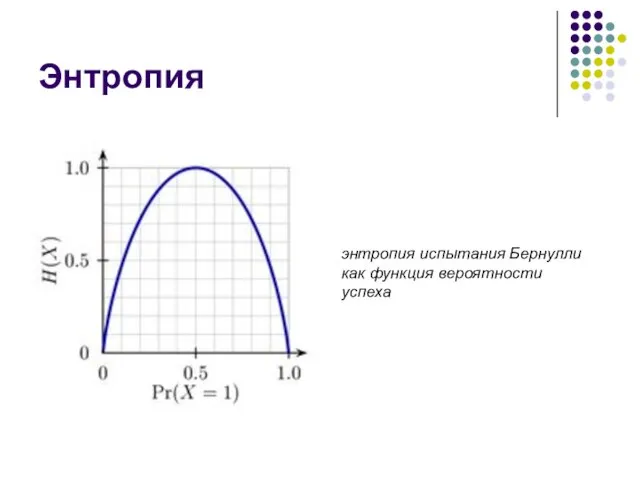
- 11. Энтропия энтропия испытания Бернулли как функция вероятности успеха
- 12. Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается
- 13. Определение энтропии сделано на основе следующих предположений: Мера должна быть непрерывной; т. е. изменение значения величины
- 14. Оценка энтропии текста (модель Маркова) Двоичная энтропия: Для Марковской модели первого порядка: Для Марковской модели второго
- 15. Вывод шенноновской энтропии , где – число возможных комбинаций исходов (событий), соответствующее данному распределению – число
- 17. Заменим Ax на px = Ax/P и P на 1
- 18. - уравнение Больцмана для энтропии в термодинамике Таким образом, энтропия по Шеннону является решением уравнения:
- 19. Понятие энтропии в статистической физике
- 20. Предмет статистической физики Статистическая физика - раздел физики, задача которого выразить свойства макроскопических тел, т. е.
- 21. Статистический подход Если в какой-то момент времени заданы координаты и скорости всех частиц тела и известен
- 22. Движение в фазовом пространстве Рассмотрим систему из N одинаковых взаимодействующих частиц, находящихся в конечном, но макроскопически
- 23. Движение в фазовом пространстве Траектория фазовой точки в фазовом пространстве называется фазовой траекторией. Для консервативных систем
- 24. Статистические ансамбли Статистический ансамбль - совокупность сколь угодно большого числа одинаковых физических систем многих частиц («копий»
- 25. Статистические ансамбли Статистический ансамбль задается функцией распределения ρ(p,q,t) dw = ρ(p, q, t)dpdq Условие нормировки: Минимальный
- 26. Микроканонический ансамбль Функция распределения ρ(p, q) ансамбля постоянна в слое фазового пространства между двумя изоэнергетическими поверхностями,
- 27. Статистический вес Константа Ω(E,N,V) называется статистическим весом и определяется из условия нормировки: Физический смысл - число
- 28. Энтропия Логарифм функции распределения с обратным знаком: Энтропия:
- 29. Статистический смысл энтропии Пусть макроскопическое состояние системы, кроме значений E, N, V характеризуется какими-либо параметрами x
- 31. Скачать презентацию











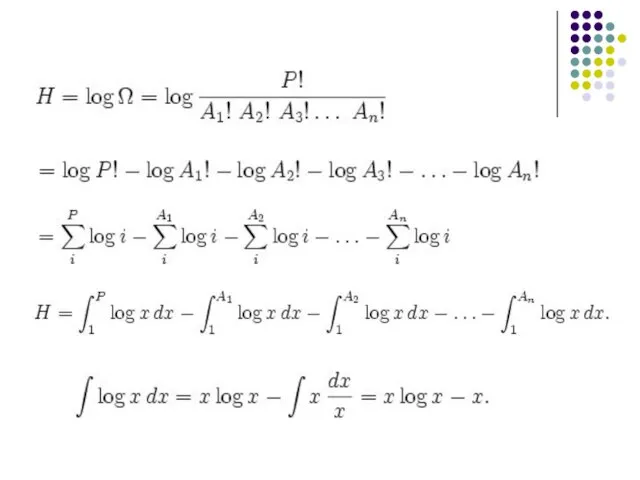












 В грозную пору 1812 года
В грозную пору 1812 года Презентация на тему Наречие
Презентация на тему Наречие  Услуги в сфере красоты. Бизнес-план
Услуги в сфере красоты. Бизнес-план Анализ воспитательной работы в школе
Анализ воспитательной работы в школе Материалы к Заседанию Комиссии при Президенте Российской Федерации по модернизации и технологическому развитию экономики Росси
Материалы к Заседанию Комиссии при Президенте Российской Федерации по модернизации и технологическому развитию экономики Росси Презентация на тему Борис Леонидович Пастернак (1890 – 1960 г.г.) Жизнь и творчество
Презентация на тему Борис Леонидович Пастернак (1890 – 1960 г.г.) Жизнь и творчество  Функциональный менеджмент: строительный комплекс. Программа повышения квалификации
Функциональный менеджмент: строительный комплекс. Программа повышения квалификации Презентация на тему Взаимодействие с родителями при формировании гендерной, семейной, гражданской принадлежности
Презентация на тему Взаимодействие с родителями при формировании гендерной, семейной, гражданской принадлежности Витраж
Витраж Презентация на тему Александр Сергеевич Грибоедов
Презентация на тему Александр Сергеевич Грибоедов МАЙСКИЙ ЧАЙРАЗРАБОТКА КОНЦЕПЦИИ POS-МАТЕРИАЛОВ
МАЙСКИЙ ЧАЙРАЗРАБОТКА КОНЦЕПЦИИ POS-МАТЕРИАЛОВ Устройство гранат
Устройство гранат Литературный вечер
Литературный вечер Формирование вероятностно-статистических моделей объектов эксплуатации летательных аппаратов
Формирование вероятностно-статистических моделей объектов эксплуатации летательных аппаратов Виды лыжных ходов
Виды лыжных ходов Творческая биография Е.Е. Лансере
Творческая биография Е.Е. Лансере Русский язык 2 класс( 4 четверть)
Русский язык 2 класс( 4 четверть) Constructions impersonnelles suivies du subjonctif
Constructions impersonnelles suivies du subjonctif Управление корпоративной социальной деятельностью Заместитель руководителя Департамента внешних коммуникаций ФК «УРАЛСИБ»
Управление корпоративной социальной деятельностью Заместитель руководителя Департамента внешних коммуникаций ФК «УРАЛСИБ»  Факультет туризма и гостеприимства
Факультет туризма и гостеприимства Історія виникнення бадмінтону
Історія виникнення бадмінтону Презентация на тему Школьник и курение
Презентация на тему Школьник и курение Второй закон Ньютона
Второй закон Ньютона Проводники и изоляторы
Проводники и изоляторы Организационно-правовое регулирование муниципальной службы в субъекте Российской Федерации
Организационно-правовое регулирование муниципальной службы в субъекте Российской Федерации Один день из жизни группы №8«Маленькая страна»
Один день из жизни группы №8«Маленькая страна» В мире северной фразеологии
В мире северной фразеологии Виды рекламы по рекламодателям
Виды рекламы по рекламодателям