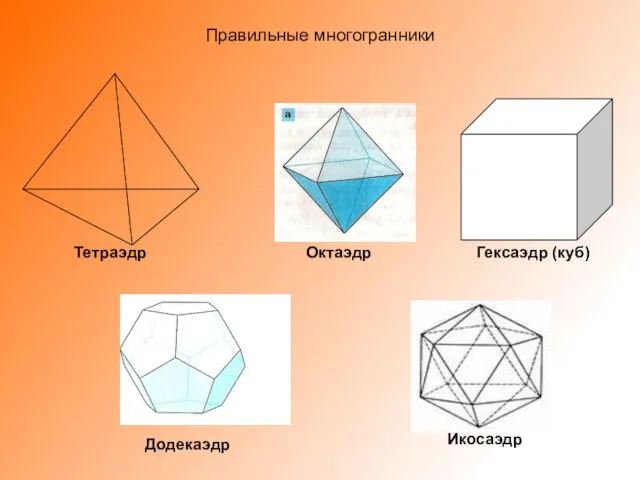
Слайд 3Правильные многогранники
Тетраэдр
Октаэдр
Гексаэдр (куб)
Икосаэдр
Додекаэдр
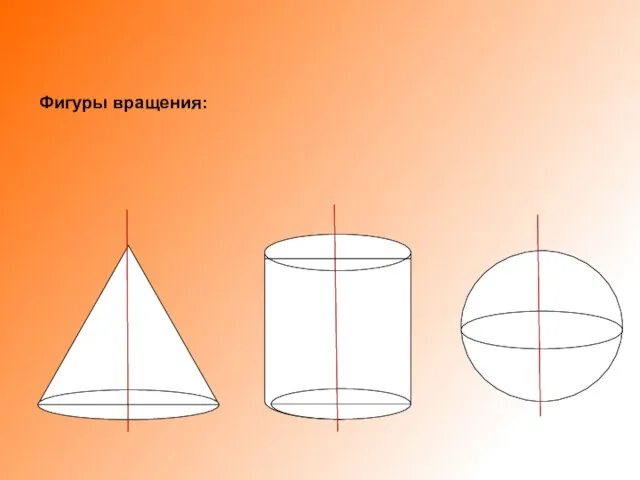
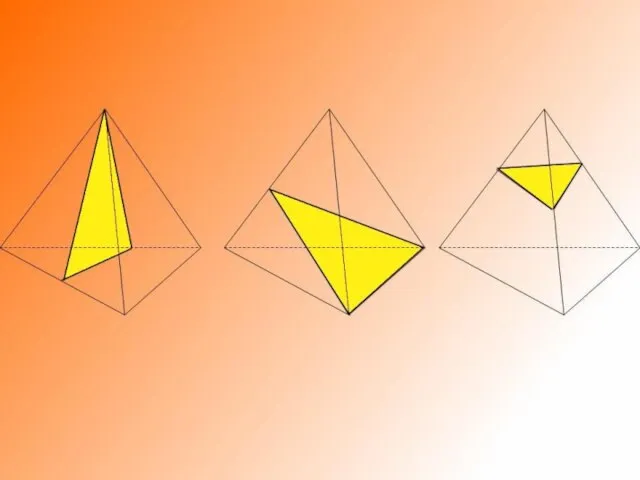
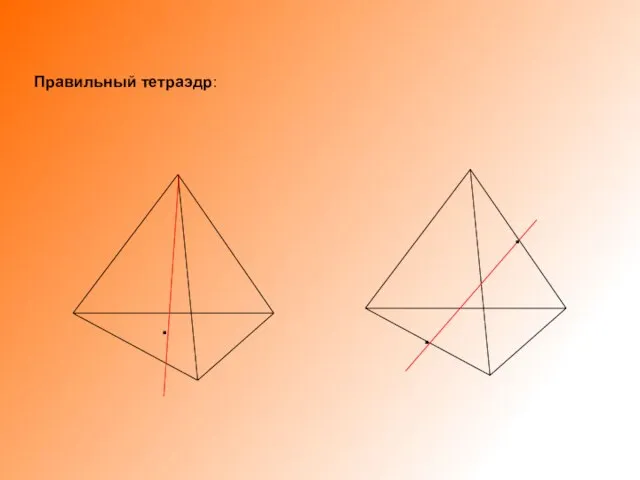
Слайд 5• при вращении тетраэдра в зависимости от оси вращения,
получается конус, два

разных конуса с общим основанием, однополостный
гиперболоид;
• при вращении куба: цилиндр, однополостный гиперболоид, система из
двух конусов и однополостного гиперболоида;
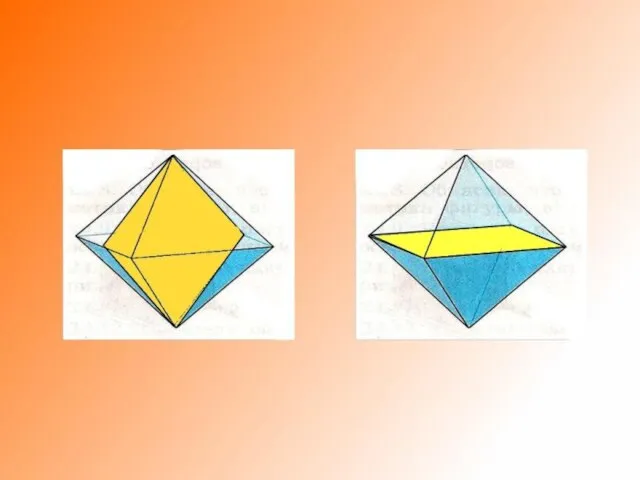
Слайд 6• при вращении октаэдра: два конуса с общим основанием, однополостный
гиперболоид, система

из двух цилиндров и двух однополостных гиперболоидов;
• при вращении икосаэдра: система из двух усеченных конусов и однополостного
гиперболоида, система из двух конусов и однополостного гиперболоида,
система из двух плоских кругов (сверху и снизу), трех гиперболоидов и системы
цилиндров;
Слайд 7• при вращении додекаэдра: совокупность системы однополостных
гиперболоидов вращения с однополостным гиперболоидом

и системой конусов,
система их двух усеченных конусов и однополостного гиперболоида,
система из четырех пар однополостных гиперболоидов и одной пары цилиндров.
Слайд 8Если прямая параллельна оси вращения, то получается
цилиндрическая поверхность.
Если прямая пересекает ось

вращения, то получается
коническая поверхность.
Если прямая скрещивается с осью вращения, то получается
однополостный гиперболоид вращения.
Слайд 9Однополостной гиперболоид:
Гиперболоид вращения может быть получен вращением прямой
вокруг другой прямой,

скрещивающейся с ней.
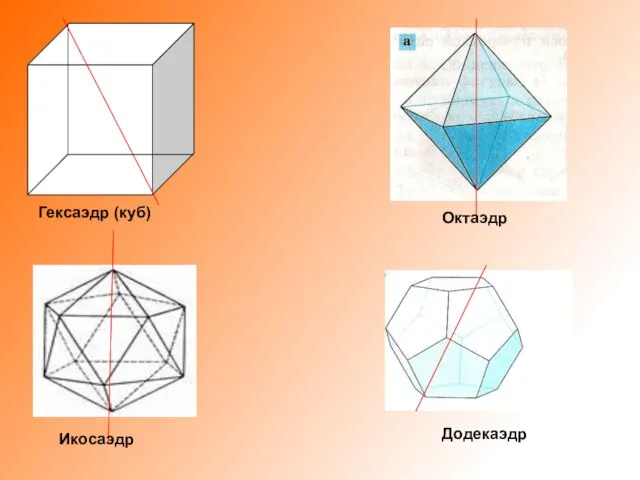
Слайд 14Додекаэдр
Икосаэдр
Октаэдр
Гексаэдр (куб)
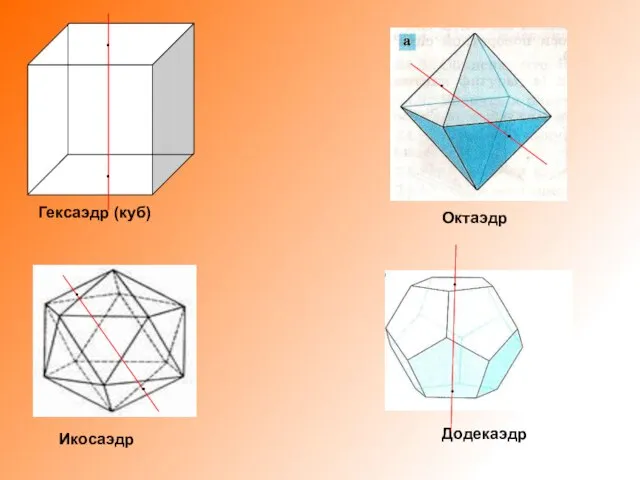
Слайд 15Додекаэдр
Икосаэдр
Октаэдр
Гексаэдр (куб)
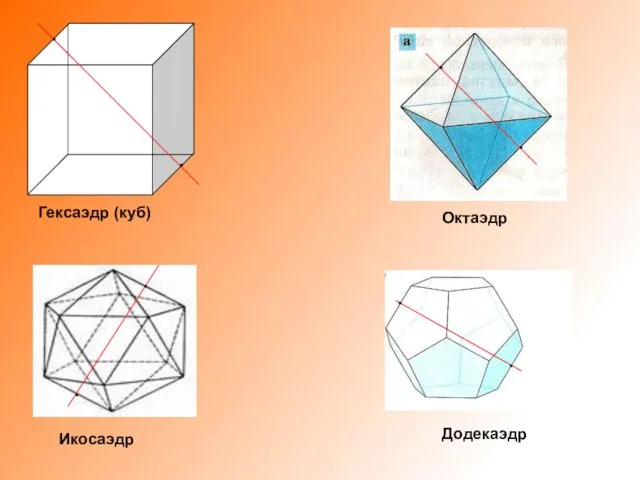
Слайд 16Додекаэдр
Икосаэдр
Октаэдр
Гексаэдр (куб)
Слайд 18 При вращении Платоновых тел, вращая разные
многогранники, можно получить одинаковые фигуры

вращения:
• при вращении тетраэдра и октаэдра фигурой вращения являются
однополостный гиперболоид а также два конуса с общим основанием;
• при вращении икосаэдра и додекаэдра – система из двух усеченных
конусов и однополостного гиперболоида;
• при вращении икосаэдра и куба - система из двух конусов и
однополостного гиперболоида.













 Карта текущего потока создания ценности
Карта текущего потока создания ценности Турнир Память 2018 год
Турнир Память 2018 год Презентация на тему Гидродинамические аварии
Презентация на тему Гидродинамические аварии Let’s talk about Weddings
Let’s talk about Weddings Ахмадиева Елена Федоровна, учитель русского языка и литературы
Ахмадиева Елена Федоровна, учитель русского языка и литературы ИнфоСофт: История и корпоративная культура компании
ИнфоСофт: История и корпоративная культура компании Презентация на тему "Формулы речевого этикета, этикетные слова, и стиль общения детей 9-11 лет" - скачать презентации по Педагог
Презентация на тему "Формулы речевого этикета, этикетные слова, и стиль общения детей 9-11 лет" - скачать презентации по Педагог А
А Завоевание турками-османами Балканского полуострова
Завоевание турками-османами Балканского полуострова Особенности земельного контроля в Республике Башкортостан
Особенности земельного контроля в Республике Башкортостан Проблемы прозы Чехова 1890-х годов
Проблемы прозы Чехова 1890-х годов Презентация на тему Ребусы по информатике
Презентация на тему Ребусы по информатике  Мотив одиночества в лирике М. Ю. Лермонтова
Мотив одиночества в лирике М. Ю. Лермонтова Матрешка
Матрешка ЛЕКЦИЯ 16.СТАРЕНИЕ – ЗАКОНОМЕРНЫЙ ЭТАП ОНТОГЕНЕЗА. ОСНОВНЫЕ ПРОЯВЛЕНИЯ и ЗАКОНОМЕРНОСТИ. ГИПОТЕЗЫ СТАРЕНИЯ.
ЛЕКЦИЯ 16.СТАРЕНИЕ – ЗАКОНОМЕРНЫЙ ЭТАП ОНТОГЕНЕЗА. ОСНОВНЫЕ ПРОЯВЛЕНИЯ и ЗАКОНОМЕРНОСТИ. ГИПОТЕЗЫ СТАРЕНИЯ. Презентация на тему Научное исследование
Презентация на тему Научное исследование  Устройство сборно-разборных деревянных покрытий
Устройство сборно-разборных деревянных покрытий Знатоки электричества. Викторина
Знатоки электричества. Викторина Alexander Graham Bell, an American engineer
Alexander Graham Bell, an American engineer Презентация на тему Решетников "Опять двойка"
Презентация на тему Решетников "Опять двойка" Презентация на тему Исследовательская и проектная деятельность в начальной школе
Презентация на тему Исследовательская и проектная деятельность в начальной школе Устройство глаза
Устройство глаза Профессиональные конкурсы как средство повышения педагогической компетентности учителя
Профессиональные конкурсы как средство повышения педагогической компетентности учителя Управление проектами
Управление проектами О Дружбе
О Дружбе Компьютерные вирусы
Компьютерные вирусы Звук и буква "Х"
Звук и буква "Х" Понятие информационной безопасности
Понятие информационной безопасности