Пифагор. Его жизнь и труды

Содержание:
Биография
1. Знаменитая Пифагорейская Y
2. Пифагорейская теория о переселении душ
3. Символические афоризмы Пифагора
Теорема Пифагора
Доказательства теоремы Пифагора
Заключение

Биография.
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Пифагор - это не имя, а прозвище, данное ему за то, что он высказывал истину так же постоянно, как дельфийский оракул (“Пи­фагор” значит “убеждающий речью”. Этимология связывает нарече­ние с культом Аполлона Пифийского). Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора).

Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.

На Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас. В результате первой же прочитанной лекции Пифагор приоб­рел 2000 учеников, которые не вернулись домой, а вместе со своими женами и детьми образовали громадную школу и создали государ­ство, названное «Великая Греция», в основу которого были положе­но законы и правила Пифагора, почитаемые как божественные за­поведи.

...Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.

Знаменитая Пифагорейская Y
Знаменитая пифагорейская Y означала силу выбора и использовалась в Мистериях, как эмблема Развилки Пути. Главная дорога разделялась на две – направо и налево. Правая ветвь была названа Божественной Мудростью, а левая Земной Мудростью.

Пифагорейская теория о переселении душ.
Пифагор учил: "во-первых, душа бессмертна, во-вторых, она переселяется в другие виды животных, в-третьих, все, что некогда произошло, через определенные периоды времени происходит снова, а нового нет абсолютно ничего и в четвертых, что все живые существа следует считать родственными друг другу". Говорят, что Пифагор, подобно святому Франциску, произносил перед животными проповеди.

Символические афоризмы Пифагора.
Афористические утверждения были одним из любимых методов Пифагора и широко использовались в пифагорейском университете в Протоне. Вот некоторые из них:
1. Отклоняйся от дорог исхоженных, используй нехоженые пути. Это надо понимать так, что тот, кто ищет мудрости, должен искать её в уединении.
2. Ласточек в доме не держи. т. е. не принимай гостей болт­ливых и не сдержанных на язык
3. Не протягивай охотно свою правую руку никому. Это надо понимать так, что следует иметь свой собственный ум и не делиться им с тем кому это не нужно.
4. Не садись на хлебную меру. т. е. не живи праздно.
5. Уходя, не оглядывайся. т. е. перед смертью не цепляйся за жизнь.
6.Помогай человеку в поднятии тяжести, но не помогай в сложении её. Следует учиться помогать старательным, но не помогать тем, кто стремится избежать ответственности.

Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
в с с = а + в
а

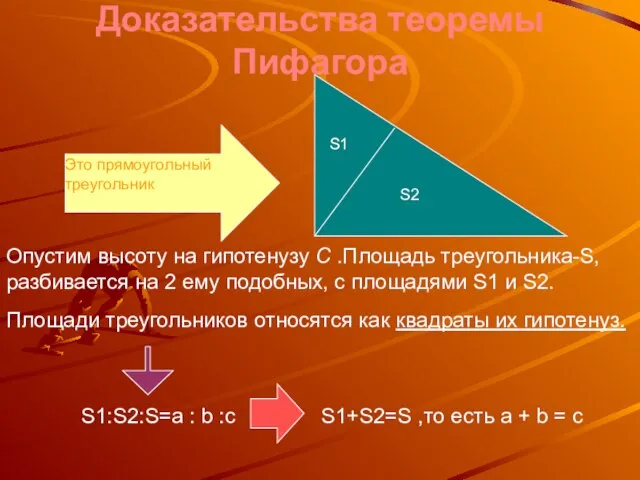
Доказательства теоремы Пифагора
Ч.т.д.
Это прямоугольный
треугольник
S1
S2
Опустим высоту на гипотенузу C .Площадь треугольника-S,
разбивается на 2 ему подобных, с площадями S1 и S2.
Площади треугольников относятся как квадраты их гипотенуз.
S1:S2:S=a : b :c
S1+S2=S ,то есть a + b = c

Алгебраический метод доказательства.
A
Q
Треугольники
А1, А2, А3,А4
равны
треугольнику А
(по двум катетам и
прямому углу)
Следовательно их гипотенузы равны
P
Четырехугольник Р является квадратом
(Все стороны равны,
углы прямые)

Равенство углов в четырехугольнике Р доказывается следующим образом:
Пусть а и b – величины острых углов треугольника
Тогда а + b = 900
Угол А + (а + b) = 1800
1800 – 900 = 900
Угол А равен 900
Аналогичным способом находятся градусные меры остальных углов квадрата Р.

Получим площадь квадрата Q
S(Q) = S(P) + 4S(T)
S(Q) = (а + b)2
S(P) = c2
S(T) = 1/2(ab)
(а + b)2 = c2 + 4(1/2(ab))
(а + b)2 = a 2 + 2ab + b 2
a 2+ 2ab + b 2 = c2 + 2ab
a 2 + b 2 = c2
Ч.т.д.

Доказательство.
Площадь данного прямоугольника с одной стороны равна 0.5ab, с другой 0.5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r=0.5(a+b-c)).
A
C
B
a
b
c
Имеем:
0.5ab=0.5pr=0.
5(a+b+c)*0.5
(a+b-c)
Отсюда следует, что с2= а2+b2
Что и требовалось доказать!