Раздел: Стереометрия

Начальные понятия стереометрии
Аксиомы и следствия из них

Вопросы к лекции.
1. Когда зародилась наука геометрия?
2. Что означает слово «геометрия»?
3. Какой ученый первым отразил геометрические понятия в своих сочинениях?
4. Как Вы понимаете, что такое аксиомы?
5. Что такое теоремы в Вашем понятии?
6. На какие разделы делится школьный курс геометрии?
7. Что изучает планиметрия?
8. Что изучает стереометрия?
9. Какие фигуры являются основными в пространстве, как они обозначаются?
10. Аксиомы планиметрии.
11. Аксиомы стереометрии.
12. Сформулируйте теоремы – следствия из аксиом стереометрии.

Евклид – древнегреческий математик

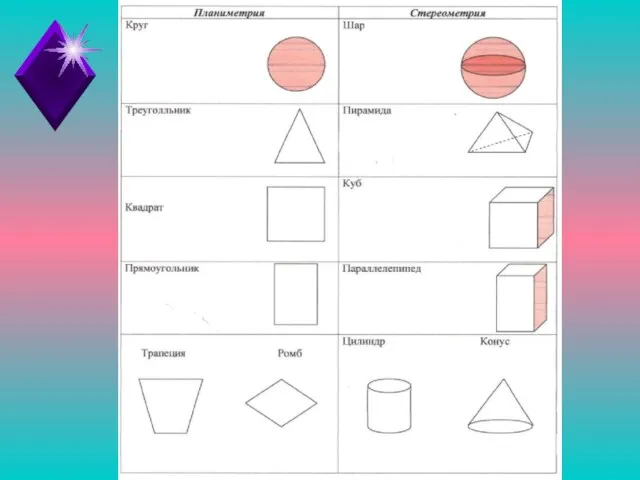
ГЕОМЕТРИЯ
Планиметрия
Стереометрия

Планиметрия - это раздел геометрии, который изучает фигуры на плоскости.
А стереометрия?
Подумай и сформулируй!

Это раздел геометрии, в котором изучаются фигуры, расположенные в пространстве.
Шар ?
?Пирамида
Куб?
Плоскость?
?Прямая

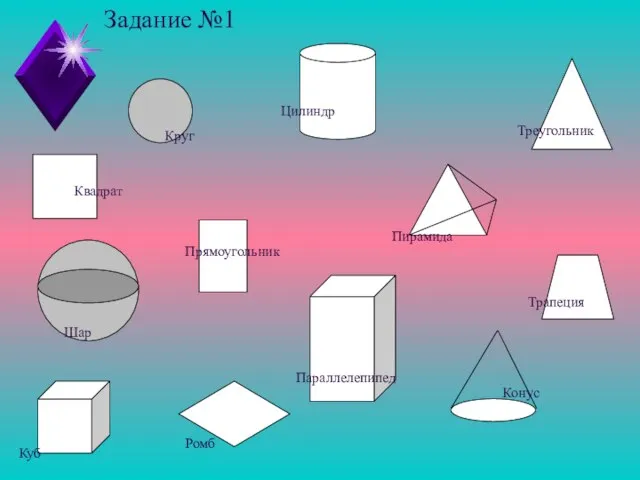
Задание №1
Цилиндр
Пирамида
Ромб
Конус
Прямоугольник
Треугольник
Шар
Трапеция
Параллелепипед
Квадрат
Куб
Круг

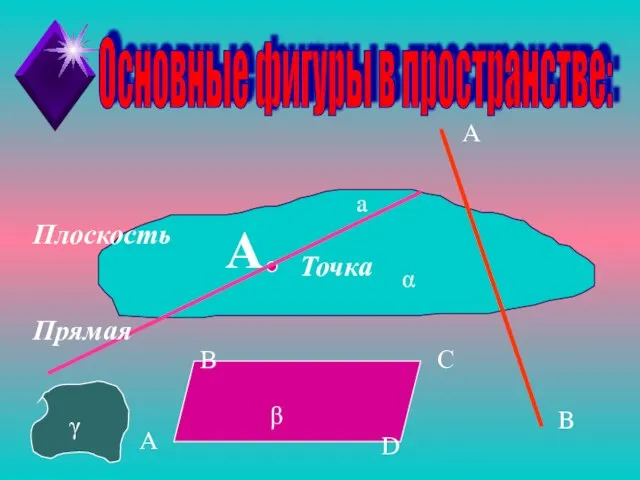
Плоскость
А
Точка
Прямая
a
A
B
Основные фигуры в пространстве:
α
β
А
В
С
D
γ

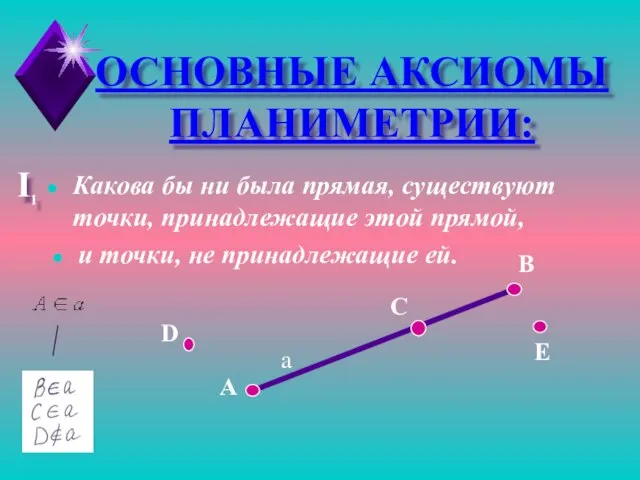
ОСНОВНЫЕ АКСИОМЫ ПЛАНИМЕТРИИ:
I1
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой,
А
B
С
и точки, не принадлежащие ей.
a

I2
Через любые две точки можно провести прямую, и только одну.
ОСНОВНЫЕ АКСИОМЫ ПЛАНИМЕТРИИ:

ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С1
Какова бы ни была плоскость, существуют точки, принадлежащие ей,
и точки, не принадлежащие ей:
α

ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С2
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку:
K

ОСНОВНЫЕ АКСИОМЫ СТЕРЕОМЕТРИИ:
С3
Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну:
S

Теорема 1.
Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

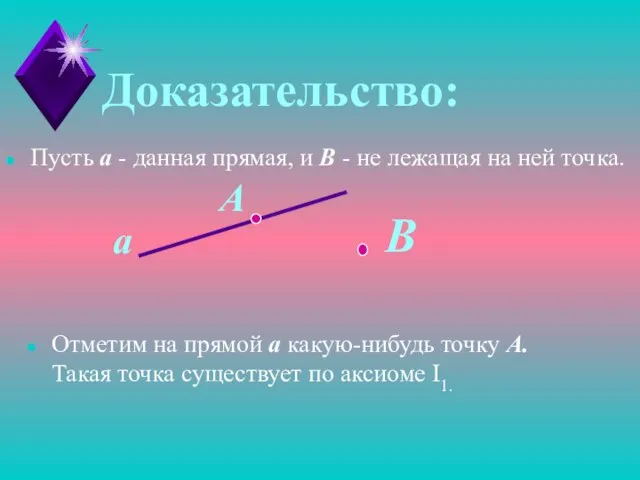
Доказательство:
Пусть а - данная прямая, и В - не лежащая на ней точка.
а
Отметим на прямой а какую-нибудь точку А. Такая точка существует по аксиоме I1.

Проведем через точки А и В прямую b (аксиома I2)
Доказательство:
b

Прямые а и b различны,
Доказательство:
а
b
так как точка B прямой b
не лежит на прямой а.
Прямые а и b имеют общую точку А.

Проведем через прямые а и b плоскость α (аксиома С3).
Доказательство:
Эта плоскость проходит через прямую а и точку B.

Докажем теперь, что плоскость α ,
Доказательство:
проходящая через прямую а
а
и точку B,
b
единственна .
Допустим, что существует другая, отличная от α , плоскость α1 проходящая через прямую а и точку B.

По аксиоме С2 плоскости α и α1 , будучи различными, пересекаются по прямой, а именно по прямой а .
Доказательство:
а
Следовательно, любая общая точка плоскостей α и α1 лежит на прямой а .
b

Но точка B ,
общая для плоскостей α и α1 , заведомо не лежит на прямой а . Получили противоречие. Теорема доказана.
а
Доказательство:

Теорема 2.
Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.

Теорема 3.
Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

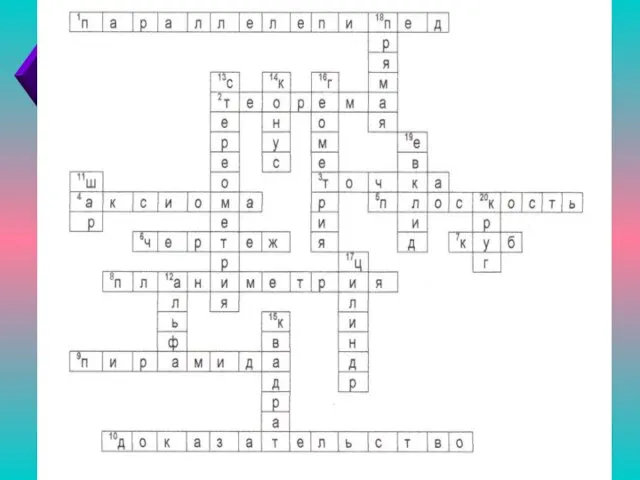
Задание №3
Задание №3

Задание № 4.
В пространстве задан куб.
Каким плоскостям (граням) принадлежит точка (вершина) А?
По какой прямой пересекаются плоскости AA1D1D и ABCD?

Итак, подведем итоги:
1. Когда зародилась наука геометрия?
2. Что означает слово «геометрия»?
3. Какой ученый первым отразил геометрические понятия в своих сочинениях?
4. Как Вы понимаете, что такое аксиомы?
5. Что такое теоремы в Вашем понятии?
6. На какие разделы делится школьный курс геометрии?
7. Что изучает планиметрия?
8. Что изучает стереометрия?
9. Какие фигуры являются основными в пространстве, как они обозначаются?
10. Аксиомы планиметрии.
11. Аксиомы стереометрии.
12. Сформулируйте теоремы – следствия из аксиом стереометрии.

Домашнее задание
Выучить опорный конспект.
Доказать теорему 2, теорему 3.
Литература:
Л.С.Атанасян. Геометрия, учебник для 10-11 классов.