Фиктивные переменные

Фиктивные переменные
На практике приходится учитывать в моделях факторы, носящие качественный характер, значения которых в наблюдениях не возможно измерить с помощью числовой шкалы.
Примеры.
Моделирование влияния пола специалистов на уровень зарплаты.
Моделирование доходов граждан от типа учебного заведения, в котором он получил образование (государственное, частное, специализированное,…)
Модель инфляции с учетом различных видов регулирования со стороны государства)

Фиктивные переменные
Возможны два подхода к решению задачи:
- построить несколько моделей отдельно для каждого значения (градации) качественной переменной
- учесть влияние качественного фактора в одной модели
Второй способ представляется более прогрессивным, т.к в этом случае появляется возможность оценить статистическую значимость влияния данного фактора на поведение эндогенной переменной на фоне других факторов, внесенных в спецификацию модели

Фиктивные переменные
Пример. Изучается зависимость расходов на образование «С» в «обычных» и «специализированных» школах в зависимости от числа учащихся N
Предположим:
Зависимость затрат на обучение от количества учащихся N в обоих типах школ одинакова
2. Разница в затратах объясняется необходимостью приобретения специализированного оборудования для обучения специальным дисциплинам
Тогда если строить различные модели для каждого типа школ, то спецификацию моделей можно записать в виде:
Yo = a0 + a1N +u
Ys = b0 + a1N + v

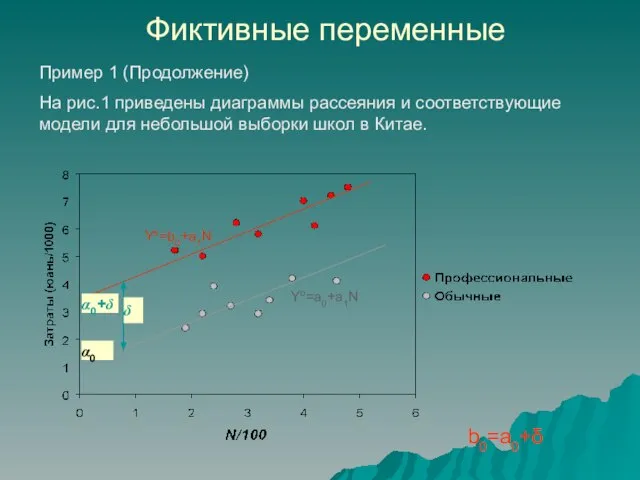
Фиктивные переменные
Пример 1 (Продолжение)
На рис.1 приведены диаграммы рассеяния и соответствующие модели для небольшой выборки школ в Китае.
α0
δ
α0+δ
Yo=a0+a1N
Ys=b0+a1N
b0=a0+δ

Фиктивная переменная сдвига
Обе модели можно объединить, если ввести переменную d, область определения которой два целых числа : 0 и 1. При этом:
Спецификация такой модели имеет вид:
Y = a0 + a1N + δd + u
Тогда при d=0 получим Yo = a0 + a1N + u
при d=1 получим Ys = (a0+δ) +a1N + v

Фиктивная переменная сдвига
Отметим:
Имея модель вида Y = a0 + a1N + δd + u, есть возможность после применения МНК оценить значения параметров a0, a1 и δ, стандартные ошибки их оценок, а следовательно, проверить гипотезу статистической значимости влияния фиктивной переменной d (влияние типа школ) на значения эндогенной переменной Y (затраты на обучение)
2. Графики моделей для d=0 и d=1 будут параллельны, т.к предполагается, влияние переменной N в обоих случаях остается неизменным

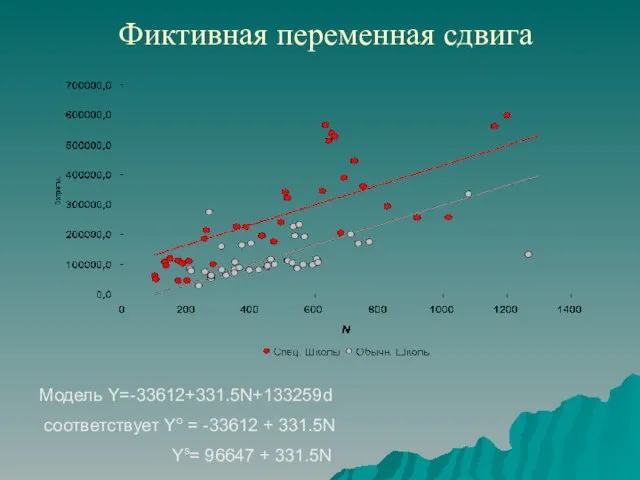
Фиктивная переменная сдвига
Модель Y=-33612+331.5N+133259d
соответствует Yo = -33612 + 331.5N
Ys= 96647 + 331.5N

Фиктивная переменная сдвига
Фиктивные переменные часто применяются при построении динамических моделей, когда с определенного момента времени начинает действовать какой-либо качественный фактор
Пример 2. Модель расходов на автотранспорт в Европе в период с 1963 по 1982 годы.
Замечание. В 1974 году в Европе начался крупный нефтяной кризис, который резко поднял цены на ГСМ.
В результате в 1974 году резко снизились расходы на автотранспорт, но затем затраты вновь стали расти с прежней скоростью.
Для учета этой ситуации вводится фиктивная переменная d, которая равна:

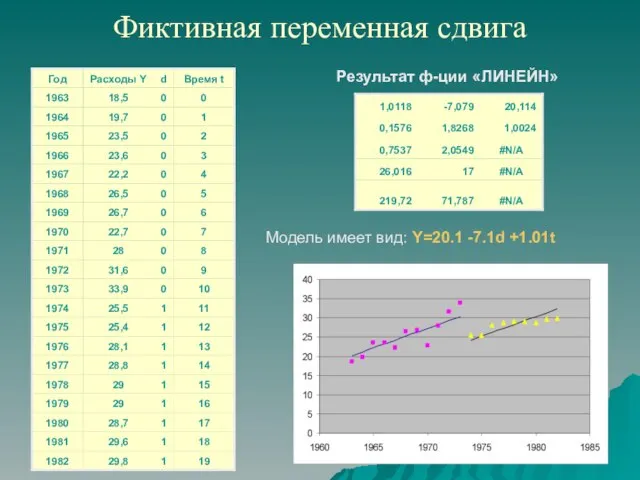
Фиктивная переменная сдвига
Результат ф-ции «ЛИНЕЙН»
Модель имеет вид: Y=20.1 -7.1d +1.01t

Фиктивная переменная сдвига
(общий случай)
Пусть некоторый качественный фактор имеет несколько градаций (более 2-х)
Введение в модель фиктивных переменных с несколькими градациями рассмотрим на примере шанхайских школ, где имеются 4 категории школ: общеобразовательные, технические, ПТУ и специализированные.
Казалось достаточно ввести фиктивную переменную сдвига d, придав ей четыре различных значения и проблема будет решена.
Такой подход мало эффективен, т.к не удается оценить статистическую значимость влияния каждой градации на значения эндогенной переменной

Фиктивная переменная сдвига
(общий случай)
В этом случае имеет смысл ввести отдельную переменную для каждой градации фактора.
Например:

Фиктивная переменная сдвига
(общий случай)
Однако, если взять спецификацию модели в виде:
Y=a0 + a1d1+a2d2+a3d3+a4d4+a5N+u
при этом всегда верно тождество d1+d2+d3+d4=1
Это означает, что матрица Х коэффициентов системы уравнений наблюдений будет коллинеарной т.к в ней присутствует столбец из 1, и как следствие отсутствует возможность применения МНК для оценки параметров модели.
Предлагается в спецификацию ввести (к-1) фиктивную переменную (к- кол-во градаций), сделав одну из градаций базовой, относительно которой изучать влияние остальных градаций. Проблемы мультиколинеарности в этом случае не возникает

Фиктивная переменная сдвига
(общий случай)
В рассматриваемом примере в качестве базового уровня можно принять градацию «Общеобразовательная»
Этой градации будет соответствовать состояние d2=d3=d4=0
Спецификация модели примет вид: Y=a0+a1N+a2d2+a3d3+a4d4+u (13.1)
Экономический смысл коэффициентов a2, a3, a4 – превышение стоимости образования в соответствующей школе по отношению к общеобразовательной
Из уравнения (13.1) легко получить соответствующее уравнение для каждого типа школ

Фиктивная переменная сдвига
(общий случай)
Y = a0 +a1N +U1 - Уравнение для общеобразовательных школ
Y =(a0+a2) +a1N + U2 - уравнение для «технических» школ
Y=(a0+a3) + a1N + U3 - уравнение для ПТУ
Y=(a0+a4) + a1N + U4 - уравнение для «специализированных» школ
Здесь также предполагается, что зависимость затрат на обучение от количества учащихся остается неизменной

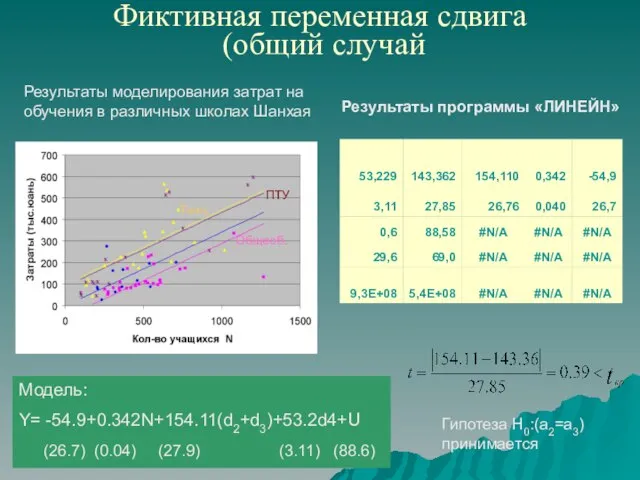
Фиктивная переменная сдвига
(общий случай
Результаты моделирования затрат на обучения в различных школах Шанхая
Модель:
Y= -54.9+0.342N+154.11(d2+d3)+53.2d4+U
(26.7) (0.04) (27.9) (3.11) (88.6)
Результаты программы «ЛИНЕЙН»
Гипотеза H0:(a2=a3) принимается
Общеоб.
Техн.
ПТУ

Фиктивные переменные сдвига в моделях временных рядов
Пример. Модель зависимости расходов на электроэнергию и газ в США за период 1977-1982г.г.

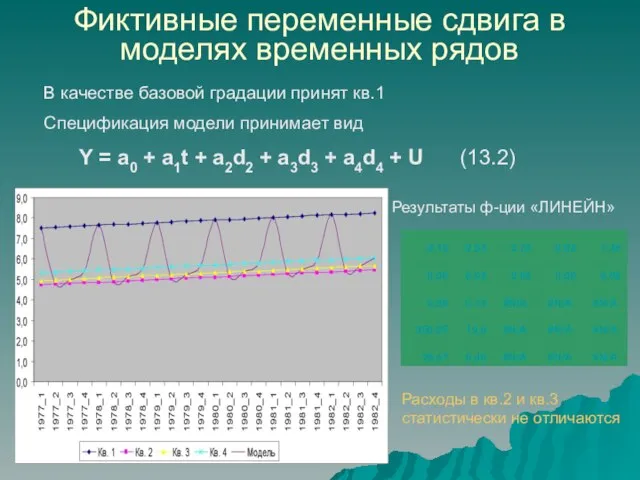
Фиктивные переменные сдвига в моделях временных рядов
В качестве базовой градации принят кв.1
Спецификация модели принимает вид
Y = a0 + a1t + a2d2 + a3d3 + a4d4 + U (13.2)
Результаты ф-ции «ЛИНЕЙН»
Расходы в кв.2 и кв.3 статистически не отличаются

Фиктивные переменные наклона
Во всех рассмотренных примерах априори предполагается, что различные градации качественного фактора приводят к параллельному сдвигу «базовой» модели
Это допущение не бесспорно!
В примере с различными типами школ в Шанхае предполагалось, что зависимость расходов на обучение от кол-ва учеников во всех школах одинаково
Вопрос. Как учесть эффект влияния типа школы на зависимость затрат от кол-ва учащихся?

Фиктивные переменные наклона
Для учета возможного изменения наклона графика модели при изменении градации качественного фактора предлагается ввести в спецификацию модели еще одно слагаемое вида «d умноженное на x»
Вернемся к примеру изучения зависимости расходов на образование в различных школах. Для простоты ограничимся лишь двумя градациями фактора «тип школы»: d=0 – обычная школа;
d=1 – профессиональная школа.
Спецификацию модели следует записать в виде:
Y = a0 + a1N + a2*d + a3dN +U (13.3)

Фиктивные переменные наклона
С помощью модели (13.3) появляется возможность оценить изменения наклона «базовой модели» при переходе изменении градации фактора (переменной d)
Пусть d=0, тогда модель (13.3) принимает вид:
Y= a0 + a1N +U1 (13.4)
При d=1 получим:
Y= a0 +a1N +a2 +a3N +U2
или Y= (a0+a2) + (a1+a3)N +U2 (13.5)
Модель (3.5), соответствующая d=1 отличается коэффициентами регрессии от модели (13.4)
В ней учитывается как «параллельный» сдвиг, так и изменение угла наклона (изменение коэффициента a1)