Содержание
- 2. Одно из главных требований ФГОС: создание современной информационно-образовательной среды Комплекс информационно-образовательных ресурсов взамен традиционных предметных комплектов;
- 3. Место и роль экспериментальных заданий при изучении физики: составляют неотъемлемую часть изучаемой дисциплины; способствуют более глубокому
- 4. I. Творческие задания Практическое задание “Шагающий человек” Цель работы: оценить мощность, развиваемую пешеходом при ходьбе; Мощность
- 5. Физическая модель явления Идея решения: когда человек делает шаг, его центр масс C поднимается на некоторую
- 6. Некоторые численные оценки Если v =4 км/ч, t =1 мин, то пройденный путь s ≈66 м.
- 7. Практическая работа «Взаимодействие магнита с железной пластиной Оборудование: подковообразный магнит; железная пластина; динамометр Бакушинского; нить
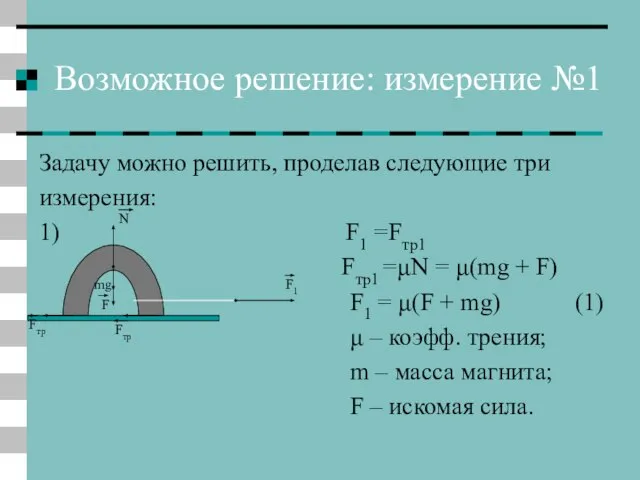
- 8. Возможное решение: измерение №1 Задачу можно решить, проделав следующие три измерения: 1) F1 =Fтр1 Fтр1 =μΝ
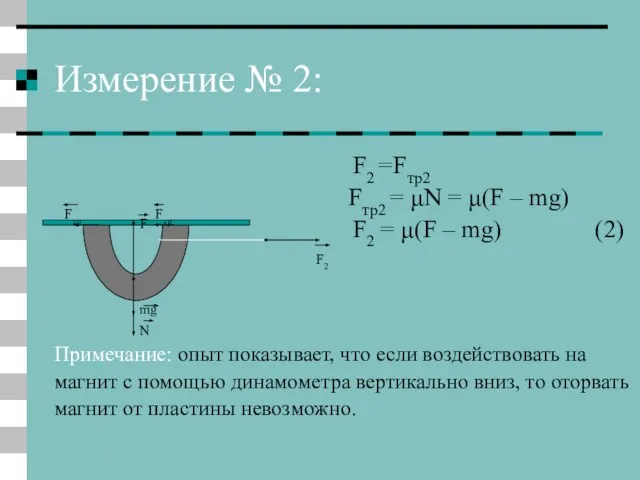
- 9. Измерение № 2: F2 =Fтр2 Fтр2 = μN = μ(F – mg) F2 = μ(F –
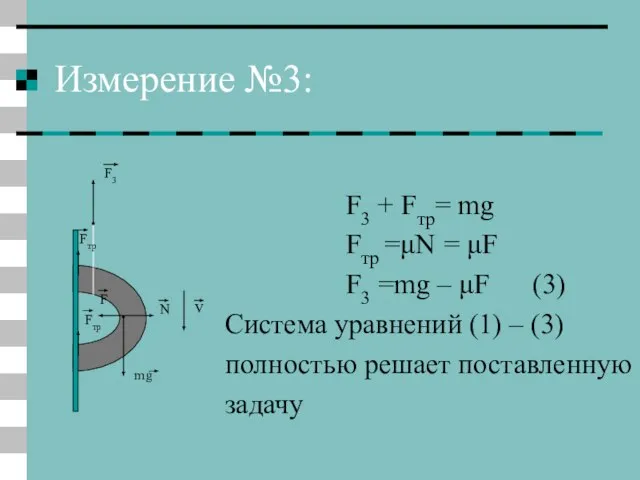
- 10. Измерение №3: F3 + Fтр= mg Fтр =μΝ = μF F3 =mg – μF (3) Система
- 11. Практическая работа “Оценка радиуса микропузырька в воде” Оборудование: мензурка с водой; соль; линейка; секундомер; справочник физических
- 12. Физическая модель явления Т. к. v =const, для пузырька выполняется условие равновесия: FA =Fc FA Fc
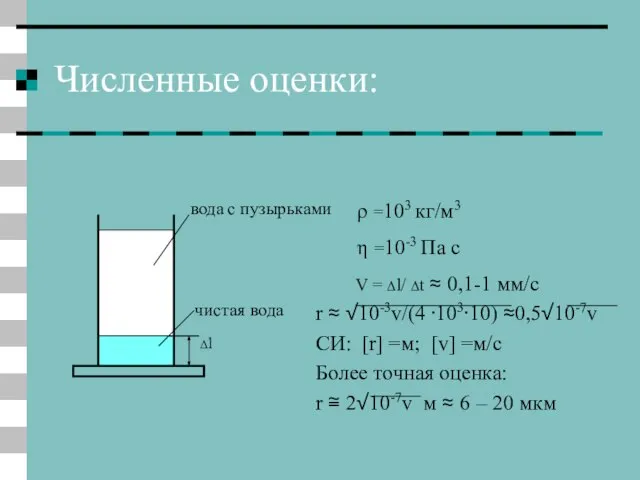
- 13. Численные оценки: Δl вода с пузырьками чистая вода ρ =103 кг/м3 η =10-3 Па с V
- 14. Практическая работа “Оценка толщины стенки мыльного пузыря” Оборудование: мыльный пузырь,выдутый через трубочку; рулетка; секундомер; справочник физических
- 15. Физическая модель явления: v =const mg =Fc+ FA - условие равновесия FA =4/3⋅πρвозgR3 –сила Архимеда, R
- 16. Численные оценки: Высота падения пузыря h ≈ 2 м, время падения t ≈ 3 c; радиус
- 17. Практическая работа “ Плавающее сито”. Оборудование: металлическое сито; динамометр; линейки; набор грузов; сосуд с водой.
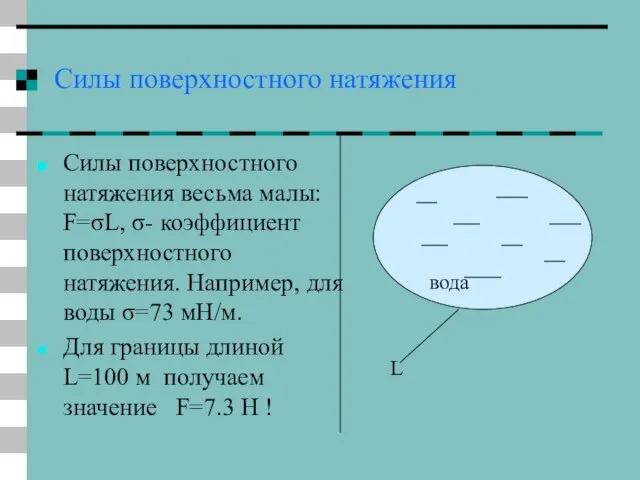
- 18. Силы поверхностного натяжения Силы поверхностного натяжения весьма малы: F=σL, σ- коэффициент поверхностного натяжения. Например, для воды
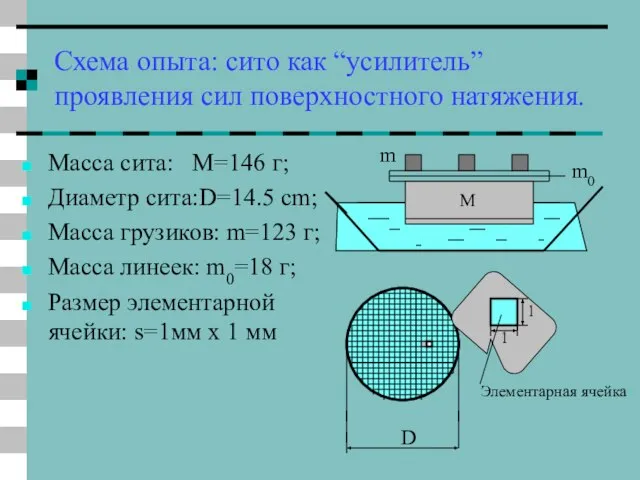
- 19. Схема опыта: сито как “усилитель” проявления сил поверхностного натяжения. Масса сита: M=146 г; Диаметр сита:D=14.5 cm;
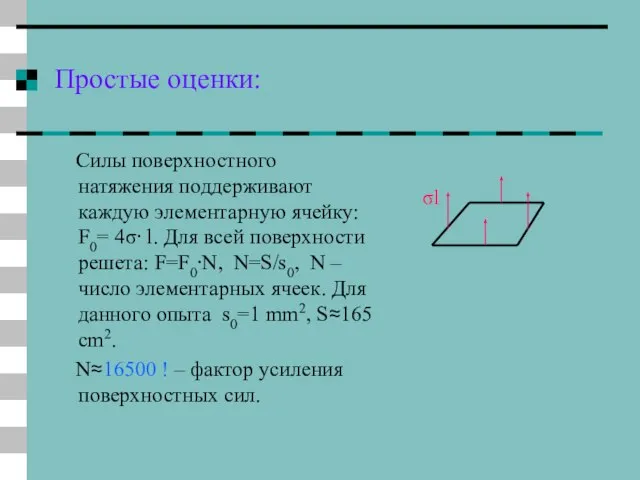
- 20. Простые оценки: Силы поверхностного натяжения поддерживают каждую элементарную ячейку: F0= 4σ⋅ l. Для всей поверхности решета:
- 21. Оценка коэффициента поверхностного натяжения воды из условия плавания сита Пренебрегая незначительным вкладом архимедовой выталкивающей силы, запишем
- 22. Практическая работа “Взаимодействие гладких стеклянных пластин” Оборудование: две гладкие стеклянные пластины; линейка; микрометр; пипетка; вода.
- 23. Физическая картина явления В результате смачивания поверхностей пластин водой, боковые поверхности слоя воды между пластинами оказываются
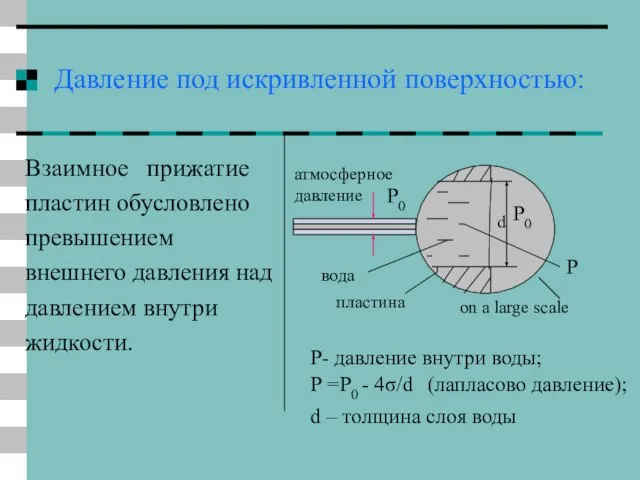
- 24. Давление под искривленной поверхностью: Взаимное прижатие пластин обусловлено превышением внешнего давления над давлением внутри жидкости. on
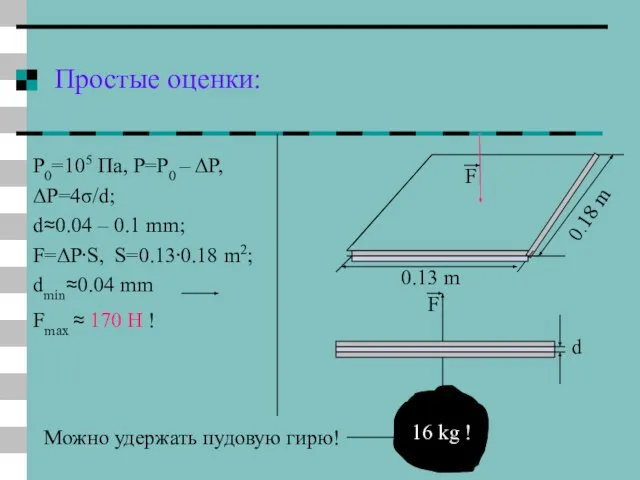
- 25. Простые оценки: P0=105 Пa, P=P0 – ΔP, ΔP=4σ/d; d≈0.04 – 0.1 mm; F=ΔP⋅S, S=0.13⋅0.18 m2; dmin≈0.04
- 26. Проект “Жизнь мыльного пузыря”: 1. Зависимость времени жизни мыльной пленки от влажности воздуха Вопросы: а) какие
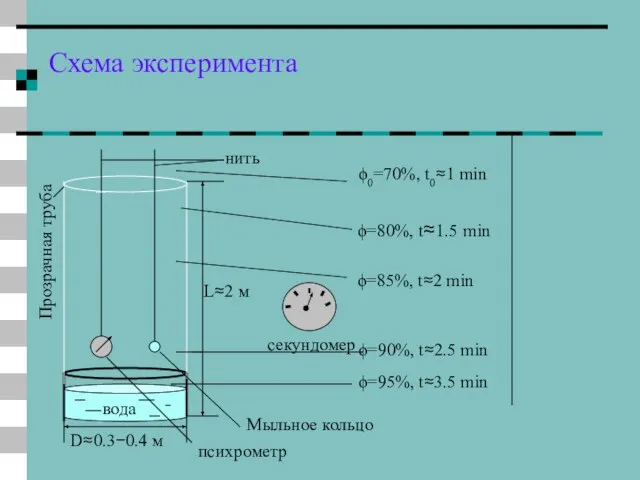
- 27. Схема эксперимента вода психрометр Мыльное кольцо L≈2 м нить Прозрачная труба ϕ0=70%, t0≈1 min ϕ=80%, t≈1.5
- 28. Анимация эксперимента Зависимость времени жизни мыльной пленки от влажности воздуха
- 29. Простая модель явления d –толщина мыльной пленки vd=vисп-vконд; влажный воздух ϕ=100% d Сухой воздух ϕ=50-60% Vконд∝
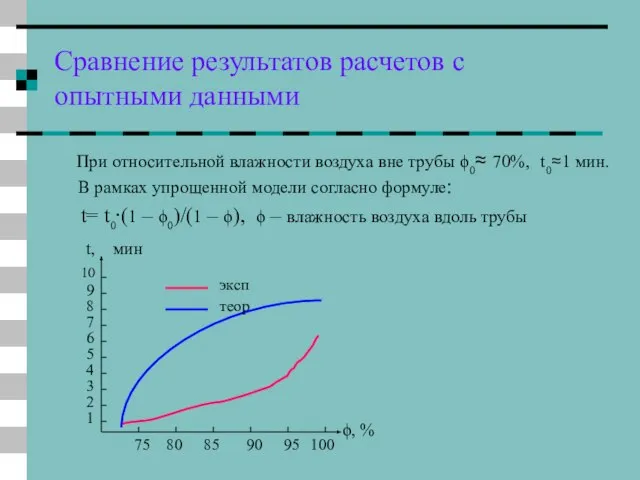
- 30. Сравнение результатов расчетов с опытными данными При относительной влажности воздуха вне трубы ϕ0≈ 70%, t0≈1 мин.
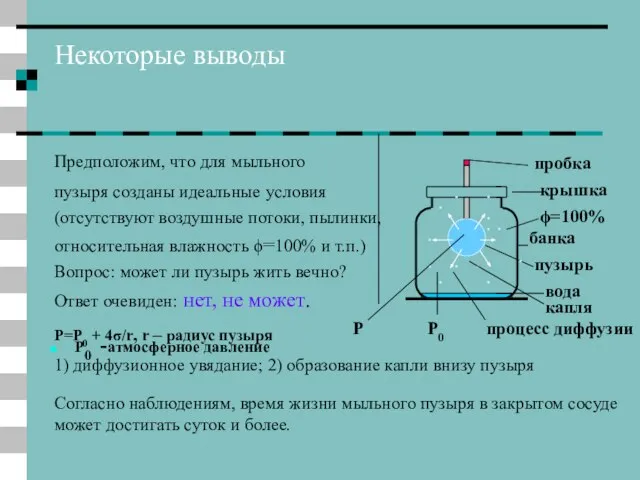
- 31. Некоторые выводы Предположим, что для мыльного пузыря созданы идеальные условия (отсутствуют воздушные потоки, пылинки, относительная влажность
- 32. Проект «Жизнь мыльного пузыря”: 2. Время сдувание мыльного пузыря
- 33. The objects of investigations are the air and water streams. There are the opportunities to intensificate
- 34. Sounding tube – the thermal autogenerator of sound Equipment: glass tube about 80 – 100 cm;
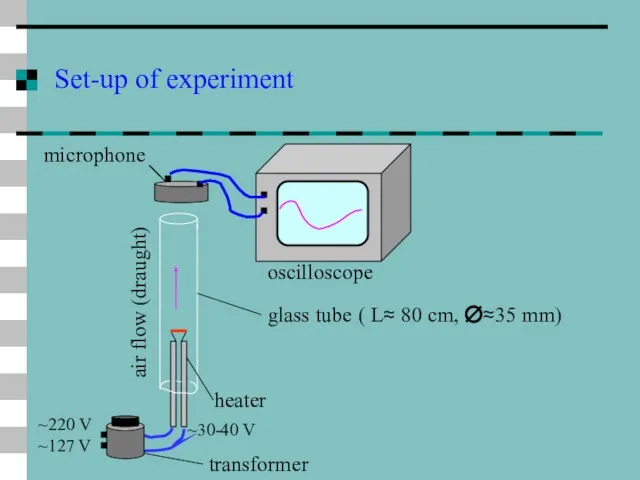
- 35. Set-up of experiment ~220 V ~127 V ~30-40 V heater air flow (draught) oscilloscope microphone glass
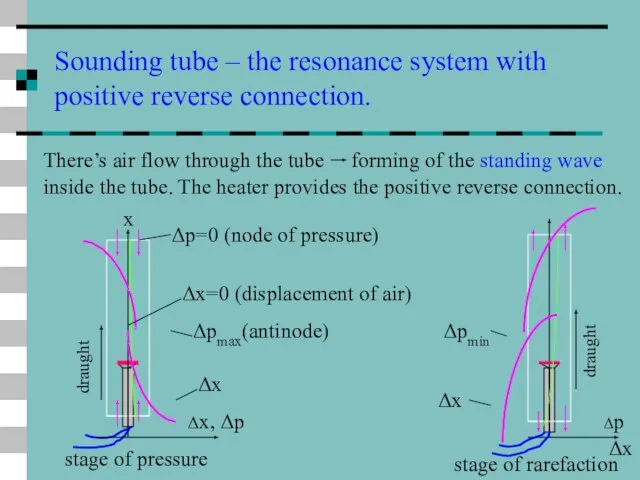
- 36. Sounding tube – the resonance system with positive reverse connection. There’s air flow through the tube
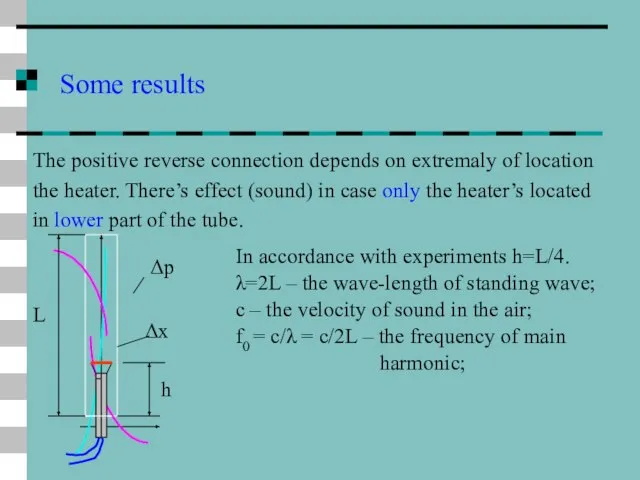
- 37. Some results The positive reverse connection depends on extremaly of location the heater. There’s effect (sound)
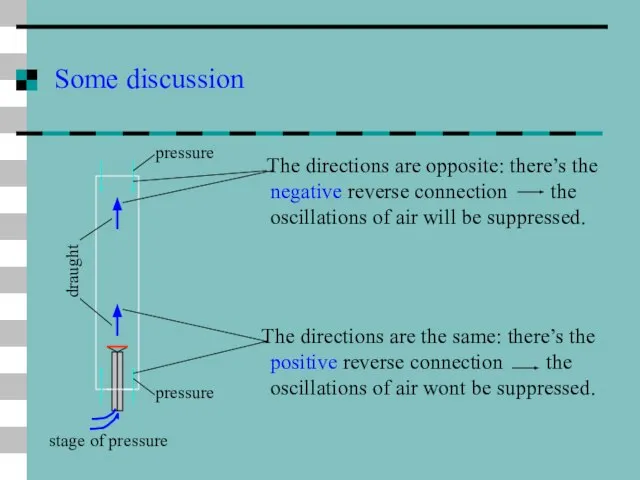
- 38. Some discussion The directions are opposite: there’s the negative reverse connection the oscillations of air will
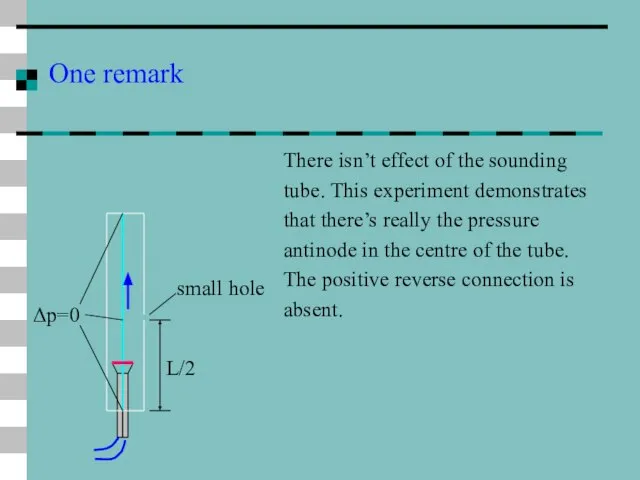
- 39. One remark There isn’t effect of the sounding tube. This experiment demonstrates that there’s really the
- 40. The water streams Introduction: There are some questions: a) can we observe the process of disintegration
- 41. Equipment: volume about 5 litres (vessel for water); rubber or plastic hose about 2 m, ∅=10-15
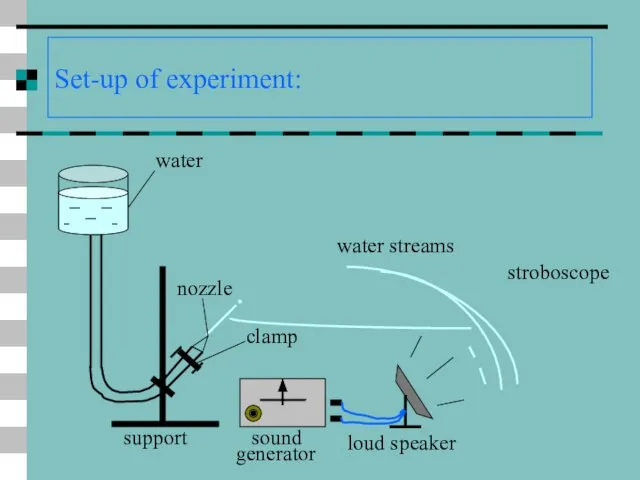
- 42. Set-up of experiment: sound generator support water clamp nozzle loud speaker water streams stroboscope .
- 43. Some discussion. It’s necessary to have a stroboscope to observe the dropping structure of water stream.
- 44. Some estimations: There’s the simple estimation for λ: λ >9/2⋅r, r ≈ 0.5 mm – radius
- 50. Скачать презентацию





























 (–1) · 3 =
(–1) · 3 = Осмотр общего имущества в многоквартирном доме
Осмотр общего имущества в многоквартирном доме EV3 Самосвал
EV3 Самосвал Инвестиционный фонд МАП «Инновационный лифт»
Инвестиционный фонд МАП «Инновационный лифт» Нам нужны союзники!
Нам нужны союзники! Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3
Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3 Мое зазеркалье
Мое зазеркалье Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем
Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем Презентация Microsoft PowerPoint (3)
Презентация Microsoft PowerPoint (3) Презентация на тему Иудаизм презентация 4 класс
Презентация на тему Иудаизм презентация 4 класс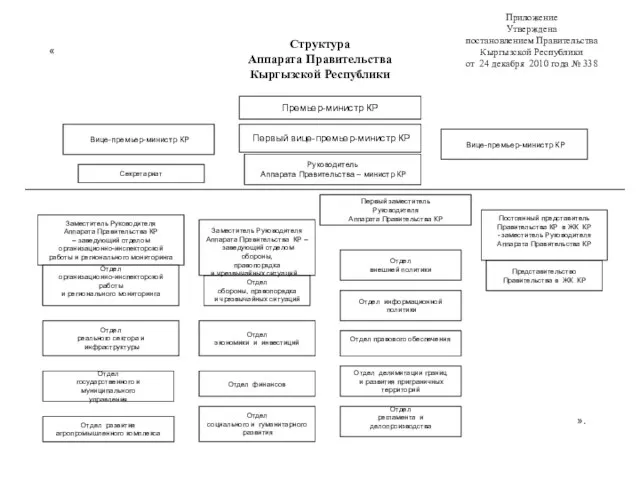 Структура Аппарата Правительства Кыргызской Республики
Структура Аппарата Правительства Кыргызской Республики Автоматизированная информационная система «Государственный заказ»
Автоматизированная информационная система «Государственный заказ» Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов
Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов Тема урока «Право на труд. Трудовые правоотношения»
Тема урока «Право на труд. Трудовые правоотношения» Класс 1-1 3주 후 시험문제 읽기 Чтение
Класс 1-1 3주 후 시험문제 읽기 Чтение Обобщающий урок - игра по теме: «Я знаю край родной».
Обобщающий урок - игра по теме: «Я знаю край родной». Тяжелая атлетика в России и за рубежом
Тяжелая атлетика в России и за рубежом Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Лекция_6 ЭТД ФТД.ppt
Лекция_6 ЭТД ФТД.ppt Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс
Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс Методы мониторинга репутациив социальных медиа
Методы мониторинга репутациив социальных медиа Областной конкурспервичных профсоюзныхорганизаций.
Областной конкурспервичных профсоюзныхорганизаций. Контроль квалификации сварщиков. Система аттестации сварочного производства
Контроль квалификации сварщиков. Система аттестации сварочного производства Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1)
Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1) 36736
36736 Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс)
Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс) Электрическая лампа накаливания
Электрическая лампа накаливания 20161206_avstraliya-i-okeaniya
20161206_avstraliya-i-okeaniya