Физика рассеяния света

Диэлектрические шары без поглощения
Только последние годы расчеты по теории Mie
стали делом заурядным
области, отмеченные одной циф-рой, определяются одним, ярко выраженным эффектом
области, отмеченные двумя цифрами, занимают промежу-точное положение, где имеют место эффекты обоих областей

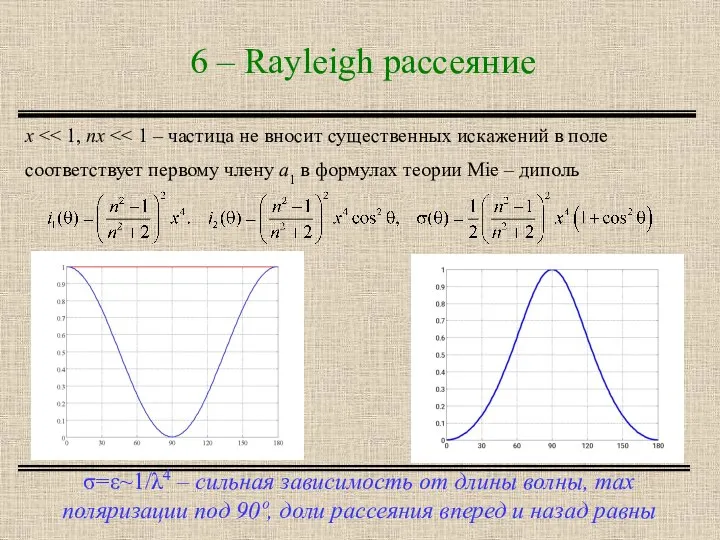
6 – Rayleigh рассеяние
σ=ε~1/λ4 – сильная зависимость от длины волны, max поляризации под 90º, доли рассеяния вперед и назад равны
x << 1, nx << 1 – частица не вносит существенных искажений в поле
соответствует первому члену a1 в формулах теории Mie – диполь

56 – Рост размеров частиц
вперед/назад > 1 – рост доли рассеянного вперед – эффект Mie
максимум поляризации смещается в область углов θ>90º и уменьшается (<1)
остаточный голубой свет при 90º - i1 и i2 неодинаково зависят от длины волны
С ростом размеров частиц необходимо учитывать все большее число членов ряда. что приводит:
Релеевское рассеяние не чувствительно ни к форме,
ни к размерам частиц

5 – оптический резонанс
На кривой ослабления пики, индикатриса рассеяния и кривая поляризации приобретает крайне сложный, капризный вид
с дальнейшим ростом оптических размеров частицы наиболее существенными становятся члены с большими номерами
периодически возникают стоячие волны в частице, для которых наблюдается оптический резонанс – стоячие волны, удерживаемые на шаре

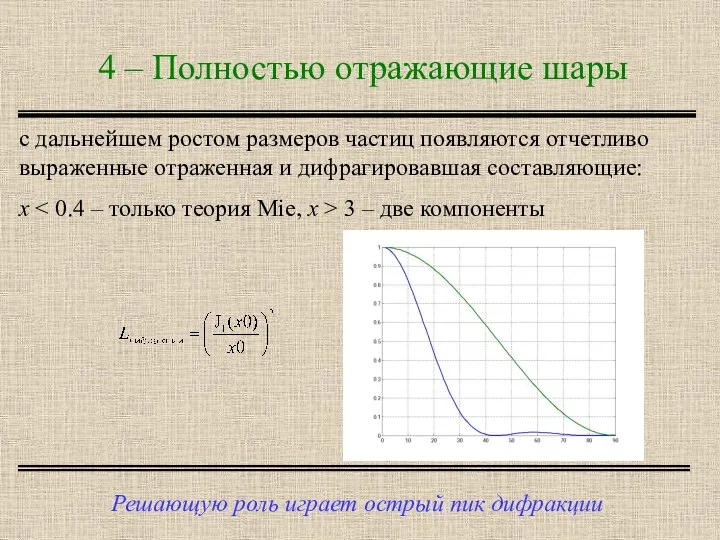
4 – Полностью отражающие шары
Решающую роль играет острый пик дифракции
с дальнейшем ростом размеров частиц появляются отчетливо выраженные отраженная и дифрагировавшая составляющие:
x < 0.4 – только теория Mie, x > 3 – две компоненты

3 – область геометрической оптики
Радуги, глории не могут быть вычисленны в приближении ГО
с уменьшением показателя преломления n появляется все более выраженная преломленная компонента
геометрическая оптика (отражение+преломление) + дифракция
отраженная и преломленная компоненты сильно поляризованы
Qe = 2 – парадокс рассеяния

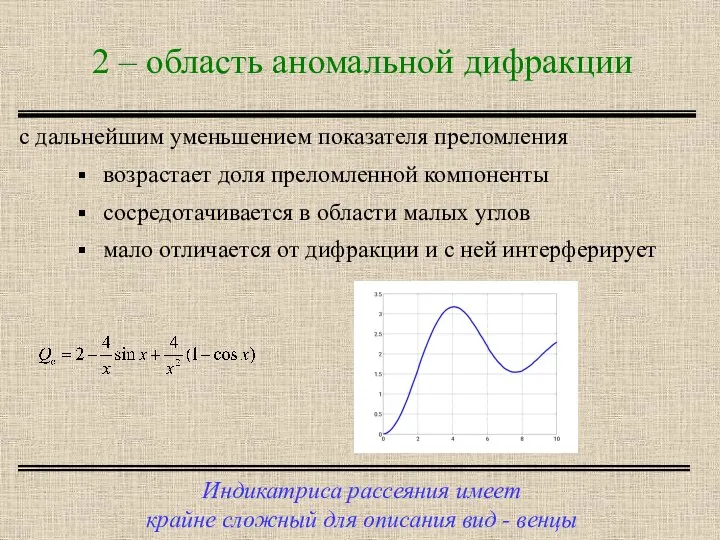
2 – область аномальной дифракции
Индикатриса рассеяния имеет
крайне сложный для описания вид - венцы
с дальнейшим уменьшением показателя преломления
возрастает доля преломленной компоненты
сосредотачивается в области малых углов
мало отличается от дифракции и с ней интерферирует

1 – область Rayleigh-Hans
Расчет возможен для частиц произвольной формы
уменьшение размеров приводит
к уменьшению фазового сдвига между преломленной и отраженной компонентами
уменьшает дифракцию
компоненты становятся неразличимы
каждый элемент объема рассеивает по Rayleigh, а суммарная волна – интерференция волн от этих элементов