Физика Солнца

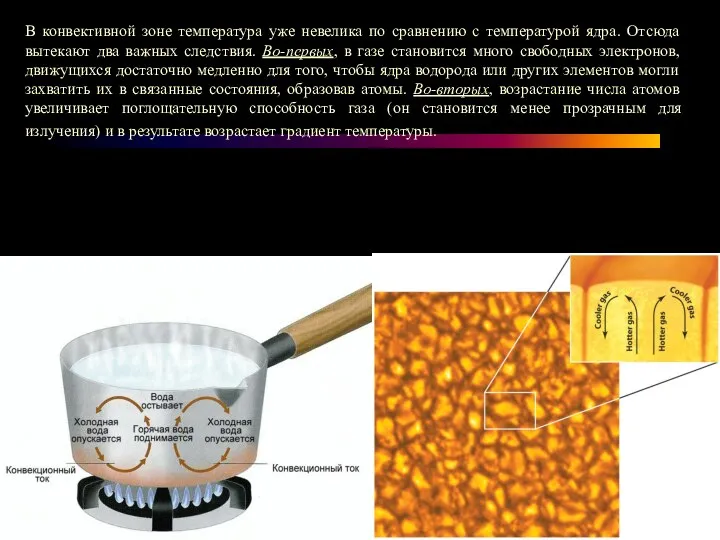
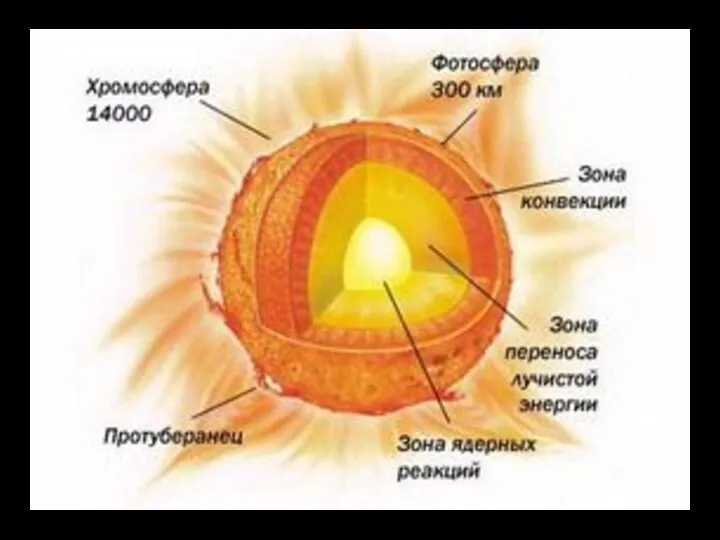
В конвективной зоне температура уже невелика по сравнению с температурой ядра. Отсюда вытекают два важных следствия. Во-первых, в газе становится много свободных электронов, движущихся достаточно медленно для того, чтобы ядра водорода или других элементов могли захватить их в связанные состояния, образовав атомы. Во-вторых, возрастание числа атомов увеличивает поглощательную способность газа (он становится менее прозрачным для излучения) и в результате возрастает градиент температуры.

По мере приближения к фотосфере изнутри коэффициент поглощения χ продолжает увеличиваться. Однако плотность газа резко убывает, и величина 1/ρχ - среднее расстояние, проходимое фотоном без рассеяния или перепоглощения (средняя длина свободного пробега фотона), - быстро растёт и достигает величины того же порядка, что и шкала высот атмосферы Н. Если 1/ρχ<
>H, то испущенные фотоны беспрепятственно пройдут расстояние Н и оставшуюся часть атмосферы, плотность которой непрерывно уменьшается с высотой, и уйдут из Солнца. Слой, где 1/ρχ≅Н, - это именно та область, из которой уходит прямо во внешнее пространство большая часть излучения.
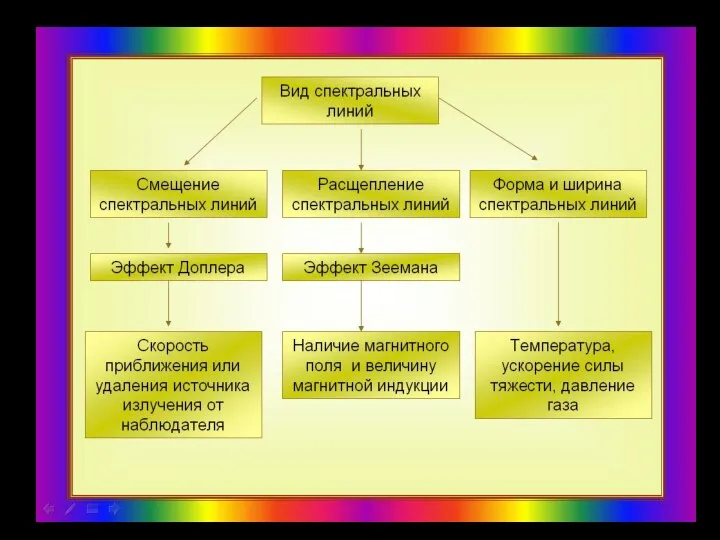
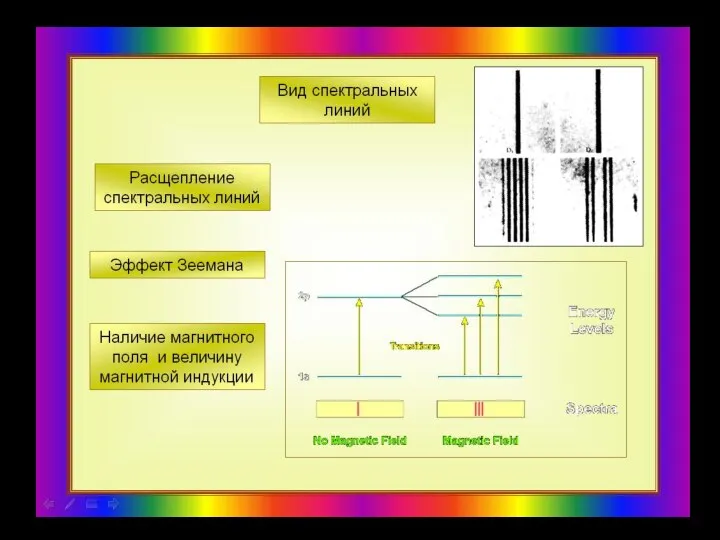
До сих пор мы рассматривали только непрерывное излучение, испускаемое фотосферой. Единственными негладкими участками на кривой зависимости интенсивности от длины волны были пределы спектральных серий. Однако в наблюдаемом спектре содержится, кроме того, множество линий поглощения, называемых фраунгоферовыми линиями, которые на графике интенсивности имеют вид крутых узких углублений. Фраунгоферовы линии дают множество детальных сведений об атмосфере Солнца, включая температуру, давление, динамику, химический состав и локальные значения напряжённости магнитного поля.

Эрвин Шредингер имел удивительно широкий круг интересов: радиоактивность и её связь с атмосферным электричеством, электротехника, акустика и оптика, квантовая физика. Он изучил шесть иностранных языков, хорошо знал немецких поэтов, сам писал стихи.
Наличие волновых свойств у электронов (волны де Бройля) Шредингер принял как фундаментальный экспериментальный факт. Для физики волны далеко не были чем-то новым. Было хорошо известно, что любая волна (например, волна плотности электрического заряда) подчиняется волновому уравнению:
Δρ-c-2(∂2/∂t2)ρ=0 (1)
где Δ=∂2/∂x2+∂2/∂y2+∂2/∂z2 – оператор Лапласа, с – фазовая скорость волны.
А если это – волна де Бройля? Длина такой волны λ=h/p, частота ν=E/h, фазовая скорость c=λν=E/p (p,E – импульс и энергия электрона, h – постоянная Планка). Но, как мы знаем, электрон – это компактный пространственный объект, тогда как его волна де Бройля (как и любая другая волна) – это процесс, который может захватить, вообще говоря, всё пространство. Стало быть такая волна “размазывает” заряд электрона e по пространству и можно говорить о пространственном распределении заряда ρ(x,y,z,t)=eΨ(x,y,z,t)? Если формально подставить это распределение в волновое уравнение (1), то, естественно, получим волновое уравнение на Ψ:
ΔΨ-(p/E)2(∂2/∂t2)Ψ=0 (2)

Если энергия электрона Е равна сумме его кинетической и потенциальной энергии E=p2/2m+U, то (p/E)2=2m(E-U)/E2. Положим (разделяем переменные):
Ψ(x,y,z,t)=u(x,y,z)exp(-iωt), ω=2πν (3)
Подставляя (3) в (2) и учитывая, что Е=hω, h= h/2π и ωu=-(1/i)exp(iωt)(∂/∂t)Ψ получим:
Δu+(2m/h)iexp(iωt)(∂/∂t)Ψ-(2m/h2)Uu=0 (4)
Умножая (4) на exp(-iωt) получаем:
ih(∂/∂t)Ψ=-(h2/2m)ΔΨ+UΨ (5)
Волновое уравнение (5), которому подчиняется волна де Бройля – это и есть знаменитое уравнение Шредингера – первое уравнение квантовой механики, опубликованное Эрвином Шредингером в 1926 году в серии работ под общим названием “Квантование как задача о собственных значениях”. Оно позволяет найти функцию Ψ.

Но как, зная функцию Ψ, найти импульс волны де Бройля? В качестве примера рассмотрим монохроматическую волну де Бройля, бегущую вдоль оси x:
Ψ=Aexp[-(i/h)(Et-px) (6)
и продифференцируем функцию Ψ по координате:
(∂/∂x)Ψ=(i/h)pAexp[-(i/h)(Et-px)=(i/h)pΨ ? -ih(∂/∂x)Ψ=pΨ (7)
Таким образом, значение импульса p появляется в виде множителя перед функцией Ψ, если применить к этой функции математическую операцию -ih(∂/∂x). Можно об этом сказать и по другому: операция -ih(∂/∂x) ставит функции Ψ в соответствие функцию pΨ. Когда математики говорят, что задана функция, то подразумевают, что им известно правило, по которому одним числам (аргументу функции x) ставятся в соответствие другие числа (значение функции f(x)). Если же им известно правило, по которому одной функции ставится в соответствие другая функция, то они говорят, что задан оператор. Обозначив через Px=-ih(∂/∂x) перепишем уравнение (7) в виде:
PxΨ=pΨ (8)
Функцию Ψ, удовлетворяющую уравнению (8), математики называют собственной функцией оператора Px, величину p в этом уравнении – собственным значением этого оператора, а само уравнение (8) – задачей о собственных значениях. Из равноправия осей x,y,z следует, что операторы, соответствующие составляющим импульса по осям y и z, имеют вид Py=-ih(∂/∂y) и Pz=-ih(∂/∂z).

Если дважды последовательно применить оператор Px к функции Ψ, то получим:
Px2Ψ=PxPxΨ=-ih(∂/∂x)[-ih(∂/∂x)Ψ]=-h2(∂2/∂x2)Ψ
Следует иметь в виду, что Px2 – это просто обозначение последовательного применения оператора Px к одной и той же функции Ψ. Соответственно Py2= -h2(∂2/∂y2), Pz2= -h2(∂2/∂z2), а сумма –(h2/2m)[(∂2/∂x2)+(∂2/∂y2)+(∂2/∂z2)]= –(h2/2m)Δ представляет собой оператор кинетической энергии. Потенциальная энергия U зависит только от координат, но не от импульсов. Поэтому оператор потенциальной энергии – это просто умножение функции Ψ на функцию U. Таким образом, оператор полной энергии естественно определить как
H=–(h2/2m)Δ+U
Оператор H называется оператором Гамильтона (или гамильтонианом). Через оператор Гамильтона уравнение Шредингера можно переписать в виде:
ih(∂/∂t)Ψ=HΨ

Подставив в уравнение (5) формулу (3), в которой положим ω=Е/h, получим:
Eu=-(h2/2m)Δu+Uu (9)
Максимально упростим себе жизнь, считая u(x,y,z)=u(x). В этом случае уравнение (9) записывается в виде:
(d2/dx2)u+(2m/h2)(E-U)u=0 (10)
Задавая потенциальную энергию U как функцию координат и условия на границах области, захваченной волновым процессом, можно судить о свойствах волны де Бройля в этой области пространства. В качестве простейшего примера рассмотрим так называемую потенциальную яму с бесконечно высокими стенками, то есть предположим, что волновой процесс ограничен в пространстве сегментом 0 ≤ x ≤ a, причём u(0)=u(a)=0, U(x)=0 при 0 ≤ x ≤ a, U(x)=∞ при x<0 или x>a. Тогда внутри сегмента 0 ≤ x ≤ a уравнение (10) вырождается в известное всем уравнение гармонических колебаний:
(d2/dx2)u+(2m/h2)Eu=0,

решение которого, удовлетворяющее условию u(0)=0, имеет вид:
u(x) ~ sin[(2mE/h2)1/2x].
Наличие второго граничного условия u(a)=0 означает, что
sin[(2mE/h2)1/2a]=0.
Последнее можно обеспечить лишь при условии, что
(2mE/h2)1/2a=πn, n=1,2,3,…..(11)
Следовательно En=(1/2m)(πhn/a)2 и энергия волны оказывается квантованной даже в рассмотренном простейшем случае. Причина этого – условие (11), то есть ограниченность области пространства, захваченной волновым процессом: если уж волновой процесс де Бройля развился в ограниченной области пространства (наподобие стоячей волны в ванне с водой), то необходимость поддерживать целое число полуволн в области пространства конечных размеров ограничивает допустимые значения длины волны (а значит и её энергии) числами из дискретного ряда – спектра.

В случае однородного поля H, направленного вдоль оси z, уравнение Шредингера имеет вид:
Характерный магнитный момент eh/2mc называют магнетоном Бора. В сферических координатах:
Если перейти к сферическим координатам, то z-компонента оператора момента импульса равна:
уравнение Шредингера перепишется в виде:

Если искать решение этого уравнения в виде (сферические функции – это собственные функции оператора проекции углового момента на ось z):
тогда вклад магнитного поля в уравнение имеет вид:
а само уравнение запишется в виде:
Это уравнение по форме совпадает с уравнением Шредингера для случая H=0. Отсюда следует, что:
Здесь En,l0 обозначены собственные значения для случая H=0. μ=0, ±1,±…±l.

В отсутствие магнитного поля энергия электрона не зависит от его магнитного момента, обусловленного орбитальным движением. При наличии магнитного поля энергия электрона будет зависеть уже от величины и ориентации орбитального магнитного момента. Вследствие этого энергетические уровни, отвечающие электронам с одним и тем же l, но разным μ, совпадающие при отсутствии магнитного поля, теперь расщепятся на столько уровней, сколько значений может принимать μ.

Звуковые волны, возникающие в конвективной зоне, распространяются наружу, перенося поток энергии, равный:
где Vwrms – среднеквадратичная скорость газа на фронте волны, а V0 – локальная скорость звука. Чтобы этот поток энергии оставался при распространении волны наружу почти постоянным, Vwrms должна увеличиваться при убывании плотности. Если направленный наружу поток энергии равен 107 эрг/(см2 сек) то в верхней части конвективной зоны Vwrms ~ 10-2V0. Поскольку скорость звука V0 изменяется в фотосфере и нижней хромосфере лишь очень незначительно, то при уменьшении плотности в 10000 раз (происходящем на протяжении первых 1000 км) скорость вещества должна возрасти до скорости звука. В результате образуется ударный фронт, в котором давление газа, плотность и температура изменяются скачкообразно на протяжении нескольких средних длин свободного пробега частиц. Изменения, происходящие в газе перестают быть обратимыми в термодинамическом смысле, и проходящий фронт оставляет за собой газ с более высокой температурой, так как некоторая часть энергии фронта рассеивается, нагревая атмосферу.
Для того, чтобы нагревание ударными волнами уравновешивало потери на излучение, волны должны иметь периоды, приблизительно равные 10 сек. Такие волны нельзя наблюдать непосредственно с доступной в настоящее время разрешающей способностью, так как их длина должна быть меньше 100 км.

В совокупности следующих одна за другой звуковых волн каждая последующая волна перемещается по газу, возмущённому предыдущими волнами. В адиабатическом и изэнтропическом движении сжатие газа сопровождается его подогревом, а скорость распространения возмущений возрастает с температурой. Поэтому каждая последующая волна будет перемещаться относительно невозмущённого газа несколько быстрее, чем предыдущая. Волны будут догонять друг друга, складываться и образовывать одну мощную волну сжатия, называемую ударной волной.
Фронт ударной волны представляет поверхность разрыва параметров состояния газа, перемещающуюся по газу и вызывающую скачкообразное изменение этих парамеров, причём невозмущённый газ перед фронтом ударной волны имеет меньшие давления, плотность и температуру, чем после прохождения фронта. Наличие очень резкого изменения параметров газа на участке, имеющем длину порядка пути свободного пробега иона, показывает, что здесь имеет место внутренний процесс, связанный с переходом кинетической энергии упорядоченного течения газа в кинетическую энергию беспорядочного теплового движения атомов. Этим объясняется разогрев газа при прохождении его из невозмущённой области перед фронтом ударной волны в область возмущённого движения за фронтом ударной волны.

=pn+ρu(un) - тензор плотности потока импульса (поток вектора импульса в направлении n, т.е. через поверхность, перпендикулярную к n). В частности, выбирая направление единичного вектора n вдоль направления скорости жидкости, мы найдём, что в этом направлении переносится лишь продольная компонента импульса, причём плотность её потока равна p+ρu2
ρ1u1=ρ2u2
p1+ρ1u12=p2+ρ2u22
cpT1+u12/2=cpT2+u22/2, T1=p1/(Rρ1), T2=p2/(Rρ2)