Измерение информации: алфавитный подход

Как измерить информацию?
Вопрос: «Как измерить информацию?» очень непростой.
Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.

Алфавитный подход к измерению информации
Познакомимся с способом измерения информации, который не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Применение алфавитного подхода удобно прежде всего при использовании технических средств работы с информацией. В этом случае теряют смысл понятия «новые — старые», «понятные — непонятные» сведения. Алфавитный подход является объективным способом измерения информации в отличие от субъективного содержательного подхода.

Алфавит и его мощность
Все множество используемых в языке символов будем традиционно называть алфавитом.
Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита.
Будем обозначать эту величину буквой N. Например, мощность алфавита из заглавных русских букв и отмеченных дополнительных символов равна 54.
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЪЭЮЯ0123456789().,!?«»:-; (пробел)

Сколько информации несет один символ в русском языке
Представьте себе, что текст к вам поступает последовательно, по одному знаку, словно бумажная ленточка, выползающая из телеграфного аппарата. Предположим, что каждый появляющийся на ленте символ с одинаковой вероятностью может быть любым символом алфавита.
В каждой очередной позиции текста может появиться любой из N символов.
Тогда, согласно известной нам формуле 2I = N , каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54.
Получаем: I = 5.755 бит.
Вот сколько информации несет один символ в русском тексте!

Количество информации в тексте
А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I.
Посчитаем количество информации на одной странице книги.
Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50x60=3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.

Задание 1:
Определите информационный объем страницы книги, если для записи текста использовались только заглавные буквы русского алфавита, кроме буквы Ё.
Решение:
N = 32
2I = N
2I = 32
I = 5
На странице 3000 знаков, тогда объем информации = 3000 * 5 = 15000 бит.

Двоичный алфавит
А что если алфавит состоит только из двух символов 0 и 1?
В этом случае: N = 2; 2I = N; 2I = 2; I = 1!
При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации.
Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания
«binary digit» - «двоичная цифра».

Достаточный алфавит
Удобнее всего измерять информацию, когда размер алфавита N равен целой степени двойки. Например, если N=16, то каждый символ несет 4 бита информации потому, что 24 = 16. А если N =32, то один символ «весит» 5 бит.
Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. С ним мы скоро встретимся при работе с компьютером. Это алфавит мощностью 256 символов. В алфавит такого размера можно поместить все практически необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания....
Поскольку 256 = 28, то один символ этого алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.
1 байт = 8 бит

Количество информации в тексте
Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.
В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах.
Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов.
Значит страница содержит 40x60=2400 байт информации.
Объем всей информации в книге: 2400 х 150 = 360 000 байт.

Более крупные единицы информации

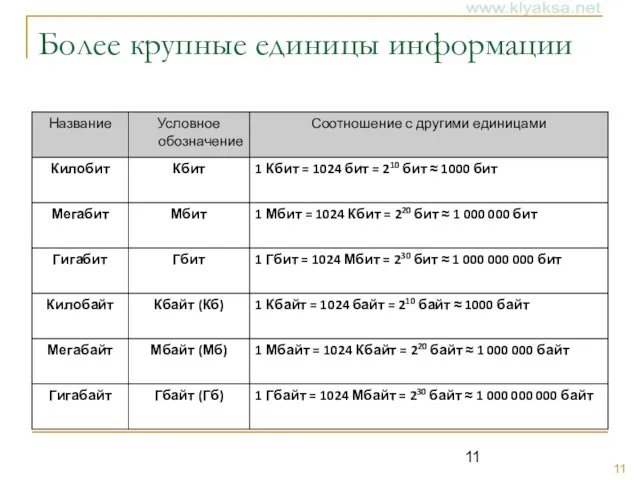
Скорость передачи информации
Прием-передача информации могут происходить с разной скоростью.
Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.
Очевидно, эта скорость выражается в таких единицах, как бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.

Вопросы:
Что такое «алфавит»? Что такое «мощность алфавита»?
Как определяется количество информации в сообщении с алфавитной точки зрения?
Что больше 1 Кбайт или 1000 байт?
Расположите единицы измерения информации в порядке возрастания:
Гигабайт; Байт; Мегабайт; Килобайт.
Сколько информации содержится в сообщении, если для кодирования одного символа использовать 1 байт:
«Компьютер – универсальный прибор.»
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличается количество информации в этих текстах?

Задание 2:
Племя Мумбу-Юмбу использует алфавит из букв: αβγδεζηθλμξσφψ, точки и для разделения слов используется пробел.
Сколько информации несет свод законов племени, если в нем 12 строк и в каждой строке по 20 символов?