Формула полной вероятности, Байес, Бернулли

Проверочное задание.
Вероятности того, что произвольная деталь окажется бракованной в результате предварительных механической и термической обработки, равны соответственно 0,25 и 0,2. Вероятности, что этот брак можно устранить путем дополнительной обработки, соответственно равны 0,6 и 0,5. Если событие А – деталь окажется бракованной в результате предварительной механической обработки,

событие В – деталь окажется бракованной в результате предварительной термической обработки, а событие C – деталь после предварительной обработки имеет устранимый брак, то верным является соотношение …
1.
2.
3.
4.
Ответ: пункт 2

2. Задание.
Пусть p – вероятность того, что хотя бы одна из трех случайно взятых после предварительной обработки деталей будет иметь неустранимый брак, тогда значение выражения 1000 p равно …
Ответ: 488,
так как 1- (0.25 × 0.6 + 0.2 × 0.5 + 0.55)3 = 1 -
- 0.512=0.488

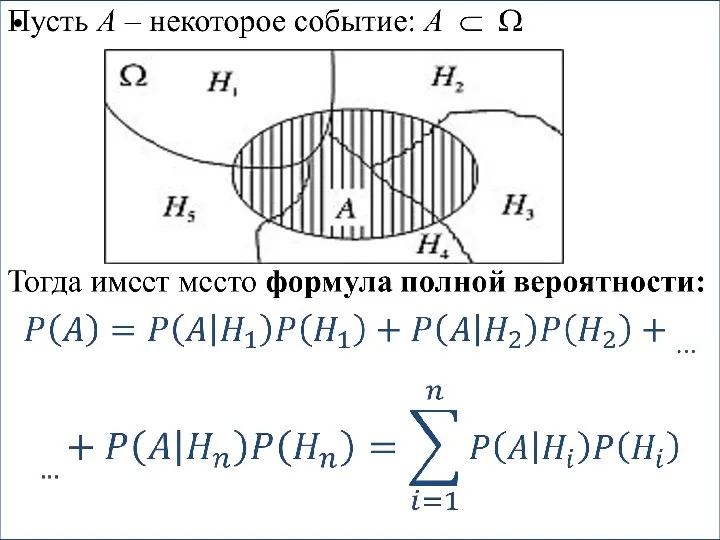
Формула полной вероятности
Часто при решении простых задач теории вероятностей формально не вводят вероятностное пространство, а сразу выделяют полную группу случайных событий (условий), вероятности которых легко определить из условий задачи и вероятность интересующего события находят по формуле полной вероятности.

Пусть имеется группа событий Н1, Н2,..., Нn, обладающая следующими свойствами:
1) все события попарно несовместны: Нi ∩ Нj = Ø; i, j = 1, 2, ..., n; i ≠ j;
2) их объединение образует пространство элементарных исходов Ω:
Ω = Н1 U Н2 U ... U Нn
В этом случае H1, H2,..., Hn образуют полную группу событий.

Пример. В магазине продаются электролампы производства трех заводов, причем доля первого завода - 30%, второго - 50%, третьего - 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность, что случайно выбранная в магазине лампа оказалась бракованной.
Решение: Пусть событие H1 состоит в том, что выбранная лампа произведена на первом заводе, H2 на втором, H3 - на третьем заводе.
Очевидно:
P(H1) = 3/10, P(H2) = 5/10, P(H3) = 2/10.

Пример: В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара. После того, как шары во второй урне перемешались, из неё выкатился шар. Найти вероятность того, что выкатившийся из второй урны шар белый.
Решение: Пусть событие Н1 – из первой урны во вторую перекатились два белых шара, событие Н2 -два чёрных шара, событие Н3 - шары разного цвета. Вычислим вероятности:

Пример:
Три экзаменатора принимают экзамен у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, третий — 21 студента (выбор студентов производят из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у 1-го преподавателя равны 40%, у 2-го — только 10%, у 3-го — 70%. Найти вероятность, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим гипотезы H1; H2; H3; состоящие в том, что слабо подготовившийся студент отвечал 1-му, 2-му и 3-му экзаменатору соответственно. По условию:
Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда по условию задачи
По формуле полной вероятности:

Пример. В составе Думы представлены 3 партии (по 100, 150, 50 человек от 1-й, 2-й и 3-й партий соответственно). Кандидата на должность спикера Думы поддерживают 50% представителей первой партии, 70% - второй и 10% - третьей партии. Какова вероятность, что наудачу выбранный член Думы поддерживает выдвинутую кандидатуру на должность спикера?
Решение: Пусть событие A={наудачу выбранный представитель думы поддерживает выдвинутую кандидатуру}

С событием А тесно связаны гипотезы:
Н1 - {выбранное лицо представляет 1-ую партию}; Н2 - {выбранное лицо представляет 2-ую партию}; Н3 - {выбранное лицо представляет 3-ю партию}. Вероятности гипотез определяются из условия:
Условные вероятности события А даны в условии:

В группе спортсменов лыжников в 2 раза больше, чем бегунов, а бегунов в 3 раза больше, чем велосипедистов.
Вероятность выполнить норму для лыжника 0,9, для бегуна 0,75, для велосипедиста - 0,8.
Найти вероятность того, что спортсмен, выбранный наугад, выполнит норму.

Теорема Байеса — одна из основных теорем теории вероятностей, определяющая вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях.
По ф. Байеса можно более точно пересчитывать вероятность, беря в учёт как ранее известную информацию, так и данные новых наблюдений.
То́мас Ба́йес (Бейес) (1702 — 1761) — английский математик и священник, член Лондонского королевского общества.

Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность, что оно было вызвано данной причиной. События, отражающие действие «причин», наз. гипотезы — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы наз. априорной (насколько вероятна причина вообще), условную - с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии).

Формула полной вероятности является просто следствием свойства счетной аддитивности вероятности и ее применение часто означает, что мы неявно строим вероятностное пространство. Формула Байеса действительно расчетная – для ее применения требуется , чтобы вероятностное пространство уже было определено.

Пример.
Бригада, работающая в дневную смену, производит изделий в 2 раза больше, чем работающая в ночную. Отсюда следует, что если выбрать случайным образом изделие, произведённое в цеху, то с вероятностью 2/3 ≈ 0,66 оно произведено бригадой, работающей днём. Это априорная вероятность.
Известно, что бригада, работающая днём, производит 3% некондиционных изделий, а работающая ночью, – 7% некондиции.

Пусть случайным образом отобранное изделие оказалось некондиционным. Тогда по формуле Байеса вычислим апостериорную вероятность, что это изделие произведено дневной бригадой
P(Н1/А) = (3/100)·(2/3)/((3/100)·(2/3) +
+ (7/100)·(1/3)) ≈ 0,632
Как видно, апостериорная вероятность интересующего нас события несколько ниже априорной вероятности.

Пример. В ящике содержатся 20 деталей, изготовленных на заводе № 1; 30 деталей, изготовленных на заводе № 2; 50 деталей, изготовленных на заводе № 3. Вероятность, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,8; на заводе № 2 – равна 0,7, на заводе № 3 – равна 0,9. Тогда вероятность, что наудачу извлеченная деталь окажется отличного качества, равна …
Решение: Для вычисления вероятности события A (наудачу извлеченная деталь окажется отличного

Задача. В первой урне 7 белых и 3 черных шара. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
Варианты ответов:
3/4 2) 3/5
3) 1/4 4) 9/10

Задание: Для проверки усвоения материала случайным образом выбран студент. В группе 6 отличников, 7 хорошистов и 3 средних студента. Отличник справляется с тестом с вероятностью 0,85, хорошист - 0,6, а средний студент 0,3.
Вычислить вероятность:
а) априорную вероятность, что был протестирован хороший студент;
в) что студент не справился с тестом;
с) что был выбран хороший студент, если известно, что студент с тестом не справился.