Содержание
- 2. ЗАМЕНИТЕ ЗНАКИ * ОДНОЧЛЕНАМИ ТАК, ЧТОБЫ ВЫПОЛНЯЛОСЬ РАВЕНСТВО 1) (6а5 + * )2 = * +
- 3. Примеры (* + 2х2)2= 9у6 + * + * Вместо первой звёздочки поставим 3у2, так как
- 4. Ответы 1) 5х, 36а10, 60а5х; 6m2n3, 100m10, 120m7n3; 5x2y, 40x9y, 16x14; 7a4b3, 64a6, 112a7b3. Следующее задание
- 5. ЗАМЕНИТЕ ЗНАКИ * ОДНОЧЛЕНАМИ ТАК, ЧТОБЫ ВЫПОЛНЯЛОСЬ РАВЕНСТВО 1) ( * - * )2 = *
- 6. Примеры (* + 2х2)2= 9у6 + * + * Вместо первой звёздочки поставим 3у2, так как
- 7. Ответы 1) 5b3, 7c, 25b6; 9x, 10x2y3, 18x3y3; 7x3, 5y2, 49x6, 25y4; 8c5, 3d3, 64c10, 9d3.
- 8. РАСКРОЙТЕ СКОБКИ 1) (х2 + 1)2; 2) (2у3 – 6)2; 3) (4х4 + q)2; 4) (5m3
- 9. ПРАВИЛА И ПРИМЕРЫ Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого на
- 10. Ответы 1) x4 + 2x2 + 1; 2) 4y6 - 24y3 + 36; 3) 16x8 +
- 11. ИСПОЛЬЗУЯ ФОРМУЛЫ КВАДРАТА СУММЫ И КВАДРАТА РАЗНОСТИ, ВЫЧИСЛИТЕ 1) 792; 2) 212; 3) 882; 4) 982.
- 12. Примеры 232=(20+3)2=202+2·20·3+32=400+120+9=529 492=(50-1)2=502-2·50·1+12=2500-100+1=2401 Чтобы возвести в квадрат число, которое оканчивается на 5, достаточно перемножить число, составленное
- 13. Ответы (80-1)2 =6400-160+1= 6241; (20+1)2=400+40+1= 441; (90-2)2=8100-360+4=7744; (100-2)2=10000-400+4=9604. Работа завершена
- 15. Скачать презентацию












 Соленая рыба
Соленая рыба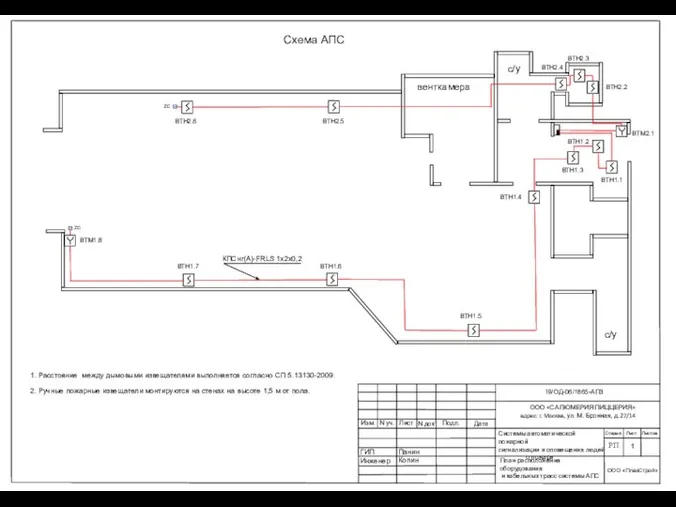 Схема АПС
Схема АПС Абсолютные и относительные статистические показатели
Абсолютные и относительные статистические показатели  Культура: понятие и сущность
Культура: понятие и сущность ИСПАРЕНИЕ ВЛАГИ ПОД ДЕЙСТВИЕМ СОЛНЦА
ИСПАРЕНИЕ ВЛАГИ ПОД ДЕЙСТВИЕМ СОЛНЦА МикротурбинаMTI 250
МикротурбинаMTI 250 Презентация на тему Двадцать четвёртое февраля
Презентация на тему Двадцать четвёртое февраля  Фотоальбом. От проекта до эксплуатации
Фотоальбом. От проекта до эксплуатации Запуск рекламы
Запуск рекламы Презентация команды АО МНИИТЭП
Презентация команды АО МНИИТЭП Особенности кожного покрова
Особенности кожного покрова презентация сайт
презентация сайт Новый человек в новых медиа
Новый человек в новых медиа Государственное управление в космической отрасли
Государственное управление в космической отрасли Презентация на тему Периметр и площадь прямоугольника
Презентация на тему Периметр и площадь прямоугольника  Играем и читаем
Играем и читаем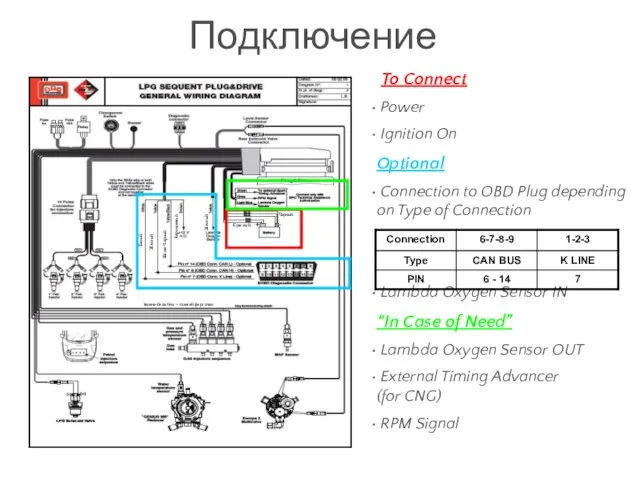 Подключение
Подключение Индивидуальное предпринимательство
Индивидуальное предпринимательство IP-система iPOLIS Samsung
IP-система iPOLIS Samsung Diagonal elements
Diagonal elements 1
1 Тиамин
Тиамин Основные фонды предприятия
Основные фонды предприятия Базовая сердечно-легочная реанимация
Базовая сердечно-легочная реанимация  Независимая оценка качества образования. Этапы формирования 1-х классов
Независимая оценка качества образования. Этапы формирования 1-х классов Использование параллелограмма в жизни
Использование параллелограмма в жизни координаты
координаты Регулирующая и надзорная деятельность банка России
Регулирующая и надзорная деятельность банка России