fp3

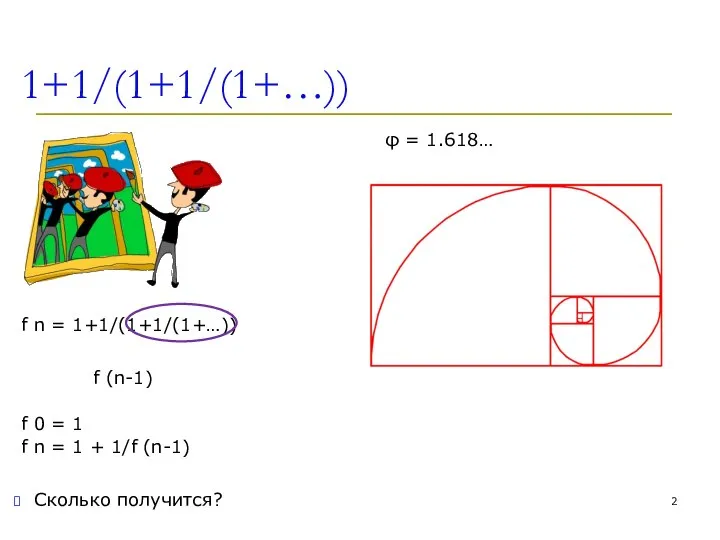
1+1/(1+1/(1+…))
f n = 1+1/(1+1/(1+…))
f (n-1)
f 0 = 1
f n = 1 + 1/f (n-1)
Сколько получится?
φ = 1.618…

Золотое сечение
Такой предмет у вас в сумке?

0+1/(1+1/(2+1/3+…))
b n = 0+1/(1+1/(2+1/3+…))
При трудностях помогает доп.параметр
b’ k n = k+1/(k+1+1/(...+1/n)))
b n = b' 0 n
b' k n = if (k == n)
then n
else k + 1 / b' (k+1) n

sumsin
sin(1+2+...+n)/(sin 1+sin 2+...+sin n)
Накапливающие параметры
s1 s2
0 0
1 sin 1
1+2 sin 1 + sin 2
1+2+3 sin 1 + sin 2 + sin 3
…
sumsin n = sumsin' n 0 0
sumsin' 0 s1 s2 = sin s1 / s2
sumsin' n s1 s2 = sumsin' (n-1) (s1+n) (s2+sin n)
s1 ? s1+n
s2 ? s2+sin n

sumfact
1!+2!+3!+…+n!
Желательно O(n)
i p s
1 1 0
2 1 1
3 1*2 1+1*2
4 1*2*3 1+1*2+1*2*3
5 1*2*3*4 1+1*2+1*2*3+1*2*3*4
sumfact n = sumfact' n 1 1 0
sumfact' 0 i p s = s
sumfact' n i p s = sumfact' (n-1) (i+1) (p*i) (s+p*i)
i ? i+1
p ? p*i
s ? s+p*i

Еще синтаксис

Безымянная переменная (wildcard)
sumfact' 0 i p s = s
Лучше так:
sumfact' 0 _ _ s = s
_ - безымянная переменная (wildcard)
Только слева от =
с
с

let
sumfact' n i p s = sumfact' (n-1) (i+1) (p*i) (s+p*i) Еще одна проблема (небольшая в данном случае)
p*i – два раза
DRY (Don’t Repeat Yourself)
sumfact' n i p s = let p’ = p*i
in sumfact' (n-1) (i+1) p’ (s+p’)
с
с

let в общем случае
Двумерный синтаксис
let
правило1
правило2
…
in выражение
Могут быть и правила с параметрами
М.б. частью выражения
f n = 1 + let
i = 55
j = n*n +
5* n + 8
g k = k * j
in g n * 2
Где кончается правило и начинается следующее?
Двумерный синтаксис
(off-side rule)
Запоминаем позицию первой лексемы после let (i в примере)
Правее ? продолжение правила
На том же уровне ? новое правило
Левее ? конец конструкции

Явное задание синтаксиса
let
правило1
правило2
…
in выражение
Можно использовать { ; }, тогда отступы не имеют значение
let {правило1; правило2; правило3} in выражение

where
sumfact' n i p s = sumfact' (n-1) (i+1) p’ (s+p’) where p’ = p*i
левая часть = правая часть
where вспомогательные определения
Разница:
let можно писать где угодно
where – часть правила
Тоже двумерный синтаксис

Еще д.з.

minlist
Не совсем правильное решение
minlist [x] = x
minlist (x:xs) = if x < minlist xs
then x
else minlist xs
minlist [1..100] – очень долго
Правильное решение 2
minlist [x] = x
minlist (x:xs) =
let m = minlist xs
in if x < m then x else m
Правильное решение 3
Используем min
minlist [x] = x
minlist (x:xs) =
min x (minlist xs)

minlist – c чего начать?
С чего начать?
minlist [x] = x
или
minlist [] = очень большое число
minlist [] = 1/0
Вам что больше нравится?
За minlist [] = 1/0
В более сложных случаях (минимум четных чисел)
За minlist [x] = x
Работает не только для чисел
minlist [“klm”, “abc”, “pqr”]
? "abc"

minsum
minsum [_] = 1/0
minsum (x:y:xs) = min (x+y) (minsum (y:xs))

rev
Вариант 1, используя ++ [x]
rev [] = []
rev (x:xs) = rev xs ++ [x]
Медленно…
Вариант 3, быстрый (O(n))
rev xs = rev’ xs []
rev’ [] ys = ys
rev‘ (x:xs) ys = rev’ xs (x:ys)
Прием:
Накапливающий параметр

Забыл сказать
length – длина списка
length [] = 0
length (_:xs) = 1 + length xs
Строки – списки символов
"abc" – сокращенная запись для [‘a’, ‘b’, ‘c’]
"abc" ++ "klm" ? "abcklm"
head "abc" ? 'a'
length "abc" ? 3

Кортежи

Кортежи (tuples)
(1,2) - пары
(3,7,11) – тройки
(3, 4, 88, 9) и т.д.
Для пар есть встроенные функции fst и snd
fst (x, _) = x
sdn (_, y) = y
Обычно обрабатываем с помощью сопоставления с образцом
abs (x, y) = sqrt (x*x+y*y)
В чем разница со списками?
Значения могут быть разных типов
("Сидоров“, 1990, 178, 4.7, True)
Нельзя организовать цикл по всем элементам набора

zip
zip – соединить два списка в список пар
zip [1,2,3] [33,55,22] ?
[(1,33), (2,55), (3,22)]
Разной длины ? укорачиваем
zip (x:xs) (y:ys) =
(x,y) : zip xs ys
zip [] _ = []
zip _ [] = []
Или
zip _ _ = []

Pattern binding
Пусть функция возвращает пару:
areaPerim r = (3.14*r^2, 2*3.14*r)
areaPerim 10 ? (314, 62.8)
Как получить результат?
fst и snd:
let res = areaPerim 10
in fst res / snd res
Слева от = м.б. шаблон:
let (s, p) = areaPerim 10
in s / p
И в лямбда-выражениях: слева от -> могут быть шаблоны
map (\(x, y) -> x+y)) xs
[(1,2), (3,4)]
? [3, 7]
Похожая вещь в С++:
tie
tie(s, p) = areaPerim(10);

Алгебраические типы данных

Как называются стандартные типы?
Integer, Char, Bool, Double
Списки
[Integer]
Строка
String – сокращение для [Char]
Кортежи
(Integer, String)

data – простой случай.
Конструкторы
data Point = Pt Integer Integer
Pt 33 50
Похоже на структуры в обычных языках
Для доступа к полям – pattern matching
abs (Pt x y) = sqrt (x^2+y^2)
Можно определить и именованные поля
Pt – конструктор
Совсем не то, что конструктор в обычных языках ☹
Задается в data
Может использоваться в pattern matching
Начинается с заглавной буквы
Имя может совпадать с именем data:
data Point = Point Integer Integer

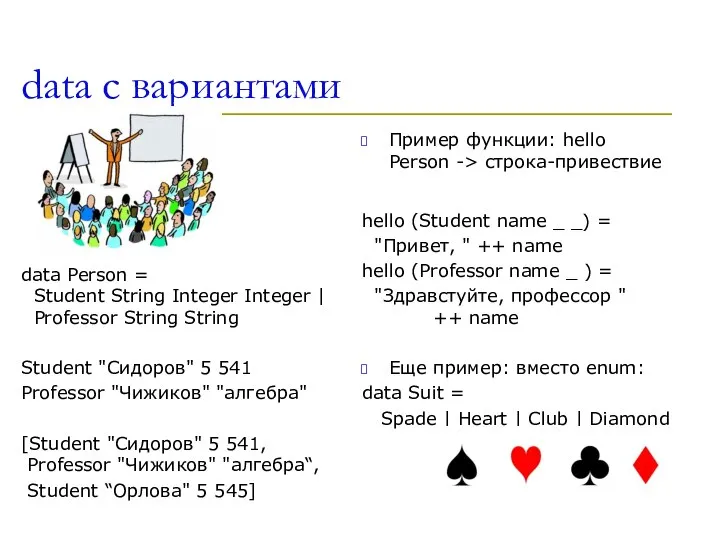
data c вариантами
data Person = Student String Integer Integer |
Professor String String
Student "Сидоров" 5 541
Professor "Чижиков" "алгебра"
[Student "Сидоров" 5 541, Professor "Чижиков" "алгебра“,
Student “Орлова" 5 545]
Пример функции: hello
Person -> строка-привествие
hello (Student name _ _) =
"Привет, " ++ name
hello (Professor name _ ) =
"Здравстуйте, профессор " ++ name
Еще пример: вместо enum:
data Suit =
Spade | Heart | Club | Diamond

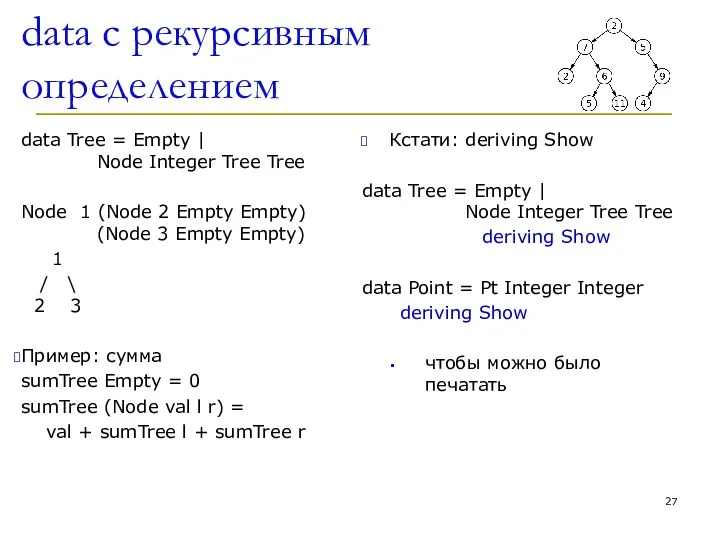
data c рекурсивным
определением
data Tree = Empty | Node Integer Tree Tree
Node 1 (Node 2 Empty Empty)
(Node 3 Empty Empty)
1
/ \
2 3
Пример: сумма
sumTree Empty = 0
sumTree (Node val l r) =
val + sumTree l + sumTree r
Кстати: deriving Show
data Tree = Empty | Node Integer Tree Tree
deriving Show
data Point = Pt Integer Integer
deriving Show
чтобы можно было печатать

Снова про функции высшего порядка

check
check cond [] = False
check cond (x:xs) =
if cond x then True
else check cond xs
Примеры вызова:
check (\x -> x * x <= 100) xs
mycond x = x*x < 100
check mycond xs
check mycond xs where
mycond x = x*x < 100
Еще вариант
check cond [] = False
check cond (x:xs) = cond x || check cond xs

Стандартные функции all и any
any - проверить, что хотя бы один элемент удовлетворяет условию
any (\x->x>0) [5,-1,8] ? True
all – проверить, что все элементы удовлетворяют условию
all (\x->x>0) [5,-1,8] ? False

checkDifferent
checkDifferent [] = True
checkDifferent (x:xs) =
if x содержится в xs
then False
else checkDifferent xs
x содержится в xs:
check (\t -> t == x) xs
Или any(\t->t==x)
checkDifferent (x:xs) =
if any(\t -> t == x) xs
then False
else checkDifferent xs
Стиль Haskell!!
(использовать функции высшего порядка)
Еще вариант, без if
checkDifferent (x:xs) =
not any (\t -> t == x) xs &&
checkDifferent xs
Более эффективное рещение?
N Log N
Например, сначала отсортировать

Частичная параметризация
Задача 1: Написать функцию для вычисления квадратного трехчлена
f a b с x = a*x^2 + b*x + c
Задача 2: Ко всем элементам списка применить функцию x^2+2*x+4
Простой способ:
map (\x -> f 1 2 4 x) xs
Частичная параметрзация
map (f 1 2 4) xs
Можно задавать часть параметров (только несколько первых)
Получается функция от оставшихся параметров
f 1 2 4 – функция от x
f 1 2 – функция от с и x
f 1 – функция от b, c и x
Можно использовать при определении функции
f1 = f 1 2 4