Функции у = х2 и у = х3 и их графики

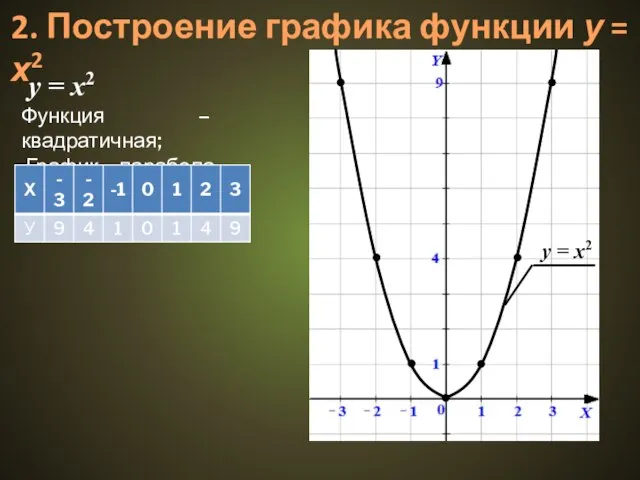
1. Функция у = х2 и её график
9
4
2,25
4
1
1
0
0,25
Свойства функции у = x2:
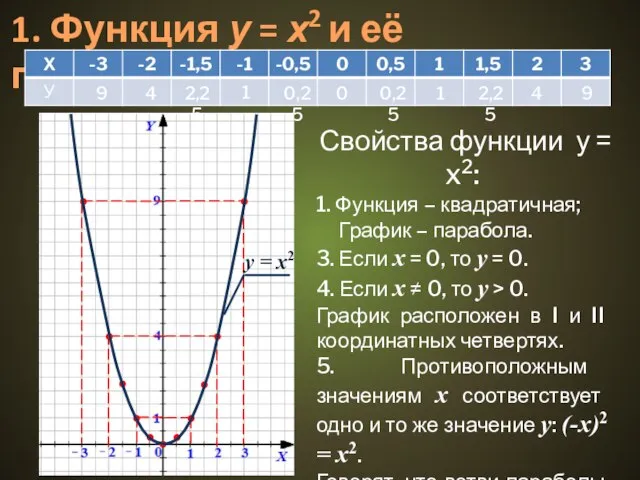
1. Функция – квадратичная;
График – парабола.
3. Если х = 0, то у = 0.
4. Если х ≠ 0, то y > 0.
График расположен в I и II координатных четвертях.
5. Противоположным значениям х соответствует одно и то же значение у: (-х)2 = х2.
Говорят, что ветви параболы симметричны относительно оси ОУ.
9
2,25
0,25
y = x2

2. Построение графика функции у = х2
у = x2
Функция – квадратичная; График – парабола.
y = x2

3. Функция у = х3 и её график
-8
-3,4
-1
3,4
-0,1
0,1
0
Свойства функции у = x3:
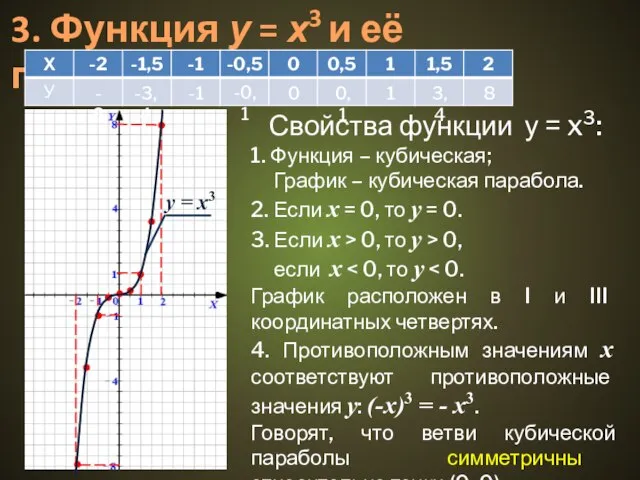
1. Функция – кубическая;
График – кубическая парабола.
2. Если х = 0, то у = 0.
3. Если х > 0, то y > 0,
если х < 0, то y < 0.
График расположен в I и III координатных четвертях.
4. Противоположным значениям х соответствуют противоположные значения у: (-х)3 = - х3.
Говорят, что ветви кубической параболы симметричны относительно точки (0; 0).
8
1
y = x3