Функциональные схемы

Функциональные элементы (вентили)
Электронное устройство, получая значение истинности отдельных простых высказываний (1 – наличие сигнала, 0 – отсутствие) могут выдавать значения истинности конъюнкции, дизъюнкции, отрицания. Эти электронные схемы называют функциональными элементами (вентили).

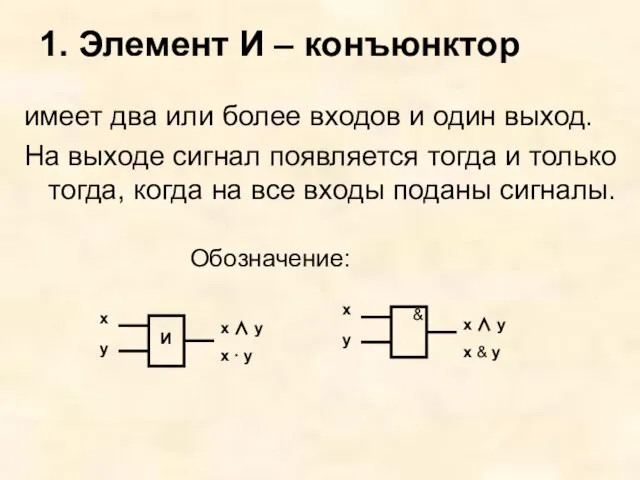
1. Элемент И – конъюнктор
имеет два или более входов и один выход.
На выходе сигнал появляется тогда и только тогда, когда на все входы поданы сигналы.
х ∧ у
х · у
Обозначение:

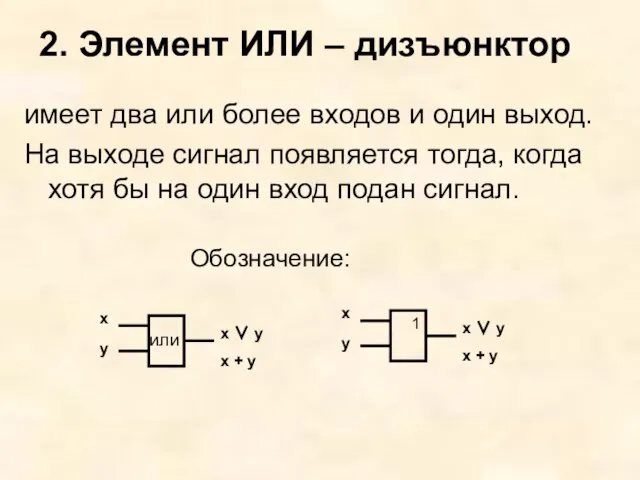
2. Элемент ИЛИ – дизъюнктор
имеет два или более входов и один выход.
На выходе сигнал появляется тогда, когда хотя бы на один вход подан сигнал.
Обозначение:

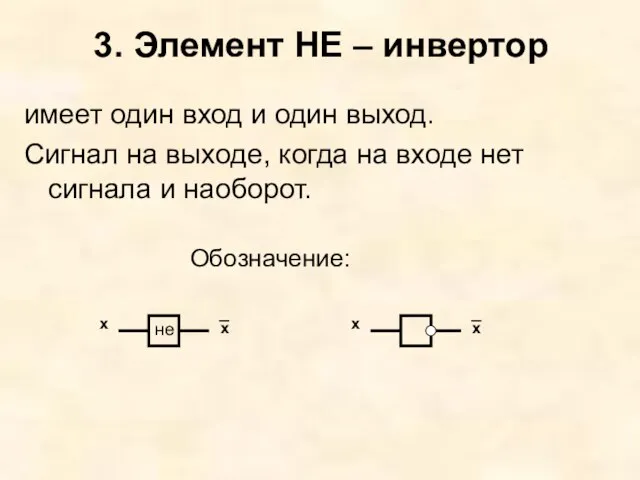
3. Элемент НЕ – инвертор
имеет один вход и один выход.
Сигнал на выходе, когда на входе нет сигнала и наоборот.
Обозначение:

Из функциональных элементов, соединяя их между собой можно составлять функциональные схемы, реализующие сложные логические формулы. Каждой логической формуле можно поставить в соответствие функциональную схему.
Например:

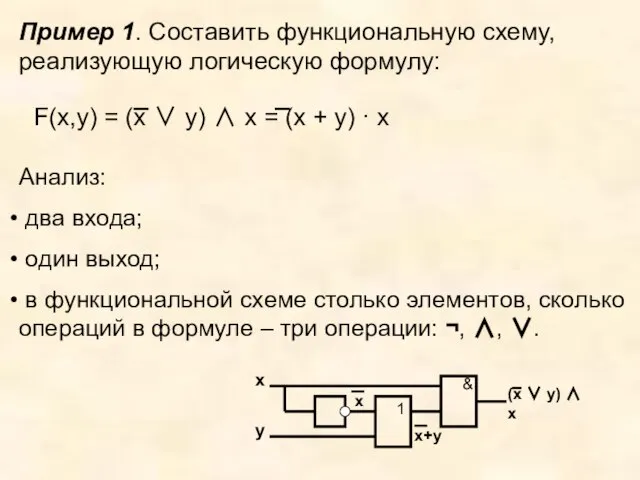
Пример 1. Составить функциональную схему, реализующую логическую формулу:
Анализ:
два входа;
один выход; в функциональной схеме столько элементов, сколько операций в формуле – три операции: ¬, ∧, ∨.

Задание: составить функциональную схему, реализующую логическую высказывание:
«Я обязательно поеду на футбольный матч, если достану билет или меня пригласит товарищ и если не будет дождя».

Пример 1. Условия работы будущей схемы заданы таблицей истинности:

Синтез функциональной схемы одноразрядного двоичного сумматора на два входа
0
0
+
0
0
1
+
1
1
0
+
1
1
1
+
10
X
Y
+
PS
В общем виде:
Х, Y – входы:
S – соответствует значению суммы в данном разряде;
Р – перенос в старший разряд.
Условия работы будущей схемы заключим в таблицу истинности:
X
Y
+
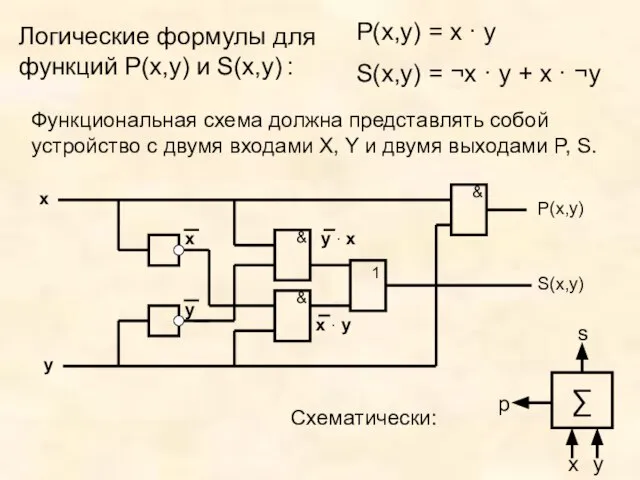
PS

Логические формулы для функций P(x,y) и S(x,y) :
P(x,y) = x · y
S(x,y) = ¬x · y + x · ¬y
Функциональная схема должна представлять собой устройство с двумя входами X, Y и двумя выходами P, S.
Схематически:

Сконструированный двоичный сумматор может быть использован лишь в разряде единиц – нет третьего входа для единицы переноса из младшего разряда.
Для сложения в следующих разрядах нужны сумматоры на три входа.

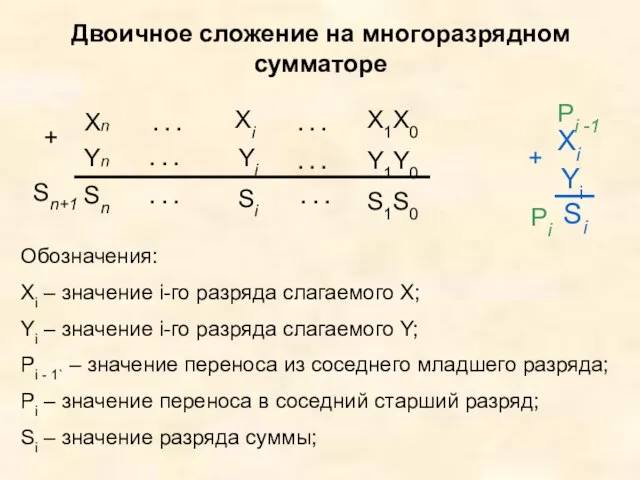
Двоичное сложение на многоразрядном сумматоре
+
Обозначения:
Xi – значение i-го разряда слагаемого Х;
Yi – значение i-го разряда слагаемого Y;
Pi - 1` – значение переноса из соседнего младшего разряда;
Pi – значение переноса в соседний старший разряд;
Si – значение разряда суммы;

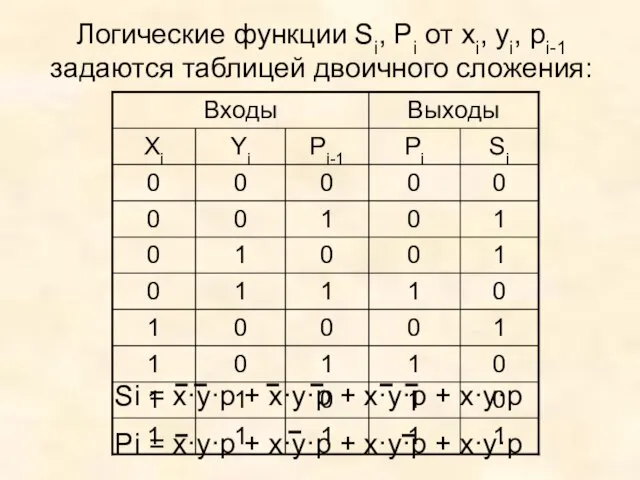
Логические функции Si, Pi от xi, yi, pi-1 задаются таблицей двоичного сложения:

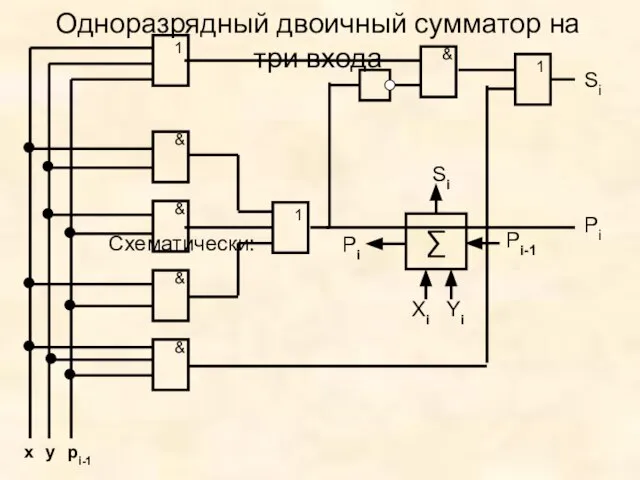
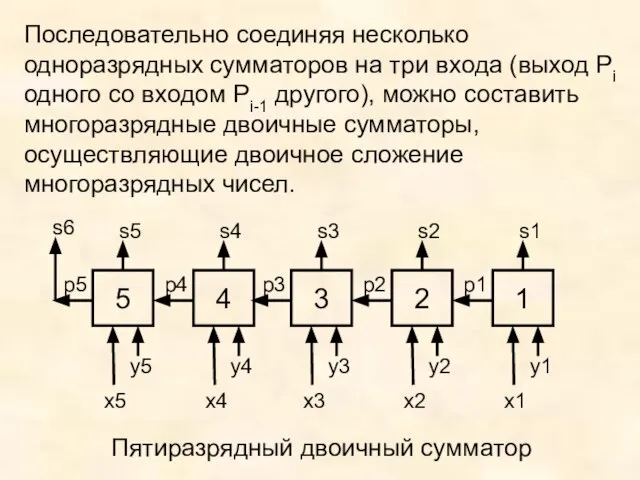
Одноразрядный двоичный сумматор на три входа
Схематически:

Последовательно соединяя несколько одноразрядных сумматоров на три входа (выход Pi одного со входом Pi-1 другого), можно составить многоразрядные двоичные сумматоры, осуществляющие двоичное сложение многоразрядных чисел.
Пятиразрядный двоичный сумматор

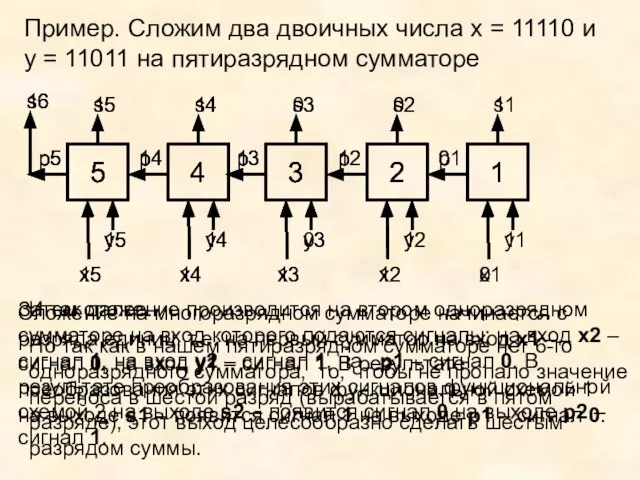
Пример. Сложим два двоичных числа х = 11110 и y = 11011 на пятиразрядном сумматоре
Сложение на многоразрядном сумматоре начинается с разряда единиц, т.е. на первый сумматор на вход х1 – сигнал 0, на вход у1 – сигнал 1. В результате преобразования этих сигналов функциональной схемой 1 на выходе s1 – появится сигнал 1 на выходе р1 – сигнал 0.
Затем сложение производится на втором одноразрядном сумматоре на вход которого подаются сигналы: на вход х2 – сигнал 1, на вход у2 – сигнал 1, на р1 – сигнал 0. В результате преобразования этих сигналов функциональной схемой 2 на выходе s2 – появится сигнал 0 на выходе р2 – сигнал 1.
И так далее.
Но так как в нашем пятиразрядном сумматоре нет 6-го одноразрядного сумматора, то, чтобы не пропало значение переноса в шестой разряд (вырабатывается в пятом разряде), этот выход целесообразно сделать шестым разрядом суммы.