Функция, числовая последовательность

1. Функция
Опр. Заданы два непустых множества Х и Y. Соответствие ƒ, которое каждому элементу х ∈ Х сопоставляет один и только один элемент у ∈ Y, называется функцией и записывается у = f (х), х ∈ Х или
f: Х → Y.

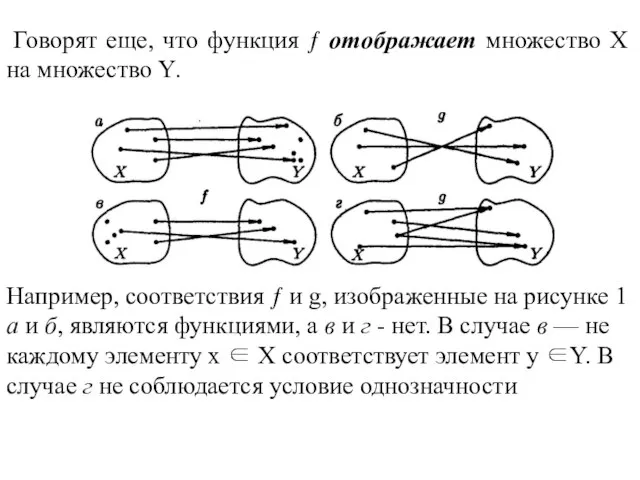
Говорят еще, что функция ƒ отображает множество Х на множество Y.
Например, соответствия ƒ и g, изображенные на рисунке 1 а и б, являются функциями, а в и г - нет. В случае в — не каждому элементу х ∈ Х соответствует элемент у ∈Y. В случае г не соблюдается условие однозначности

Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин x и у говорят, что они находятся в функциональной зависимости.
у = у(х) или у = f(х)
Частное значение функции f (х) при х = а записывают так: ƒ(а). Например, если f (х) = 2x2 - 3, то ƒ(0) = -3, ƒ(2) =5.

Опр. Графиком функции у = f (х) называется множество всех точек плоскости Оху, для каждой из которых х является значением аргумента, a y — соответствующим значением функции.

Три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений
Графический способ: задается график функции.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции.

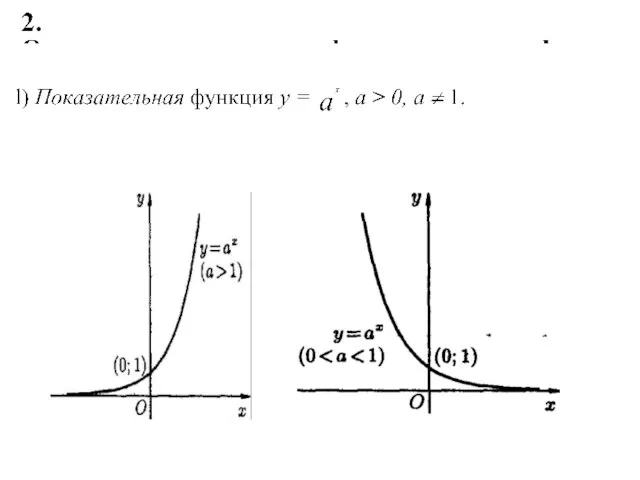
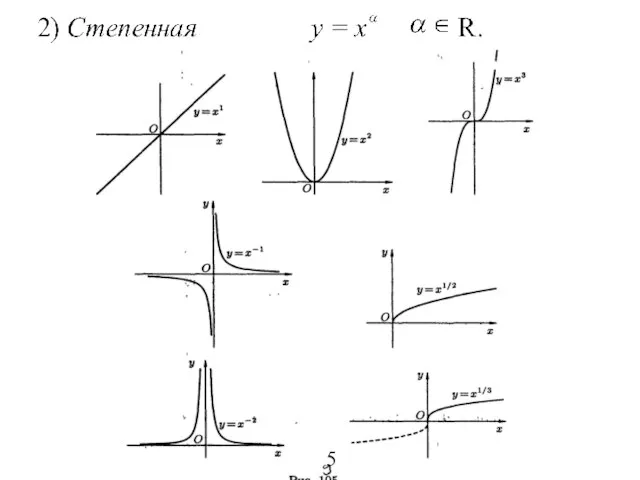
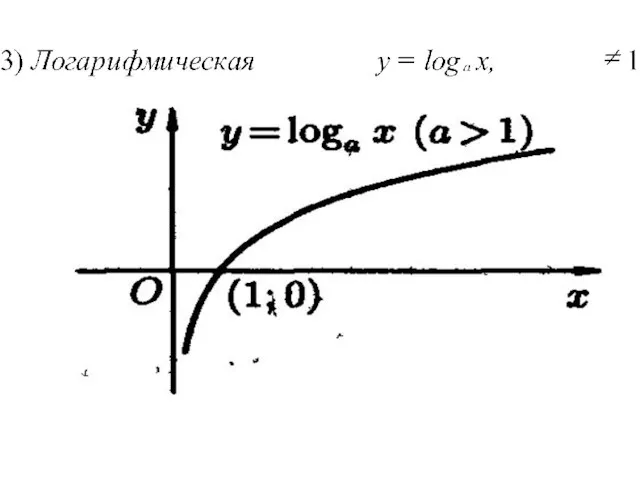
Основные характеристики функции
∙ 1. Функция у = f (х), определенная на множестве D, называется четной, если ∀х ∈ D выполняются условия
-х ∈ D и f (-х) = f (х);
нечетной, если ∀х ∈ D выполняются условия
-х ∈ D и f (-х) = - f (х).
График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.

∙ 2. Пусть функция y=f (x) определена на множестве D. Если для (х1, х2) ∈ D
из х1 < х2 f (x1) < f (x2), то ф-я наз возрастающей на множестве D;
из х1 < х2 f (x1) ≤ ƒ (х2), то ф-я наз неубывающей;
из х1 < х2 ƒ(x1) > f (x2), то ф-я наз убывающей;
из х1 < х2 f(x1) ≥ ƒ(x2), то ф-я наз невозрастающей .
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными.

∙ 3. Функцию у = f (х), х ∈ D, называется ограниченной на D, если ∃М>0: ∀x ∈D ⇒ ⏐f(х)⏐ ≤ М. Отсюда следует, что график ограниченной функции лежит между прямыми у = -М и у = М (см. рис. ).
· 4. Функция у = f (х), определенная на D, называется периодической на этом множестве, если Т > O, что при каждом х ∈ D значение (х+ T) ∈ D и f (х+ T) = f (х). При этом число T называется периодом функции.

5

заданная на множестве N натуральных чисел.
def: {xn} или xп, n ∈ N.
Число х1 называется первым членом (элементом) последовательности, x2 — вторым,..., xп — общим или п-м членом последовательности.
Опр. Под числовой последовательностью х1, х2, хз,…, xп, … понимается функция
хп = f (n),
3. Числовая последовательность и ее предел

υn= n² + 1, zn= , yn = , un = , n∈ N
задают соответственно последовательности
υn={2, 5, 10,..., n² + 1,...}; zn ={-1, 2,-3, 4,..., ,...};
уn={1,,,,…,,…} un={0,,,,,,…,,…}

Опр. Число а называется пределом последовательности {хn}, если для любого положительного числа ε найдется такое натуральное число N, что при всех n > N выполняется неравенство
⏐xn - a⏐ < ε.

Коротко определение предела можно записать так:
(∀ε > 0 ∃ Nε: ∀n > N ε ⇒ ⏐xn – a⏐< ε) ⇔
lim xn = a

Пример Доказать, что
Решение: По определению, число 1 будет пределом последовательности xn= , n ∈ N, если ∀ε > 0 найдется натуральное число N, такое, что для всех n > N выполняется неравенство ⏐ -1⏐< ε, т.е. < ε. Оно справедливо для всех n > , т. е. для всех n > N =[ ] , где [ ] — целая часть числа (целая часть числа х, обозначаемая [х], есть наибольшее целое число, не превосходящее х; так [3] = 3, [5, 2] = 5).
Если ε > l, то в качестве N можно взять [ ] + 1.
Итак, ∀ε > 0 указано соответствующее значение N. Это и доказывает, что

Теорема Если xn=а, yn=b и, начиная с некоторого номера, выполняется неравенство xn ≤ yn, то а ≤ b.