Содержание
- 2. Свойства функции 1.D(y) 2.E(y) 3. Четность функции 4. Периодичность функции 5.Нули функции 6. Наибольшее значение 7.
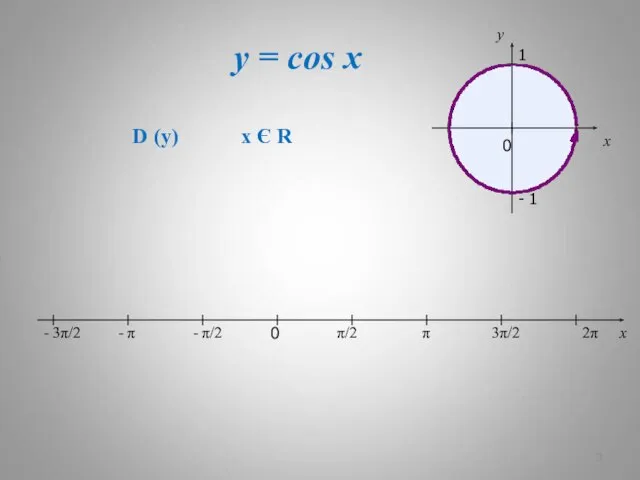
- 3. y = cos x D (y) x Є R
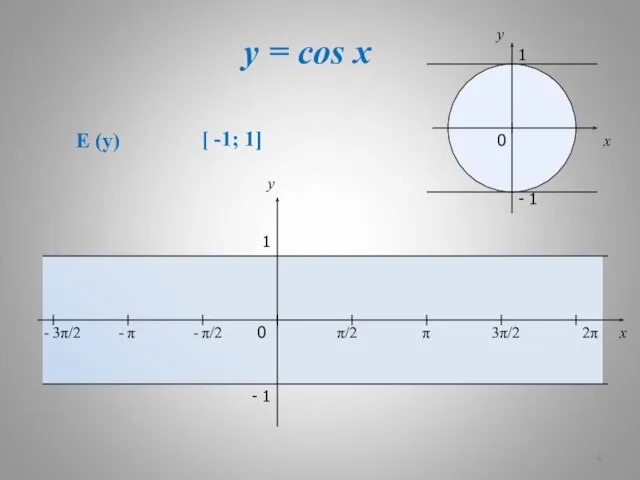
- 4. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 5. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
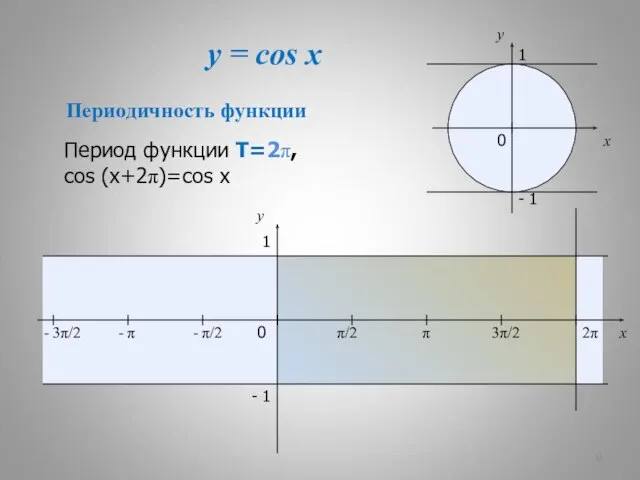
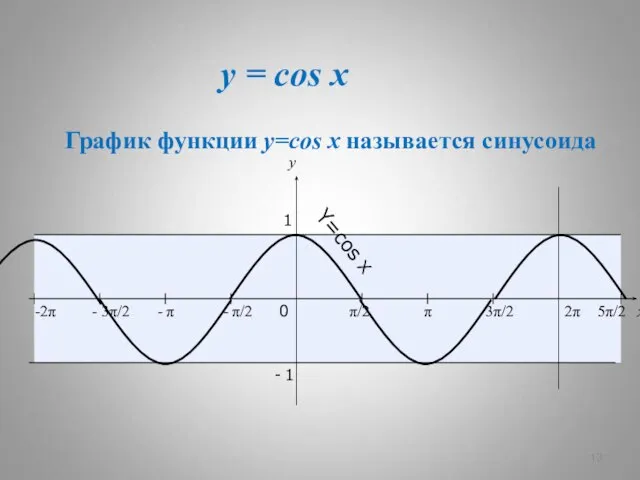
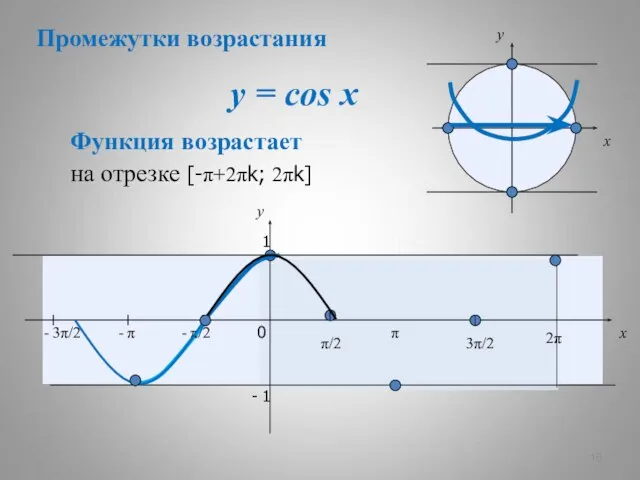
- 6. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
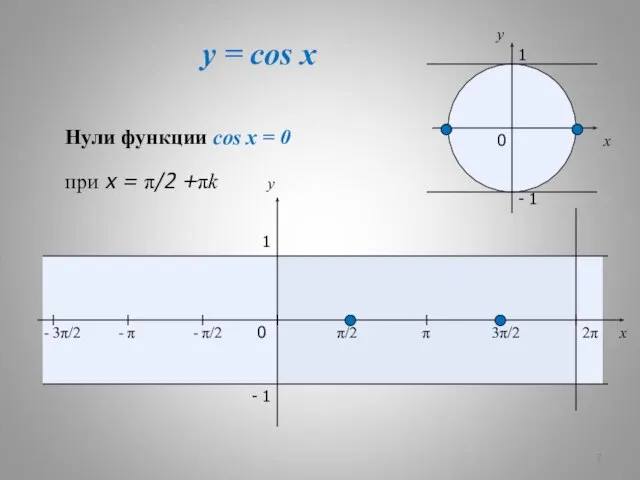
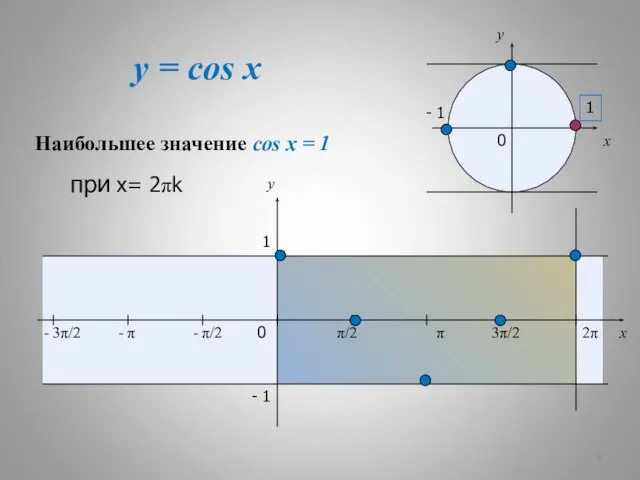
- 7. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
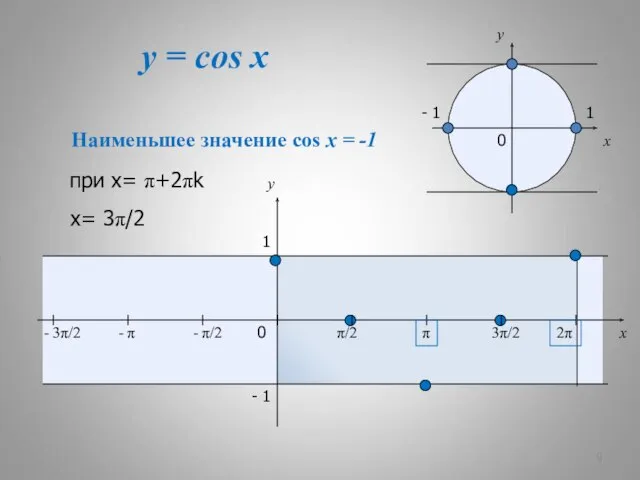
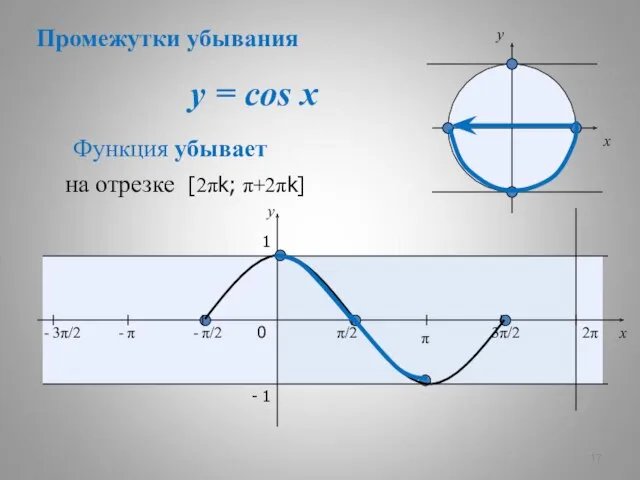
- 8. y = cos x x y 0 π/2 3π/2 2π x y 1 - 1 -
- 9. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
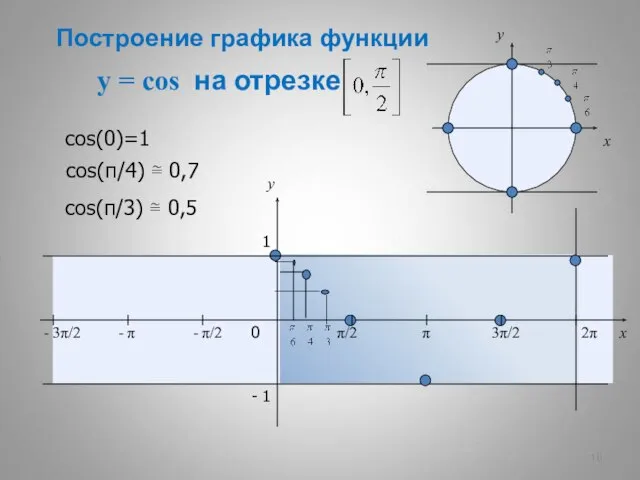
- 10. y = cos на отрезке x y 0 π/2 π 3π/2 2π x y 1 -
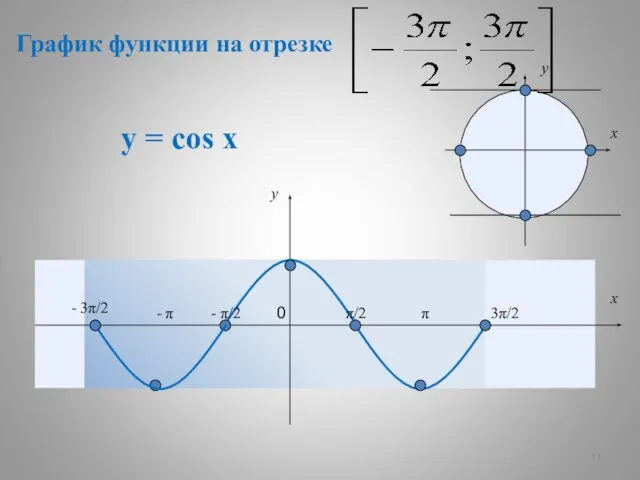
- 11. у = cos x π π/2 - π/2 - π - 3π/2 3π/2 y x 0
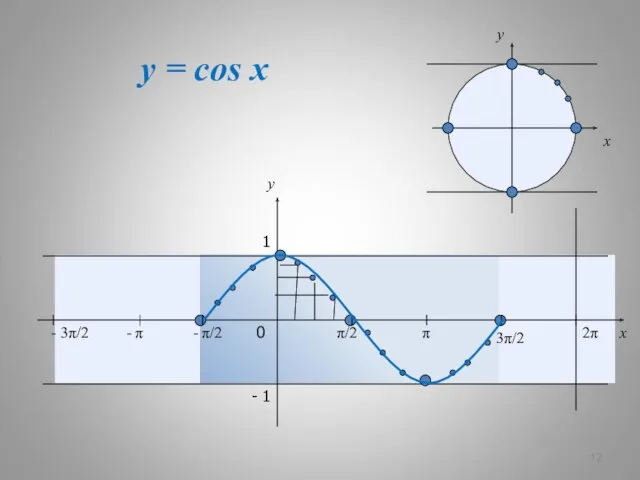
- 12. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 13. y = cos x x y 0 π/2 π 3π/2 2π 1 - 1 - π/2
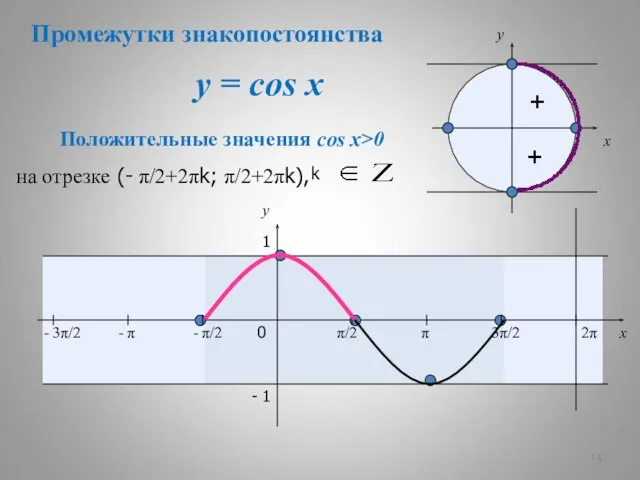
- 14. y = cos x + + x y 0 π/2 π 3π/2 2π x y 1
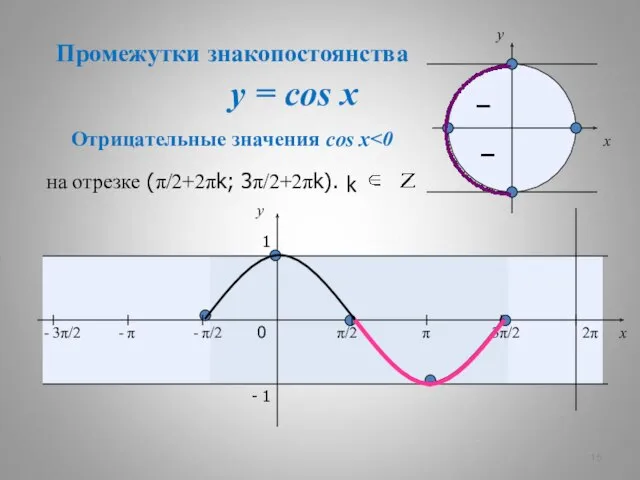
- 15. y = cos x – – x y 0 π/2 π 3π/2 2π x y 1
- 16. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 17. y = cos x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 18. Сравнить числа cos 2 и cos 3 Задача Так как = 3,14, , то Из графика
- 19. Упражнения Пользуясь свойствами функции у = cos x , сравните числа: cos 1000 и cos 1300
- 20. Расположить в порядке возрастания числа cos 1.9 ; cos 3; cos(-1); cos(-1.5). Числа cos 1.9 и
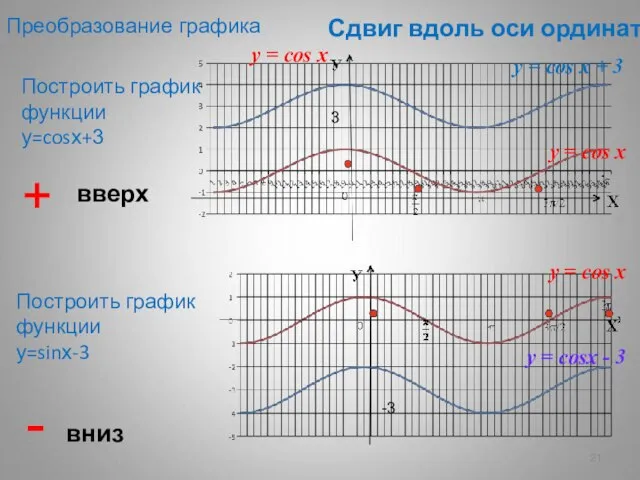
- 21. Сдвиг вдоль оси ординат Построить график функции у=cosх+3 Построить график функции у=sinх-3 + вверх - вниз
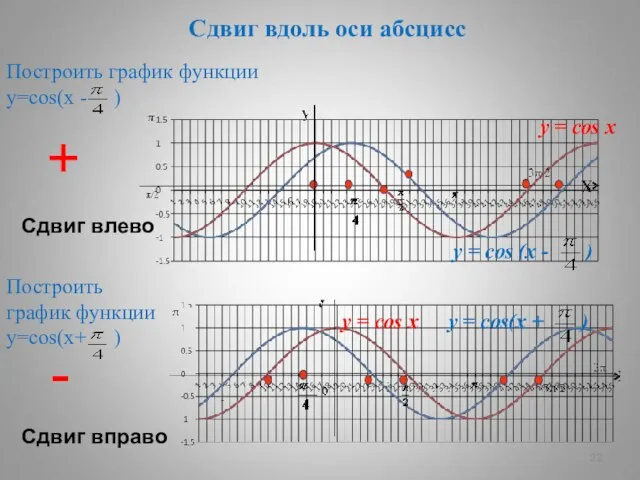
- 22. Сдвиг вдоль оси абсцисс Построить график функции у=cos(х - ) Построить график функции у=cos(х+ ) +
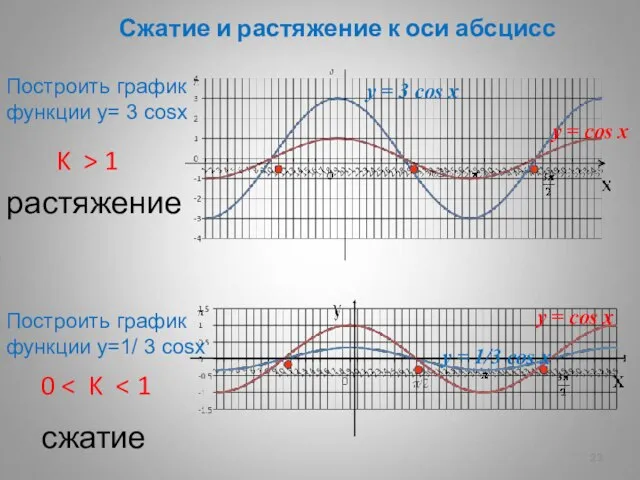
- 23. Сжатие и растяжение к оси абсцисс K > 1 растяжение 0 сжатие Построить график функции у=
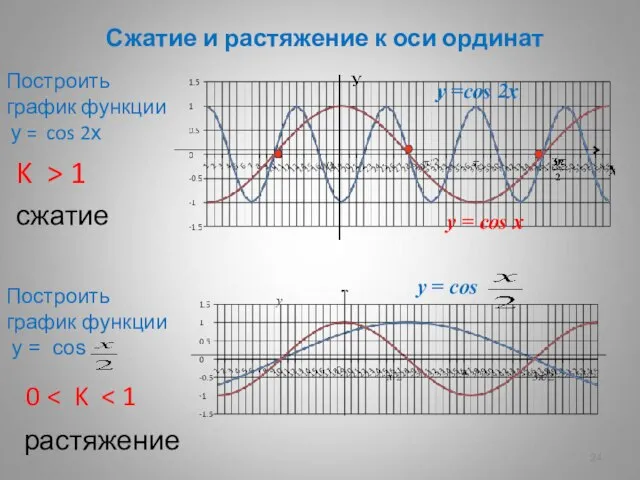
- 24. Сжатие и растяжение к оси ординат Построить график функции у = cos 2х Построить график функции
- 25. У х y = cos x При каких значениях х функция у=cos x принимает значение, равное
- 27. Скачать презентацию






 Второй закон Ньютона
Второй закон Ньютона Political_Correctness
Political_Correctness «Битва за Москву!»
«Битва за Москву!» Страхование имущественных рисков предприятий строительного комплекса
Страхование имущественных рисков предприятий строительного комплекса Презентация на тему Формирование навыков грамотного письма
Презентация на тему Формирование навыков грамотного письма Портфолио учителя татарского языка и литературы
Портфолио учителя татарского языка и литературы Повышение качества знаний по предметам естественно-географического цикла.
Повышение качества знаний по предметам естественно-географического цикла.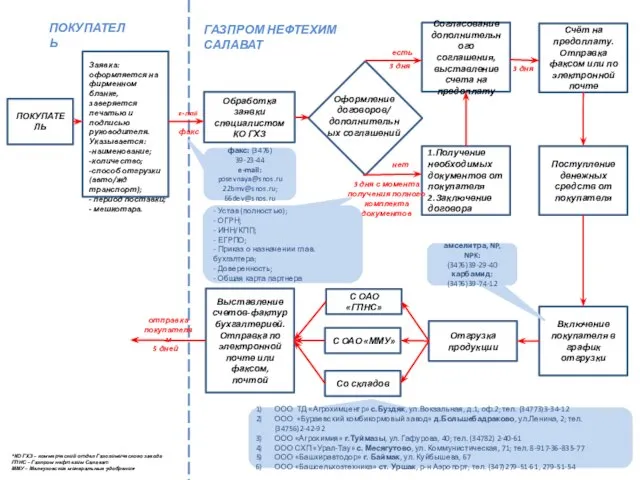 ПОКУПАТЕЛЬ
ПОКУПАТЕЛЬ Система депиляции Skin's
Система депиляции Skin's Гуманитарный факультет
Гуманитарный факультет дискриминация
дискриминация Обстоятельство. Основные Виды обстоятельств
Обстоятельство. Основные Виды обстоятельств Практический опыт развёртывания .NET Forge CMS в Windows Azure. Облачная производительность. Нагрузочные тесты
Практический опыт развёртывания .NET Forge CMS в Windows Azure. Облачная производительность. Нагрузочные тесты Основы конституционного строя РФ
Основы конституционного строя РФ Работа над радостностью
Работа над радостностью Белки. Органические вещества клетки
Белки. Органические вещества клетки Тема: Не будем друг другу чужестранцами!
Тема: Не будем друг другу чужестранцами! Цветочно-декоративное оформление пришкольной территории
Цветочно-декоративное оформление пришкольной территории Творчество Евгения Васильевича Курдакова
Творчество Евгения Васильевича Курдакова Leisure
Leisure Русский портрет. 1 половина. 19 века
Русский портрет. 1 половина. 19 века Герои Второй мировой войны
Герои Второй мировой войны Презентациясоставлена учителем начальных классовМуниципального общеобразовательного учреждения «Средняя общеобразовательна
Презентациясоставлена учителем начальных классовМуниципального общеобразовательного учреждения «Средняя общеобразовательна Сведения и классификация системы управления строительных машин. Конструкция механической системы управления
Сведения и классификация системы управления строительных машин. Конструкция механической системы управления Жанры изобразительного искусства
Жанры изобразительного искусства Litodrill. Водочувствительные глинистые отложения
Litodrill. Водочувствительные глинистые отложения Топография кишечника и операции на нем
Топография кишечника и операции на нем Л. Н. Толстой – человек, мыслитель, писатель
Л. Н. Толстой – человек, мыслитель, писатель