Геометрические сопряжения

Сопряжение прямой и окружности
Сопряжение прямой и окружности будет плавным,если прямая касается окружности.
Точка сопряжения лежит на радиусе, перпендикулярном данной прямой.

Сопряжение двух окружностей
Сопряжение двух окружностей будет плавным, если окружности касаются.
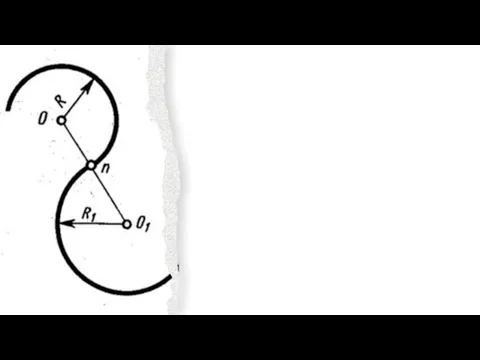
Точка сопряжения лежит на прямой, соединяющей их центры.

Сопряжение двух прямых дугой заданного радиуса.
1.Находят точку О- центр сопряжения. Он должен лежать на расстоянии R от заданных прямых.
2. Находят точки сопряжения. Опускают перпендикуляры из центра сопряжения. Полученные точки являются точками сопряжения.
3. Из центра сопряжения проводят дугу радиуса R между точками сопряжения.

Сопряжение окружности и прямой,дугой заданного радиуса.
Находят центр сопряжения. Для этого из точки О окружности проводят дугу вспомогательной окружности R+ Rс
2. На расстоянии Rс от прямой проводят прямую до пересечения с дугой R+Rс
3. Находят точки сопряжения В и А.
4. Из центра сопряжения т.О проводят дугу радиусом Rс, соединяя ей точки сопряжения В и А.

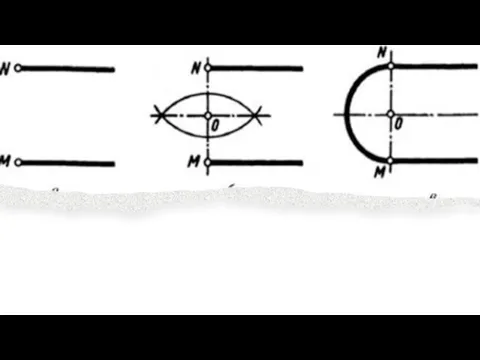
Сопряжение параллельных прямых.

Сопряжение окружностей.