ГЕОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ ЭВОЛЮЦИИ И ВРЕМЕНИ БАЛЛИСТИЧЕСКОГО СУЩЕСТВОВАНИЯ ЭЛЛИПТИЧЕСКИХ ОРБИТ, ИСПЫТЫВАЮЩИХ ГРАВИТАЦИОННО
Содержание
- 2. СОДЕРЖАНИЕ Интегралы для спутникового варианта пространственной ограниченной круговой задачи трех тел Геометрическое исследование интегралов c1, c2
- 3. Интегралы для спутникового варианта пространственной ограниченной круговой задачи трех тел , полученные М.Л. Лидовым в 1961
- 4. Начало совпадает с притягивающим центром S радиус – с параметром ε (0 ≤ ε ≤1) ;
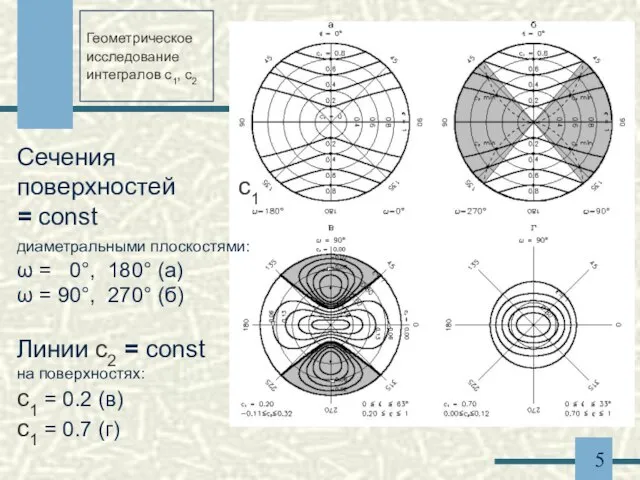
- 5. Геометрическое исследование интегралов c1, c2 Сечения поверхностей c1 = const диаметральными плоскостями: ω = 0°, 180°
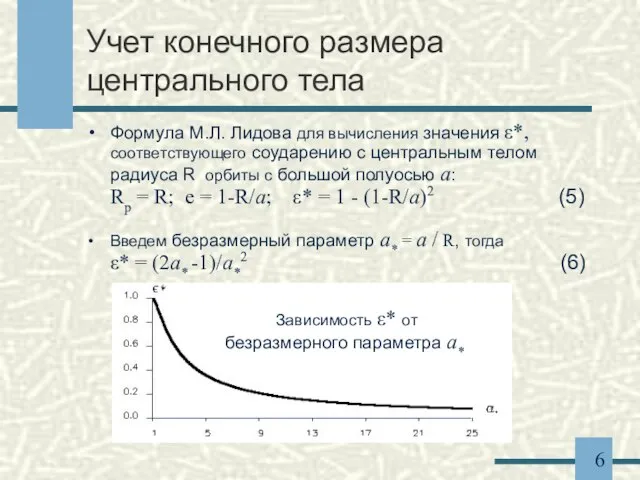
- 6. Учет конечного размера центрального тела Формула М.Л. Лидова для вычисления значения ε*, соответствующего соударению с центральным
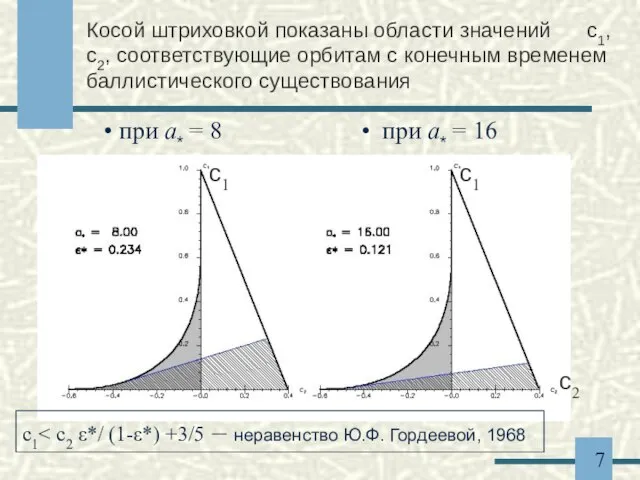
- 7. Косой штриховкой показаны области значений c1, c2, соответствующие орбитам с конечным временем баллистического существования при a*
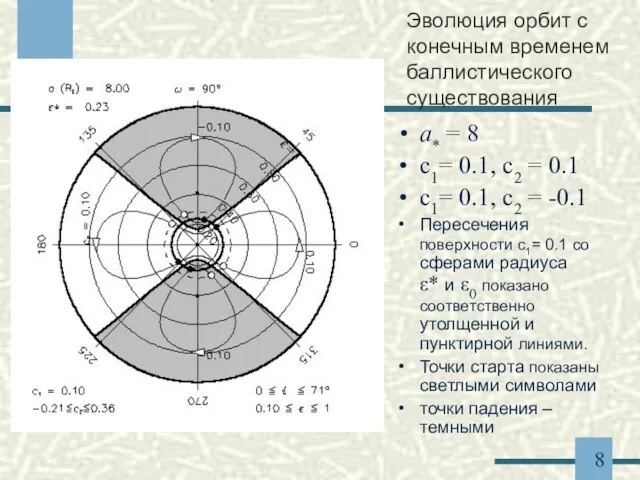
- 8. a* = 8 c1= 0.1, c2 = 0.1 c1= 0.1, c2 = -0.1 Пересечения поверхности c1=
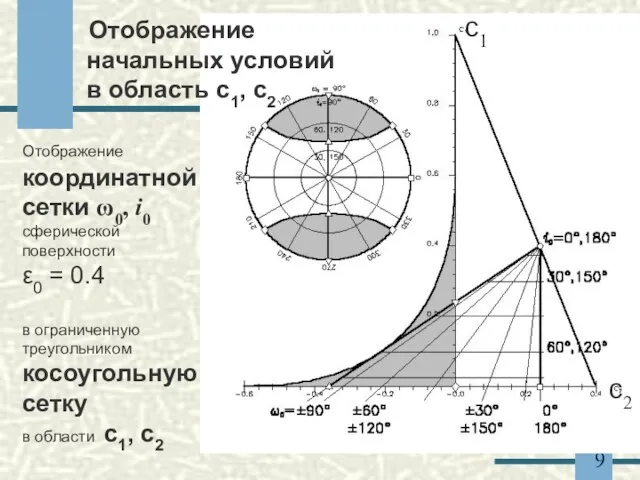
- 9. Отображение координатной сетки ω0, i0 сферической поверхности ε0 = 0.4 в ограниченную треугольником косоугольную сетку в
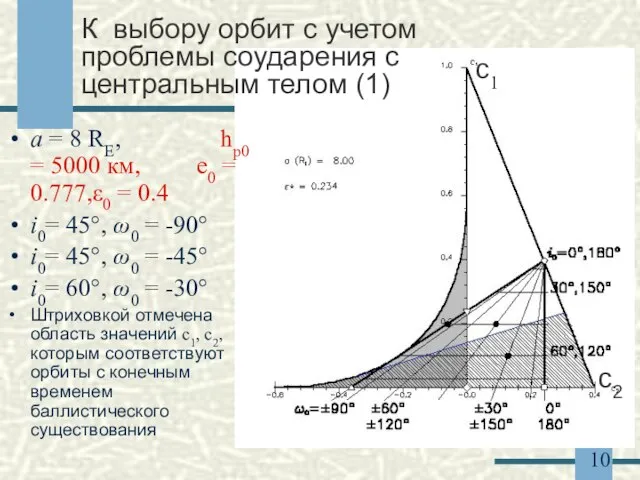
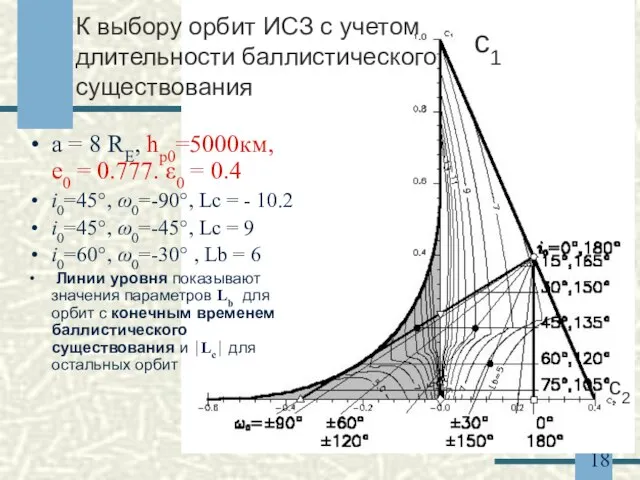
- 10. К выбору орбит с учетом проблемы соударения с центральным телом (1) a = 8 RE, hp0
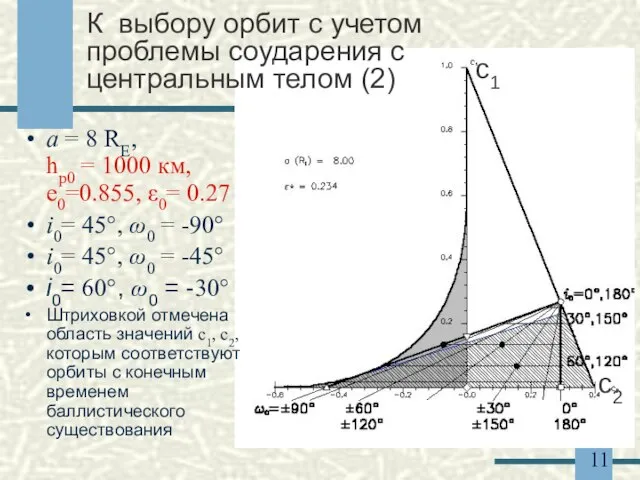
- 11. К выбору орбит с учетом проблемы соударения с центральным телом (2) a = 8 RE, hp0
- 12. Период эволюции и время баллистического существования Для вычисления времени баллистического существования орбит, эволюция которых заканчивается соударением
- 13. Период эволюции и время баллистического существования Для вычисления периода используются пределы интегрирования εmin , εmax, а
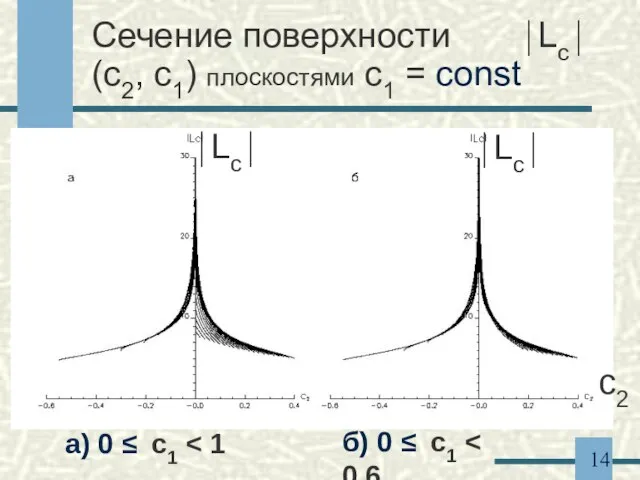
- 14. Сечение поверхности ⏐Lc⏐(c2, c1) плоскостями c1 = const a) 0 ≤ c1 б) 0 ≤ c1
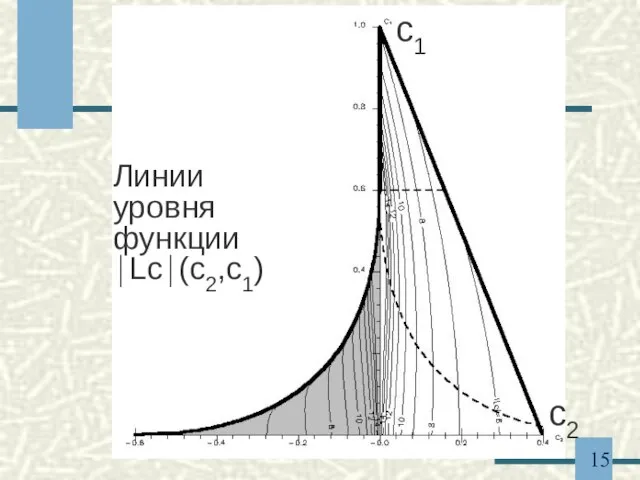
- 15. c1 c2 Линии уровня функции ⏐Lc⏐(c2,c1)
- 16. Время баллистического существования Обозначим Lr (c1, c2, a, ε0 , ω0) неполный эллиптический интеграл первого рода,
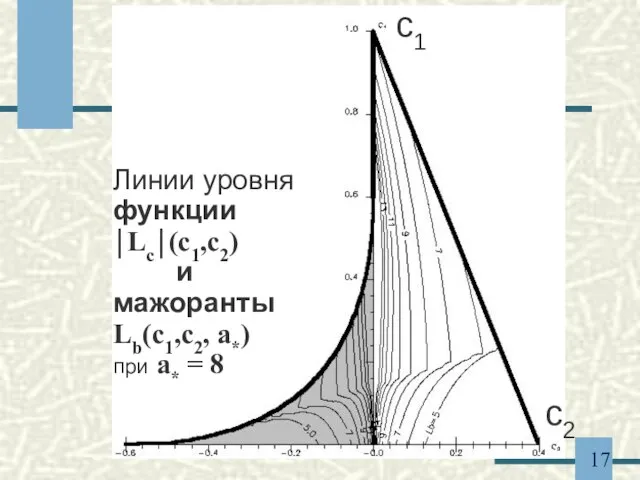
- 17. Линии уровня функции ⏐Lc⏐(c1,c2) и мажоранты Lb(c1,c2, a*) при a* = 8 c1 c2
- 18. a = 8 RE, hp0=5000км, e0 = 0.777. ε0 = 0.4 i0=45°, ω0=-90°, Lc = -
- 19. Анализ периода эволюции элементов орбиты и времени баллистического существования Преобразуем выражение (9) для периода T, чтобы
- 20. Анализ периода эволюции элементов орбиты и времени баллистического существования Запишем выражение безразмерного периода T* через ⏐Lc⏐и
- 21. Анализ периода эволюции элементов орбиты и времени баллистического существования Введем следующие численные значения характерного размера l
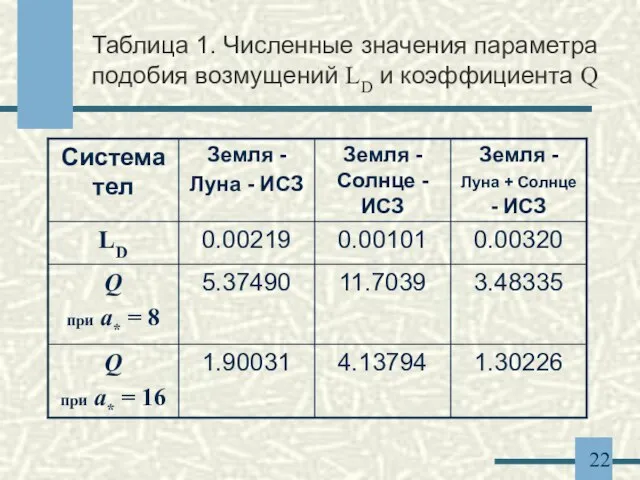
- 22. Таблица 1. Численные значения параметра подобия возмущений LD и коэффициента Q
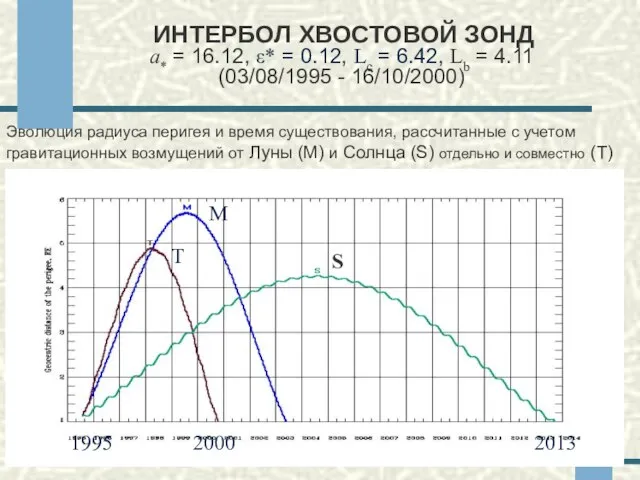
- 23. ИНТЕРБОЛ ХВОСТОВОЙ ЗОНД a* = 16.12, ε* = 0.12, Lc = 6.42, Lb = 4.11 (03/08/1995
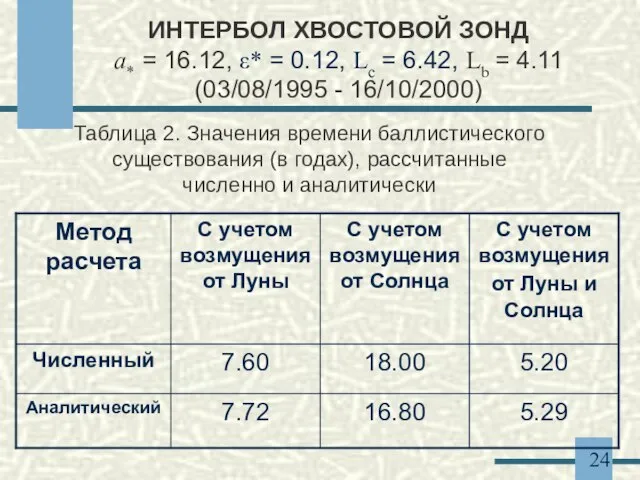
- 24. ИНТЕРБОЛ ХВОСТОВОЙ ЗОНД a* = 16.12, ε* = 0.12, Lc = 6.42, Lb = 4.11 (03/08/1995
- 26. Скачать презентацию









 Умножение суммы на число
Умножение суммы на число Презентация по обществознанию на тему _Правовое государство_ (9 класс)
Презентация по обществознанию на тему _Правовое государство_ (9 класс) Классификация организаций в сфере инфокоммуникаций
Классификация организаций в сфере инфокоммуникаций Педагогическая психология
Педагогическая психология  Бронхит. Лихорадка Fever
Бронхит. Лихорадка Fever Политическая система общества
Политическая система общества Адаптация человека и функциональное состояние
Адаптация человека и функциональное состояние Обзор решения 1С:Управление автотранспортом
Обзор решения 1С:Управление автотранспортом Етапи розвитку теорії ризикології
Етапи розвитку теорії ризикології Наказание. Доводы за и против
Наказание. Доводы за и против Дистанционные олимпиады
Дистанционные олимпиады pptx
pptx 6号地块35/0.4kV供电方案汇报
6号地块35/0.4kV供电方案汇报 Стратегическое управление
Стратегическое управление Презентация на тему Физиология физических качеств
Презентация на тему Физиология физических качеств Упражнения к лекции 3, 4
Упражнения к лекции 3, 4 М Е Д И Т А Ц И Я
М Е Д И Т А Ц И Я Сан-Марино
Сан-Марино Здоровый образ жизни и его составляющие
Здоровый образ жизни и его составляющие Wet Air - увлажнитель воздуха для людей болеющих астмой. Проект
Wet Air - увлажнитель воздуха для людей болеющих астмой. Проект Появление трамвая
Появление трамвая Организация исследовательской и проектно-творческой деятельности учащихся
Организация исследовательской и проектно-творческой деятельности учащихся РЕКОМЕНДАЦИИ ПО ОКАЗАНИЮ ПСИХОЛОГИЧЕСКОЙ ПОМОЩИ СЕМЬЕ И ДЕТЯМ
РЕКОМЕНДАЦИИ ПО ОКАЗАНИЮ ПСИХОЛОГИЧЕСКОЙ ПОМОЩИ СЕМЬЕ И ДЕТЯМ Презентация на тему ПРОФЕССИЯ Ветеринарный врач
Презентация на тему ПРОФЕССИЯ Ветеринарный врач  Презентация на тему Рынок труда и заработная плата
Презентация на тему Рынок труда и заработная плата  Нахождение части от целого и целого по значению его части
Нахождение части от целого и целого по значению его части Презентация на тему Лиственные и хвойные растения
Презентация на тему Лиственные и хвойные растения  Иван Александрович Гончаров(1812 – 1891)
Иван Александрович Гончаров(1812 – 1891)