Содержание
- 2. Данная презентация предназначена для проведения обобщающего урока по курсу геометрии 7 класс. Продолжительность показа презентации зависит
- 3. Аксиомы Точки и прямые Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки
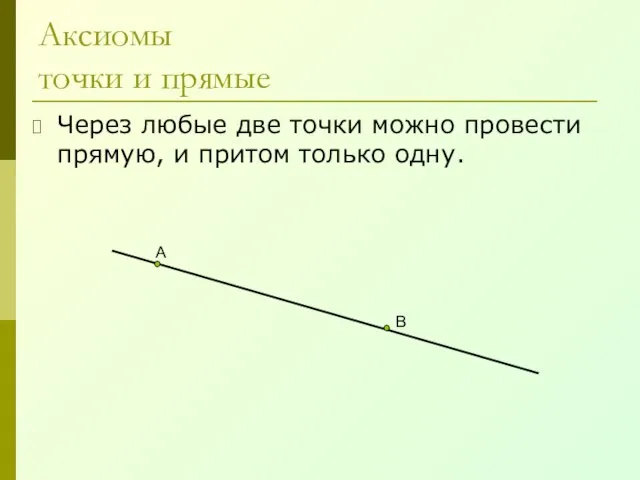
- 4. Аксиомы точки и прямые Через любые две точки можно провести прямую, и притом только одну. А
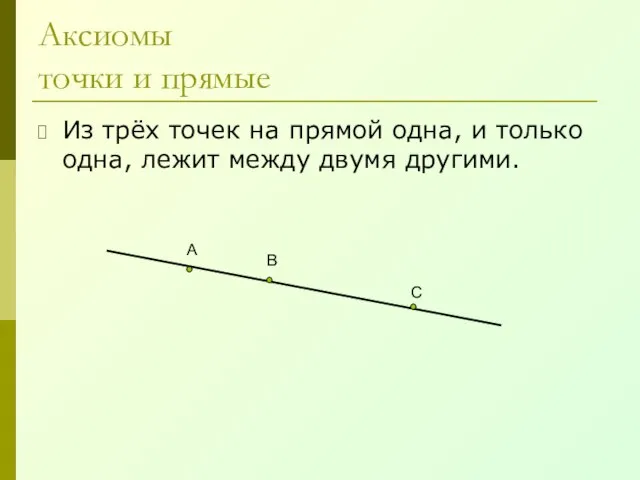
- 5. Аксиомы точки и прямые Из трёх точек на прямой одна, и только одна, лежит между двумя
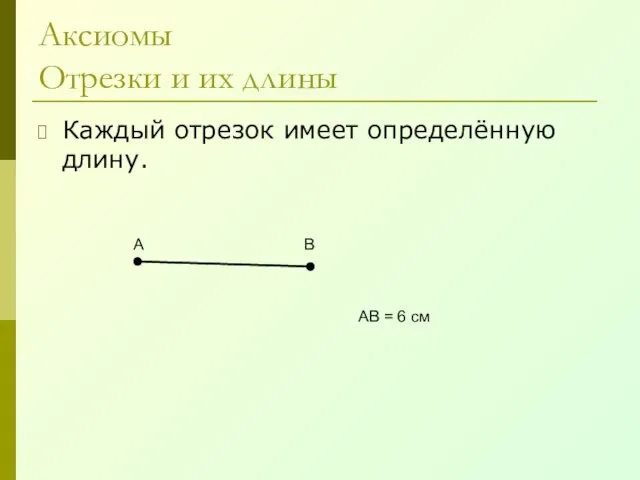
- 6. Аксиомы Отрезки и их длины Каждый отрезок имеет определённую длину. А В АВ = 6 см
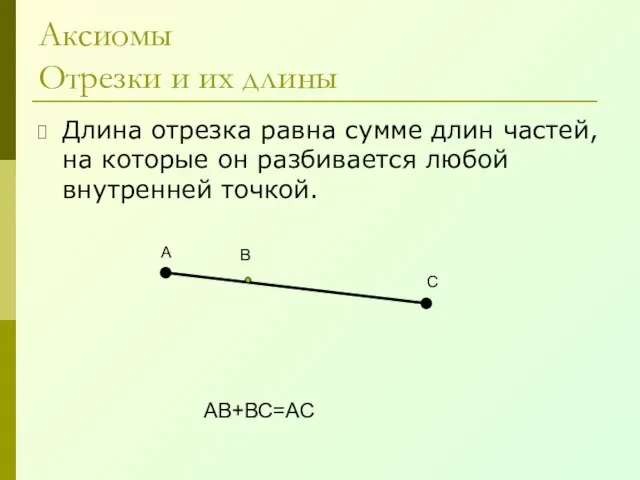
- 7. Аксиомы Отрезки и их длины Длина отрезка равна сумме длин частей, на которые он разбивается любой
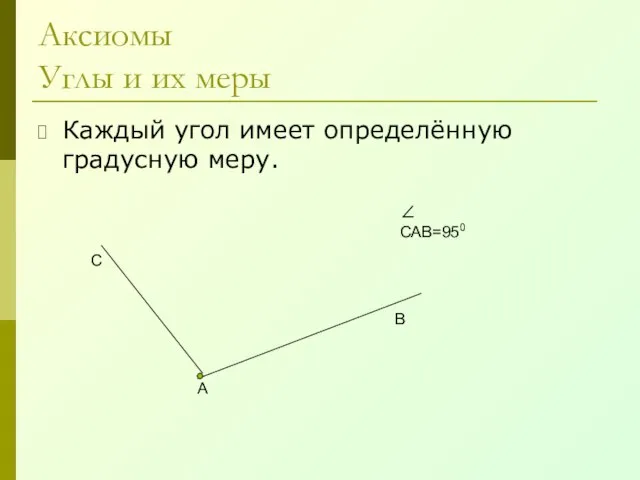
- 8. Аксиомы Углы и их меры Каждый угол имеет определённую градусную меру. А В С ∠ САВ=950
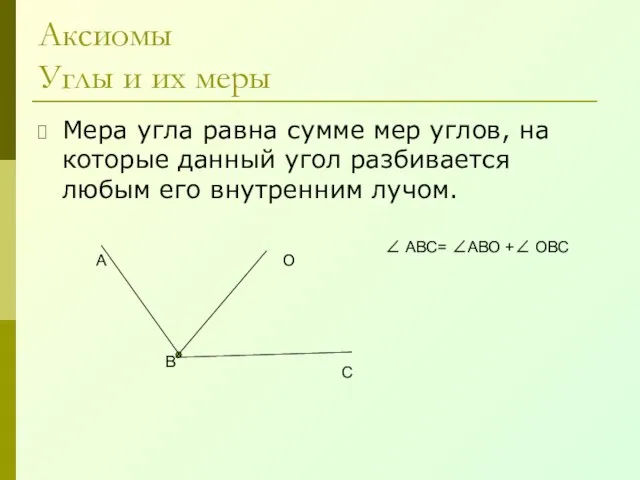
- 9. Аксиомы Углы и их меры Мера угла равна сумме мер углов, на которые данный угол разбивается
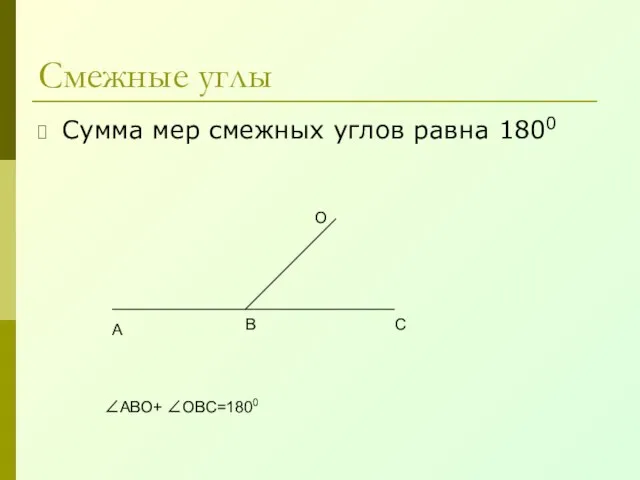
- 10. Смежные углы Сумма мер смежных углов равна 1800 А В С О ∠АВО+ ∠ОВС=1800
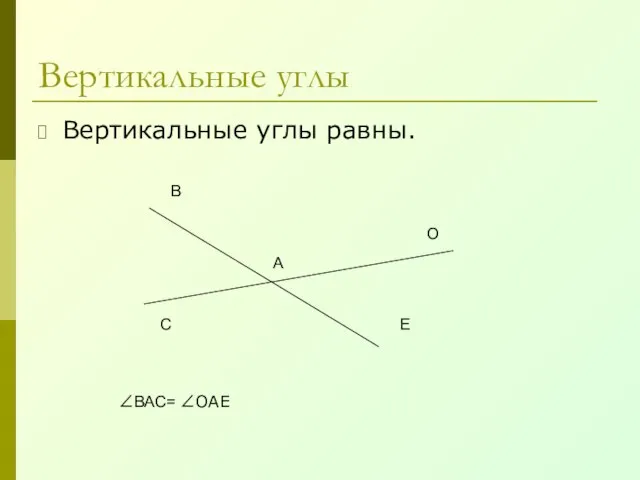
- 11. Вертикальные углы Вертикальные углы равны. А В С О Е ∠ВАС= ∠ОАЕ
- 12. Параллельные прямые определение Прямые называются параллельными, если -они лежат в одной плоскости -они не пересекаются а
- 13. Параллельные прямые Признаки Если две прямые с поперечиной образуют равные накрест лежащие углы, то прямые параллельны
- 14. Параллельные прямые Признаки Если сумма внутренних односторонних углов равна 1800 ,то прямые параллельны 1 2 3
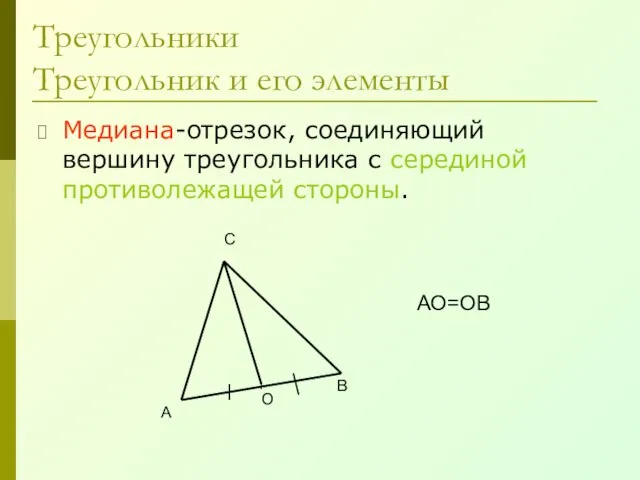
- 15. Треугольники Треугольник и его элементы Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. А В С
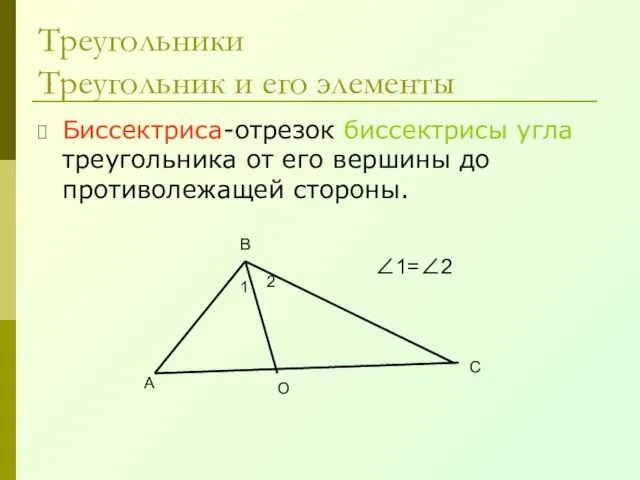
- 16. Биссектриса-отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны. Треугольники Треугольник и его элементы А
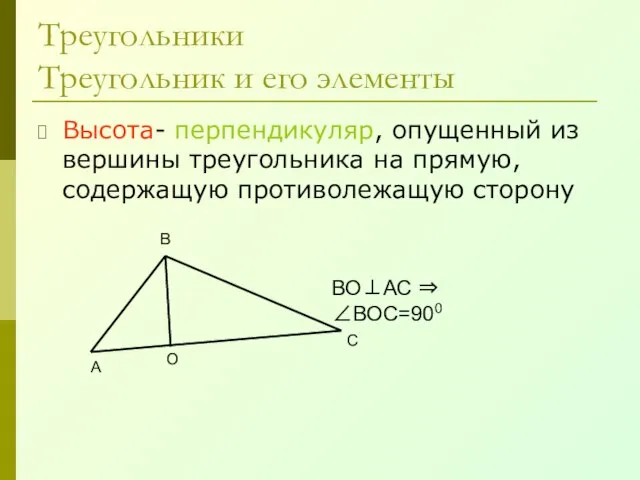
- 17. Треугольники Треугольник и его элементы Высота- перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону
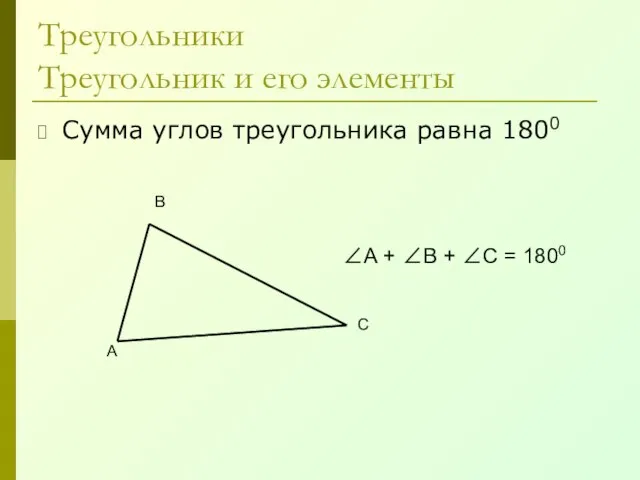
- 18. Треугольники Треугольник и его элементы Сумма углов треугольника равна 1800 А В С ∠А + ∠В
- 19. Треугольники Треугольник и его элементы Угол, смежный с углом треугольника, называют внешним углом. . А В
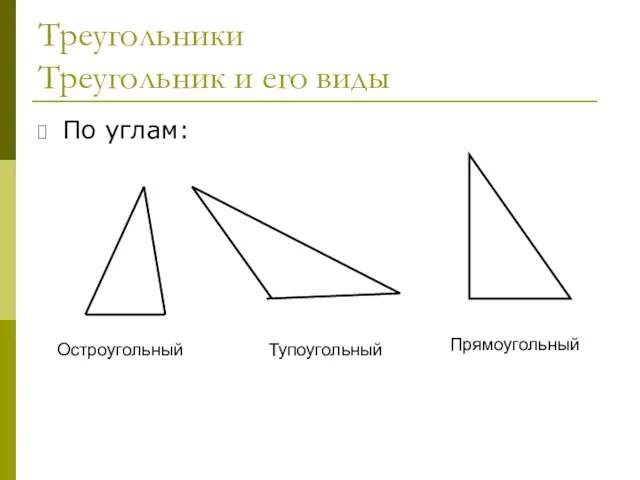
- 20. Треугольники Треугольник и его виды По углам: Остроугольный Тупоугольный Прямоугольный
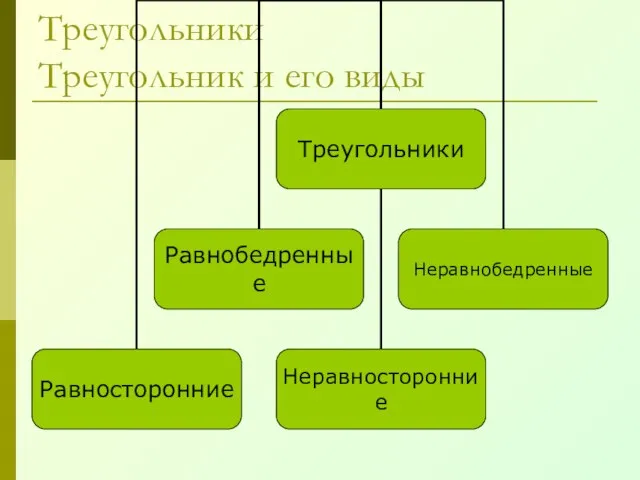
- 21. Треугольники Треугольник и его виды
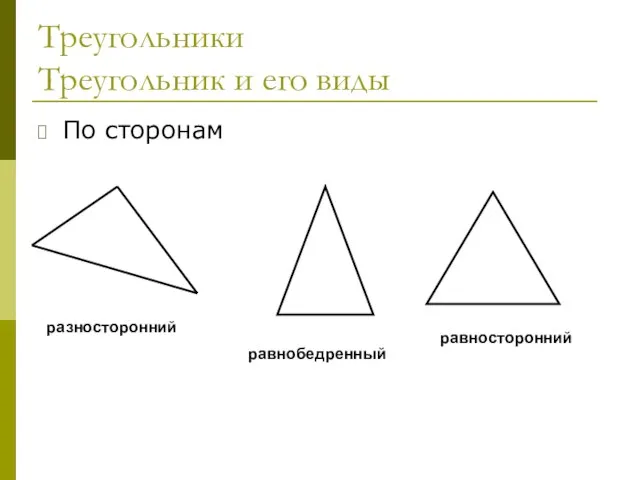
- 22. Треугольники Треугольник и его виды По сторонам разносторонний равнобедренный равносторонний
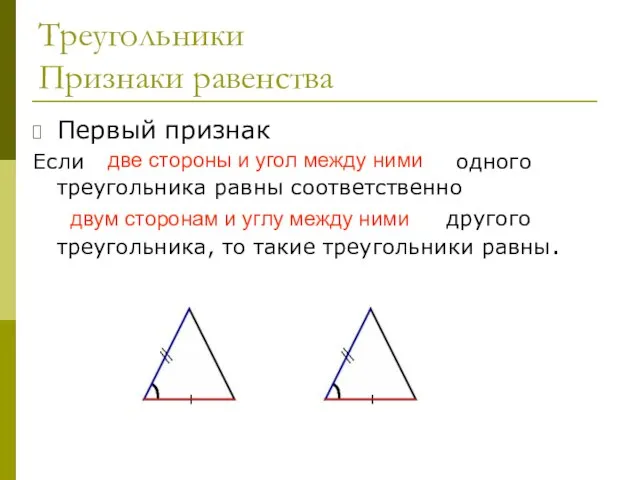
- 23. Треугольники Признаки равенства Первый признак Если две стороны и угол между ними одного треугольника равны соответственно
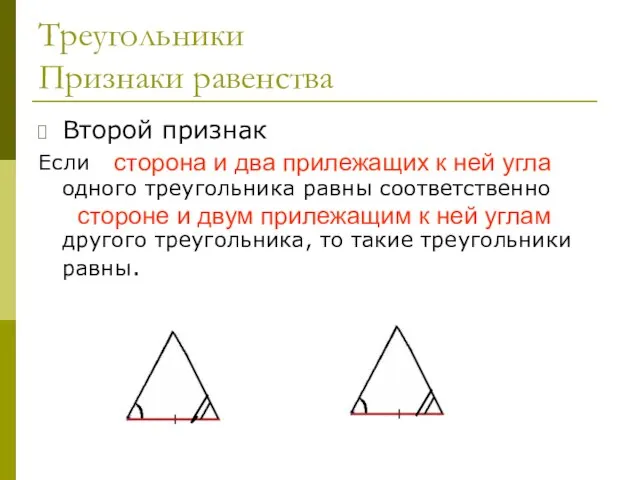
- 24. Треугольники Признаки равенства Второй признак Если сторона и два прилежащих к ней угла одного треугольника равны
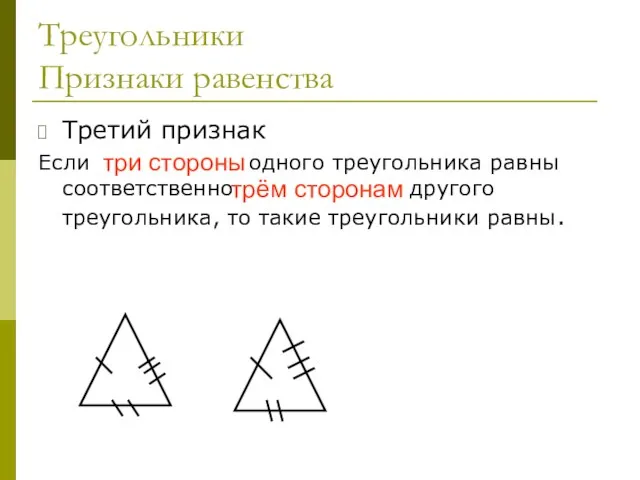
- 25. Треугольники Признаки равенства Третий признак Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника,
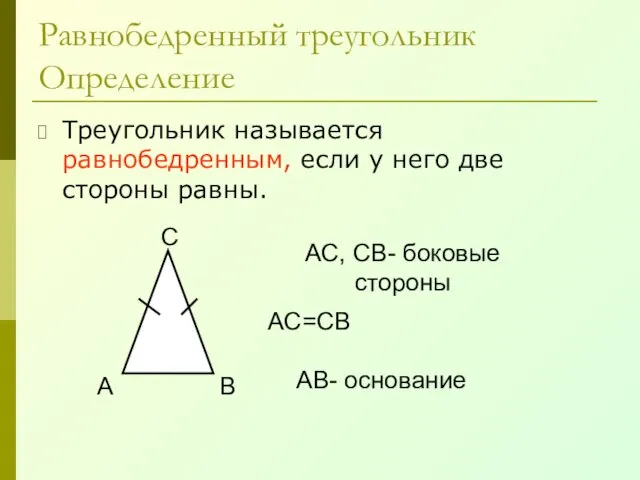
- 26. Равнобедренный треугольник Определение Треугольник называется равнобедренным, если у него две стороны равны. А В С АС,
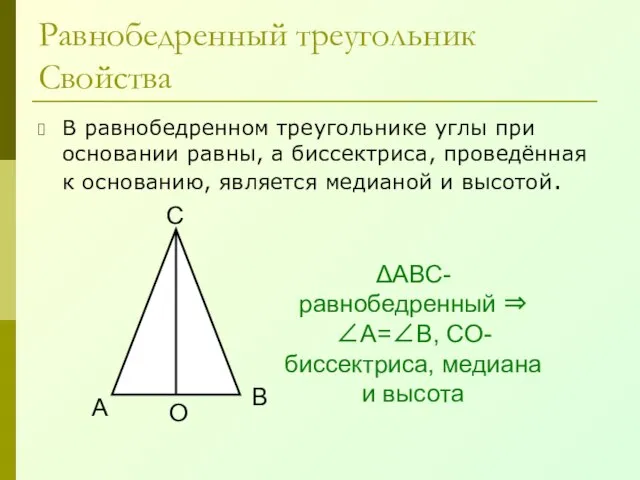
- 27. Равнобедренный треугольник Свойства В равнобедренном треугольнике углы при основании равны, а биссектриса, проведённая к основанию, является
- 28. Равнобедренный треугольник Признаки Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана
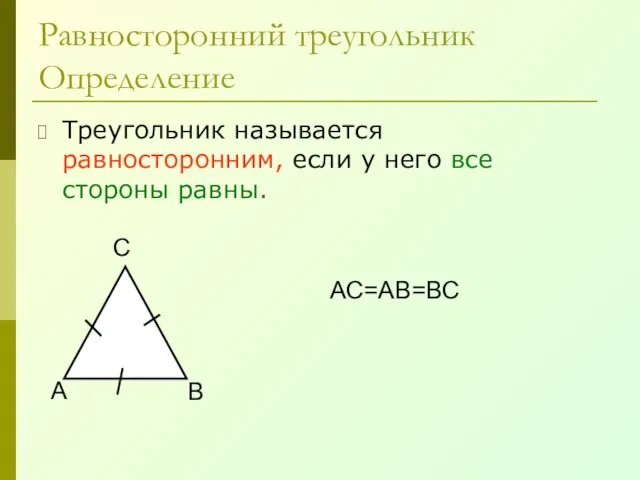
- 29. Равносторонний треугольник Определение Треугольник называется равносторонним, если у него все стороны равны. А В С АС=АВ=ВС
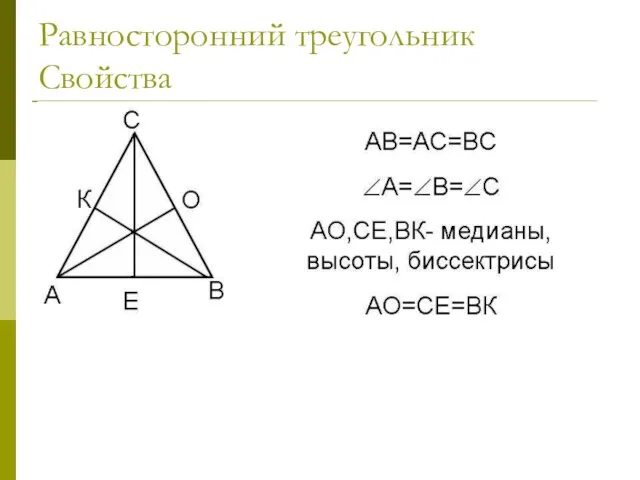
- 30. Равносторонний треугольник Свойства В равностороннем треугольнике все углы равны. В равностороннем треугольнике каждая биссектриса является медианой
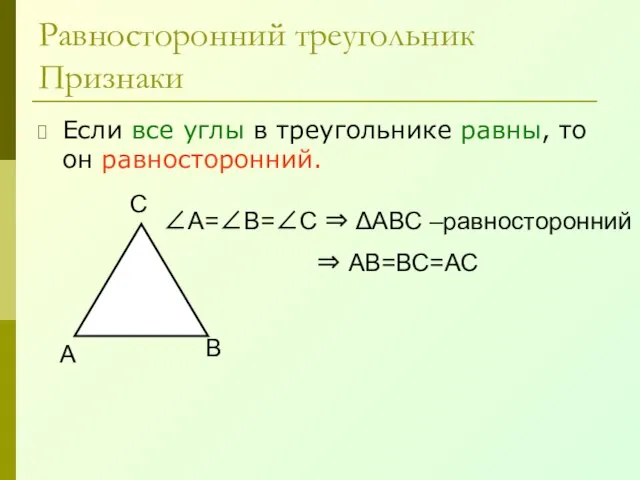
- 31. Равносторонний треугольник Признаки Если все углы в треугольнике равны, то он равносторонний. А В С ∠А=∠В=∠С
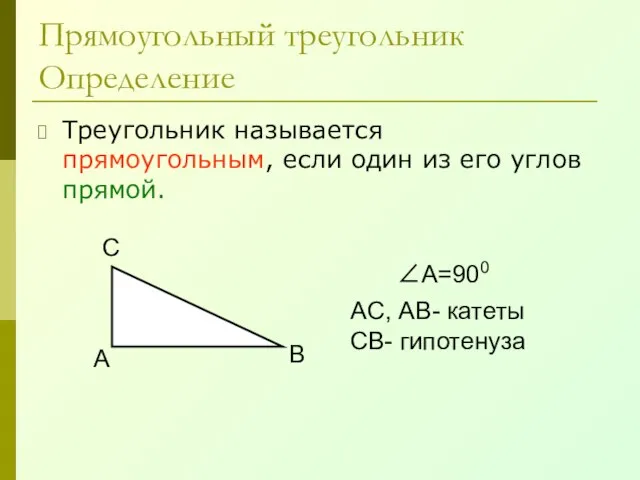
- 32. Прямоугольный треугольник Определение Треугольник называется прямоугольным, если один из его углов прямой. А В С ∠А=900
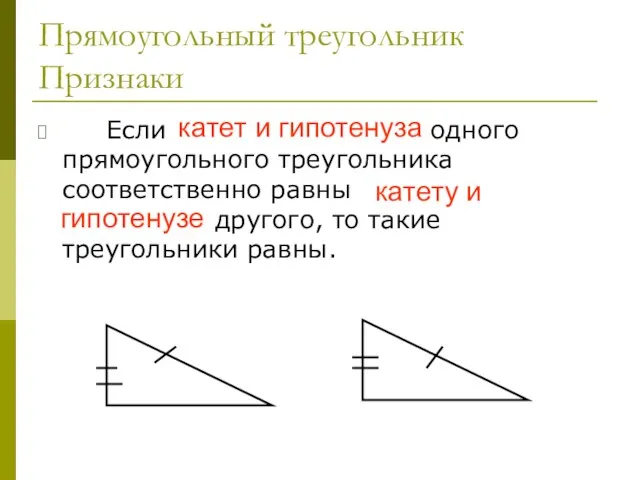
- 33. Прямоугольный треугольник Признаки Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого,
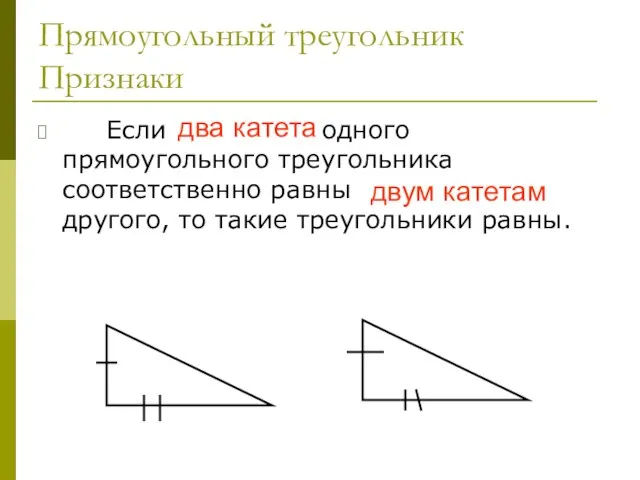
- 34. Прямоугольный треугольник Признаки Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то такие
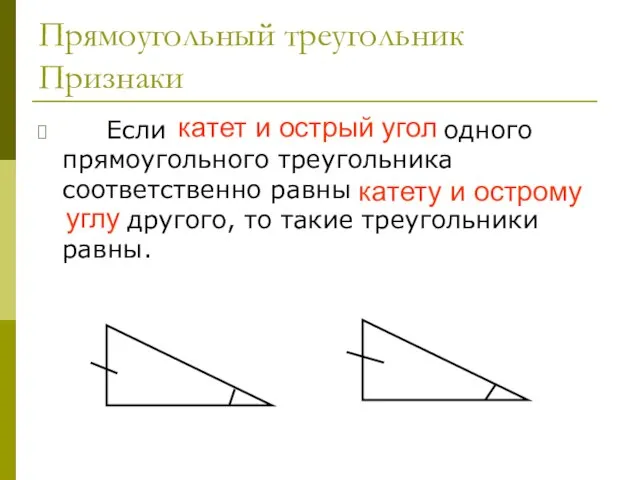
- 35. Прямоугольный треугольник Признаки Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому
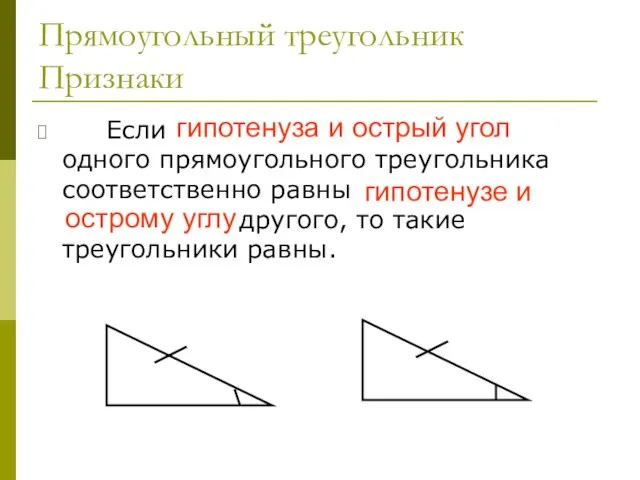
- 36. Прямоугольный треугольник Признаки Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому
- 37. Прямоугольный треугольник Свойства Катет прямоугольного треугольника, лежащий против угла 300, равен половине гипотенузы. А С В
- 39. Скачать презентацию








 Изображения изделий и их обозначения при выполнении графических конструкторских документов
Изображения изделий и их обозначения при выполнении графических конструкторских документов Использование функций
Использование функций Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Каникулы в международном детском лагере
Каникулы в международном детском лагере Язык есть исповедь народа
Язык есть исповедь народа Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных
Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных Физико-географическое районирование Северной Евразии
Физико-географическое районирование Северной Евразии  Узоры “тетёрки ” на печенье
Узоры “тетёрки ” на печенье Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты Весенний фестиваль для учащихся
Весенний фестиваль для учащихся 23 февраля. Поздравляем!
23 февраля. Поздравляем! Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн
Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн Звук и свет в лирике И. Анненского
Звук и свет в лирике И. Анненского Книжка-раскраска
Книжка-раскраска Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат
Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат Зачем живые организмы запасают питательные вещества?
Зачем живые организмы запасают питательные вещества? Особенности приема 2020 (колледж). Дистанционная подача документов
Особенности приема 2020 (колледж). Дистанционная подача документов Ресурсный Центр «Кристина»
Ресурсный Центр «Кристина» Проверка правильности кирпичной кладки
Проверка правильности кирпичной кладки Смешанное обучение – blended learning
Смешанное обучение – blended learning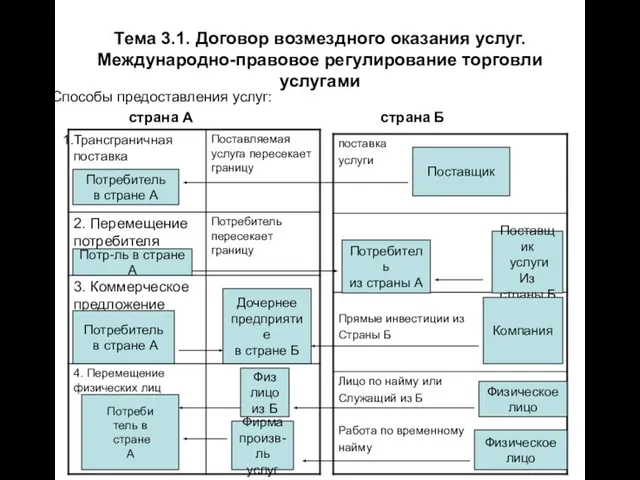 Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг
Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг Конвенция о правах ребенка
Конвенция о правах ребенка Богомолова Роза Александровна
Богомолова Роза Александровна Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания
Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания Принцип действия жидкокристаллических дисплеев
Принцип действия жидкокристаллических дисплеев Правила работы с обучающей презентацией
Правила работы с обучающей презентацией плакат
плакат ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития
ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития