Геометрия путешествий

Содержание
Титульный лист…………………… 1
Введение ……………………………. 3
Основная часть. Решение геометрических задач с помощью развёртки ………………………. 4-16
Задачи для самостоятельного решения … 17-19
Решения задач 1, 2 ……………….20-21
Вывод …………………………………… 22
Отзыв руководителя ……………… 23
Литература и ресурсы ……………..24

Учитель математики Иван Иванович приглашает Вас на урок- путешествие. Точнее путешествовать будете не Вы, Вы лишь поможете необычным путешественникам найти кратчайший путь, применив смекалку и математические знания.

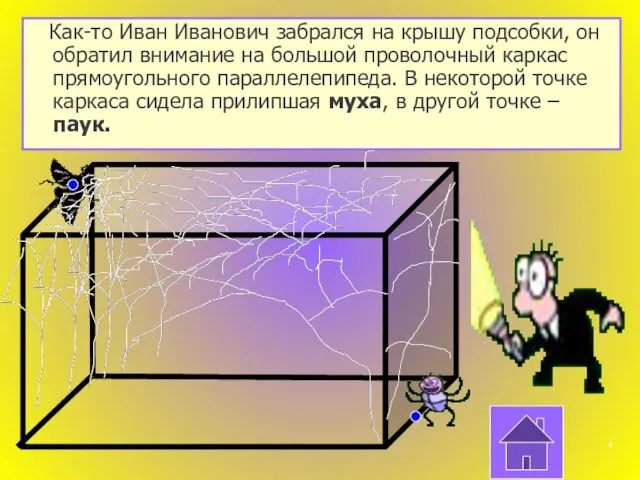
Как-то Иван Иванович забрался на крышу подсобки, он обратил внимание на большой проволочный каркас прямоугольного параллелепипеда. В некоторой точке каркаса сидела прилипшая муха, в другой точке – паук.

Иван Иванович внимательно наблюдал, как паук приближается к мухе, и думал: «А возможен ли более короткий путь?»

Надо предложить эту задачку ученикам?

«Продвинутые» ученики быстро сообразили, что можно поискать ответ в Интернете, и отыскали похожую задачу Г. Дьюдени - английского изобретателя головоломок - задачу о пауке и мухе. Впервые она была опубликована в 1903 году в одной английской газете.

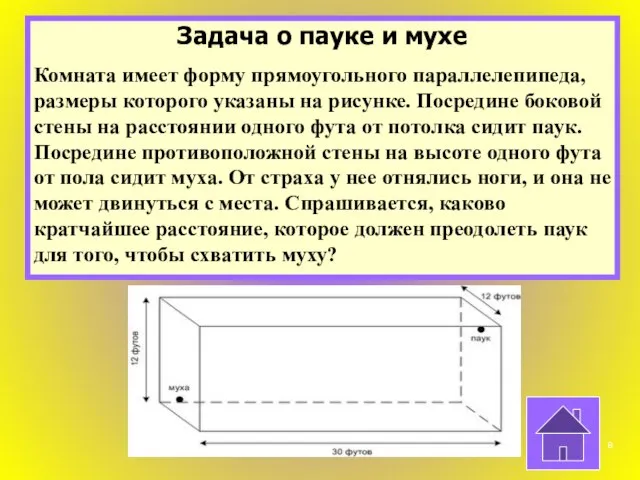
Задача о пауке и мухе
Комната имеет форму прямоугольного параллелепипеда, размеры которого указаны на рисунке. Посредине боковой стены на расстоянии одного фута от потолка сидит паук. Посредине противоположной стены на высоте одного фута от пола сидит муха. От страха у нее отнялись ноги, и она не может двинуться с места. Спрашивается, каково кратчайшее расстояние, которое должен преодолеть паук для того, чтобы схватить муху?

Для решения этой задачи нужно построить развертку граней прямоугольного параллепипеда и провести на ней прямую от места нахождения паука к точке, где сидит муха. Поскольку построить развёртку можно многими способами, то нужно выбрать среди них ту, которая дает кратчайшее расстояние.

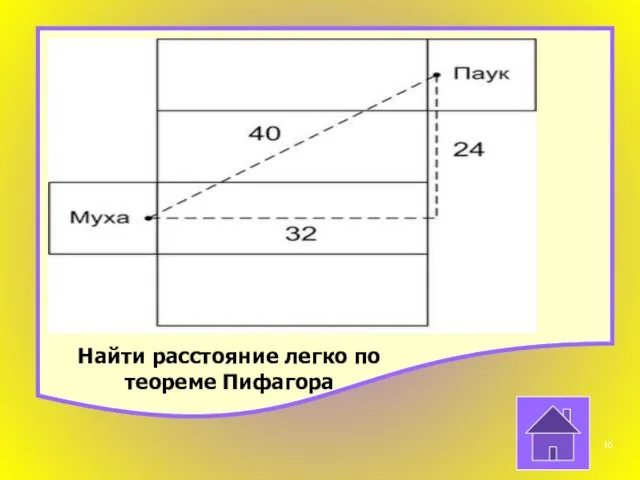
Найти расстояние легко по теореме Пифагора

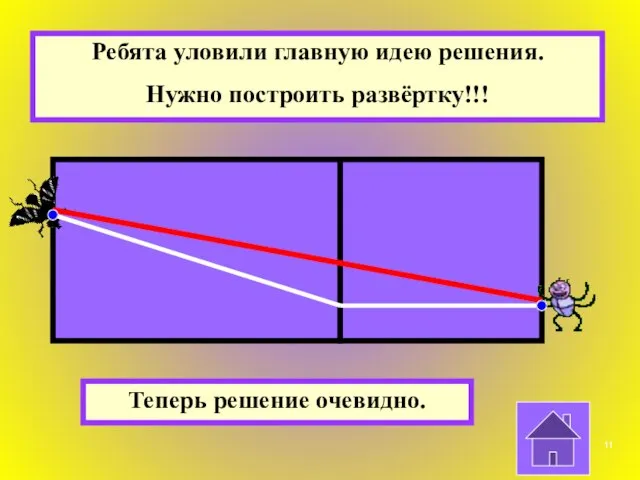
Ребята уловили главную идею решения.
Нужно построить развёртку!!!
Теперь решение очевидно.

Учитель доволен.
Молодцы, ребята!

В библиотеке, в книге Надя нашла ещё одну подобную интересную задачу и предложила решить её одноклассникам.
Путь мухи
На внутренней стенке стеклянной цилиндрической банки виднеется капля мёда в 3 см от верхнего края сосуда. На наружной стенке в точке диаметрально противоположной уселась муха. Укажите мухе кратчайший путь до медовой капли. Высота банки 20 см; диаметр 10 см.

Они быстро её решили. Ведь они уже знали, что в решении подобных задач очень помогает развёртка объёмной фигуры.
А Вы, сможете её решить самостоятельно?

Путь мухи
На внутренней стенке стеклянной цилиндрической банки виднеется капля мёда в 3 см от верхнего края сосуда. На наружной стенке в точке диаметрально противоположной уселась муха. Укажите мухе кратчайший путь до медовой капли. Высота банки 20 см; диаметр 10 см.
Подсказка

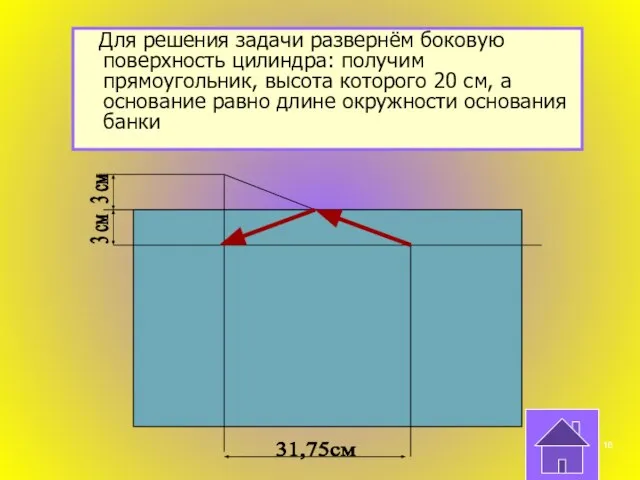
Для решения задачи развернём боковую поверхность цилиндра: получим прямоугольник, высота которого 20 см, а основание равно длине окружности основания банки
3 см
31,75см
3 см

В интернете мы нашли аналогичные задачи. Попробуйте их решить, вооружившись приобретёнными знаниями.

Задача 1. Паук в банке.
В стеклянной банке высотой 4 дюйма, с длиной окружности 6 дюймов сидит мой паук. Сейчас он расположился в 1 дюйме от нижнего края банки. А напротив него, всего в 1 дюйме от верхнего края, на внутренней стороне сидит муха. А теперь вопрос: какой путь к добыче будет для паука кратчайшим и сколько дюймов ему надо проползти?

Задача 2. Путь жука.
У дороги лежит тесаный гранитный камень в 30 см длины, 20 см высоты и такой же толщины (рис. 306). В точке А — жук, намеревающийся кратчайшим путем направиться к углу В.
Как пролегает этот кратчайший путь и какой он длины?

Решение задачи 1.
Чтобы решить эту задачу, необходимо «развернуть» банку (по сути, цилиндр) на плоскости. На рисунке у вас получится прямоугольник. Теперь точкой F обозначим нахождение мухи (по-английски fly), а паука – точкой S (spider). Левую сторону прямоугольника продолжим вверх еще на 1 дюйм (к точке B). Проведем линию BS, пересекающую верхнюю сторону прямоугольника в точке А. Именно в эту точку паук перебежит на верхний край банки. Траектория его движения окажется в развертке гипотенузой прямоугольного треугольника, больший катет которого равен 4 дюймам, а меньший – 3.Теперь легко посчитать, что гипотенуза, которая и есть кратчайший путь паука к добыче, равна 5 дюймам.

Решение задачи 2
Кратчайший путь легко определится, если мы мысленно повернем верхнюю грань камня так, чтобы она оказалась в одной плоскости с передней (рис. 317). Тогда станет очевидным, что кратчайший путь—прямая линия, соединяющая А и В. Какова длина этого пути? Мы имеем прямоугольный треугольник ABC, в котором АС = 40 см, СВ = 30 см. По Пифагору, третья сторона, АВ, должна равняться 50 см, потому что 302 + 402 = 502.
Итак, кратчайший путь АВ = 50 см.

Вывод
Многие, на первый взгляд трудные задачи, легко решаются с помощью развёртки соответствующей геометрической фигуры. Для их решения достаточно знаний и умений решения треугольников.

Отзыв руководителя
Данная презентация подготовлена учащимися как дополнительный материал по теме «Решение треугольников». Дополнительно учащиеся знакомятся с новым способом решения задач с помощью развёртки. В процессе работы учащиеся закрепили навыки работы с источниками, интернет ресурсами, самостоятельно изучили новый способ решения геометрических задач, проявили фантазию в представлении материала, научились работать в команде, рационально распределяя работу между членами группы. Удачно выбраны эффекты анимации геометрического представления задачи. В результате получилась интересная и полезная для уроков математики презентация.