Презентация на тему Теория вероятностей

Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

ИСТОРИЯ
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).
.

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики

ВЕРОЯТНОСТЬ
Вероя́тность (вероятностная мера) — численная мера степени объективной возможности наступления случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель — число всех равновозможных случаев.
ОБЛАДАЕТ СВОЙСТВОМ СИГМА-АДДИТИВНОСТИ (СЧЕТНОЙ АДДИТИВНОСТИ)

СЛУЧАЙНАЯ ВЕЛИЧИНА
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Формальное математическое определение следующее: пусть вероятностное пространство, тогда случайной величиной называется функция , измеримая относительно и борелевской σ-алгебры на . Вероятностное поведение случайной величины полностью описывается её распределением.

ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-то одной грани в данном случае в теории вероятностей называется элементарным событием , то есть:
- грань с одной точкой;
- грань с двумя точками;
- грань с шестью точками.

Множество всех граней и образует пространство элементарных событий подмножества которого называются случайными событиями .

В СЛУЧАЕ ОДНОКРАТНОГО ПОДБРАСЫВАНИЯ ИГРОВОЙ КОСТИ ПРИМЕРАМИ СОБЫТИЙ ЯВЛЯЮТСЯ
выпадение грани с нечётным количеством точек, то есть событие -это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие записывается как множество, содержащее элементарные события: , и
Таким образом,
выпадение грани с чётным количеством точек, то есть событие - это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие записывается как множество, содержащее элементарные события: , , и Таким образом, ;

Пространство элементарных событий Ω в случае бросания игральной кости

КЛАССИФИКАЦИЯ
Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения.
Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).
На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

Пример смешанной случайной величины - время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.
В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.
Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

МЕТОДЫ ОПИСАНИЯ
Для того, чтобы задать случайную величину необходимо с помощью функции распределения, плотности вероятности и характеристической функции определить вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.

Если случайная величина дискретная, то для полного и однозначного математического описания необходимо задать закон распределения вероятностей, то есть указать вероятности pk = P(ξ = xk) всех возможных значений случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения

Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» – с вероятностью q=1-p.
Закон распределения в этом случае определяется формулой Бернулли:

При стремлении n к бесконечности произведение np остаётся равной константе λ, а закон распределения сходится к закону Пуассона, который описывается следующей формулой:

Математи́ческое ожида́ние — мера среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через (например, от англ. Expected value или нем. Erwartungswert), в русской M[X] (возможно, от англ. Mean value, а возможно от русск. Математическое ожидание). В статистике часто используют обозначение μ

ОПРЕДЕЛЕНИЕ
Пусть задано вероятностное пространство
и определённая на нём случайная величина X. То есть, по определению, — измеримая функция. Тогда, если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или .. .

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Если FX(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

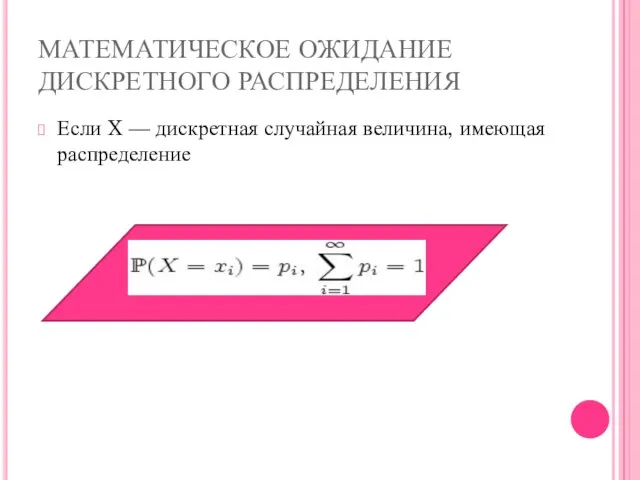
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОГО РАСПРЕДЕЛЕНИЯ
Если X — дискретная случайная величина, имеющая распределение

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ЦЕЛОЧИСЛЕННОЙ ВЕЛИЧИНЫ
Если X — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей