Содержание
- 2. Какие из следующих утверждений верны? Задание 15 (№ 169915) 1 2 3 4 Если угол равен
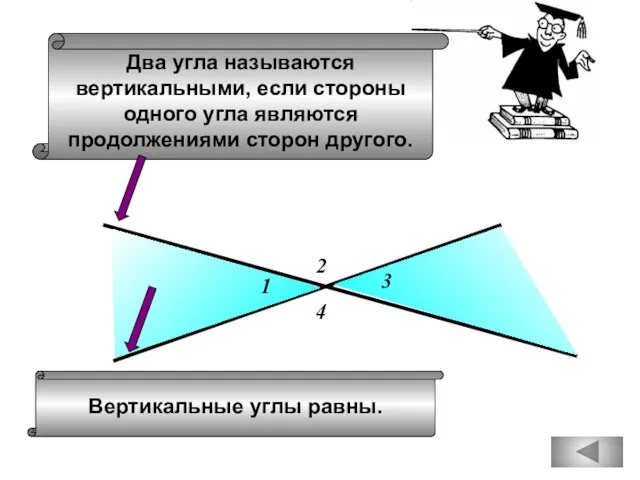
- 3. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. 2 4 1 3
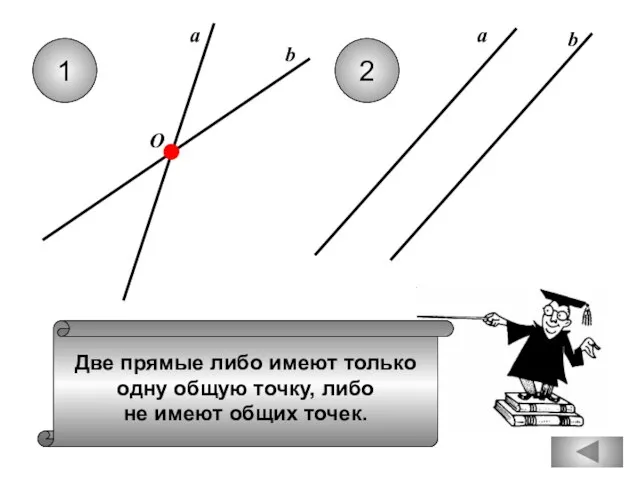
- 4. Две прямые либо имеют только одну общую точку, либо не имеют общих точек. 1 2 b
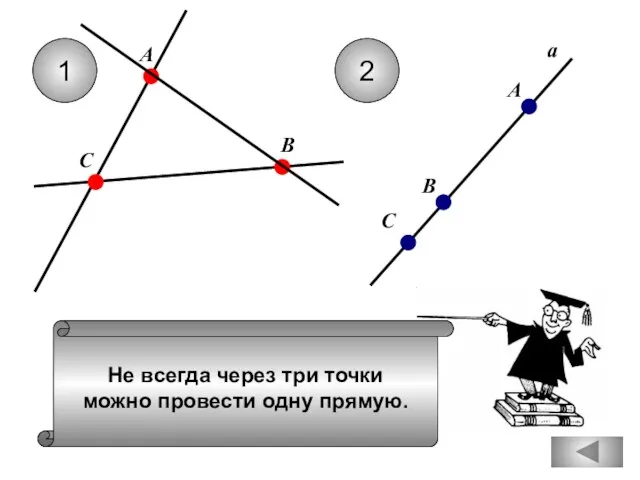
- 5. Не всегда через три точки можно провести одну прямую. 1 2 С А В а А
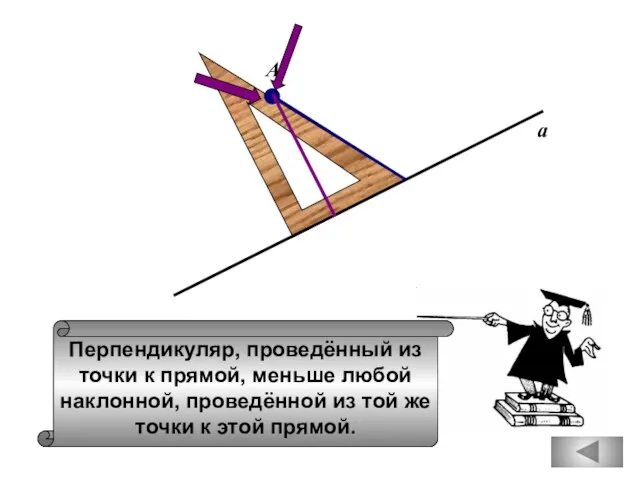
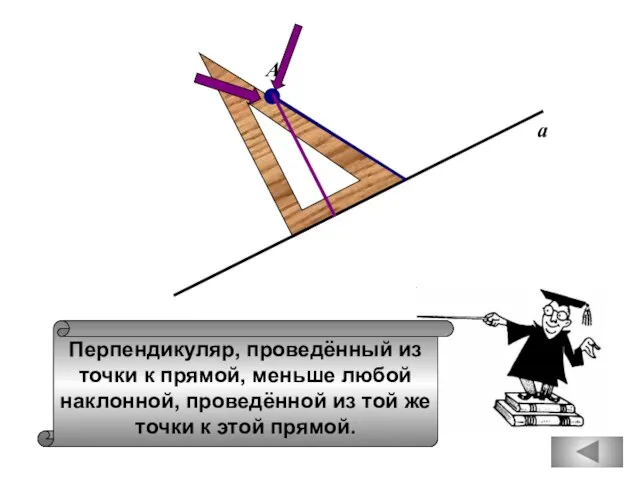
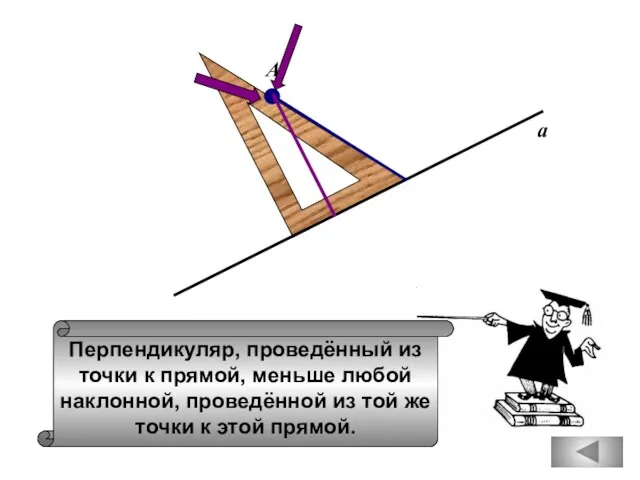
- 6. Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой
- 7. Какие из следующих утверждений верны? Задание 15 (№ 169916) 1 2 3 4 Если при пересечении
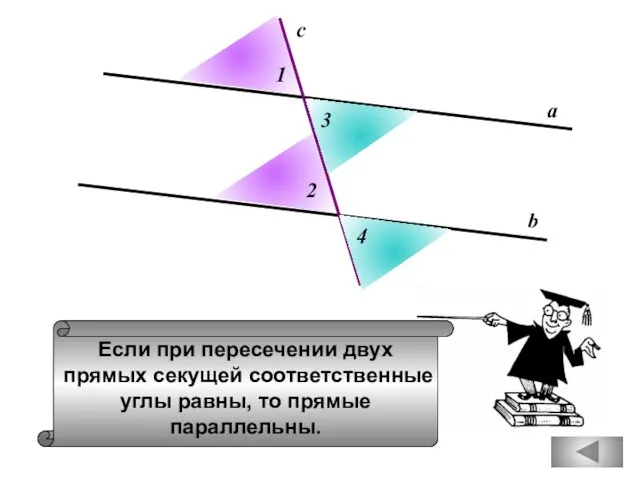
- 8. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. а b c 1
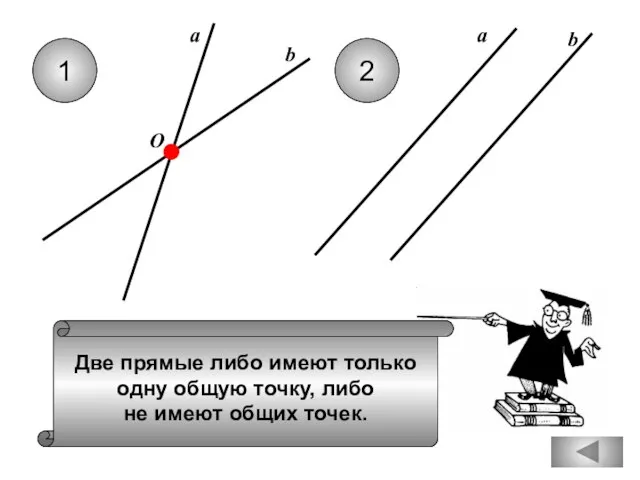
- 9. Две прямые либо имеют только одну общую точку, либо не имеют общих точек. 1 2 b
- 10. 1 b а 2 3
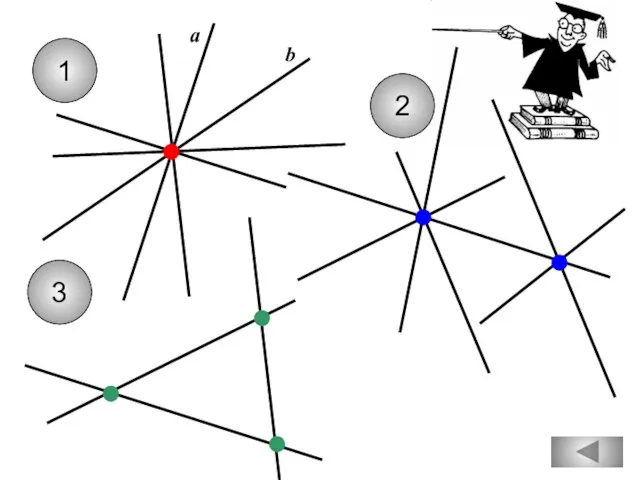
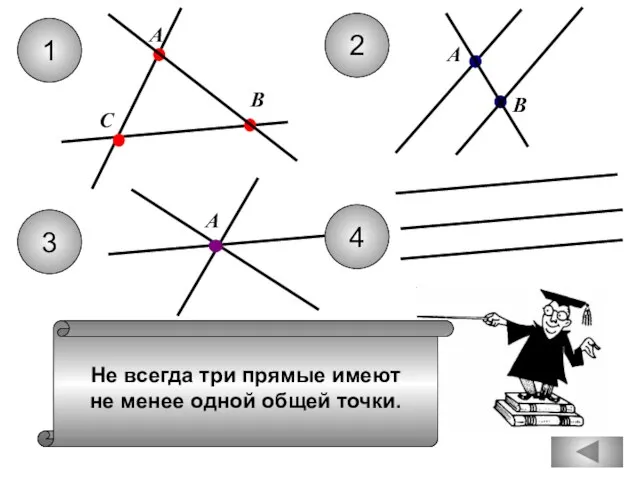
- 11. Не всегда три прямые имеют не менее одной общей точки. 1 2 С А В А
- 12. Какие из следующих утверждений верны? Задание 15 (№ 169917) 1 2 3 4 Если при пересечении
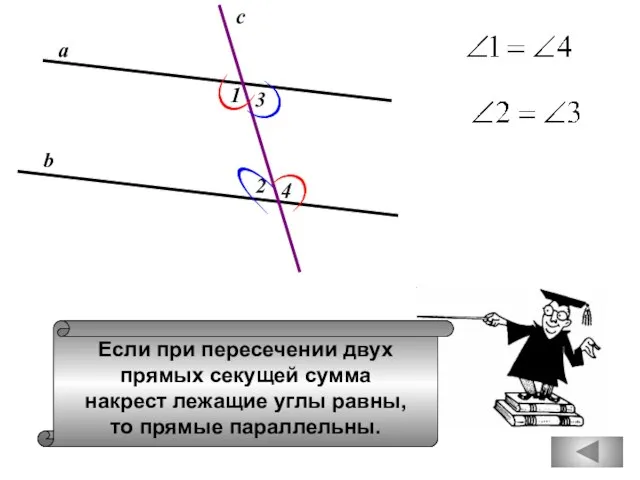
- 13. Если при пересечении двух прямых секущей сумма накрест лежащие углы равны, то прямые параллельны. а b
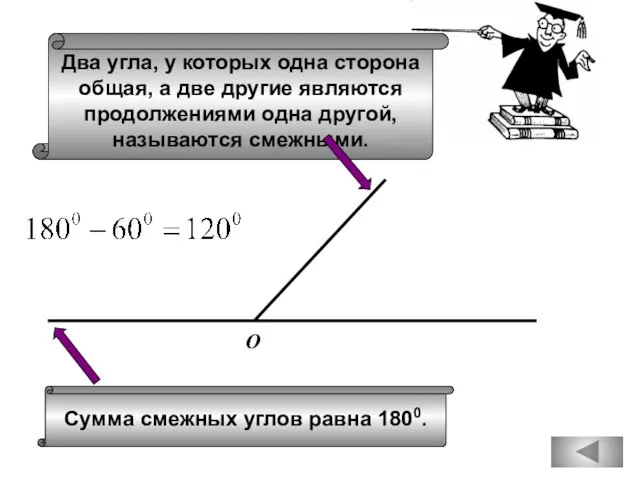
- 14. Сумма смежных углов равна 1800. Два угла, у которых одна сторона общая, а две другие являются
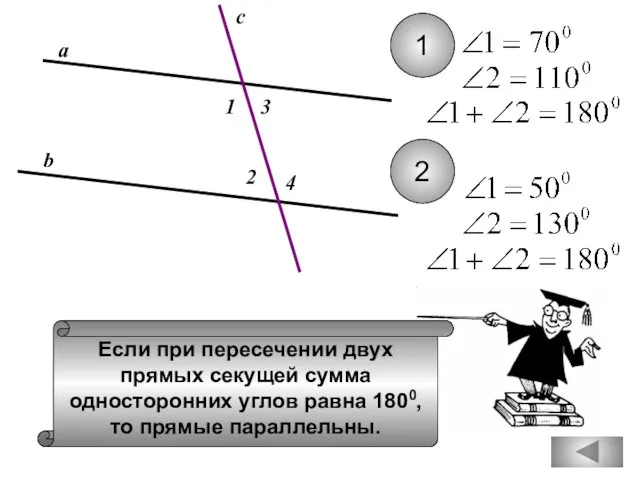
- 15. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны. а b
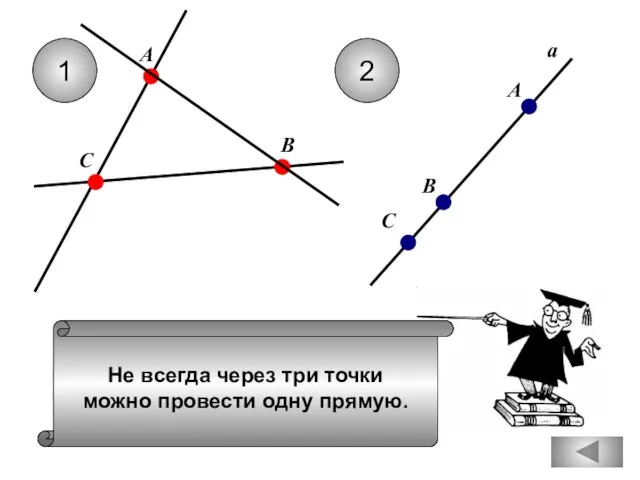
- 16. Не всегда через три точки можно провести одну прямую. 1 2 С А В а А
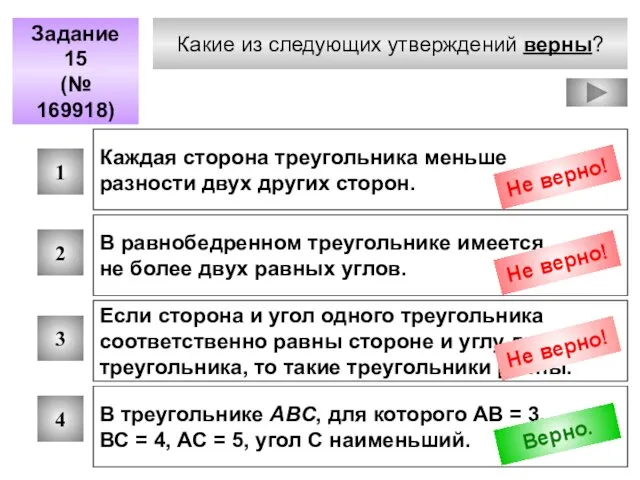
- 17. Какие из следующих утверждений верны? Задание 15 (№ 169918) 1 2 3 4 Каждая сторона треугольника
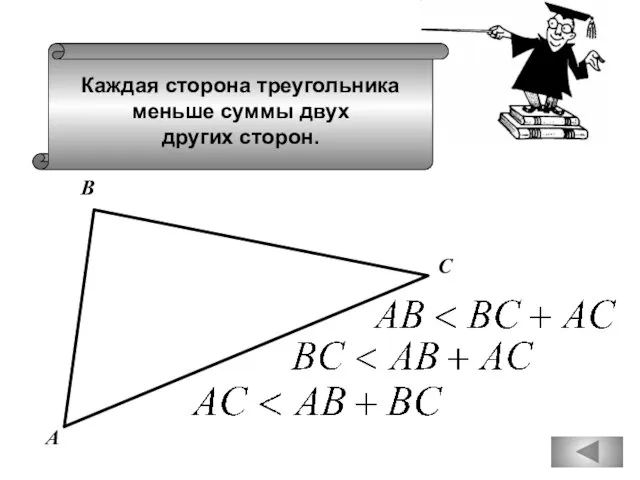
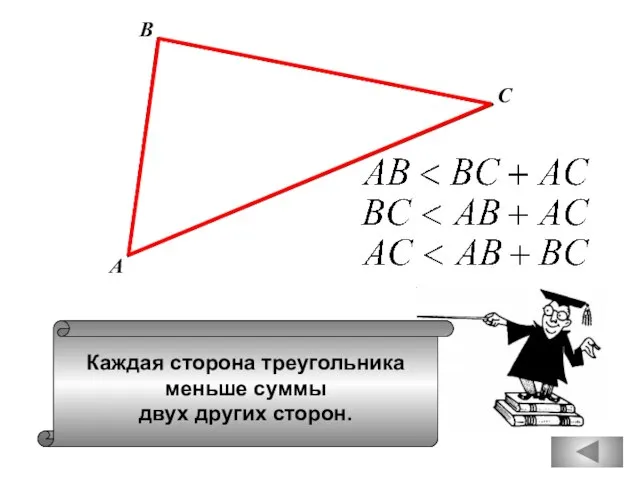
- 18. Каждая сторона треугольника меньше суммы двух других сторон. А В С
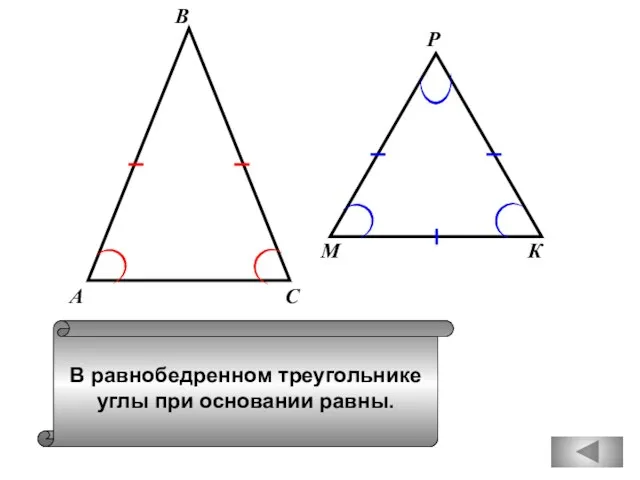
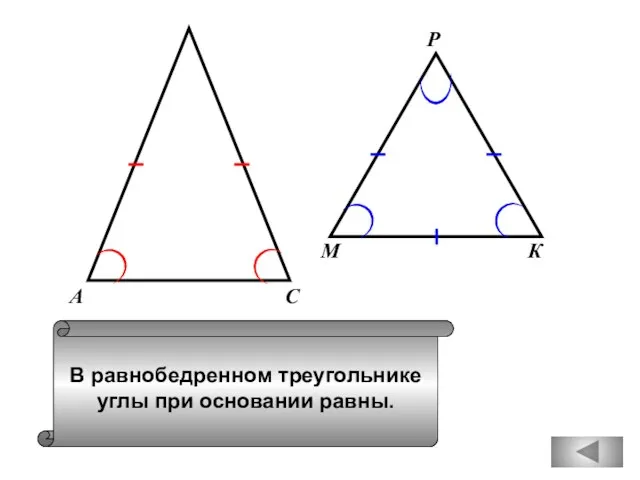
- 19. В равнобедренном треугольнике углы при основании равны. А В С М К Р
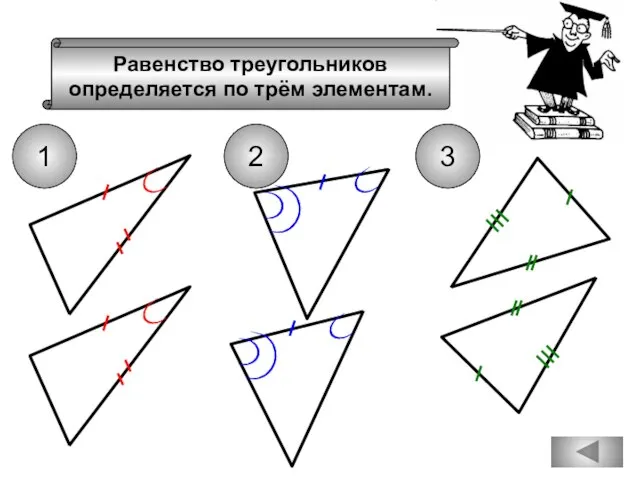
- 20. Вспомним признаки равенства треугольников 1 2 3 Равенство треугольников определяется по трём элементам.
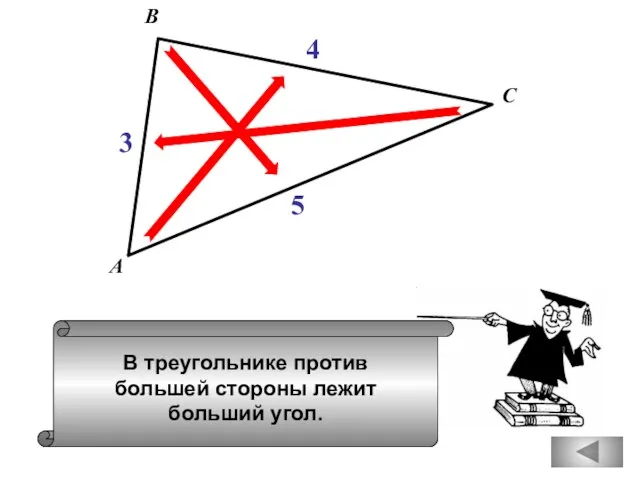
- 21. В треугольнике против большей стороны лежит больший угол. А В С 3 4 5
- 22. Какие из следующих утверждений верны? Задание 15 (№ 169919) 1 2 3 4 В треугольнике против
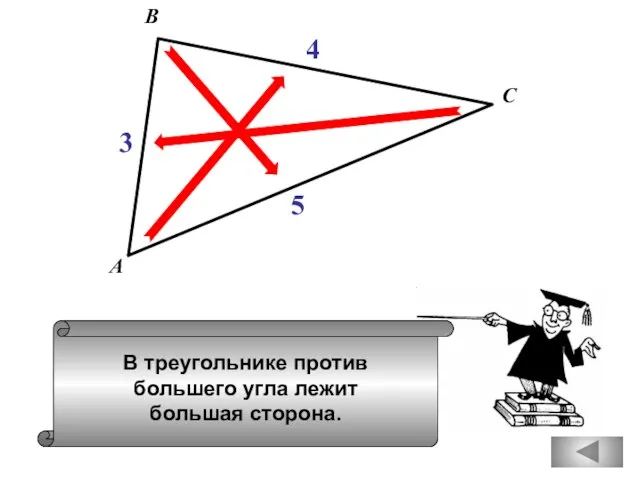
- 23. В треугольнике против большего угла лежит большая сторона. А В С 3 4 5
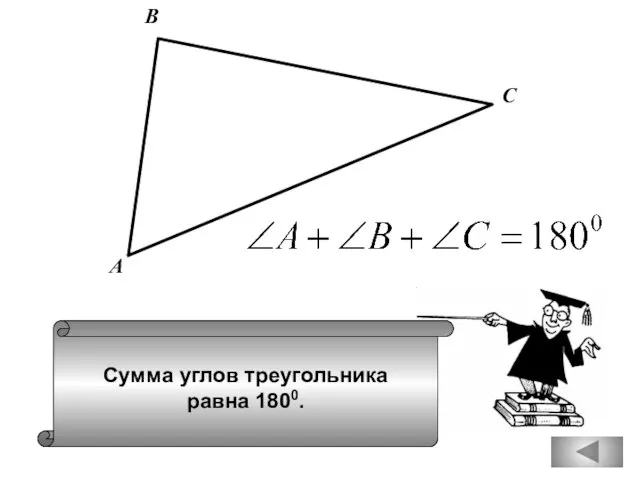
- 24. Сумма углов треугольника равна 1800. А В С
- 25. Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой
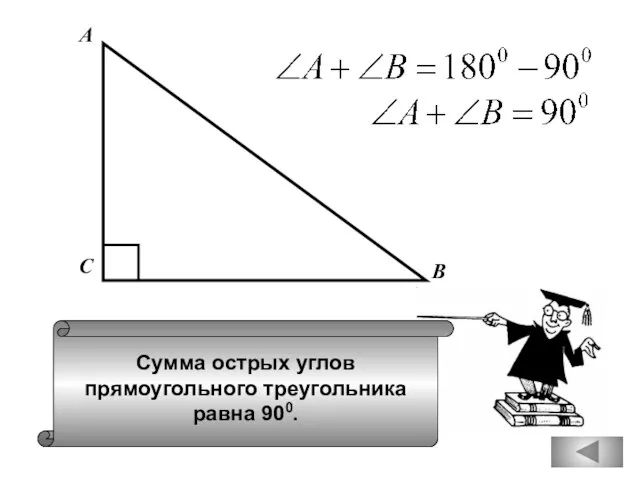
- 26. Сумма острых углов прямоугольного треугольника равна 900. А В С
- 27. Какие из следующих утверждений не верны? Задание 15 (№ 169920) 1 2 3 4 В треугольнике
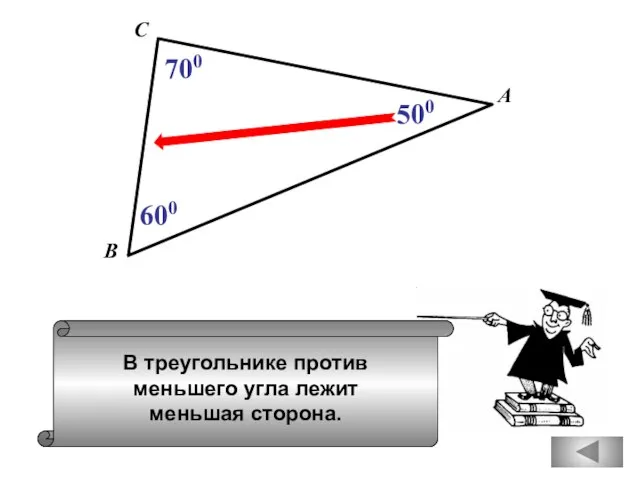
- 28. В треугольнике против меньшего угла лежит меньшая сторона. А В С 600 700 500
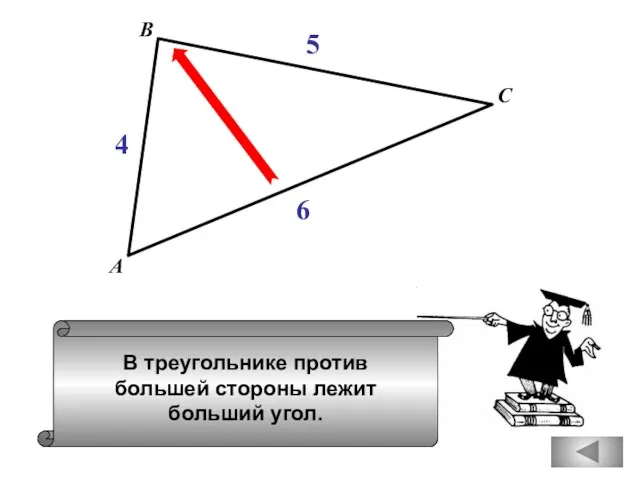
- 29. В треугольнике против большей стороны лежит больший угол. А В С 4 5 6
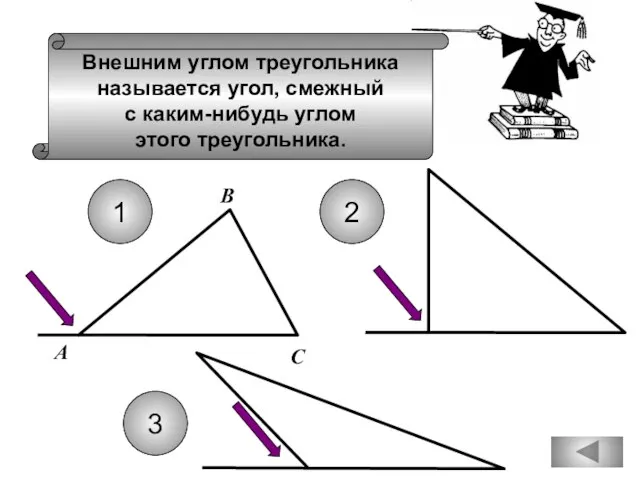
- 30. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. А В С 1 3
- 31. Каждая сторона треугольника меньше суммы двух других сторон. А В С
- 32. Какие из следующих утверждений верны? Задание 15 (№ 169921) 1 2 3 4 Если расстояние между
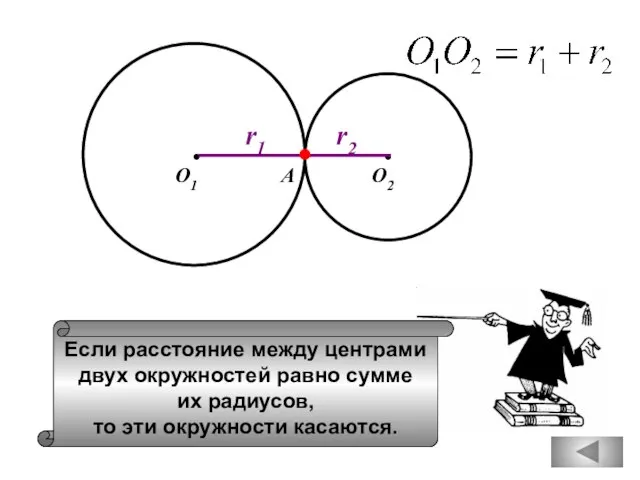
- 33. Если расстояние между центрами двух окружностей равно сумме их радиусов, то эти окружности касаются. О1 О2
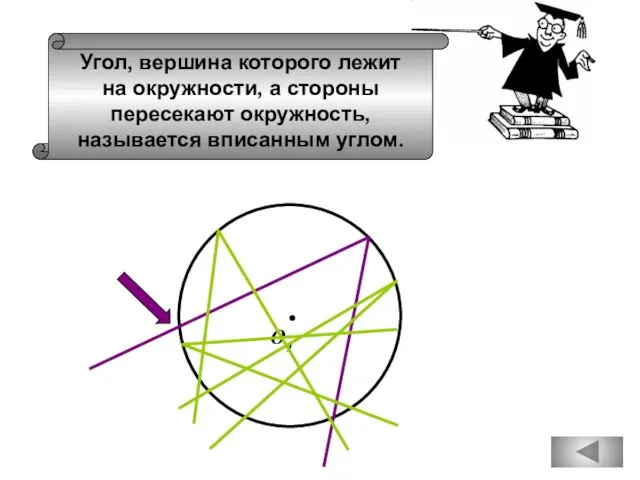
- 34. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. О1
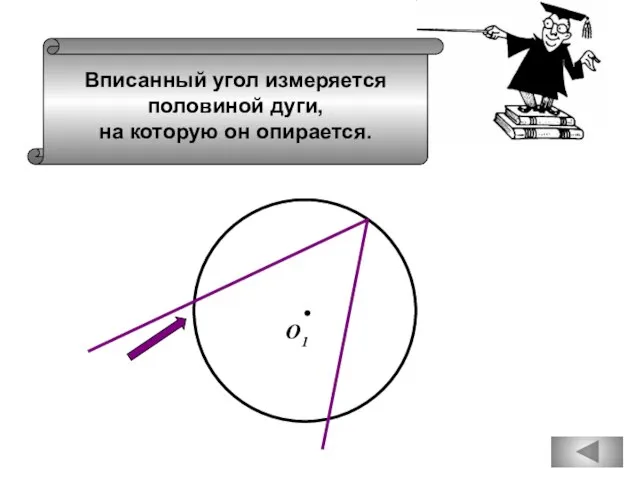
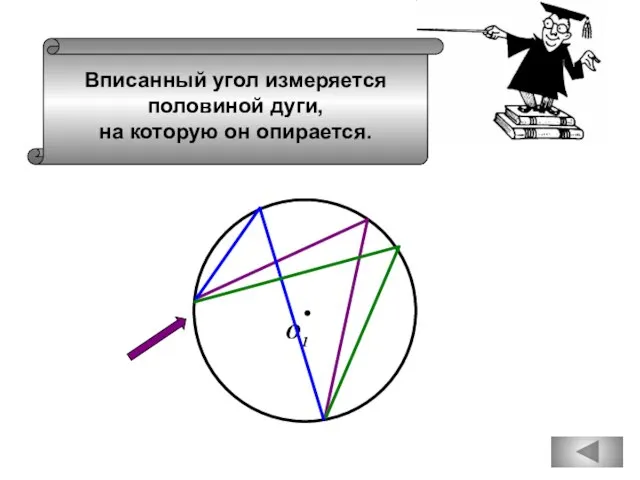
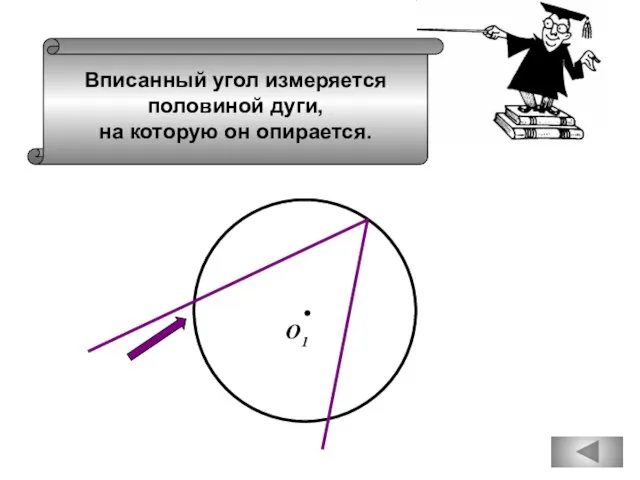
- 35. Вписанный угол измеряется половиной дуги, на которую он опирается. О1
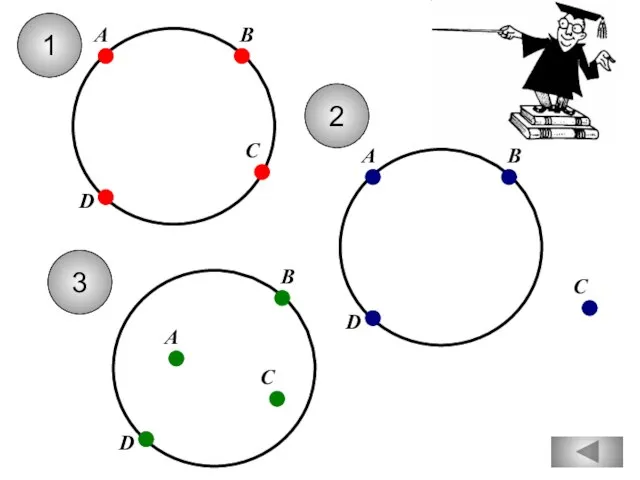
- 36. 1 С А В D 2 С А В D С А В D 3
- 37. Какие из следующих утверждений верны? Задание 15 (№ 169922) 1 2 3 4 Вписанные углы, опирающиеся
- 38. О1 Вписанный угол измеряется половиной дуги, на которую он опирается.
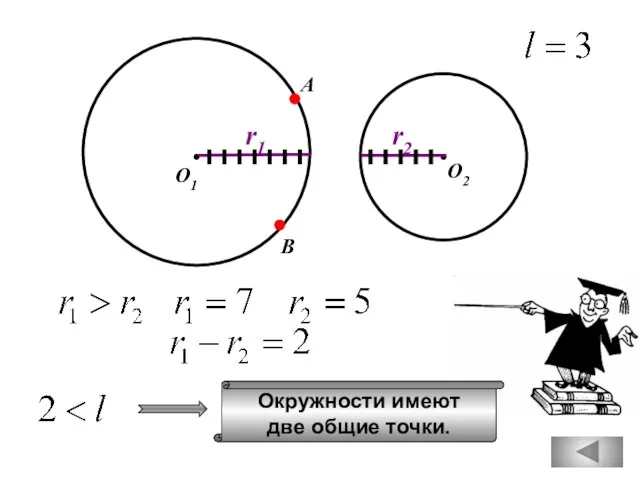
- 39. О1 О2 r1 r2 В А Окружности имеют две общие точки.
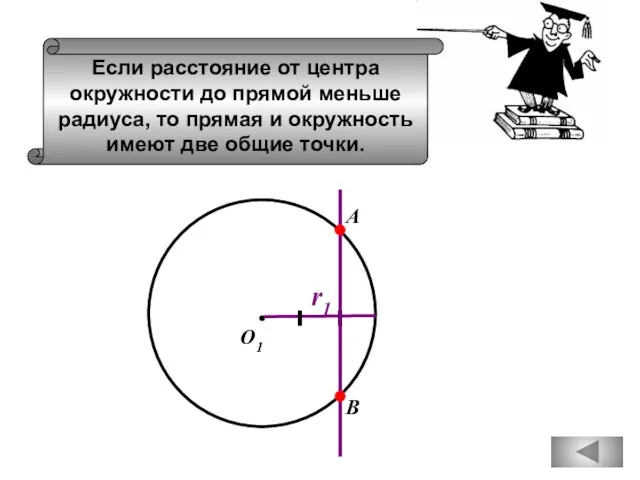
- 40. Если расстояние от центра окружности до прямой меньше радиуса, то прямая и окружность имеют две общие
- 41. Вписанный угол измеряется половиной дуги, на которую он опирается. О1
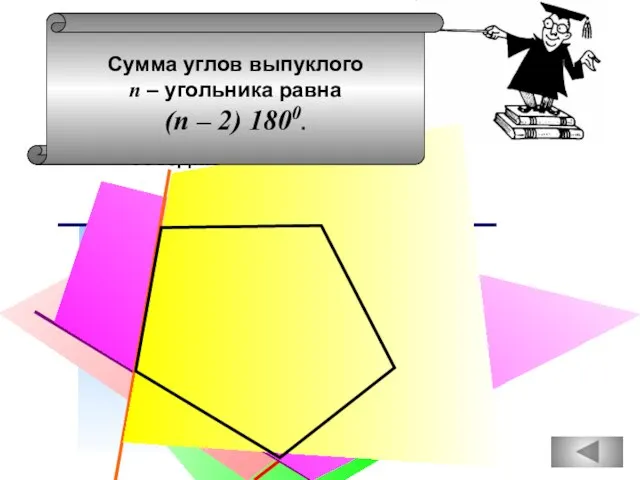
- 42. Какие из следующих утверждений верны? Задание 15 (№ 169924) 1 2 3 4 Сумма углов выпуклого
- 43. Прямоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его
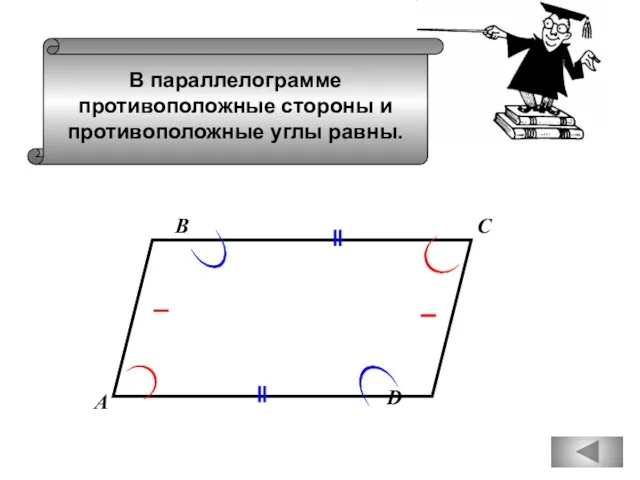
- 44. В параллелограмме противоположные стороны и противоположные углы равны. А С В D
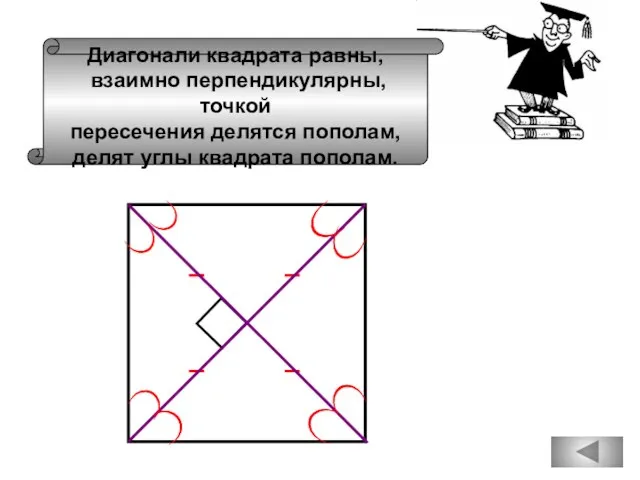
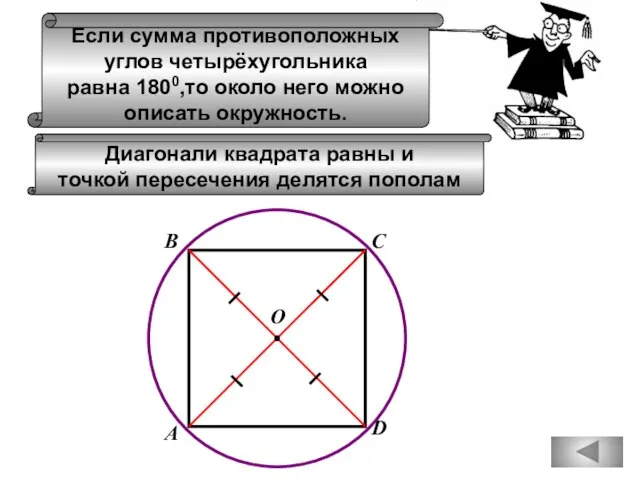
- 45. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам, делят углы квадрата пополам.
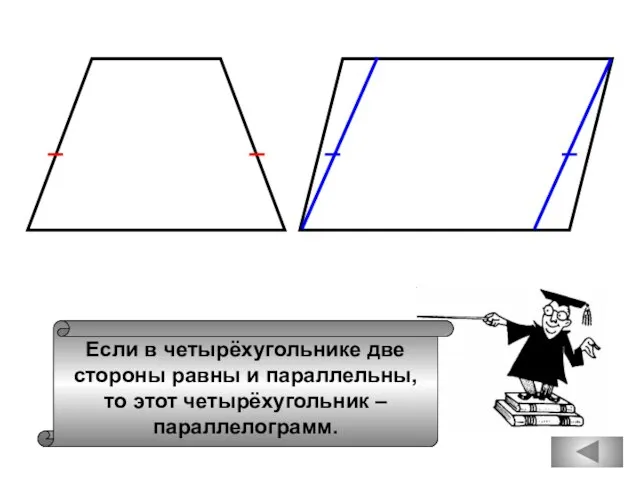
- 46. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- 47. Какие из следующих утверждений верны? Задание 15 (№ 169925) 1 2 3 4 Если противоположные углы
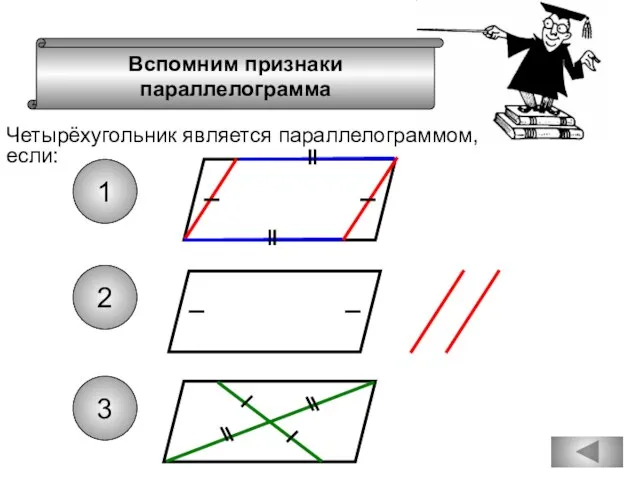
- 48. Вспомним признаки параллелограмма Четырёхугольник является параллелограммом, если: 1 2 3
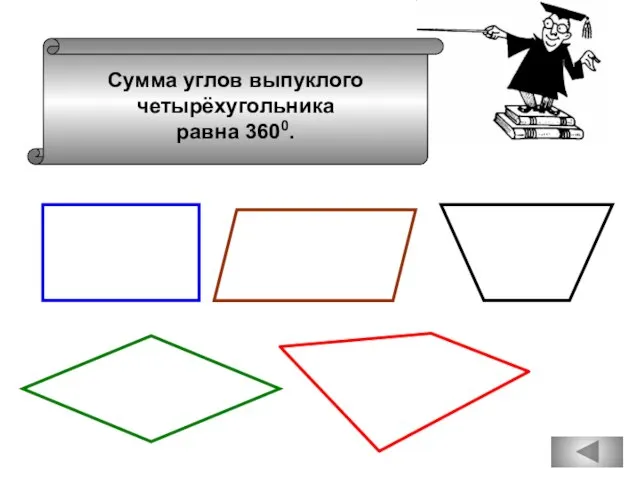
- 49. Сумма углов выпуклого четырёхугольника равна 3600.
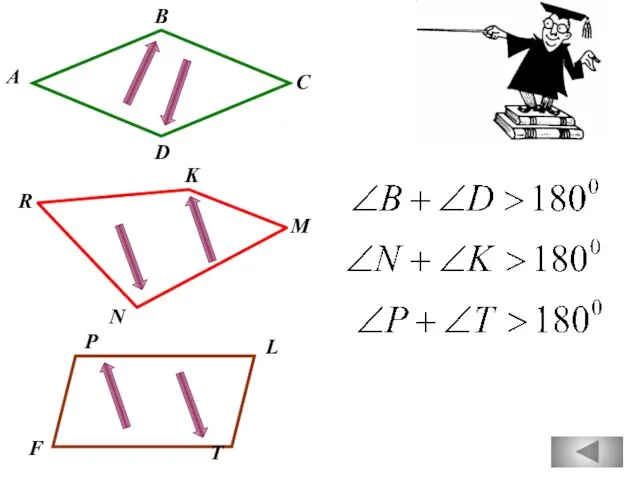
- 50. А В D С R N K M T F P L
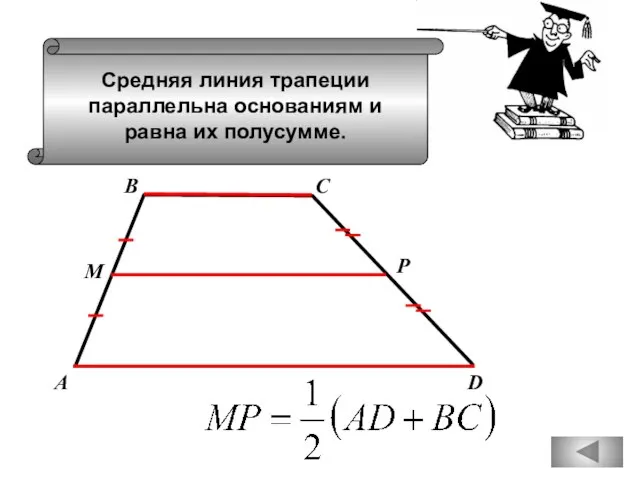
- 51. Средняя линия трапеции параллельна основаниям и равна их полусумме. А D В С М Р
- 52. Какие из следующих утверждений верны? Задание 15 (№ 169927) 1 2 3 4 Около любого ромба
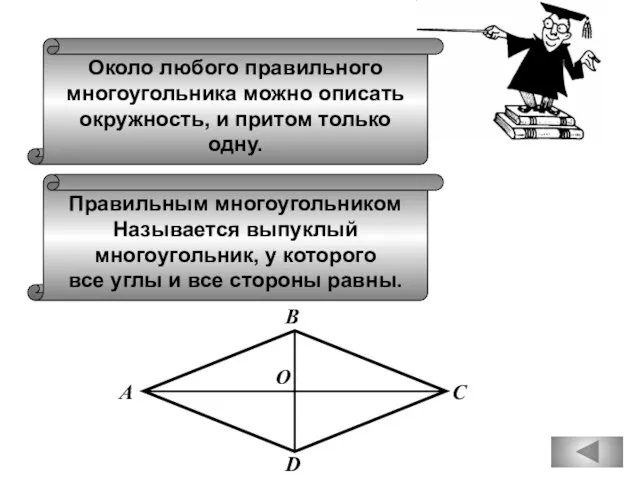
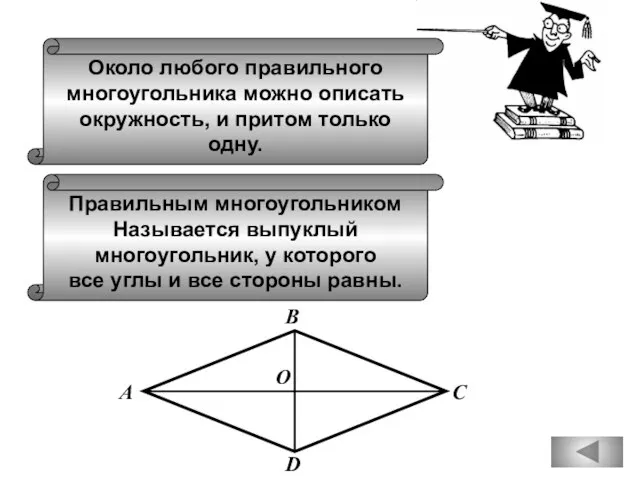
- 53. Около любого правильного многоугольника можно описать окружность, и притом только одну. Правильным многоугольником Называется выпуклый многоугольник,
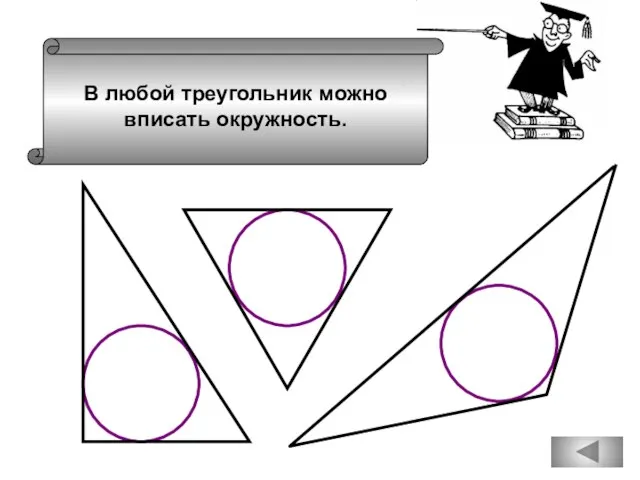
- 54. В любой треугольник можно вписать окружность.
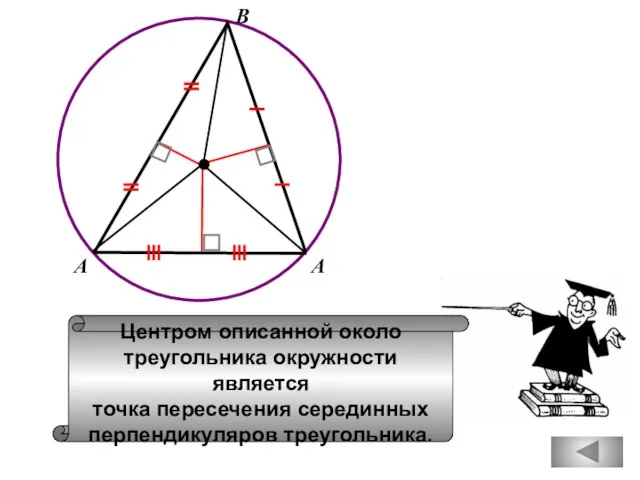
- 55. В Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника. А А
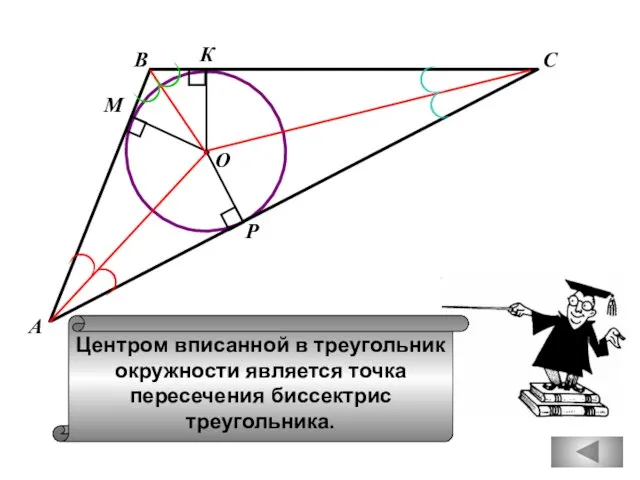
- 56. В С А М К Р Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
- 57. Какие из следующих утверждений верны? Задание 15 (№ 169929) 1 2 3 4 Около любого правильного
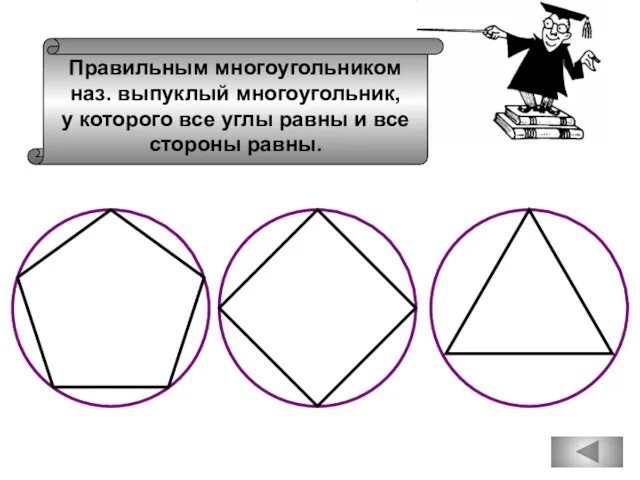
- 58. Правильным многоугольником наз. выпуклый многоугольник, у которого все углы равны и все стороны равны.
- 59. С А В
- 60. Если сумма противоположных углов четырёхугольника равна 1800,то около него можно описать окружность. А В С D
- 61. Около любого правильного многоугольника можно описать окружность, и притом только одну. Правильным многоугольником Называется выпуклый многоугольник,
- 62. Какие из следующих утверждений верны? Задание 15 (№ 169930) 1 2 3 4 Окружность имеет бесконечно
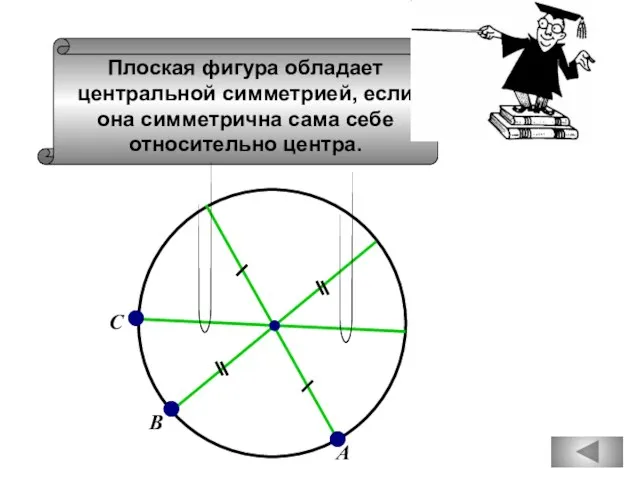
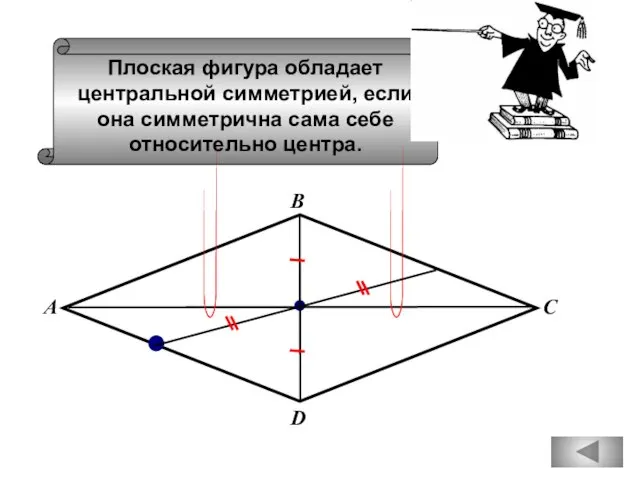
- 63. Плоская фигура обладает центральной симметрией, если она симметрична сама себе относительно центра. А С В
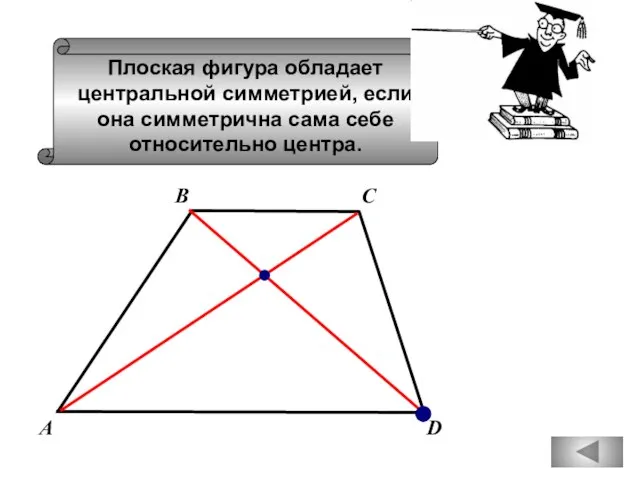
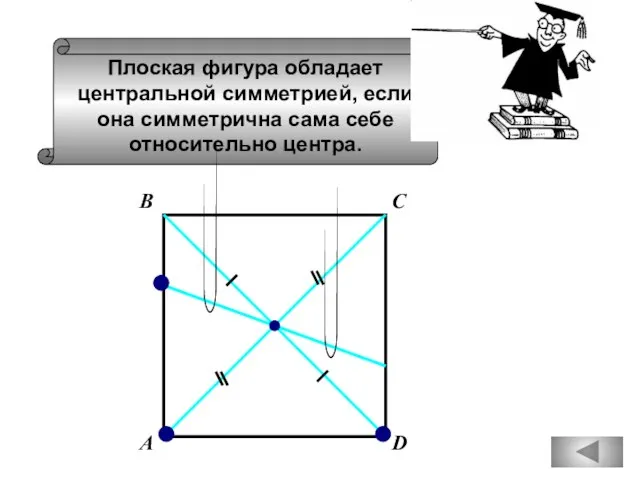
- 64. Плоская фигура обладает центральной симметрией, если она симметрична сама себе относительно центра. С В А D
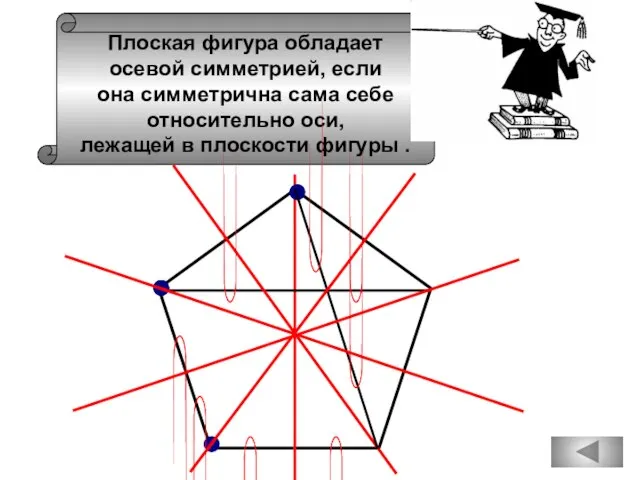
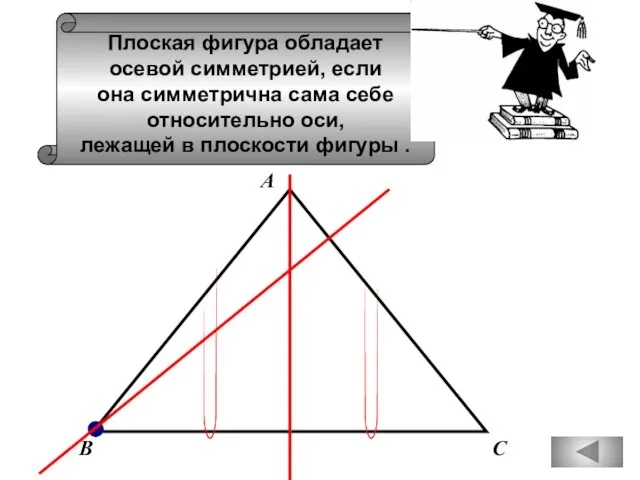
- 65. Плоская фигура обладает осевой симметрией, если она симметрична сама себе относительно оси, лежащей в плоскости фигуры
- 66. Плоская фигура обладает центральной симметрией, если она симметрична сама себе относительно центра. А С В D
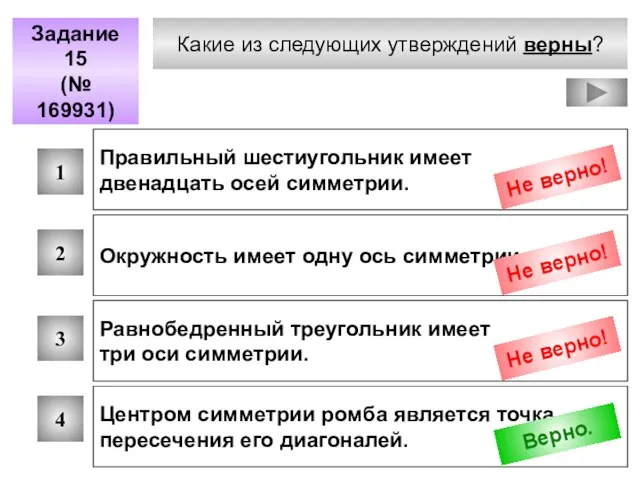
- 67. Какие из следующих утверждений верны? Задание 15 (№ 169931) 1 2 3 4 Правильный шестиугольник имеет
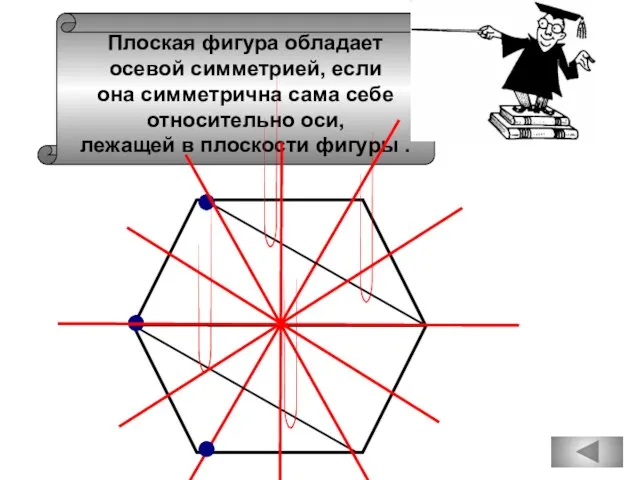
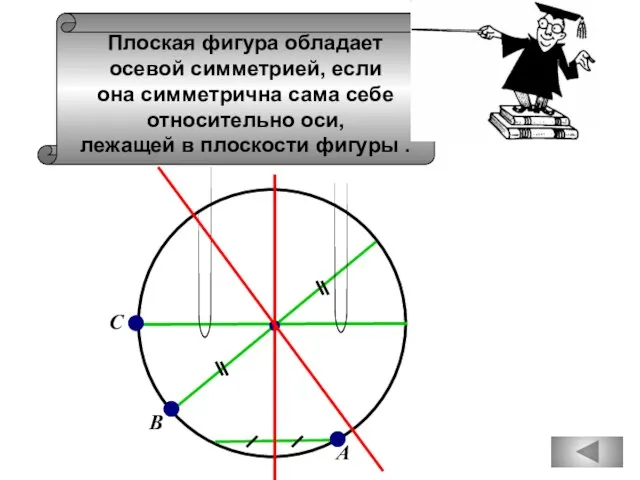
- 68. Плоская фигура обладает осевой симметрией, если она симметрична сама себе относительно оси, лежащей в плоскости фигуры
- 69. А С В Плоская фигура обладает осевой симметрией, если она симметрична сама себе относительно оси, лежащей
- 70. Плоская фигура обладает осевой симметрией, если она симметрична сама себе относительно оси, лежащей в плоскости фигуры
- 71. Плоская фигура обладает центральной симметрией, если она симметрична сама себе относительно центра. С В А D
- 72. Какие из следующих утверждений верны? Задание 15 (№ 169933) 1 2 3 4 Если катет и
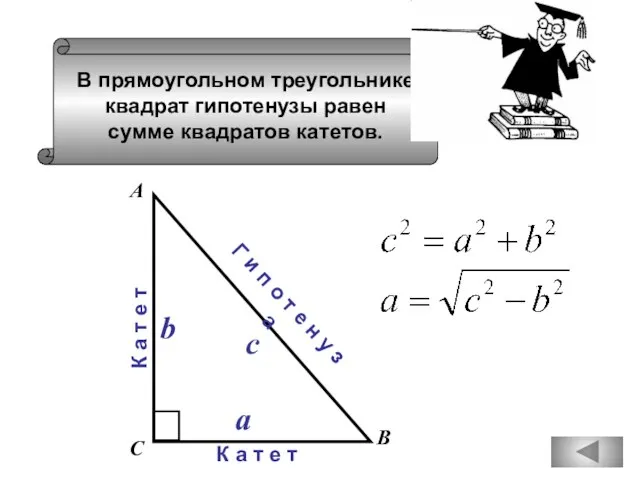
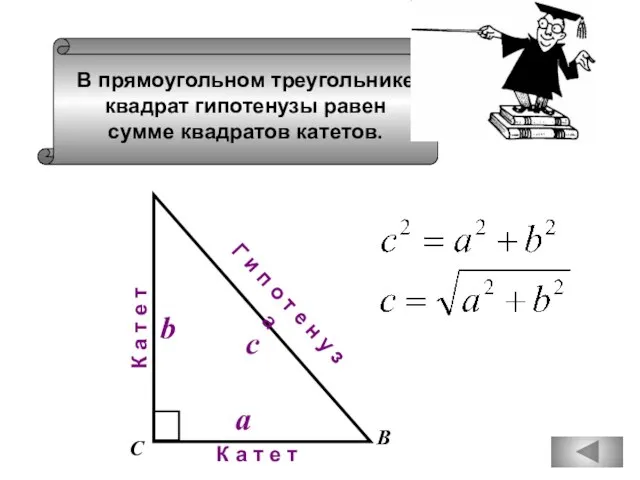
- 73. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А В С К а т е
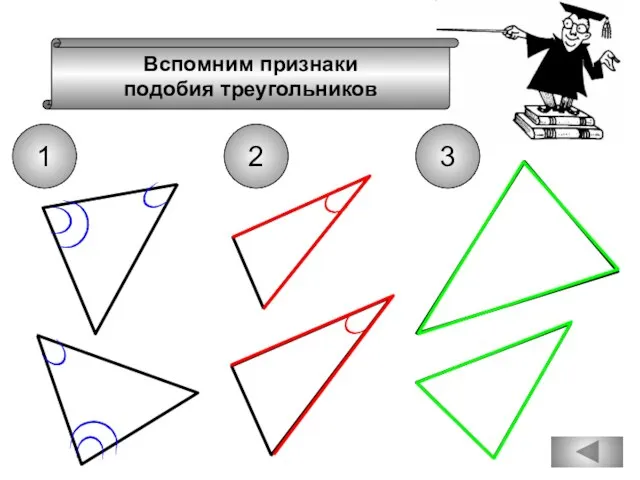
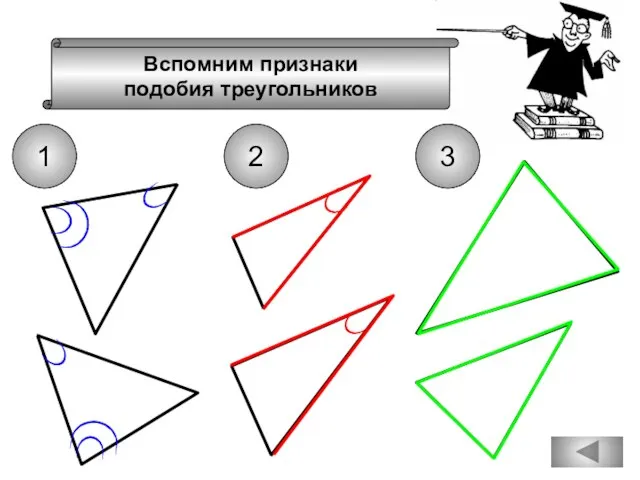
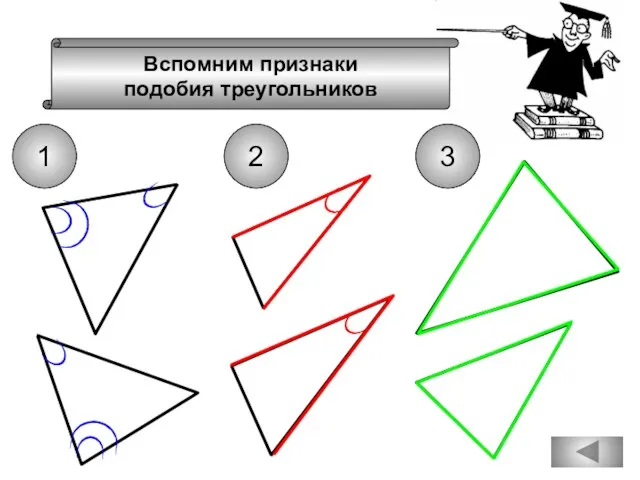
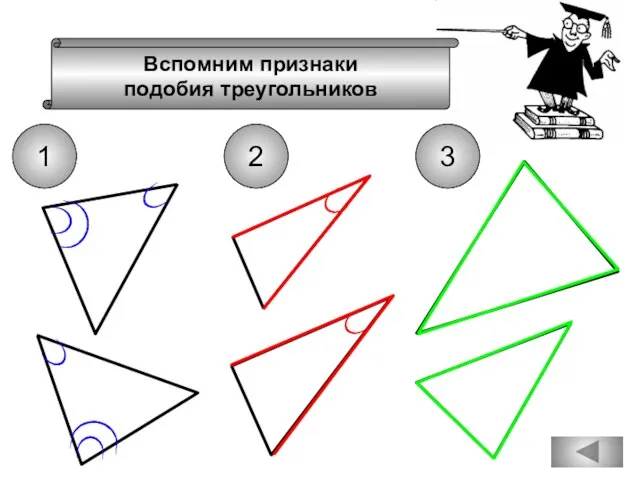
- 74. Вспомним признаки подобия треугольников 1 2 3
- 75. Вспомним признаки подобия треугольников 1 2 3
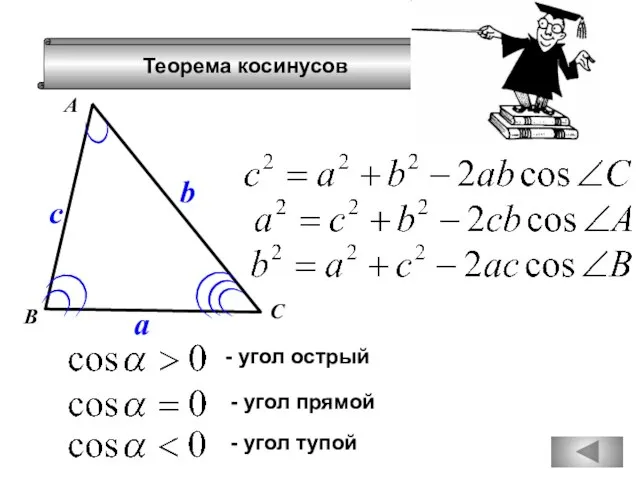
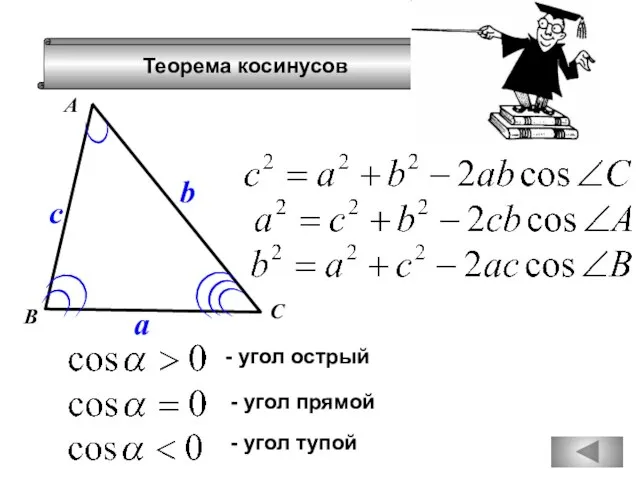
- 76. Теорема косинусов А В С a b c - угол острый - угол прямой - угол
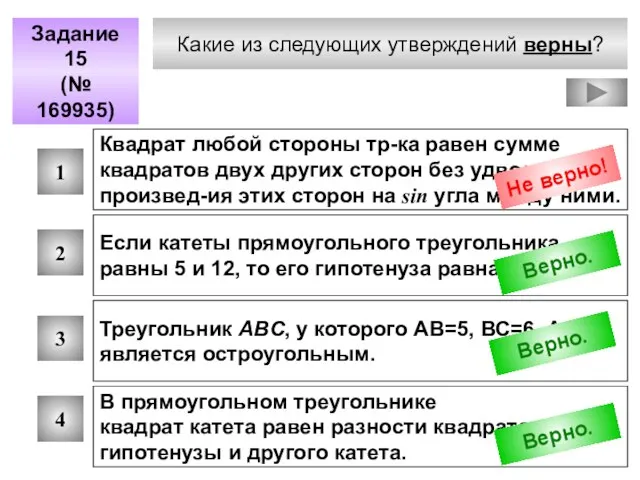
- 77. Какие из следующих утверждений верны? Задание 15 (№ 169935) 1 2 3 4 Квадрат любой стороны
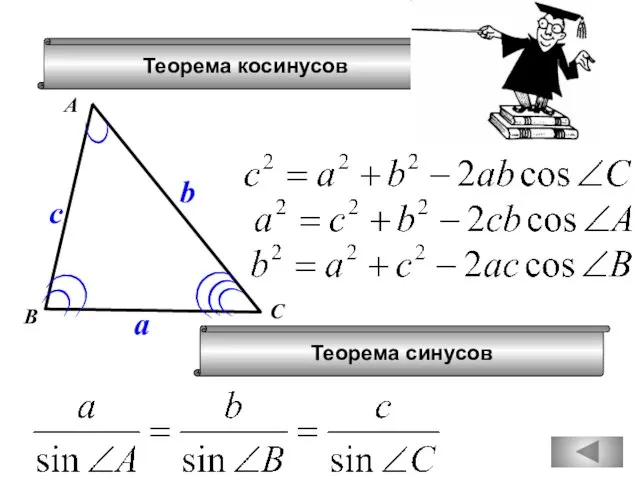
- 78. Теорема косинусов А В С a b c Теорема синусов
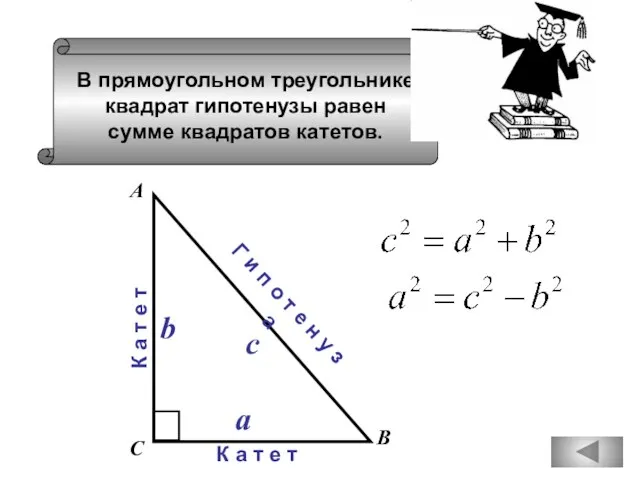
- 79. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В С К а т е т
- 80. Теорема косинусов А В С a b c - угол острый - угол прямой - угол
- 81. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А В С К а т е
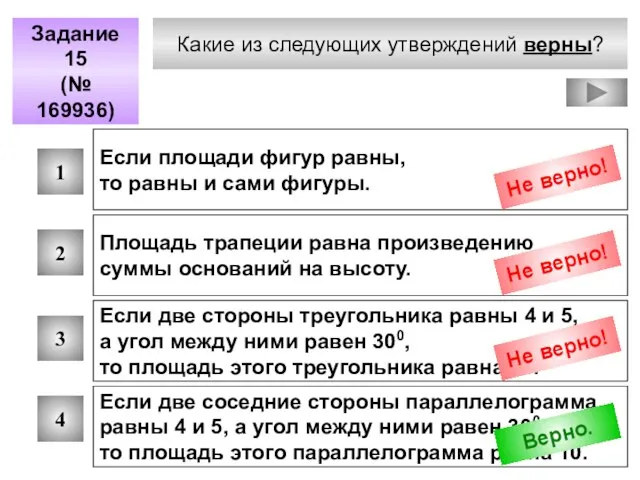
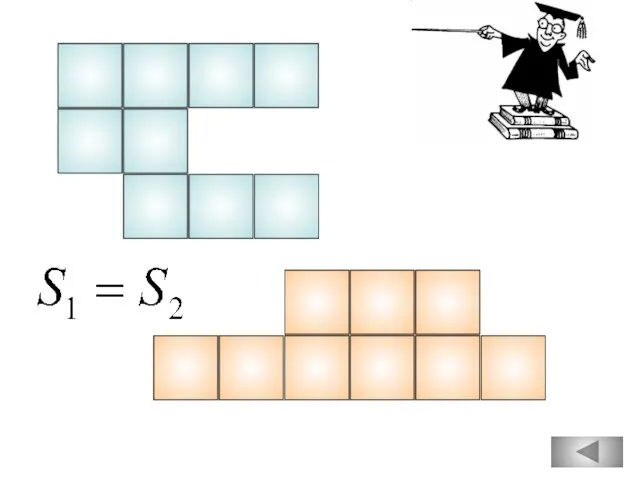
- 82. Какие из следующих утверждений верны? Задание 15 (№ 169936) 1 2 3 4 Если площади фигур
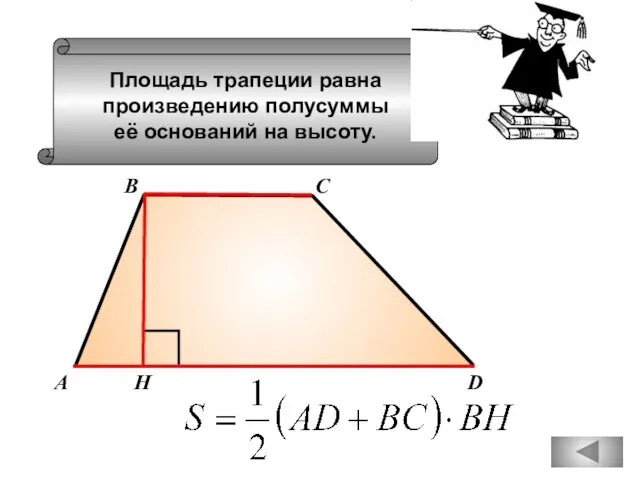
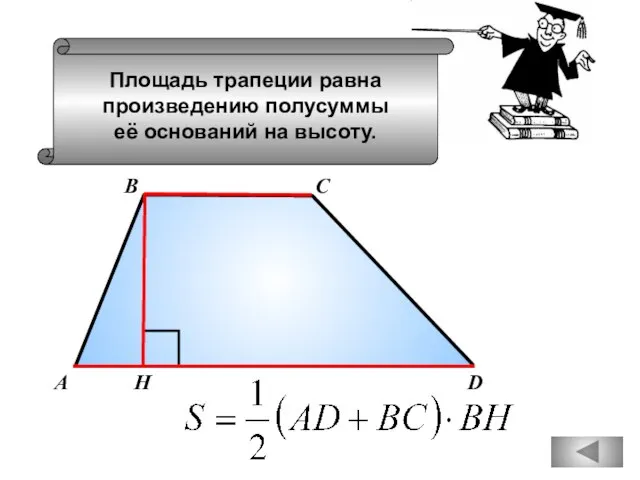
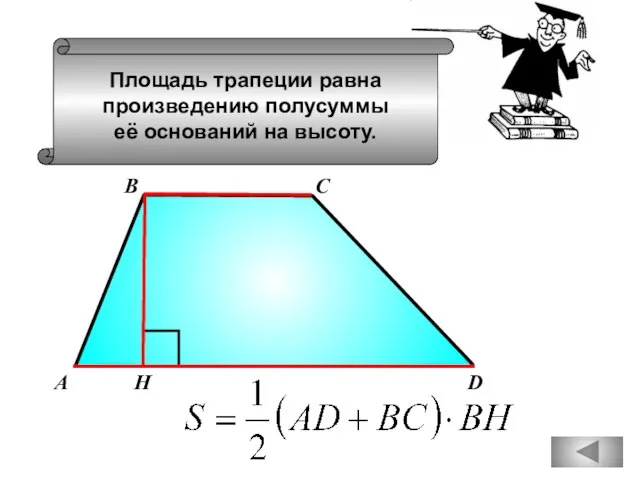
- 84. Площадь трапеции равна произведению полусуммы её оснований на высоту. А D В С Н
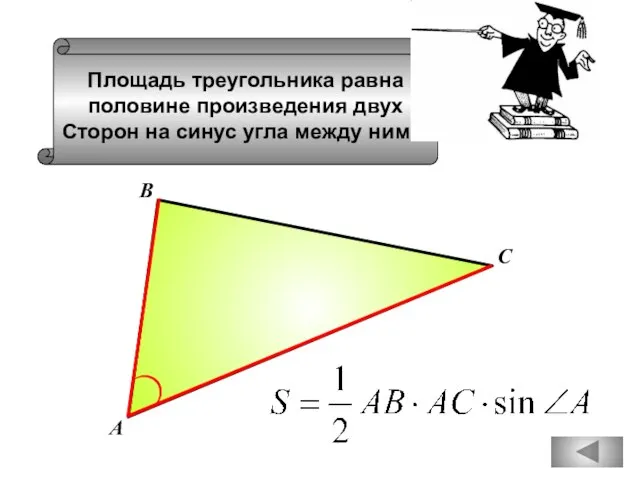
- 85. Площадь треугольника равна половине произведения двух Сторон на синус угла между ними. А В С
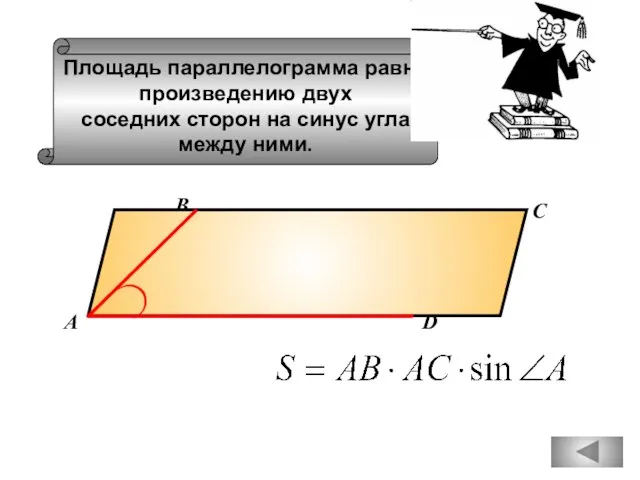
- 86. Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. А В С D
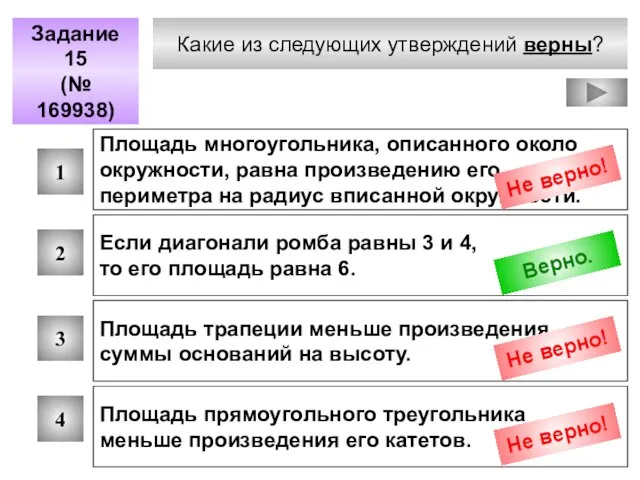
- 87. Какие из следующих утверждений верны? Задание 15 (№ 169938) 1 2 3 4 Площадь многоугольника, описанного
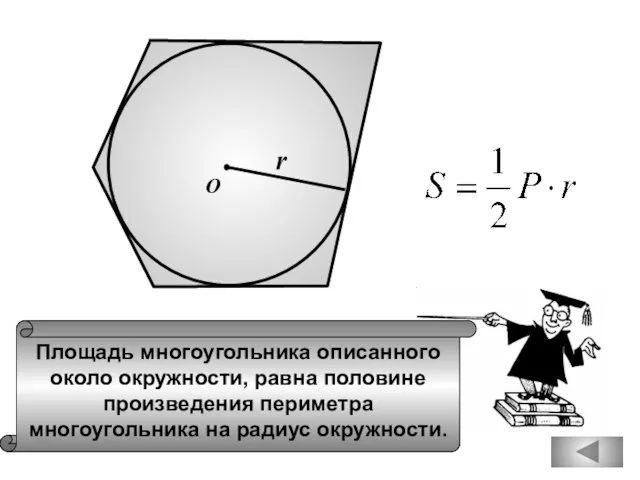
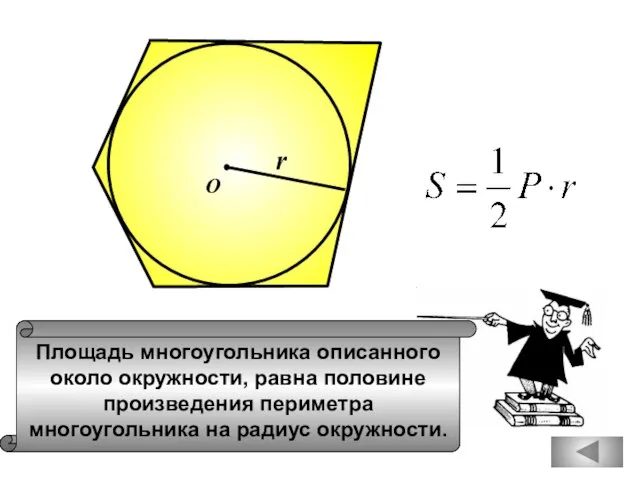
- 88. О r Площадь многоугольника описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
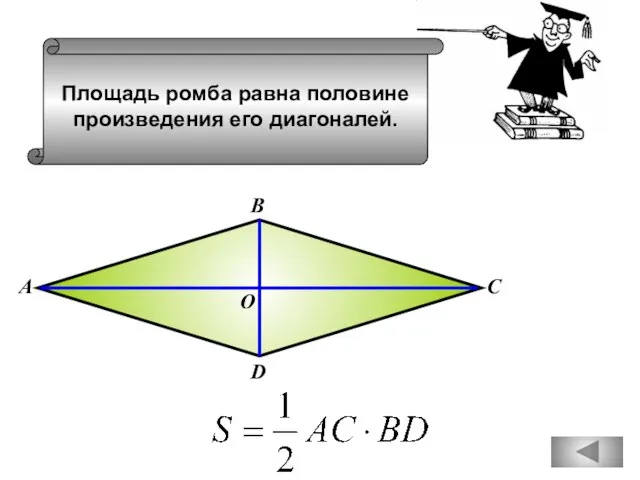
- 89. Площадь ромба равна половине произведения его диагоналей. В С А D О
- 90. Площадь трапеции равна произведению полусуммы её оснований на высоту. А D В С Н
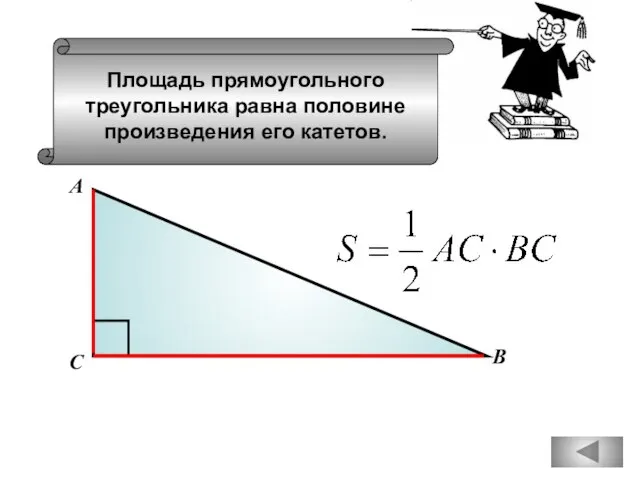
- 91. Площадь прямоугольного треугольника равна половине произведения его катетов. В С А
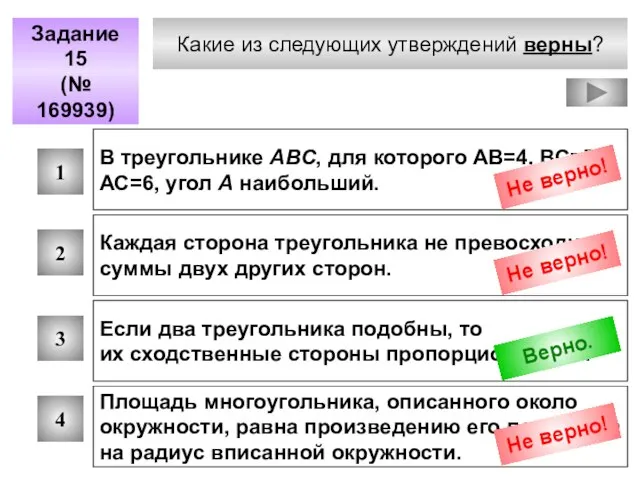
- 92. Какие из следующих утверждений верны? Задание 15 (№ 169939) 1 2 3 4 В треугольнике ABC,
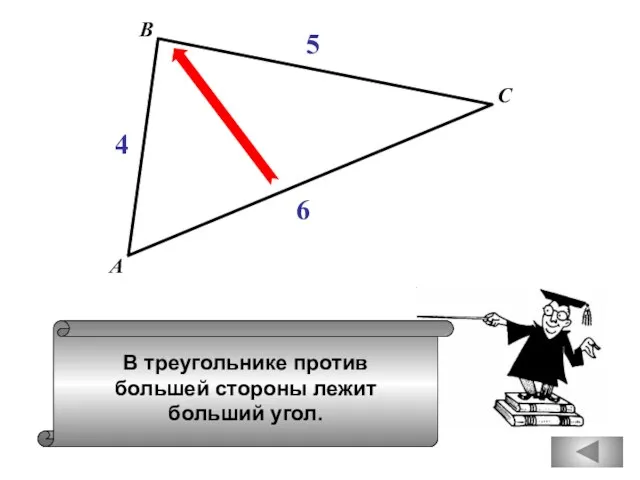
- 93. В треугольнике против большей стороны лежит больший угол. А В С 4 5 6
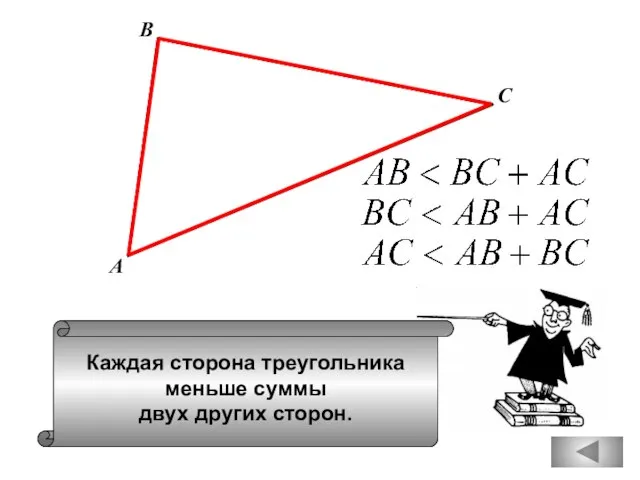
- 94. Каждая сторона треугольника меньше суммы двух других сторон. А В С
- 95. Вспомним признаки подобия треугольников 1 2 3
- 96. Площадь многоугольника описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности. О r
- 97. Какие из следующих утверждений верны? Задание 15 (№ 169941) 1 2 3 4 Если две стороны
- 98. Вспомним признаки подобия треугольников 1 2 3
- 99. В равнобедренном треугольнике углы при основании равны. А С М К Р
- 100. Площадь трапеции равна произведению полусуммы её оснований на высоту. А D В С Н
- 101. Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой
- 103. Скачать презентацию











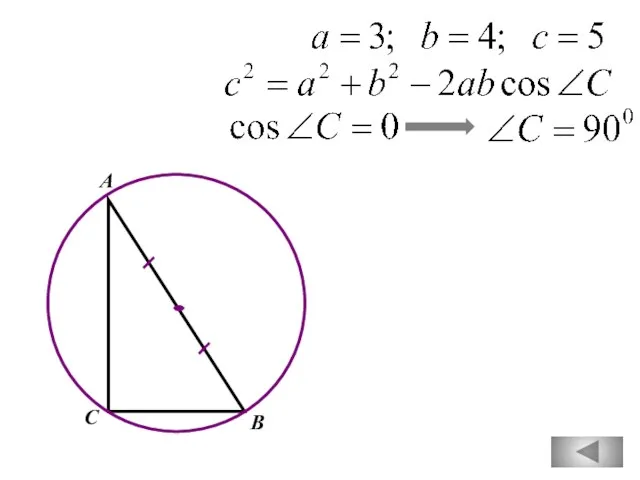



 Реформа языка Карамзина
Реформа языка Карамзина Варианты расчета бонуса за два месяца
Варианты расчета бонуса за два месяца Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Государство в политической системе
Государство в политической системе ИСТОРИЯ СПИЧЕК
ИСТОРИЯ СПИЧЕК Презентация на тему Растения-индикаторы
Презентация на тему Растения-индикаторы Мышление как психический процесс. Виды и формы мышления. 4 формата мышления
Мышление как психический процесс. Виды и формы мышления. 4 формата мышления Субъекты правовых отношений. Правовое положение лиц
Субъекты правовых отношений. Правовое положение лиц скульптура «Под одними звездами» ("Unter den gleichen Sternen")
скульптура «Под одними звездами» ("Unter den gleichen Sternen") Виды гимнастики
Виды гимнастики Hilton Hotels & Resorts
Hilton Hotels & Resorts Шар. Елка. Снеговик
Шар. Елка. Снеговик Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят Водные маршруты
Водные маршруты Презентация на тему Василий Тёркин
Презентация на тему Василий Тёркин  Технология приготовления пиццы
Технология приготовления пиццы Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В.
Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В. "Поле - чудес" по произведениям К.И. Чуковского
"Поле - чудес" по произведениям К.И. Чуковского PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha
PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha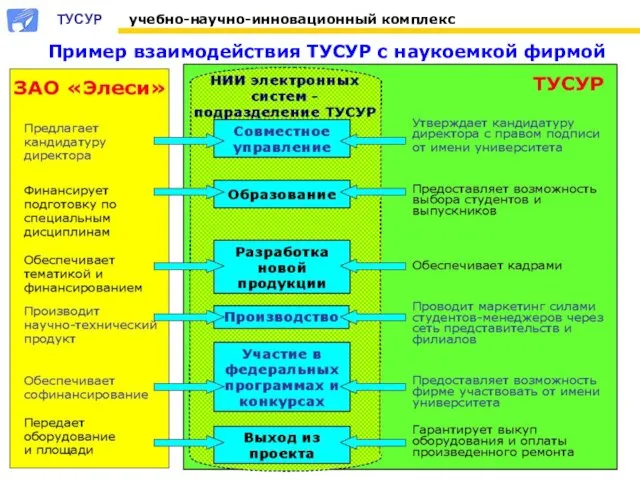 Пример взаимодействия ТУСУР с наукоемкой фирмой
Пример взаимодействия ТУСУР с наукоемкой фирмой Введение в менеджмент
Введение в менеджмент Австралия
Австралия Who should be the first ?
Who should be the first ? Велосипедный туризм
Велосипедный туризм Музей восстания машин
Музей восстания машин Презентация "Художники пореформенной России" - скачать презентации по МХК
Презентация "Художники пореформенной России" - скачать презентации по МХК Хочу отдыхать
Хочу отдыхать Сенситивные периоды человека (методика Марии Монтессори)
Сенситивные периоды человека (методика Марии Монтессори)