Содержание
- 2. Модуль «Алгебра» №1 Повторение (1) Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125
- 3. Повторение (подсказка) Чтобы перемножить десятичные дроби, надо умножать, не обращая внимания на запятую, а в полученном
- 4. Модуль «Алгебра» №1 Повторение (3) Вычислите значение выражения Ответ: 8.
- 5. Повторение (подсказка) Чтобы перемножить десятичную дробь и смешанное число, надо числа записать в каком-то одном виде.
- 6. Модуль «Алгебра» №1 Повторение (3) Вычислите значение выражения Ответ: 1,2.
- 7. Повторение (подсказка) Чтобы сократить дробь, можно «избавиться» от запятых. Для этого надо умножить числитель и знаменатель
- 8. Модуль «Алгебра» №1 Число 121,5 - наибольшее. Повторение (4) Укажите, какое из следующих выражений принимает наибольшее
- 9. Повторение (подсказка) Если числитель дроби меньше знаменателя, то дробь называется правильной, и ее целая часть равна
- 10. Модуль «Алгебра» №1 Повторение (3) Расположите в порядке возрастания: Ответ: ⎕ ⎕ ⎕ ⎕
- 11. Повторение (подсказка) Чтобы привести дроби к общему знаменателю (желательно к наименьшему), надо найти НОК знаменателей дробей,
- 12. Модуль «Алгебра» №1 Повторение (2) Сопоставьте числовые выражения и принимаемые ими значения: Ответ: Числовые выражения: Значения:
- 13. Повторение (подсказка) Чтобы число умножить на сумму, надо это число умножить на каждое слагаемое. Чтобы из
- 14. Модуль «Алгебра» №1 Повторение (4) Запишите в ответ номера неверных равенств: Ответ: 124 Рав-во неверное ⇒
- 15. Повторение (подсказка) Квадрат числа можно вычислить следующим образом: а² = а ∙ а. Произведение взаимно обратных
- 16. Модуль «Алгебра» №1 Повторение (5) Запишите в ответе номера выражений, значения которых равны 0: Ответ: 14
- 17. Повторение (подсказка) Четная степень отрицательного числа дает «положительный» результат. Нечетная степень отрицательного числа дает «отрицательный» результат.
- 18. Модуль «Алгебра» №1 Повторение (4) Ответ: 235. Запишите в ответе номера выражений, значения которых меньше 0:
- 19. Повторение (подсказка) Если в дробях одинаковые числители, то та дробь больше, у которой знаменатель меньше. Если
- 21. Скачать презентацию


















 Викторина. Мультфильмы
Викторина. Мультфильмы Хохломская роспись
Хохломская роспись Войска, не входящие в министерство обороны РФ, их назначение
Войска, не входящие в министерство обороны РФ, их назначение Страховое дело. Лекция 3
Страховое дело. Лекция 3 Нам песня жить помогает - юбилейный тур Хора ветеранов Мытищинского дворца культуры Яуза по городам Подмосковья
Нам песня жить помогает - юбилейный тур Хора ветеранов Мытищинского дворца культуры Яуза по городам Подмосковья Биосферный центральный заповедник
Биосферный центральный заповедник The state system of Great Britain
The state system of Great Britain Гробницы эпохи Нового царства
Гробницы эпохи Нового царства Where are you from
Where are you from Технология монтажа и подключения к сети светильников с люминесцентными лампами
Технология монтажа и подключения к сети светильников с люминесцентными лампами Математика в архитектуре.Древней Греции и средних веков
Математика в архитектуре.Древней Греции и средних веков Кто и когда изобрел бумагу?
Кто и когда изобрел бумагу? Презентация на тему Золотое сечение - божественная мера красоты
Презентация на тему Золотое сечение - божественная мера красоты  Здоровая пища (1 класс)
Здоровая пища (1 класс) Как же сформировать положительную мотивацию при обучении математике? Этот компонент имеет настолько боль
Как же сформировать положительную мотивацию при обучении математике? Этот компонент имеет настолько боль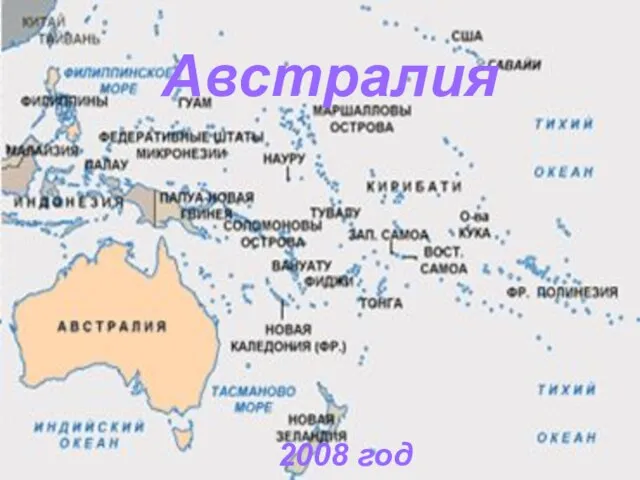 Австралия
Австралия Необитаемый остров
Необитаемый остров Устройства компьютера
Устройства компьютера Презентация на тему Витус Беринг
Презентация на тему Витус Беринг  РЕНТГЕНОВСКАЯ ТОМОГРАФИЯ
РЕНТГЕНОВСКАЯ ТОМОГРАФИЯ Международный Олимпийский комитет
Международный Олимпийский комитет Загрязнения водоёмов
Загрязнения водоёмов Кулинарная студия для детей. Овощи
Кулинарная студия для детей. Овощи Сталинградская битва(17 июля 1942 – 2 февраля 1943)
Сталинградская битва(17 июля 1942 – 2 февраля 1943) Энергоэффективные технологии и способы их внедрения в системы ЖКХ города
Энергоэффективные технологии и способы их внедрения в системы ЖКХ города Кафедра Загальної Фізики
Кафедра Загальної Фізики Barrier Ownership Overview
Barrier Ownership Overview 1 декабря – Всемирный день борьбы со СПИДом.
1 декабря – Всемирный день борьбы со СПИДом.