Гидродинамика Солнца

Ранние исследования тепловой конвекции
Середина XVIII в. ― М. В. Ломоносов, Дж. Гадлей (G. Hadley); качественное объяснение природы явления
1900 ― А. Бенар (H. Bénard), эксперимент
1906 ― K. Schwarzschild, условие возникновения
1916 ― лорд Рэлей (Rayleigh), теория
1930–1950 ― H. Siedentopf и др., теория пути перемешивания
1940 ― A. Pellew & R. Southwell, линейная теория
1961 ― С. Чандрасекар (S. Chandrasekhar); линейная теория, первая фундаментальная монография

Шестиугольные ячейки (Бенара)

Квазидвумерные конвективные валы (convection rolls)

Уравнение Навье – Стокса
(the Navier–Stokes equation)
Вязкий тензор напряжений:

Уравнение Навье – Стокса
(the Navier–Stokes equation)
Если коэффициенты постоянны:

Баротропность и бароклинность
В состоянии равновесия
Баротропность:
Бароклинность:

Уравнение непрерывности. Несжимаемая жидкость
в поле тяжести

Приближение Буссинеска (the Boussinesq approximation)

Уравнение переноса тепла
В несжимаемой среде (сp = сv)
с постоянной теплопроводностью:

Полная система уравнений приближения Буссинеска

Обобщение приближения Буссинеска на случай
сжимаемой среды
Spiegel & Veronis (1960):
Для исследования движений с конечной амплитудой
― дополнительно:

Задача
Рэлея ― Бенара

Задача Рэлея ― Бенара
(the Rayleigh–Bénard problem)
Горизонтальный слой 0 ≤ z ≤ h TS = T1 – βz
T = T1 при z = 0
T = T2 = T1 – ΔT при z = h

Безразмерная форма уравнений
Безразмерные параметры задачи:

Постановка стандартной задачи

Линейный анализ

Поиск собственных функций (eigenfunctions)

Функции планформы
Валы:
Шестиугольники:

Краевая задача (boundary-value problem) для функции f

Собственные значения (eigenvalues) и собственные функции в случае свободных границ (stress-free boundaries)

Нейтральная кривая задачи Рэлея ― Бенара

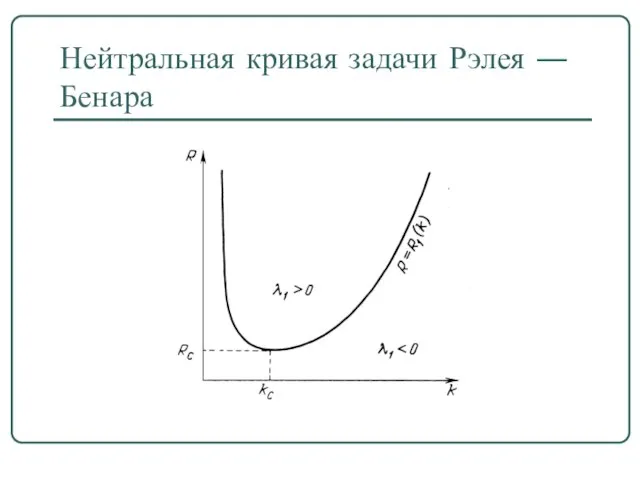
Критические числа Рэлея и волновые числа

Структуры конвективных течений

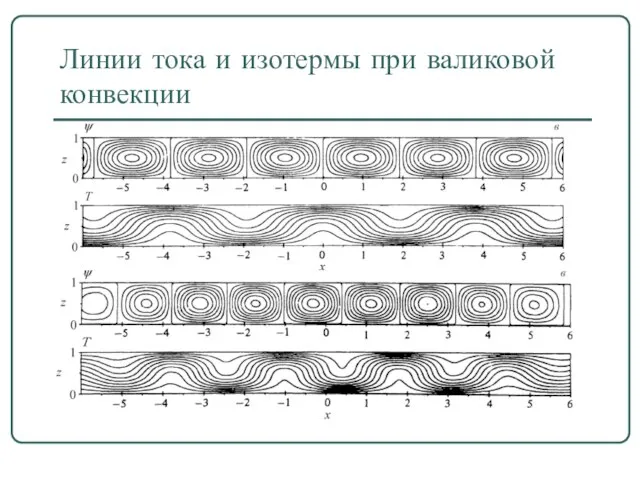
Шестиугольные ячейки (Бенара)

Квазидвумерные конвективные валы

Линии тока и изотермы при валиковой конвекции

Сценарии эволюции шестиугольных ячеек
Слой с жесткими границами

Сценарии эволюции шестиугольных ячеек
Слой с жесткими границами

Литература
Л.Д. Ландау, Е.М. Лифшиц. Гидродинамика, 3-е изд. М: Физматлит, 1986.
Дж. Бэтчелор. Введение в динамику жидкости, М.: Мир, 1973.
С.Б. Пикельнер. Основы космической электродинамики, 2-е изд. М:Физматлит, 1966.
А.В. Гетлинг. Конвекция Рэлея–Бенара. Структуры и динамика. М: УРСС, 1999.