Гиперболоид

Определение однополостного гиперболоида
Однополостным гиперболоидом называется поверхность второго порядка, которая в канонической системе координат определяется уравнением
.
Оси канонической системы координат являются осями симметрии однополостного гиперболоида, начало координат – его центром симметрии, а координатные плоскости – плоскостями симметрии. Оси абсцисс и ординат пересекают однополостный гиперболоид в точках A1(−a; 0; 0), A2(a; 0; 0), B1(0; −b; 0), B2(0; b; 0), которые называются его вершинами. Ось аппликат Oz, не имеющая с гиперболоидом общих действительных точек, называется его мнимой осью.

Если рассмотреть сечения однополостного гиперболоида (16) плоскостью xOy: z = 0 или плоскостями, параллельными ей (z = h3), то в сечении получаются эллипсы. Эллипс
называется горловым.
Теперь возьмем сечение однополостного гиперболоида плоскостью xOz: y = 0. Оно задается системой уравнений
и представляет собой гиперболу с действительной осью Ox:
.

Рассматривая аналогично сечения гиперболоида плоскостью yOz: x = 0, а также плоскостями, параллельными плоскостям xOz: y = h2 и yOz: x = h1, получаем кривые второго порядка гиперболического типа. Это – либо гипербола (при |h1| ≠ a, | h2| ≠ b), либо пара пересекающихся прямых (при |h1| = a, | h2| = b). Например, сечение однополостного гиперболоида плоскостью x = a задается системой уравнений
и представляет собой пару пересекающихся прямых с каноническим уравнением

Однополостный гиперболоид

Однополостный гиперболоид

Сечение однополостного гиперболоида

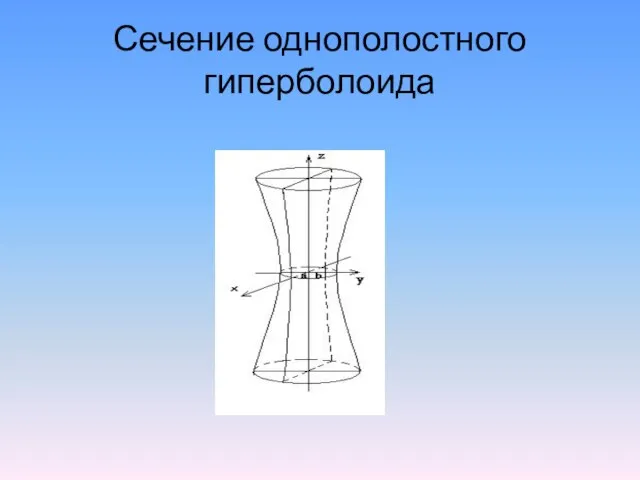
Определение двуполостного гиперболоида
Двуполостным гиперболоидом называется поверхность второго порядка, которая в канонической системе координат определяется уравнением
.
Ось аппликат Oz канонической системы координат является осью симметрии двуполостного гиперболоида, начало координат – его центром симметрии, а координатные плоскости – плоскостями симметрии. Ось аппликат пересекает гиперболоид в точках C1(0; 0; −c), C2(0; 0; c) которые называются его вершинами. Сама ось аппликат называется действительной осью гиперболоида.

Если рассмотреть сечение двуполостного гиперболоида координатными плоскостями xOz: y = 0 и yOz: x = 0, и плоскостями, им параллельными (x = h1, y = h2), то в сечении получаются гиперболы.
Рассматривая аналогично сечения гиперболоида плоскостью xOy: z = 0, а также плоскостями, параллельными плоскости xOy: z = h, получаем кривые второго порядка эллиптического типа. Это – либо эллипс (при |h| > c), либо пара мнимых пересекающихся прямых, т.е. точка (при |h = c |), либо мнимый эллипс (при |h| < c). Например, при |h| > c сечение двуполостного гиперболоида плоскостью z = h задается системой уравнений
откуда при подстановке второго уравнения в первое последовательно получаем:
и каноническое уравнение эллипса

Двуполостный гиперболоид

Двуполостный гиперболид