Глава 3. Стили функционального программирования

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Основные примитивные функции в ЛИСПе
Арифметические и логические функции: PLUS, MULT, LE, EQ, AND
Специальные функции: COND, QUOTE, LET
Функции обработки списков: CAR, CDR, CONS
(CONS 'A '(B C)) ? (A B C)
(CONS 'A (CONS 'B NIL)) ? (A B)
(CAR '(A B C)) ? A
(CDR '(A B C)) ? (B C)
(CDR '(A)) ? NIL
(CONS '(A B) '(C D)) ? ((A B) C D)
(CAR (CDR '(A B C D))) ? B
(CADDR '(A B C D))) ? C
(CONS 'LAMBDA (CONS '(X) '((PLUS X 1)))) ? (LAMBDA (X) (PLUS X 1))
Функции высших порядков в ЛИСПе:
(DEFINE MAP (LAMBDA (F L)
(COND (L (CONS (F (CAR L)) (MAP F (CDR L))))
(T NIL)
)))
(MAP '(LAMBDA (X) (PLUS X 1)) '(1 3 8)) ? (2 4 9)

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Функции как значения
Функциональное значение – это либо встроенная функция, либо список, первым атомом которого является специальный атом LAMBDA. Например,
(LAMBDA (X) (MULT 2 X))
Если функция применяется к аргументу, то формальные параметры «связываются» со значением аргумента, поэтому, например, выражение
((LAMBDA (X) (MULT 2 X)) 3)
при вычислении выдает значение 6.
Как происходит вычисление, если в теле функции используются «глобальные» атомы?
(LAMBDA (X) (MULT Y X))
Два возможных подхода:
статический: значения «глобальных» атомов фиксируются в момент определения функции (в момент «исполнения» функции LAMBDA).
динамический: значения «глобальных» атомов определяются во время работы функции.
Разница может проявиться, если функция определена в одном контексте, а исполняется в другом.
В некоторых (старых) версиях ЛИСПа для «фиксации» контекста применялись специальные функции, например, если лямбда-выражение передавалось в качестве аргумента в другую функцию, то можно было использовать специальную функция FUNCTION вместо QUOTE.

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Подведение итогов: основные черты и особенности языка ЛИСП
Простой синтаксис – скобочная запись данных и программ.
Энергичная схема вычислений (кроме специальных функций).
Нет образцов и конструкторов – определение функций построено на суперпозиции примитивных и ранее определенных функций; построение сложных объектов также использует функцию CONS.
Возможность определения функций высших порядков, в которых аргументами и/или результатом работы являются функции.
Возможность динамического построения фрагментов программы непосредственно в ходе ее выполнения.
Определение «контекста переменных» с помощью блочной структуры (LET).
Язык ЛИСП послужил прообразом и идейной основой большой группы языков. В той или иной степени он лежит в основе всех современных функциональных языков программирования и многих других языков.

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
3.2. Система комбинаторного программирования FP (John Backus, 1978)
Теоретически любую функцию можно получить из базовых с помощью комбинаторных преобразований. FP – система, реализующая этот принцип.
Набор констант не определен, но предполагается, что есть списки и логические значения.
Набор базовых функций не определен, но предполагается, что он достаточно богат.
Также предполагается, что принята энергичная схема вычислений (все функции – строгие).
Определим следующие комбинаторы:
Композиция f ◦ g
(f ◦ g) x = f (g x)
Условие f → g; h
(f → g; h) x =
Константа k
k x =
Конструкция [f1, f2,..., fn]
[f1, f2,..., fn] x =
{
g x, если f x - истинно
h x, если f x - ложно
не опр., если f x – не определено
{
k, если x – определено
не опр., если x – не определено

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Еще несколько важных комбинаторов
Отображение α f
(α f) :
=
Правая вставка / f
(/ f) :
= x
(/ f) :
= f :
>
Левая вставка \ f
(\ f) :
= x
(\ f) :
= f : <(\ f) :
, xn>
(map)
(foldr1)
(foldl1)
Вариант правой вставки с базовой константой /k f
(/k f) : <> = k
(/k f) :
= f :
>
Вариант левой вставки с базовой константой \k f
(\k f) : <> = k
(\k f) :
= f : <(\k f) :
, xn>
(foldr)
(foldl)

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Определим типичный язык программирования на основе FP-системы
Введем набор констант и базовых функций
Константы:
Функции:
Арифметические функции: +, -, *, add1, mul5, sub3:
+ : <2,5> = 7
add1 : 3 = 4
Логические функции: =, /=, <, >,..., and, or, not,... eq0, neq5, lt2:
= : <2,5> = F
< : <3,4> = T
lt2 : 5 = T
or :
= T
Функции-селекторы: 1, 2,..., 1r, 2r,...:
2 : <2,5,7> = 5
1r : <3,4,8> = 8
Тождественная функция: id:
id : <3,5> = <3,5>
в программах в явном виде не присутствуют!
гетерогенные списки (<>, <1, <1, 2>, T>,…)
целые числа (0, 1, 2,..., -1, -2,...);
логические значения (T и F);
символы ('s', '*',…);

hd : <3,5,8> = 3
Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Функции обработки списков
tl : <3,5,8> = <5,8>
hr : <3,5,8> = 8
tr : <3,5,8> = <3,5>
cons : <3, <5,4>> = <3,5,4>
consr : <<5,4>, 3> = <5,4,3>
null : <> = T
null : <3,5> = F
distl : <3, <1,2,5>> = <<3,1>, <3,2>, <3,5>>
distr : <<1,2,5>, 3> = <<1,3>, <2,3>, <5,3>>
ι : 5 = <1,2,3,4,5>
ι : 0 = <>
Программа в FP – это определение функций:
def sqr = * ◦ [id, id]
sqr : 5 = * : <5, 5> = 25
def pow4 = * ◦ [sqr, sqr]
pow4 : 3 = * :
= 81

Кубенский А.А. Функциональное программирование.
Глава 3. Стили функционального программирования.
Примеры программ в языке программирования на базе FP
Haskell: fact n = if n = 0 then 1 else n * fact (n-1)
FP: def fact = eq0 → 1; (* ◦ [id, fact ◦ (- ◦ [id, 1])])
def fact = (/1 *) ◦ ι
Haskell: test elem [] = False
test elem (x:lst) | x == elem = True
| otherwise = test elem lst
FP: def test = null ◦ 2 → F; eq ◦ [1, hd ◦ 2] → T; test ◦ [1, tl ◦ 2]
def test = (/F or) ◦ (α eq) ◦ distl
Haskell: fact n = foldr (*) 1 [1..n]
Haskell: test elem = (foldr (||) False) . (map (== elem))
test : <5, <1,7,5,2>>
(/F or) : ((α eq) : (distl : <5, <1,7,5,2>>))
(/F or) : ((α eq) : <<5,1>,<5,7>,<5,5>,<5,2>>)
(/F or) :
T

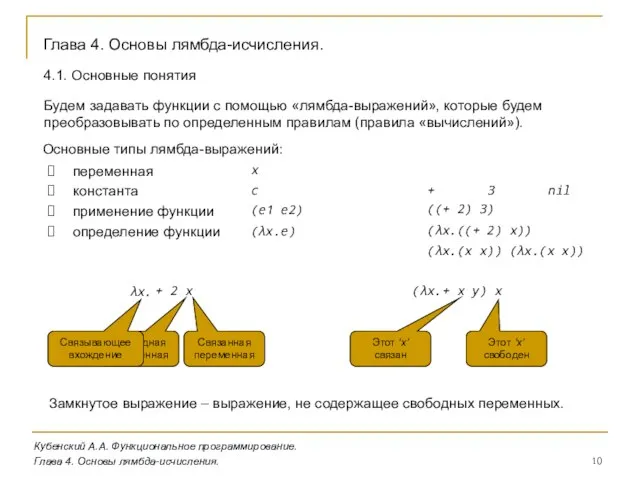
Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Глава 4. Основы лямбда-исчисления.
Будем задавать функции с помощью «лямбда-выражений», которые будем
преобразовывать по определенным правилам (правила «вычислений»).
Основные типы лямбда-выражений:
переменная
константа
применение функции
определение функции
x
+
3
nil
c
((+ 2) 3)
(e1 e2)
(λx.((+ 2) x))
(λx.e)
+ 2 x
λx.
Свободная переменная
Связывающее вхождение
(λx.+ x y) x
Связанная переменная
Этот ‘x’ связан
Этот ‘x’ свободен
4.1. Основные понятия
Замкнутое выражение – выражение, не содержащее свободных переменных.
(λx.(x x)) (λx.(x x))

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Правила преобразований выражений.
1. δ-редукция
f e1 e2... ek → result
+ 3 5 → 8
or T F → T
2. β-редукция
(λx.e1) e2 → e1{x|e2}
(λx.+ 1 x) 5 → + 1 5
(λx.x x)(λx.x x) → (λx.x x)(λx.x x)
3. α-преобразование
λx.e1 ↔ λz.e1{xсв.|z}
λx.((λy.λx.+ x y) x) →
λz.((λy.λx.+ x y) z)
4. η-преобразование
λx.E x ↔ E
λx.((λy.λx.+ x y) x) →
(λy.λx.+ x y)

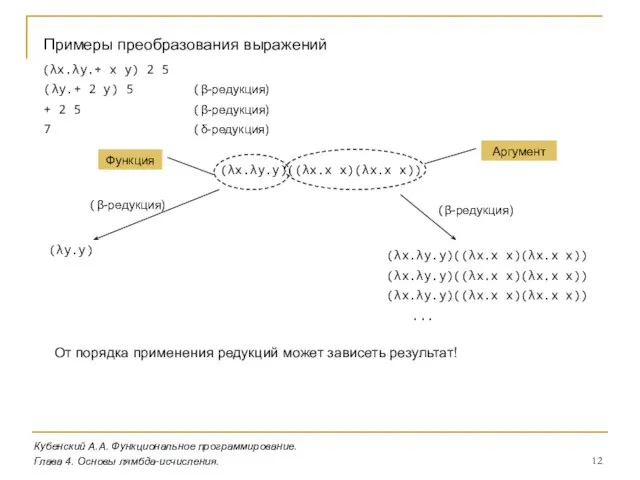
Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Примеры преобразования выражений
(λx.λy.+ x y) 2 5
(λy.+ 2 y) 5 (β-редукция)
+ 2 5 (β-редукция)
7 (δ-редукция)
(λx.λy.y)((λx.x x)(λx.x x))
Функция
Аргумент
(λy.y)
(β-редукция)
(β-редукция)
(λx.λy.y)((λx.x x)(λx.x x))
(λx.λy.y)((λx.x x)(λx.x x))
(λx.λy.y)((λx.x x)(λx.x x))
...
От порядка применения редукций может зависеть результат!

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Ромбическое свойство системы редукций
α0 → α1 → … → αk
α0 →* αk
Нормальная форма: лямбда-выражение, к которому не применимы β- и δ-редукции
α0
→
→
β1
β2
ω
→*
→*
Теорема (Черча – Россела): система преобразований, основанная на применении
β-редукций обладает ромбическим свойством.
Следствие: лямбда-выражение не может иметь более одной нормальной формы.
Замечание: в некоторых случаях применение редукций может, в зависимости от
порядка, либо приводить к нормальной форме, либо не приводить к ней.
существует (?) форма ω
Отношение →* это
рефлексивное транзитивное
замыкание отношения →

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Стандартные порядки редукций.
Редекс (redex) – выражение, к которому применима одна из редукций.
Reducible Expression – редуцируемое выражение.
β-редекс; δ-редекс…
Выражение может содержать (или не содержать) один или несколько редексов.
Выражение (λx.λy.y)((λx.x x)(λx.x x)) содержит два редекса.
Внутренний редекс
Внешний редекс
Самый левый (самый правый) редекс – текстуально расположен левее (правее) других.
Самый внутренний редекс – не содержит внутри себя других редексов.
Самый внешний редекс – не содержится внутри никакого другого редекса.
Аппликативный порядок редукций – редукция всегда применяется к самому левому из
самых внутренних редексов
Нормальный порядок редукций – редукция всегда применяется к самому левому из
самых внешних редексов

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Еще пример редукции выражения
(λx.* x x)((λy.+ 1 y) 2)
Аппликативный порядок редукций
(λx.* x x)(+ 1 2)
(λx.* x x) 3
* 3 3
9
– нормальная форма
Нормальный порядок редукций
* ((λy.+ 1 y) 2) ((λy.+ 1 y) 2)
* (+ 1 2) ((λy.+ 1 y) 2)
* 3 ((λy.+ 1 y) 2)
* 3 (+ 1 2)
* 3 3
9
– нормальная форма
β-редукция
β-редукция
δ-редукция
β-редукция
δ-редукция
β-редукция
δ-редукция
β-редукция
δ-редукция
δ-редукция

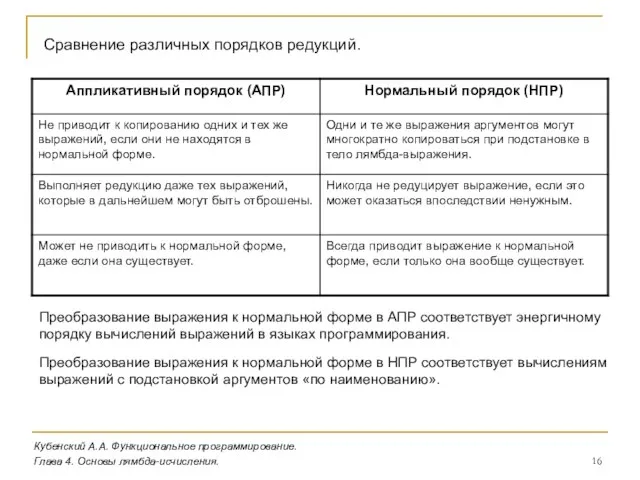
Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Сравнение различных порядков редукций.
Преобразование выражения к нормальной форме в АПР соответствует энергичному
порядку вычислений выражений в языках программирования.
Преобразование выражения к нормальной форме в НПР соответствует вычислениям
выражений с подстановкой аргументов «по наименованию».

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Проблема конфликта имен.
λx.((λy.λx.+ x y) x)
Свободное вхождение переменной
Связанное вхождение переменной
λx.(λx.+ x x)
λz.((λy.λx.+ x y) z)
α-преобразование
λz.(λx.+ x z)
η-преобразование
λy.(λx.+ x y)

Кубенский А.А. Функциональное программирование.
Глава 4. Основы лямбда-исчисления.
Слабая заголовочная нормальная форма (СЗНФ)
Выражение, не имеющее свободных переменных (замкнутое)
находится в СЗНФ, если оно имеет один из следующих видов:
Константа
c
Определение функции
λx.E
Частичное применение функции
P E1 E2 ... Ek
Выражение λx.((λy.λx.+ x y) x) находится в СЗНФ.
Вычисления, происходящие при исполнении программы в «ленивых» вычислениях,
соответствуют редукции выражения в НПР до приведения к СЗНФ, дополненной
эффектом «разделения» значений переменных при подстановке аргумента,
еще не находящегося в СЗНФ.
(λx.+ x x)(* 2 3)
+ (* 2 3) (* 2 3)
+ 6 (* 2 3)
+ 6 6
12
+ x x
(* 2 3)
+ x x
6
12