Горные машины и оборудование. Курс лекций

занных между собой по своим техническим параметрам так, что обеспечива-
ют рациональное производство всех работ этого процесса (Рис. 1.2 – 1.4).
По функциональному назначению горные машины и комбайны делятся
на:
- выемочные, - уборочные,
- проходческие, - штабелюющие,
- очистные, - погрузочные,
- экскавирующие, - транспортирующие,
- бурильные, - вспомагательные.
По положению в пространстве всей машины при выполнении рабочего
процесса различают:
- мобильные машины, т.е. выполняющие технологические операции в
одновременно с перемещением самой машины;
- стационарные, т.е. не меняющие своего положения в процессе экс-
плуатации относительно разрабатываемого месторождения полезных ископа-
емых;
- передвижные (полустационарные), выполняющие технологическую
операцию не передвигаясь, но относительно быстро меняющие местополо-
жение в транспортных режимах.
В свою очередь мобильные технологические машины подразделяют-
ся на:
- самоходные, т. е. машины с активным движителем, обеспечивающий
передвижение машины в рабочем и транспортном положениях;
- прицепные, имеющие пассивный движитель, обеспечивающим пере-
движение машины за счет мощности специальной машины - тягача;
- полуприцепные, оборудованные движителем, воспринимающим до
80% эксплуатационной массы машины и агрегатируемые с тягачом через
специальные устройства, передающие часть нагрузки, действующей на ма-
шину, на тягач;
- навесные, агрегатируемые на тракторах или универсальных шасси с
помощью специальных навесных устройств;
- полунавесные, представляющие собой оборудование, агрегатируемое
с тягачом и имеющие собственную опору (движитель).
История развития горных машин неразрывно связана с развитием всей
техники и, в первую очередь, с развитием энергетических средств: ручной
инструмент – тяговая сила животных – энергия пара – электрическая энергия
– двигатели внутреннего сгорания.
Добыча и использование полезных ископаемых человеком, чему есть
материальные свидетельства, известна с каменного века.
Промышленная добыча полезных ископаемых с использованием про-
стейших механизмов на основе применения мускульной энергии животных
началась только в ХVI-м веке. Несколько позднее для разрушения массивов
горных пород начали использовать порох, а потом и другие взрывчатые ве-
щества. Первым энергетическим средством в горном деле было водяное ко-
лесо, упоминания о котором датируются ХVII-м веком. Использование паро-

вых двигателей при добыче полезных ископаемых известно с ХVIII-го века.
В этот же период, и особенно, в ХIX-м веке, начинается широкое применение
механизированных средств труда: баровая врубовая машина – 1864 год, Ан-
глия; экскаватор с паровым двигателем – 1834 г., США; пневматический
перфоратор – 1860 г., Франция.
Применение таких технических средств позволило во много раз увели-
чить объёмы добычи горных пород. Ещё более существенно возросли эти
объёмы при появлении электрического привода, который начал использо-
ваться в горных машинах с 1880 г, Англия. Ещё большие возможности меха-
низации труда в горном производстве возросли с появлением двигателей
внутреннего сгорания, которые начали применяться особенно интенсивно в
приводах машин для выполнения открытых горных работ. В конце ХIX-го
века созданы первые комбайны для производства особенно трудоёмких про-
ходческих работ при подземных разработках месторождений полезных иско-
паемых -1897 г., Россия.
В настоящее время использование полезных ископаемых, как в количе-
ственном, так и в качественном разнообразии непрерывно увеличивается и
расширяется. Объёмы выемки горных пород в последний период удваива-
лись за последние 15-20 лет и достигли объёма более 100 млрд. тонн в год.
В настоящее время горная техника совершенствуется в направлении
использования технологий добычи с возможно меньшим участием людей
непосредственно в местах добычи. Это достигается как за счет совершен-
ствования конструкций горных машин и механизмов, так и, в значительной
степени, за счет применения новых систем управления, основанных на со-
временных электронных средствах.
В Беларуси горное машиностроение – сравнительно молодая отрасль
промышленности, хотя некоторые горные машины производятся достаточно
давно. Это особенно относится к машинам по добыче торфа, производство
которых было начато до второй мировой войны. В 1946 году на базе завода
торфяного машиностроения организовано предприятие по выпуску карьер-
ных самосвалов большой грузоподъемности (Белорусский автомобильный
завод «БелАЗ», г. Жодино). Производство технических средств для подзем-
ных горных разработок при добыче и переработке калийных руд (Старобин-
ское месторождение) начато в Солигорском институте проблем ресурсосбе-
режения с Опытным производством и в настоящее время развивается доста-
точно высокими темпами. Подготовка специалистов горно-добывающего
профиля, в том числе конструкторов, производителей горных машин, а также
специалистов по их эксплуатации организована в Белорусском национальном
техническом университете и его филиале в Солигорске.

Рисунок 1.2 – Уборочный машинно-тракторный агрегат
на технологической площадке разрабатываемого торфяного месторождения
Рисунок 1.3 - Погрузка фрезерного торфа
в вагоны железнодорожного состава узкой колеи

Рисунок 1.4 – Технологический комплекс машин
на карьере по добыче мела
Рисунок 1.5 – Проходческий комбайн с соосными роторами
в подземной горной выработке месторождения калийных солей

1. ОБЩАЯ СТРУКТУРА
И ОСНОВЫ УСТОЙЧИВОСТИ ГОРНЫХ МАШИН
1.1 Современная структура горных машин и требования к ним
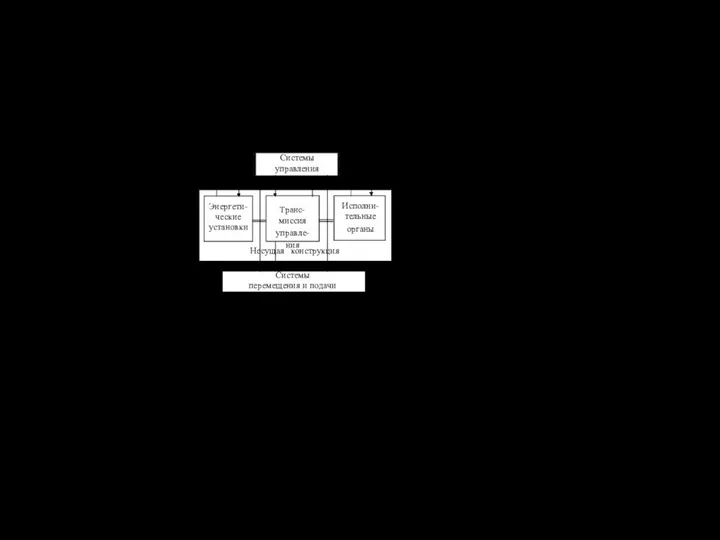
Большое многообразие горных машин затрудняет их отображение ка-
кой либо одной общей структурной, функциональной или расчетной схема-
ми. Тем не менее, в целях систематизации изложения будем рассматривать
горную машину как механическую систему, состоящую из следующих эле-
ментов, которые обозначены на рис.1.2.
Рисунок 1.2 – Структурная схема горной машины
Эта схема указывает на сложность горных машин, представляющих со-
бой большие и сложные по структуре системы. Вместе с тем, каждая часть
этой схемы также есть большая система и в этом смысле она может быть
изучена самостоятельно. Исполнительные органы и другие части машины
так или иначе взаимодействуют с горной породой, свойства которой в значи-
тельной степени определяют конструкцию и режимные параметры горных
машин.
Современные технологии горного производства, объёмы горных работ
и условия их выполнения, а также уровень развития техники, позволяют
сформулировать к таким машинам ряд требований, которые можно разделить
на общетехнические и специальные. Общие требования включают в себя
технические, экономические, социальные и экологические. Технические тре-
бования обычно вносятся в документацию, сопровождающую машину весь
её жизненный цикл, и отражают её технический уровень, надёжность и усло-
вия эксплуатации. Экономические требования объединяют сведения о цене,
уровне затрат при эксплуатации, ремонте и утилизации машины. Социальные
Системы
управления
Системы
перемещения и подачи
Транс-
миссия
управле-
ния
Исполни-
тельные
органы
Энергети-
ческие
установки
Несущая конструкция

требования включают санитарно-гигиенические условия работы персонала,
его безопасность, комфортность труда, лёгкость и удобство управления. Эко-
логические требования выражаются мероприятиями, обеспечивающими за-
щиту окружающей среды от вредных воздействий, возникающих при работе
машин. В последнее время, в связи с общим повышением требований к гор-
ным машинам, в зависимости от конкретных условий эксплуатации предъяв-
ляются ряд специальных требований, ужесточающих их производство и экс-
плуатацию - взрыво- и пожаробезопасность, проходимость, маневренность,
габаритные размеры, обеспечивающие перемещения в ограниченном про-
странстве горных выработок.
1.2 Основные свойства горных пород и их исчисление
Среди комплекса физических свойств горных пород наибольшее влия-
ние на условия работы горных машин оказывают их механические характе-
ристики. Эти характеристики обычно делят на группы размерно-
плотностных, прочностных, упруго-пластичных, реологических и других
свойств. Среди размерно-плотностных свойств наибольшее значение имеют
плотность и фракционный состав природной или измельченной тем или
иным способом породы. Плотность горных пород изменяется в довольно
значительных пределах и зависит от физического состояния породы (содер-
жания влаги, пористости, фракционного состава и др.) Фракционный состав
горных пород в естественном состоянии, а также подвергнутых разрушению
горнодобывающими и горно-перерабаты-вающими машинами, оценивается с
помощью относительных выходов частиц породы определённых размеров.
Эти выходы определяются посредством применения различных законов рас-
пределения частиц по их размерам.
Среди прочностных свойств горных пород наиболее часто используют-
ся их пределы прочности при сжатии, изгибе и сдвиге. Наиболее общей ха-
рактеристикой прочностных свойств считается коэффициент крепости и
шкала прочности М. М. Протодьяконова. Эта шкала построена на определе-
нии коэффициента крепости путем деления временного сопротивления сжа-
тию породы на 10, то есть коэффициент крепости определяется соотношени-
ем
10
f=σсж, (1)
где сопротивление сжатию σсж определяется в МПа.
От коэффициента крепости горных пород зависят затраты на разруше-
ние массива породы в залежи, особенно механическим способом разрушения.
Шкала проф. Протодьяконова до настоящего времени является основой
оценки прочностных характеристик большинства горных пород. Она приво-
дится в таблице 1.1.

Таблица 1.1 – Категории горных пород в зависимости от коэффициента кре-
пости
Категория Степень крепости Примеры пород Коэффициент
крепости
1 Породы высшей крепости Базальты,
кварциты
20 и более
2 Очень крепкие Крепкие граниты 15
3 Крепкие породы Граниты, мрамор,
очень крепкие
известняки
10 - 8
4 Достаточно крепкие Обыкновенные песча-
ники, железные руды,
сланцы
6 – 5
5 Породы средней крепости Глинистые
сланцы, мергель,
5 - 4
6 Довольно мягкие породы Мягкие сланцы,
мел, крепкие угли,
калийные соли,
каменистый грунт
4 – 3
7 Мягкие породы Глина, мягкий уголь,
гравий
1 – 0,8
8 Землистые породы Растительный грунт,
торф, суглинок
0,6
9 Сыпучие породы Песок,
мягкий гравий,
насыпной грунт
0,5
10 Плывущие породы Плывуны, сапропель в
водоемах, другие
разжиженные породы
0,3
Вместе с коэффициентом крепости проф. Протодьяконова для опреде-
ления прочностных свойств горных пород используют пределы прочности
при сжатии, растяжении и изгибе. Упругие свойства горных пород чаще все-
го характеризуются модулем Юнга и коэффициентом Пуассона. Хотя в клас-
сическом для материаловедения виде эти характеристики определяются за-
труднительно, тем не менее, в исследованиях и расчетах горных машин они
используются очень часто и понимаются как величины, дающиеся классиче-
скими определениями
ε
σ
E= ;
ε
ε
μ= ′, (1.2)
где E - модуль Юнга (модуль упругости), Па;
σ - напряжение растяжения (сжатия) образца породы, Па;
ε = dl/l - относительная продольная деформация;
l - длина испытуемого образца, м;
dl - удлинение образца, м;
ε′=dl′l′ - относительная поперечная деформация;
l′ и dl′- поперечный размер образца и его изменение, м;

μ - коэффициент Пуассона.
Помимо модуля упругости часто используется такая характеристика
горных пород, как модуль G сдвига, который определяется выражением
ε
τ
G= , (1.3)
где τ - касательное напряжение при сдвиге;
ε - угол сдвига.
Модули E деформации и сдвига при соблюдении закона Гука связаны соот-
ношением
=2(1+μ)
E
G . (1.4)
Кроме перечисленных характеристик физических свойств горных по-
род используются и ряд других характеристик, отражающих взаимодействие
горных машин с породами. Среди них наиболее часто встречаются: твер-
дость, контактная прочность, угол естественного откоса, разрыхленность,
пористость, трещиноватость, абразивность, вязкость и некоторые другие.
Для оценки взаимодействия режущих элементов механических органов
разрушения с породой используются их такие характеристики, как сопротив-
ляемость резанию и удельное сопротивление резанию. Большинство пере-
численных свойств пород определяются опытным путем с использованием
специальных приборов и технических устройств. Особое значение среди этих
характеристик имеют сопротивляемость и удельное сопротивление разруше-
нию или резанию, о чем подробнее будет изложено в разделе 2.
1.3 Пространственная ориентация горной машины
Большинство горных машин выполняя операции по выемке, транспор-
тированию и переработке полезных ископаемых тем или иным образом пе-
ремещаются в пространстве. Эти перемещения могут быть как непрерывны-
ми, так и периодическими. В любом случае для определения движения ма-
шин в целом и отдельных ее механизмов и частей необходимо выбрать си-
стемы координат, в которых это движение определяется.
Неподвижная система координат обычно связывается с географиче-
ским положением месторождения полезного ископаемого. Подвижная систе-
ма координат передвигается вместе с машиной и ее полюс совмещается с ка-
кой-либо характерной точкой машины (центр масс, центр опорной площади и
т. д.). Положение подвижной системы координат относительно неподвижной
обычно задается декартовыми координатами её полюса и тремя углами Эй-
лера, с помощью которых определяется сферическое движение подвижной
системы.
При использовании углов Эйлера положение подвижной системы

обычно определяют таблицей косинусов между осями подвижной и непо-
движной систем декартовых координат. Углы Эйлера введем подобно кора-
бельным и самолетным осям [1] таким образом (рис.1.2), что перевод непо-
движной системы OXYZ в положение подвижной системы осуществляется
углами рысканья, поперечного и продольного крена.
Таблицу косинусов между подвижными и неподвижными осями вы-
числим как произведение трех матриц направляющих косинусов, образу-
ющихся после каждого из перечисленных поворотов. Обозначив эти мат-
Z
n
к
0 0 1
sin cos 0
cos sin 0
a
X YZ
ψ ψ
ψ ψ
ψ=− . (1.3)
Рис. 1.3 - Ориентация подвижных осей
Элементы этой матрицы (рис. 1.3) равны косинусам углов между соот-
x
y
z
Z
Y
X
п
m
к
ψ θ
θ
φ
ψ
φ

Аналогично
m
n
x
sin 0cos
0 1 0
cos0 sin
a
к n Z
θ θ
θ θ
θ
−
= ; (1.4)
z
y
x
0 sin cos
0cos sin
1 0 0
a
x nm
ϕ ϕ
ϕ ϕ ϕ
−
= . (1.5)
Тогда матрица направляющих косинусов определится как произведе-
ние трех приведенных матриц [1]
Произведя умножение, найдем
z
y
x
cossincos sinsin cossinsin sincos coscos
cossinsin cossin sinsinsin coscos sincos
coscos cossin sin
A
X Y Z
ϕθψ ϕψ ϕθψ ϕψ ϕθ
ϕϕθ ϕψ ψϕθ ϕψ ϕθ
θψ θψ θ
+ −
− +
⋅ ⋅ −
= (1.7)
Машина в некоторых случаях рассматривается в состоянии покоя, по-
дим к следующему виду таблицы направляющих косинусов:
z
y
x
cossin sin coscos
sinsin cos sincos
cos 0 sin
A
X Y Z
ϕθ ϕ ϕθ
ϕθ ϕ ϕθ
θ θ
−
−
= . (1.8)
Наконец, машина может находиться в положении, когда имеет место
только продольный крен, т.е. угол θ - поперечного крена равен нулю. В этом
случае матрица направляющих косинусов имеет еще более простой вид
z
y
x
0 sin cos
0cos sin
1 0 0
A
X Y Z
ϕ ϕ
ϕ ϕ
−
= . (1.9)
Зная направление действия сил в одной из систем, можно при помощи

(1.8) и (1.9) найти проекции сил на оси другой системы.
Возможны и другие варианты таблицы направляющих косинусов, ко-
торые соответствуют различным ситуациям, возникающим в практике функ-
ционирования горных машин.
1.4 Положение центров масс
и давления машин на опорное основание
При определении координат центра масс в инженерных расчётах гор-
ная машина рассматривается как механическая система, состоящая из мате-
риальных частей, координаты центров масс которых известны. Как и для
большинства технологических машин, совершающих какие-либо перемеще-
ния в пространстве, для большинства горных машин важнейшей характери-
стикой оценки их устойчивости является положение центра масс. Радиус-
вектор центра масс в какой-либо системе координат, связанной с машиной,
определяется в общем виде интегралом
= ∫∫∫ ⋅⋅
V
rcm1ρrdV, (1.10)
где интегрирование производится по общему объёму V машины;
ρ - плотность материала машины, в общем случае зависящая от x, y, z;
r=x2+y2+z2 - радиус материальной точки с плотностью ρ;
m - общая масса машины.
Тогда координаты центра масс машины
∑
∑ ⋅
=
n
i
n
i i
c
m
mx
x
1
1 ;
∑
∑ ⋅
=
n
i
n
i i
c
m
my
y
1
1 ;
∑
∑ ⋅
=
n
i
n
i i
c
m
mz
z
1
1 , (1.11)
где mi - масса отдельной материальной части;
xi, yi, zi - координаты ее центра масс в подвижной системе отсчета;
n - количество материальных частей.
При работе или простом перемещении горной машины на нее кроме
сил тяжести действуют силы взаимодействия исполнительных органов с по-
родой и другие внешние нагрузки. Эти нагрузки тем или иным способом че-
рез механизм перемещения (ходовое устройство) передаются на опорное ос-
нование. Взаимодействие ходового устройства с опорным основанием харак-
теризуется рядом параметров, среди которых одним из важнейших является
давление ходового устройства на опорное основание.
Различают несколько характеристик распределения давления по опор-
ному основанию: среднее, максимальное и минимальное давление, положе-
ние центра давления и ядра сечения. Определим эти характеристики.
Центром давления машины на грунт называется точка, радиус-вектор

которой определяется выражением
∫∫
∫∫
⋅
⋅ ⋅
∂=
S
S
pds
rpds
Иначе, центр давления представляет собой точку приложения равно-
действующей сил давления машины на несущее основание. Из последнего
определения следует, что эта точка лежит в опорной плоскости ходового
устройства.
Записав (1.12) в проекциях на оси подвижной системы координат, по-
лучим:
∫∫
∫∫
∫∫
∫∫
⋅
⋅ ⋅
=
⋅
⋅ ⋅
∂= ∂
S
S
S
S
pds
ypds
;y
pds
xpds
Интегралы в числителе выражений (1.13) представляют собой (рис. 1.4)
x
S
y
S
С другой стороны
Mx=Mx(F);My=My(F),
чая силы реакций грунта на ходовое устройство).
геометрическую сумму силы тяжести, приложенной в центре масс, сил реак-
ций разрабатываемой породы на рабочие органы, крюкового усилия и т. п.
Тогда на основании теоремы о моменте равнодействующей имеем
() ( ) ()
M(F)M(mg)M(P).
MFMmgMP;
y y y
x x x
= +
= +
(1.14)
m – масса машины;
мальных реакций опорной поверхности).

Интеграл, стоящий в знаменателе выражений (1.13), есть общая сила
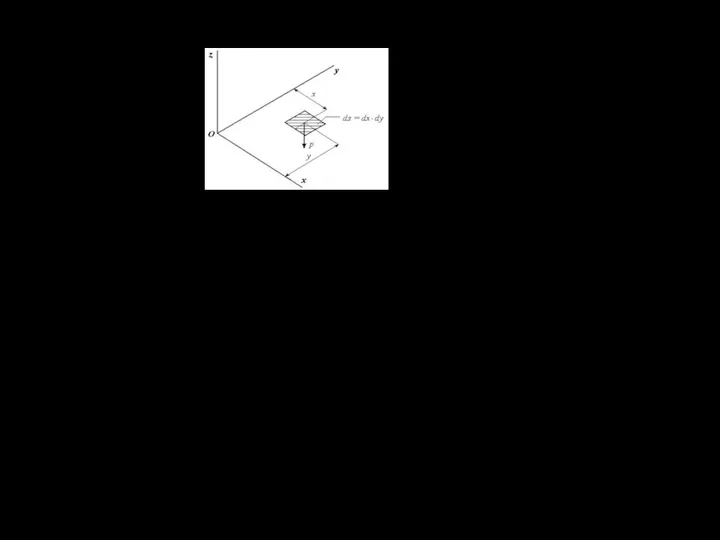
давления машины на несущее основание
z
S
нормально к опорной поверхности. Эта равнодействующая, есть сумма про-
екций силы тяжести и равнодействующей внешних сил на ось Oz
внешних сил на ту же ось.
С учетом этого, окончательно
z
x
z
y
F
M
;y
F
M
органа с машиной. Если рабочий орган закреплен на машине жестко, то
зываемым неровностью рельефа поверхности или различной деформацией

системе осей Oxyz, связанной с машиной. В ряде машин, предназначенных
для рытья осушительных каналов или планирования поверхности, с целью
создания постоянного наклона дна каналов и требуемого профиля поверхно-
сти рабочие органы независимо от положения самой машины сохраняют за-
данное положение относительно неподвижной (инерциальной) системы осей
Если центр давления не совпадает с центром опорной поверхности, то
давление машины на грунт распределено неравномерно. Это может привести
к тому, что даже при допустимом значении среднего давления машина поте-
ряет устойчивость из-за больших деформаций опорного основания в местах с
большими местными давлениями. Поэтому кроме среднего давления вычис-
ляются его наибольшее и наименьшее значения. При этом считают, что де-
формации несущего основания пропорциональны давлениям, т.е. напряжен-
ное состояние грунта подчиняется закону Гука. В этом случае при вычисле-
нии среднего и экстремальных значений пользуются формулами:
S
F
p= z, (1.17)
где p – среднее давление;
S – площадь опорной поверхности.
,
;
min
max
y
y
x
x
y
y
x
x
W
M
W
M
p p
W
M
W
M
p p
=− −
=+ +
(1.18)
же осей.
Расчетные значения давлений сравнивают с допустимыми [р] значени-
ями давления, которые зависят от типа ходового устройства и свойств опор-
ного основания и выбираются по нормативным документам или определяют-
ся в зависимости от прочности опорного основания и типа, размеров и фор-
мы ходового устройства. В большинстве случаев с достаточной для практики
точностью можно пользоваться справочными и нормативными данными.
Помимо величин среднего и экстремальных значений давления весьма
важной характеристикой статической устойчивости горных машин является
положение центра давления относительно ядра сечения. Напомним, что, как
и в сопротивлении материалов, ядром сечения опорной площади ходового
устройства (рис.1.5) горной машины называется часть ее опорной поверхно-
сти при расположении внутри которой центра давления минимальное значе-
ние давления положительно, т. е. удовлетворяет условию pmin0.

Рисунок 1.5 – К определению допустимого положения центра давления:
Д - допустимое положение центра давления; Д’ - недопустимое;
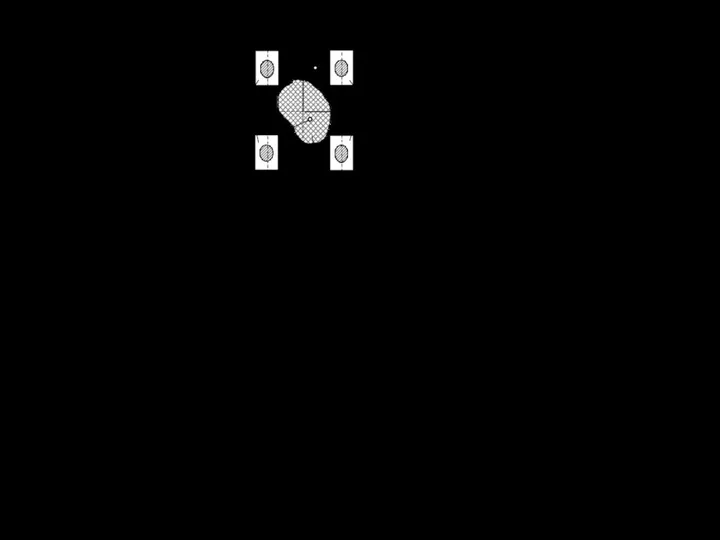
1 – ядро сечения; 2 – опорная площадь ходового устройства
Координаты центра давления вычисляются по формулам (1.16), а фор-
ма и размеры ядра сечения из условия pmin=0, или
y
y
x
x
W
M
W
M
0=p− − , (1.19)
которое указывает на то, что использованные условия требуют вычисления
Wx, Wy для каждой конструкции ходового устройства (гусеничные, колес-
ные, шагающие и т. п.) [2, 3, 4].
Кроме оценки устойчивости горной машины по давлению на опорное
основание и положению центра давления ее оценивают с помощью верти-
кального положения центра масс и допустимых значений продольного и по-
перечного углов крена машины. При этом определяются допустимые по
опрокидыванию вокруг крайних в продольном и поперечном направлениях
точек опорной площади ходового устройства значения опрокидывающих
моментов. Такие расчеты дают возможность оценить статическую устойчи-
вость машины, но не оценивают ее динамическую устойчивость, которая ис-
следуется специальными способами [5]. Для массивных и крупногабаритных
горных машин, положение центра масс относительно опорной поверхности
имеет особо большое значение вследствие больших атмосферных нагрузок
(ветер, дождь, гололёд, снег), периодических круговых движений верхних
поворотных частей, а также отклонений опорных поверхностей от горизонта.
Поэтому для таких машин регламентируется, как правило, допустимый угол
наклона опорной поверхности и её прочностные свойства. Высота центра
масс таких машин также очень существенно влияет на их устойчивость. Пре-
дельно допустимая высота центра масс (рис. 1.6) горной машины может быть
определена из уже упоминавшегося условия pmin≥0. Если машина располо-
1
2 2
Д'
Д
x
y

жена на опорной поверхности, наклоненной под углом φ к горизонту и
нагружена внешними силами, равнодействующая которых Р. кроме того,
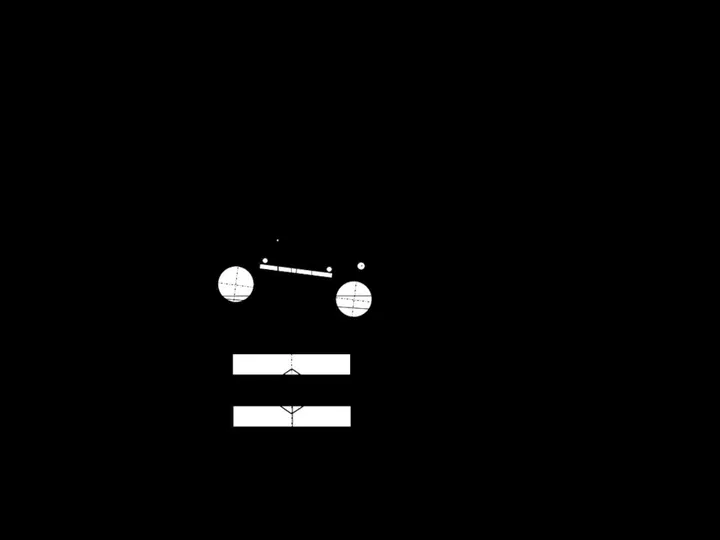
определены максимальные и минимальные деформации крайних точек её
опорной поверхности, момент внешних нагрузок относительно осей Ох и Оу,
а также моменты сопротивления опорной площади ходового устройства от-
носительно осей Ох и Оу, то условие равенства нулю минимального давления
даёт уравнение
( ) ()
x
z c x
W
mgymg MP
S
0=F− ⋅ ⋅+ ⋅ ⋅sinϕ+γ+
, (1.20)
где
a
h h
γ=arctgmax−min - угол крена, возникающий из-за неравномерности
давления.
Рисунок 1.6 – К определению высоты центра масс
по условию продольной устойчивости
(φ+γ)
hmin
hmax
φ
γ
m·g zc
z
y
x
O
a

Рис. 1.6,б – Крен шагающего экскаватора на откосе мелового карьера
в период весенней распутицы

Из этого соотношения может быть найдено максимальное положение
центра масс
()
⋅ ⋅ ⋅ (ϕ+γ)
⋅− ⋅ ⋅ ⋅− ⋅
Smgsin
FWSmgySMP
zc z x c x . (1.21)
Последнее ограничение на вертикальное расположение центра тяжести
получено из условия расположения центра давления в пределах ядра сечения.
Это условие является довольно жестким и допускает кратковременную рабо-
ту машины без угрозы её опрокидывания. Однако длительной работы маши-
ны с постоянным или периодическим выходом центра давления за пределы
ядра сечения, конечно, не допускается. Это утверждение относится и к попе-
речной устойчивости машин.
Для определения максимального положения центра масс по условию
поперечной устойчивости рассмотрим, как и выше, положение центра давле-
ния машины в зависимости от её поперечного крена и величины внешних
нагрузок (рис. 1.7). В худшем, с точки зрения поперечной устойчивости, по-
ложении машины условие отрыва части ходового устройства от опорной по-
верхности
0
x
z y
W
M
S
F− , (1.22)
где My=m⋅g⋅sin(θ+β)⋅zc−m⋅g⋅cos(θ+β)⋅xc−My(P);
B
h h
β=arctgmax−min - угол поперечного крена вследствие неравномерности
деформаций несущей поверхности.
Рисунок 1.7 – Определение положения центра масс
из условия допустимых значений поперечного крена
Р
(θ+β)
z
hmax
hmin b
m·g·sin(θ+β)
Z
X
β x

Подставив в (1.22) значение Му и разрешив его относительно zc, имеем
( ) ()
(αβ)
θβ
⋅ ⋅ ⋅ +
⋅ ⋅ ⋅ +− ⋅ − ⋅
cos
sin
Smg
Smg SMPFW
zc y z x. (1.23)
Из значений zc, определённых по формулам (1.21) и (1.23), выбирается,
естественно, меньшее значение. При этом необходимо учитывать то обстоя-
тельство, что условия (1.21) и (1.23) дают значения zc, при которых использу-
ется вся опорная поверхность машины и не выполнение этих условий не
означает, что машина опрокидывается. Вследствие этого небольшие по вре-
мени периоды работы некоторых машин, например, бульдозеров, иногда до-
пускаются. Однако в целом, надёжная эксплуатация горных машин на него-
ризонтальных деформируемых несущих основаниях обеспечивается при рас-
положении центров масс на высоте, определяемой обсуждаемыми формула-
ми.

2. ОСНОВЫ ТЕОРИИ РАЗРУШЕНИЯ ГОРНЫХ ПОРОД
ИСПОЛНИТЕЛЬНЫМИ ОРГАНАМИ
2.1 Способы разрушения горных пород
Первичное взаимодействие горной машины с массивом породы заклю-
чается в его разрушении и выемке отбитой горной массы. В зависимости от
физико-механических свойств массива процесс разрушения и выемки может
быть осуществлен несколькими способами, основные из которых следую-
щие:
- механический;
- гидромеханический;
- взрывной;
- смешанные;
- специальный.
При механическом способе разрушение производится непосредствен-
ным воздействием инструмента на породу (удар, резание, скалывание и т. п.).
особенность заключается в том, что инструмент должен быть прочнее поро-
ды. Гидромеханический или просто гидравлический способ разрушения реа-
лизуется воздействием на породу струи или потока жидкости высокого дав-
ления.
Взрывной способ разрушения массива горной породы основан на ее
разрушении давлением газов, образующихся в результате мгновенного горе-
ния взрывчатых веществ. Эффективность способов разрушения оценивается,
прежде всего, по их энергоемкости. Она зависит как от физико-механических
характеристик свойств горных пород, так и способа разрушения, а также ка-
чества используемого оборудования. Для механического разрушения удель-
ная энергоемкость колеблется в пределах 0,7 – 6,1 МДж/м3, для гидравличе-
ского 1,4 – 14,4 МДж/м3, взрывного 14,4 – 36 МДж/м3.
2.2 Взаимодействие разрушающих элементов с массивом породы
Механический способ разрушения породы чаще всего реализуется
двумя основными воздействиями – резанием и ударом, а также их различны-
ми сочетаниями. При выемке породы с её разрушением посредством резания
основными элементами породоразрушающего инструмента являются резцы
или зубки. Под зубками понимаются резцы с бесконечно тонкой режущей
кромкой (игольчатый резец).
Обычно резцами снабжаются большинство исполнительных органов
машин, разрушающих горные породы резанием. Это относится как к маши-
нам для разрушения пород с повышенной прочностью (различные землерой-
ные экскаваторы), так и к машинам, разрабатывающим породы с самыми вы-
сокими показателями крепости.
Характер взаимодействия резца с породой может быть весьма разнооб-
разным и зависит от кинематики движения, геометрии резца, свойств поро-

ды, материала резца и т. п. для наиболее часто применяемых резцов с линей-
ной режущей кромкой выделяются несколько типичных условий резания, в
зависимости от которых различают свободные, полусвободные, полублоки-
рованные, блокированные и щелевые резы, схемы которых приведены на
рис. 2.1.
Рисунок 23. Форма сечения стружки при различных видах резов:
а - полусвободный; б - полублокированный; в - блокированный (с выровненной поверхности); г -
угловой; д - щелевой (h - глубина резания; t - шаг резания; b - ширина резца; S - площадь сечения среза; (р -
угол развала бородки резца)
Рисунок 2.1 – Типовые схемы резов:
а – свободный; б – полусвободный; в – полублокированный;
г - блокированный; д - щелевой
В зависимости от характера взаимодействия резца с массивом породы
на него со стороны породы действуют силы, проекции равнодействующей
которых обозначим через Rx, Ry, Rz (рис.2.1). Ось Оу направим по касатель-
ной к траектории резца, Ох и Оz - перпендикулярно оси Оу так, как показано
на схеме. Сила Ry называется силой сопротивления резанию, а равная ей сила
Рр , приложенная со стороны резца – силой резания. Реакция горной породы
Rz, выталкивающая резец, называется силой сопротивления подаче, и сила Рz,
действующая на породу со стороны резца называется силой подачи. Кроме
сил Ry и Rz на него могут действовать и боковые силы Rx, особенно в усло-
виях глубоких подземных выработок.
Изучение взаимодействия режущих элементов с горными породами по-
священы труды профессора Санкт-Петербургского горного института Ивана
Августовича Тиме, который впервые предложил зависимость для определе-
ния силы резания,
Pp=ep⋅b⋅h, (2.1)
где ep – удельная работа резания;
b, h – ширина и толщина снимаемой резцом стружки.
Он первым обратил внимание и на то, что ширина и толщина стружки
оказывает на величину силы резания разное влияние. Экспериментально этот
факт был подтверждён в работах К. А. Зворыкина, который предложил зави-
симость для определения удельной работы резания древесины
а) б) в) г) д)

h0,33
e
ep p
′
= . (2.2)
Эта формула является обобщённой формул Зворыкина К.И. и Солода
В.И., на которые мы уже ссылались.
Рисунок 2.2 – Схема взаимодействия резца с породой:
α - угол резания; γ - задний угол; β - угол заострения
Конструкции резцов, которые устанавливаются на исполнительных ор-
ганах горных машин весьма разнообразны и в основном зависят от условий
их работы. Чаще всего различают следующие основные типы резцов
(рис.2.3): радиальные; тангенциальные; радиально-торцовые.
Рисунок 2.3 – Основные типы резцов:
а – радиальный; б - тангенциальный; в - радиально-торцевой
Резцы являются первым элементом горных машин, разрушающим мас-
сив горной породы. Нагрузки, действующие на резцы так или иначе переда-
ются на последующие части машины. Поэтому определение этих нагрузок
является важнейшей задачей расчетов горных машин. Существуют различ-
ные способы и теории, объясняющие те или иные эффекты, возникающие
при разрушении массива горной породы резцами. При этом чаще всего уси-
лия подачи принимаются пропорциональными силам резания. Величина си-
лы резания зависит от большого числа факторов, включающих свойства по-
роды, резца и характер их взаимодействия, и в силу этого является случайной
даже при постоянных значениях этих факторов. Важнейшими её характери-
Rx Rx
Rz
P
R
Rz
Ry
β
α
γ
z
y x
z
а б в

стиками являются математическое ожидание и среднеквадратическое откло-
нение, которое определяется статистической обработкой экспериментальных
и опытных данных.
Если резец снимает слой породы постоянной толщины и стружка отби-
вается кусками, то схема изменения силы резания во времени может выгля-
деть так, как показано на рис.2.4.
Рисунок 2.4 – К определению характера силы резания:
tц – время, за которое резец проходит расстояние,
равное длине отбиваемых кусков породы.
Большинство исполнительных органов горных машин взаимодейству-
ют с породой так, что толщина снимаемой резцами стружки (глубина реза-
ния) является величиной переменной, что влечет за собой ещё большую не-
равномерность силы сопротивления резанию. Это обстоятельство не позво-
ляет установить функциональную зависимость между силой резания и фак-
торами, влияющими на неё. Среди этих факторов влияние на величину сил,
действующих на резец, оказывают геометрические характеристики резца,
шаг установки резцов, скорость резания и другие.
Однако, среди всех факторов, определяющих значение силы резания,
наибольшее значение имеет толщина снимаемой резцом стружки (глубина
резания). Поэтому в большинстве случаев предлагается показательная зави-
симость для вычисления силы резания (точнее сказать, её математического
ожидания) [2, 6]
n
Pp=k⋅h, (2.3)
где k и n - коэффициенты, учитывающие влияние всех основных факторов.
При резании грунтов часто используется формула
Pp=ep⋅h⋅b, (2.4)
где ep – удельное сопротивление резанию;
b – ширина стружки, снимаемой резцами.
P
tц t

Если сравнить формулы (2.3) и (2.4) и положить, что удельное сопро-
тивление резанию изменяется в зависимости от глубины резания также по
показательной зависимости, то эти формулы можно представить в виде:
Pp=ep⋅F=с1⋅hс2⋅F, (2.5)
где с1 и с2 - коэффициенты, имеющие тот же смысл, что и коэффициенты k и
n в формуле (2.3), причем
b
k
с1= ; с2=n−1. (2.6)
Для физического понимания смысла коэффициентов с1 и с2 проф. Кис-
лов Н.В. в [7] предлагает использовать зависимость для определения удель-
ного сопротивления резанию в виде
2
1
1
с
p h
h
e с ⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
= , (2.7)
где h1 = 1 м – условная толщина стружки.
Тогда с1 имеет размерность удельного сопротивления резанию и равен
ему при hh1=1, т. е. при h1 = 1 м.
Несмотря на практическое удобство использования формулы (2.7) и
возможность оценивать различные виды влияния h на удельное сопротивле-
ние резанию (рис.2.5) её применение ограничивается недостаточным наличи-
ем справочных данных для выбора значений коэффициентов с1 и с2.
Рисунок 2.5 – Влияние толщины стружки
на удельные затраты мощности
Вместе с тем, величина удельного сопротивления характеризует не
только саму силу резания, но и удельные затраты мощности, а также удель-
ные затраты энергии на разрушение породы резанием.
Действительно, если правую и левую части (2.5) умножить на диффе-
ренциал пути dS, проходимого резцом, то имеем
ep C2 > 1
h
C2 = 1
C2 < 1
C2 < 0

Pp⋅dS=ep⋅F⋅dS, (2.8)
или
dE=ep⋅dV,
тогда
dV
dE
ep= , (2.9)
где Е – энергия, затрачиваемая на разрушение массива резанием;
V – объём разрушаемой породы.
Таким образом, удельное сопротивление резанию численно равно
удельным затратам энергии на разрушение некоторого объёма массива гор-
ной породы. Если теперь левую и правую части (2.9) разделить на дифферен-
циал времени dt, то получим
Q
N
dVdt
dEdt
ep= =
/
/ , (2.10)
где N – мощность, затрачиваемая на разрушение массива резанием;
Q – объёмная производительность.
Это соотношение позволяет использовать значение удельного сопро-
тивления резанию, как удельных затрат мощности на разрушение массива ре-
занием и применять его в различного рода энергетических расчётах горных
машин. Для реального использования формулы (2.4) предлагается её вариант
в виде
22
11
KC
epKCh
= ⋅ ⋅ ⋅ , (2.11)
где К1 и К2 – коэффициенты, учитывающие соответственно отличие реаль-
ных прочностных свойств горной породы и условий резания от эталонных,
под которыми понимаются условия, в которых определены коэффициенты С1
и С2.
Помимо удельного сопротивления резанию в качестве характеристики
взаимодействия резцов с горными породами часто используется величина
сопротивляемости пород резанию, для определения которой созданы специ-
альные установки и методики [7].
На основании среднего значения сопротивляемости резанию согласно
ОСТ 12.47.001-73 «Комбайны очистные. Выбор параметров и расчёт сил ре-
зания и подачи на исполнительных органах. Методика» сила сопротивления
резанию углей определяется по формуле
( ϕ) cosβ
0,3 0,003 1
p cp хрcpcp з yф c от
сp
p
h tKKKKK
bhtgK
h
PA ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
+
+
= , (2.12)
где A - средняя сопротивляемость резанию, кН/м;

lp - ширина рабочей кромки резца, м;
hcp, tcp - средняя толщина (глубина) и ширина (шаг резания) стружки в
установившемся режиме, м;
ϕ - угол развала бороздки, градус;
Kxp - коэффициент, учитывающий хрупко-пластические свойства угля;
Kз - коэффициент обнажения забоя;
Kу - коэффициент, учитывающий влияние угла резания;
Kф - коэффициент влияния формы передней грани резца;
Kс - коэффициент учёта влияния схемы резания;
Kот - коэффициент, учитывающий влияние отжима угля в зоне работы
исполнительного органа.
К сожалению, формула (2.12), как и другие зависимости, полученные
на основе обработки экспериментальных данных, справедливы в своём
большинстве лишь для конкретных условий, в которых эти данные получе-
ны. В угольной промышленности созданы специальные установки для опре-
деления средней сопротивляемости резанию. Для этих целей используется
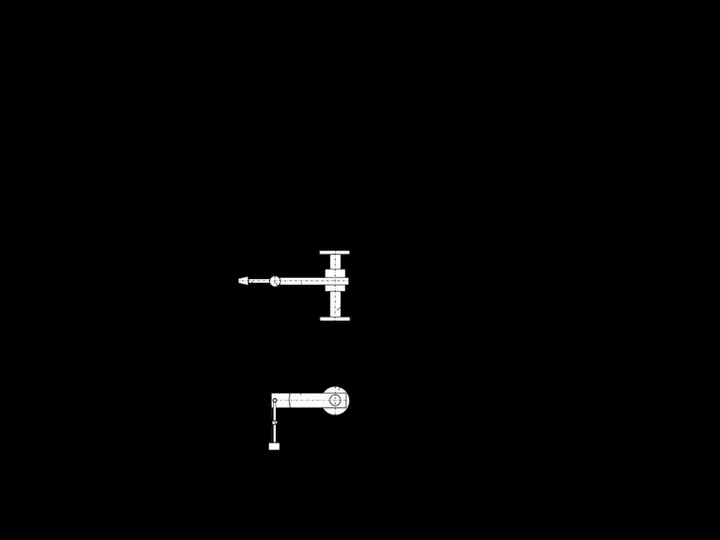
установка ДКС-2 (Рис. 2.6), а также динамометрические свёрла.
Рисунок 2.6 – Принципиальная схема установки ДКС-2:
1 – распорная стойка; 2 – держатель резца;
3 – резец; 4 – измерительное устройство
3 4 2 1
3 2 1
4

2.3 Геометрические и кинематические характеристики
взаимодействия режущих элементов горных машин с породой
В горных машинах для механического разрушения горных пород ис-
пользуются самые различные исполнительные органы: шнек-фрезы, диско-
вые и цилиндрические фрезы, шарошки, режущие коронки, соосные буры и
т. д. При этом режущие кромки их элементов разрушения совершают самые
разнообразные по виду траектории и скоростям резания движения. Эти дви-
жения можно разделить на две большие группы:
- обеспечивающие снятие (отделение) слоя массива горной породы с
постоянной толщиной стружки (постоянной глубиной резания);
- отделение слоя массива горной породы с переменной толщиной
стружки.
К первой группе машин относятся врубовые машины с рабочим орга-
ном в виде цепного бара, щеленарезные машины, экскаваторы непрерывного
действия с рабочим органом типа ковшовой рамы продольного или попереч-
ного копания. Вторую группу представляют проходческие комбайны плане-
тарно-дискового типа, очистные комбайны с рабочим органом типа «режу-
щий шнек», экскаваторы непрерывного действия с ковшовым ротором и дру-
гие машины, в которых резцы в процессе взаимодействия с массивом снима-
ют стружку непрерывно изменяющейся толщины. Толщина стружки зависит
от геометрии и кинематики пространственного движения режущих кромок
резцов. Эти движения можно разделить на движения с прямолинейными и
криволинейными траекториями, а также с постоянными и непостоянными
скоростями. Как правило, горные машины основную часть рабочего времени
работают с постоянными скоростями движения рабочих органов или со ско-
ростями, изменяющимися по известным законам (например, скорость движе-
ния поворотной платформы экскаватора). В этом смысле движение резцов
чаще всего сложное и может включать несколько независимых простых дви-
жений, как это отражено в таблице 2.1.
Независимо от того, из каких движений состоит сложное движение ре-
жущего инструмента, его скорость делят на две составляющие, из которых
одна называется скоростью резания, а вторая – скоростью подачи. Причем
под скоростью резания понимается составляющая, которая касательная к
траектории резца, а скоростью подачи – перпендикулярная к касательной со-
ставляющая. Иногда в технических приложениях встречаются другие опре-
деления скоростей подачи и резания. Используя их, мы будем в необходимых
случаях делать определенные пояснения.
В зависимости от сочетания простых движений резцов от массива от-
деляются куски породы различных форм и размеров. При этом один расчет-
ный размер – глубина резания (толщина стружки) может быть положен (см.
2.2) в основу расчета сил, действующих на резец со стороны разрушаемой
породы. В случае сочетания различных простых движений резца соответ-
ствующие исполнительные органы снимают стружку, толщина которой
определяется на основе изучения кинематики их движения.

Таблица 2.1 – Классификация движений исполнительных органов
№
п/п
Число простых
движений
Типы простых
движений
Примеры
1 1 поступательное Струг, бульдозер
2 2 поступательное +
поступательное
Ковшовая рама;
цепной бар
поступательное +
вращательное
Шнек-фреза
очистного комбайна;
ковш прямой лопаты;
фрезерный барабан
3 3 поступательное +
два вращательных
Планетарно-дисковый
исполнительный орган;
дренажно-дисковая машина
вращательное +
два поступательных
Ковшовая рама
веерного копания
4 4 поступательное +
три вращательных
Режущие головки тоннелепроход-
ческой машины
При снятии стружки одним простым поступательным движением ее
толщина задается или находится из равновесия или балансовых соотноше-
ний. В тех случаях, когда движение резца состоит из двух поступательных
движений (рис. 2.7,а) толщина стружки зависит от скоростей этих независи-
мых движений и шага установки резцов в линии резания. Для ее определения
рассмотрим план скоростей (рис.2.7,б).
Подобные движения реализуются исполнительными органами экскава-
торов непрерывного действия, а также машинами врубовыми, щеленарезны-
ми и, вообще, машинами с баровыми исполнительными органами.
Рисунок 2.7.
а – к определению толщины стружки
при двух поступательных движениях режущего инструмента;
б - план скоростей резца исполнительного органа,
совершающего два поступательных движения.
v
u λ
h tp
а)
α
α1
u
v
va
б)

Обозначим через v переносную скорость движения исполнительного
органа, а через u относительную скорость движения резцов и определим по-
ступательное перемещение λ исполнительного органа за время τ перемеще-
ния резца на расстояние, равное шугу tp резцов в линии резания
λ=v⋅τ, (2.13)
или с учетом того, что τ=tpu,
u
v
λ=tp⋅ . (2.14)
Так как
h=λ⋅sinα1, (2.15)
где α - угол между скоростью v исполнительного органа и абсолютной vа
скоростью резца.
Из плана скоростей имеем
( ) ( ) α
α
α α
α
α
2 cos
sin
sin cos
sin
sin
1 2 2 2+2+ ⋅⋅
⋅
=
⋅ ++ ⋅
⋅
=
u v uv
u
u vu
u , (2.16)
где α - угол между переносной и относительной скоростями.
Формула (2.16) значительно упрощается при ее использовании в расче-
тах реальных машин с исполнительными органами типа цепного бара и мно-
гоковшовой рамы. Обычно в таких машинах v << u и тогда sinα1≈sinα, а
sinα
u
v
h≈tp . (2.17)
Если режущие элементы исполнительного органа участвуют в поступа-
тельном и вращательном движениях (рис.2.8), то они снимают слой породы
переменной толщины. При этом резцы движутся по траекториям, описывае-
мым линиями, которые называются циклоидами (укороченными или удли-
ненными) (рис.2.9,б). Обычно в таких случаях различают максимальную,
среднюю и минимальную толщину стружки.
Такую стружку снимают режущие элементы наиболее распространен-
ных исполнительных органов горнодобывающих машин – цилиндрических и
шнековых фрез, дисковых фрез торфодобывающих и камнерезных машин и
т.п. (Рис.2.8). В этом случае толщина стружки зависит не только от соотно-
шения переносной v и относительной u скоростей и размеров исполнительно-
го органа, но также и от степени его погружения в породу. При этом разли-
чают встречное (см. рис. 2.9) и попутное фрезерование. Для определения
средней и максимальной толщины стружки рассмотрим перемещения эле-

ментов фрезы за время ее поворота на угол φ между двумя смежными резца-
ми в линии резания. Это время определяется выражением
t=ω⋅z
2π
1 , (2.18)
где ω - угловая скорость вращения фрезы;
z - число резцов в линии резания.
Рисунок 2.8 – Шнек-фреза очистного комбайна
Рисунок 2.9 – Толщина стружки при работе цилиндрической фрезы
v
Н
λ ω
С
R=D/2
ϕ
ϕк
А В
А
а)
λ
hmax

За это время фреза перемещается в направлении скорости v на расстоя-
ние
=vω⋅z
λ 2π. (2.19)
Считая, с небольшой погрешностью, ΔABC прямоугольным находим
максимальное значение толщины стружки при угле контакта, равном ϕк,
h кvωzϕк
λϕ π
max sin 2sin
= ⋅ = ⋅
. (2.20)
Угол контакта фрезы с породой зависит от наружного (по концам рез-
цов) диаметра фрезы и мощности H разрабатываемого слоя породы. Значение
sinφк при ϕк≤π2 определяется выражением
D
DHH
к
2 2
sinϕ= ⋅− , (2.21)
которое следует из рис.2.9.
Таким образом, максимальную толщину стружки при изменении угла
контакта в пределах 0ϕк≤π2 в зависимости от мощности разрабатываемо-
го слоя породы Н можно определить по формуле
⎟
⎠
⎞
⎜
⎝
⎛−
⋅
⋅
− =
= ⋅ D
H
D
H
z
v
D
H
D
H
h v z 1
4 4
2
2
maxω ωπ
π . (2.22)
Эти формулы справедливы и при HD2, т.е. при ϕкπ2. Однако в
этом случае, надо учитывать, что максимальное значение стружки составляет
z
v
h
⋅
⋅
==
ω
maxλ2π и при превышении угла контакта значения π2 толщина
стружки уменьшается.
Для определения среднего значения толщины стружки вычислим пло-
щадь серповидной формы сечения стружки (рис 2.11), снимаемой резцом и
определим её площадь через её среднее значение.
Рисунок 2.11 – К определению среднего значения толщины стружки
v
Н
λ ω
С
R=D/2
φz
φк
А В
А

В первом случае
ϕ
ϕ
s hDd
к
=∫ ⋅
02
, (2.23)
где ϕ
ω
π
2 sin
z
v
h
⋅
⋅
= - текущее значение толщины стружки.
Тогда
D( к)
z
v
D d
z
v
s к π ϕ
ϕϕω
π
ω
ϕ
sin 1cos
2
2
0
=∫ ⋅ ⋅ ⋅= ⋅ ⋅− , (2.24)
а с другой стороны
ср к
D
shϕ
= 2
. (2.25)
Приравняв правые части (2.24) и (2.25) получаем
( к)
к
ср
z
v
h ϕ
ωϕ
π
2 1−cos
⋅⋅
⋅
= . (2.26)
В частном случае при работе фрезы полным захватом, или при поло-
винном заглублении ее, т. е. при ϕк=π2 имеем
z
v
hср
⋅
⋅
=
ω
ϕ , (2.27)
или hср2hmax
=π
, так как в этом случае
z
v
h
⋅
⋅
=
ω
2π
max . (2.28)
В расчетные формулы для определения толщины стружки или глубины
резания входит число z резцов в линии резания. Само понятие линии резания
не вполне определено, так как этих линий при конечной ширине захвата од-
ного резца может быть бесчисленное количество. В свое время Ф.А. Опейко
предложил пользоваться понятием среднего числа резцов в линии резания,
как величины, определяемой выражением
B
bn
z=0⋅ , (2.29)
где b0 – ширина захвата одного резца;
n – общее число резцов на фрезе;
B – общая ширина захвата фрезы.
В этой книге мы будем пользоваться этим определением, но, учитывая
то, что ширина захвата одного резца определяется с учетом развала бороздки
(рис.2.12), определим эту ширинy по формуле

b0=b+2h⋅tgα. (2.30)
где α - угол развала бороздки.
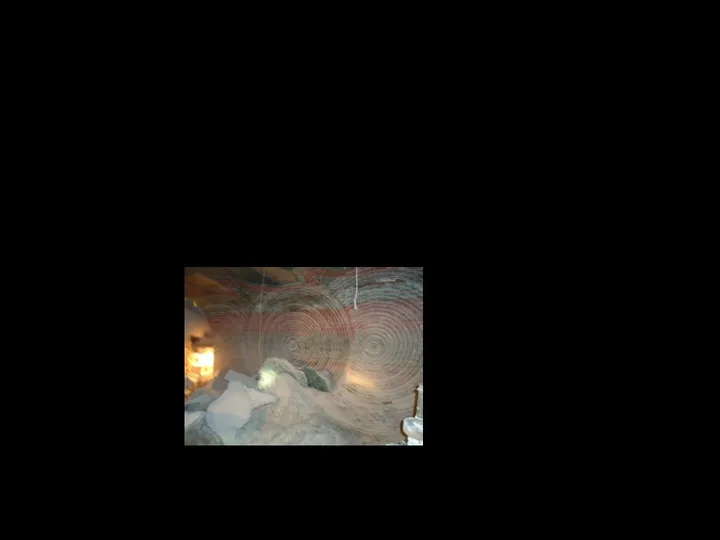
Рисунок 2.12 – К определению ширины захвата резца
Из двух простых движений (поступательного и вращательного) состоит
движение режущих элементов проходческих комбайнов и тоннелепроходче-
ских машин бурового типа. Траектория движения резцов представляет собой
винтовые линии (рис.2.13) различных радиусов
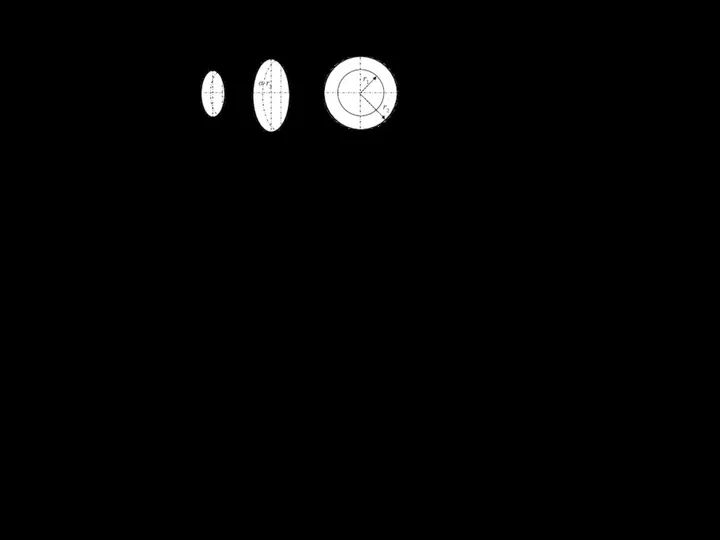
Рисунок 2.13,а – Форма забоя при фрезеровании разрабатываемого пласта
соосными роторами (три косых захода комбайна ПКС-8)
h
b0
b
α

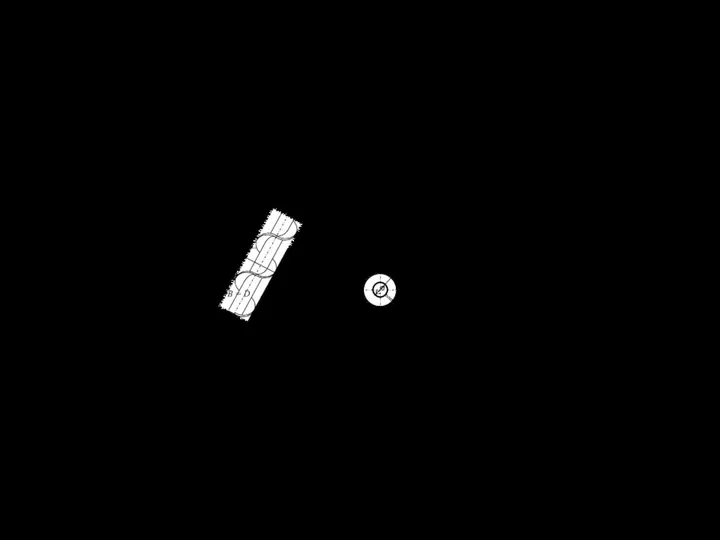
Рисунок 2.13,б – Траектории движения режущих элементов
исполнительного органа бурового типа
Определяя толщину стружки, снимаемую резцами, обозначим, как и
ранее, через vк поступательное перемещение исполнительного органа за
время его поворота на угол между двумя соседними резцами в одной линии
резания. Тогда
z=vω⋅z
λ 2π, (2.31)
а
hr=λzcosα, (2.32)
где hr - толщина стружки, снимаемой резцами, расположенными по линии
радиуса R относительно оси вращения исполнительного органа;
αr - угол между осью вращения исполнительного органа и нормалью к
винтовой линии.
Косинус этого угла (рис.2.14)
Рисунок 2.14 – Схема для определения угла αr
242 2 2 22
2
cos
v r z
r z
r
r
z
r
+ ⋅ ⋅
⋅ ⋅
=
+
⋅
=
ω
ω
λ π
π
α . (2.33)
В большинстве реальных проходческих машин скорость v поступа-
тельного движения намного меньше, чем произведение r·ω·z, поэтому без
большой погрешности, особенно при предварительном проектировании
λ
λ
r1
r2
α·r1 α·r2

можно принимать толщину стружки постоянной для всех резцов в линии ре-
зания и определять ее по приближенной формуле
hz=z=vω⋅z
λ 2π, (2.34)
где индекс z означает, что толщина стружки определяется для линии резания
с числом резцов z.
При этом можно пользоваться и средним значением числа резцов в ли-
ниях резания, которое определяется по формуле (2.24).
В исполнительных органах ряда горных машин, режущие элементы ко-
торых совершают независимые вращательное и поступательное движения,
используются шнек-фрезы, ось вращения которых отклонена от направления
поступательного движения на некоторый угол, обычно равный π/2 или боль-
ше чем π/2 (рис.2.15).
Рисунок 2.15 – Схема взаимодействия резцов шнек-фрезы с породой
Такие исполнительные органы бывают двух типов: с непрерывной ре-
жущей кромкой на наружной поверхности винтовой лопасти, и с отдельными
резцами, расположенными на той же поверхности.
Для определения толщины стружки, снимаемой режущими элемента-
ми, рассмотрим сечение А-А, перпендикулярное оси вращения фрезы. В
плоскости этого сечения траектории движения режущих элементов такие же,
как и у цилиндрической фрезы. Поэтому для определения максимальной и
средней толщины стружки можно пользоваться формулами
α
ω
π
max2 sin
z
v
h
⋅
⋅
= , (2.35)
α
ωsin
4
z
v
hср
= ⋅
, (2.36)
где α – угол между вектором ω и v;
А
А
v
H B = D
А - А
α
d
ω

z – среднее число резцов в линиях резания шнек-фрезы второго типа,
или число заходов шнек-фрезы с непрерывной режущей кромкой. Формулы
(2.31) и (2.32) вытекают из формул (2.24) и (2.26) при ϕк=π2 и учете угла
между векторами ω и v.
Два вращательных и одно поступательное движения осуществляются
режущими элементами проходческо-добычных комбайнов с, так называе-
мым, планетарно-дисковым органом разрушения (рис.2.16,а). В наиболее
распространенных проходческих комбайнах семейства «Урал» траектории
движения резцов представляют собой винтовые кривые на поверхности ова-
лообразного тора (рис.2.16,б и в).
Рисунок 2.16 – Вид спереди (со стороны забоя) на сдвоенный планетарно-
дисковый исполнительный орган проходческо-очистного комбайна
Диски, на которых расположены резцы, вращаются с угловой скоро-
стью ω1 вокруг собственных осей, которые в свою очередь движутся по вин-
товым линиям, вращаясь вокруг оси 0y с угловой скоростью ω2. В свою оче-
редь, весь исполнительный орган совершает поступательное движение со
скоростью v1. Таким образом, переносное движение резцов является слож-
ным и включает одно поступательное и одно вращательное движения, а от-
носительное движение – вращательное с угловой скоростью ω2. Окружные
скорости в относительном и переносном вращениях, даже при постоянных
значениях угловых скоростей непрерывно меняют свои направления в про-
цессе взаимодействия режущих элементов с породой. В следствие этого ме-
няется и результирующая скорость. Угол контакта резцов с породой состав-
ляет 180о. Внутри этого угла относительная окружная скорость меняет свое
направление на противоположное, а переносная окружная скорость изменя-
ется в пределах от ω1(R1+R2) до ω1(R1−R2), где R1 – радиус, на котором рас-
положены оси вращения дисков; R2 – радиус дисков по концам, установлен-
ных на них резцов.

Рисунок 2.16 (б,в) – Форма забоя и траектории движения резцов
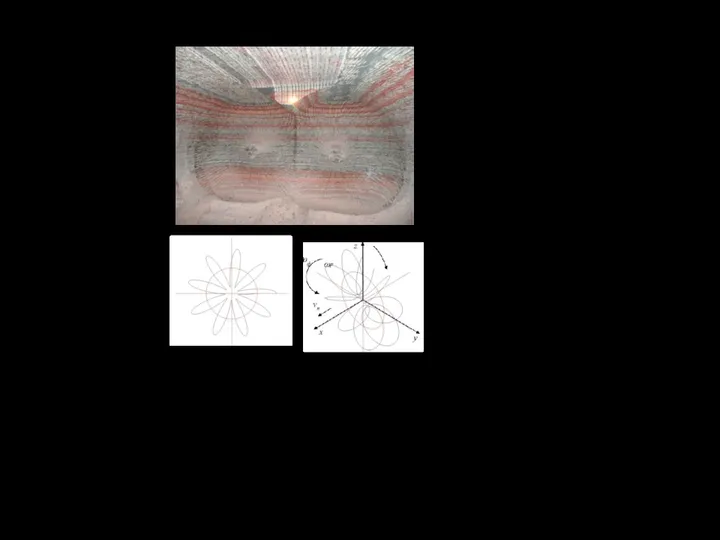
планетарно-дискового исполнительного органа
Третья составляющая скорости – поступательная скорость перемеще-
ния всего исполнительного органа в стационарном режиме работы выемоч-
ной машины остается постоянной как по величине, так и по направлению.
Поэтому в этом случае (рис.2.17) можно различать продольную и боковую
скорости подачи режущего элемента.
Передняя стружка имеет переменную от нуля до hmax толщину и может
быть определена так же, как и для цилиндрической фрезы
22
max
2
h=vω⋅z
π , (2.37)
х
у
z
vп
ωф ωр

где величины v, ω2, z2 имеют тот же смысл, что и в формулах (2.26) и (2.27).
При этом средняя толщина стружки
2z2
l
hсрv p
=ω⋅
. (2.38)
Рисунок 2.17 – К определению толщины стружки
планетарно-дискового исполнительного органа
Что касается боковой толщины стружки, то она является постоянной и
определяется через параметры угловых скоростей переносного и относитель-
ного вращений следующим образом
22
11
2
hб= ⋅Rω⋅z
π
ω . (2.39)
Конечно, полученные зависимости для определения толщины стружки
ряда исполнительных органов выемочных машин не охватывают всех прин-
ципов таких органов и тем более всех видов движений их режущих элемен-
тов. Однако они дают возможность в необходимых случаях найти параметры
стружки, снимаемой исполнительными органами других конструкций. В со-
ответствующих разделах мы будем прибегать как к выше приведенным фор-
мулам, так и будем определять на их основе параметры стружки в тех случа-
ях, когда режущие элементы совершают более сложные движения.
z
x y
ωф1 ωp
ωф2
h
h

3. УРАВНЕНИЯ ДВИЖЕНИЯ ГОРНЫХ МАШИН
3.1 Способы составления уравнений движения
Прогнозирование состояния горной машины, а также её энергетиче-
ские, нагрузочные и прочностные расчёты базируются на основе общих за-
конов сохранения и уравнений движения механики. Среди законов сохране-
ния чаще всего используются материальные и энергетические, которые вы-
ражаются посредством уравнений балансов мощности, производительности,
тепла и т. д. Уравнения движения горных машин составляются в виде урав-
нений движения механических и электромеханических систем. Они обычно
представляются в форме уравнений Лагранжа 2-го рода, Аппеля и некоторых
специальных систем уравнений Лагранжа, а также в некоторых случаях
уравнения Аппеля. В целях облегчения усвоения материала приведем здесь
эти системы уравнений.
Уравнения Лагранжа 2-го рода обычно записываются в виде
i
i i
Q
дq
дТ
дq
дТ
dt
d ⎟⎟− =
⎠
⎞
⎜⎜
⎝
⎛

, (3.1)
где Т - кинетическая энергия машин, выраженная через обобщенные скоро-
сти и координаты;
qi, qi - обобщённые координаты и скорости машины;
Qi - число обобщённых координат.
Уравнения Аппеля записываются следующим образом
i
i
П
д
дS=
π
, (3.2)
где S - энергия ускорений системы, выраженная через квазиускорения;
πi - квазиускорения;
Пi - квазиобобщённые силы;
i=1,n , где n - число степеней свободы системы.
На практике, кроме систем уравнений (3.1 и 3.2) и аналогичных им
применяются системы уравнений, получаемые при использовании принципа
Даламбера. Как известно, использование этого принципа базируется на до-
бавлении к внешним силам, действующим на машину, сил инерции и состав-
ления уравнений равновесия с учётом этих сил.
Не останавливаясь на способах формирования этих систем, отметим
лишь, что выбор той или иной формы уравнений движения определяется
удобством их использования. Примеры их составления и анализа даны в со-
ответствующих разделах. Приведенные системы обычно представляют собой
системы обыкновенных дифференциальных уравнений второго порядка и

используются для изучения динамических процессов работы горных машин.
Изучение стационарных режимов работы, т. е. режимов работы с постоян-
ными скоростями движения машин и их механизмов чаще всего базируется
на уравнениях, выражающихся уравнениями равновесия, балансовыми соот-
ношениями по мощности, производительности, теплу и т. п. Уравнения рав-
новесия представляют собой уравнения статики механических систем и обра-
зуются из систем (3.1 и 3.2) путём приравнивания к нулю их левых частей.
Среди балансовых соотношений наиболее часто используются уравнения ба-
лансов мощности и производительности. Уравнение баланса мощности в об-
щем случае может быть записано в форме
Nij
mn
nij
n
∑Nдi=∑∑N ⋅K
1 11
, (3.3)
где Nдi - мощность i-го двигателя, установленного на машине;
n - число двигателей;
Nnij - мощность, потребляемая j-м механизмом машины от i -го двигателя;
m - число механизмов, потребляющих энергию;
KNij - коэффициент запаса прочности.
Это уравнение формируется для каждой машины и чаще всего, в виде
системы уравнений, так как баланс мощности должен соблюдаться для каж-
дого двигателя в отдельности. Несмотря на кажущуюся его простоту, урав-
нение успешно используется для решения целого ряда задач, включающих
подбор двигателей, определение скоростей работы механизмов и, в конечном
счёте – нахождение теоретической производительности машины в конкрет-
ных условиях эксплуатации.
Наряду с уравнением баланса мощности для рационального, а иногда, и
оптимального выбора параметров и режимов работы механизмов машины в
расчётной практике используют также уравнения баланса производительно-
сти, которые записывают в виде
i Qi i
ОВ Q x
QKQ
QКQ
= ⋅
= ⋅
+1
, (3.4)
где Qx – производительность машины по ходу;
QОВ - производительность выемочных исполнительных органов горной
машины;
Qi+1, Qi – производительности последовательных механизмов погрузки,
транспортирования и других устройств перемещения породы;
КQ, КQi – соответствующие коэффициенты запаса.
В записанных формулах имеется в виду объёмная производительность,
хотя соотношения справедливы и для производительности, выраженной в
других единицах.

3.2 Основные методы исчисления производительности
и потребляемой мощности
Мощность энергетических установок горных машин, а также их произ-
водительность являются одними из важнейших технических параметров и,
как правило, приводятся в технических характеристиках, которые служат од-
ним из документов, сопровождающих процесс создания и жизненного цикла
машины.
В не меньшей мере это относится и к такой величине, как производи-
тельность. В совокупности эти параметры определяют такой критерий каче-
ства машины, как энергоэффективность.
В этой связи определение их расчётных значений и анализ представля-
ют одну из основных задач, решаемых на этапе выбора технических предло-
жений создания машины.
Производительности различают объёмную и массовую. Они связаны
соотношением
G=ρ⋅Q , (3.5)
где Q - объёмная производительность;
ρ - плотность разрабатываемой породы;
G – массовая производительность.
Объёмная и массовая производительности выражаются различными
соотношениями.
Для горных машин периодического действия
tц
V
Q= , (3.6)
где V – объём породы, вынимаемой за время рабочего цикла;
tц – время совершения цикла.
Для машин непрерывного действия
Q=F⋅v , (3.7)
где F – площадь поперечного сечения разрабатываемого слоя породы;
v – скорость движения исполнительного органа, нормальная к площади F.
Эти выражения чаще используются для определения объёмной произ-
водительности по ходу. Производительность исполнительных органов выра-
жается с учётом параметров и изменения физико-механических свойств по-
роды в процессе её разрушения. В первую очередь изменение свойств поро-
ды учитывается, так называемым, коэффициентом Kp разрыхления. При по-
мощи этого коэффициента учитывается изменение объёма породы и её плот-
ности после разрушения

V
V
Kp=p ;
pKp
ρ
ρ= , (3.8)
где Vp - объём породы после её разрушения;
V - объём породы в массиве до разрушения;
ρр - плотность разрыхленной породы;
ρ - её плотность в массиве.
Производительность основных типов исполнительных органов горных
машин по ходу обычно приводится к производительности V, что удобно для
проверки соотношений (3.4), тогда её можно выразить следующими соотно-
шениями:
- для исполнительного органа типа цепного бара
p
V
цб иоK
K
Q.=F.⋅u⋅ , (3.9)
где u – скорость цепи;
Fи.о - площадь поперечного сечения породы, передвигаемой цепным ба-
ром;
b - ширина захвата цепного бара;
hp - вылет резцов;
h - глубина резания;
KV - коэффициент заполнения породой рабочего пространства бара;
Kp - коэффициент разрыхления породы;
- для цилиндрической и дисковой фрезы
( ) ( )ω
π
π ω
= − = D−dB⋅
K
K
DdB
K
K
Q
p
V
p
V
цф
2 2
2 2
. 8
1
4 2
, (3.10)
где D - диаметр фрезы по концам ножей;
d - диаметр, на котором установлены режущие элементы фрезы;
B - её ширина;
ω - угловая скорость вращения;
- для шнек-фрез, перемещающих породу вдоль оси необходимо наря-
ду с условием (3.9) выполнение дополнительного условия, заключающегося в
том, чтобы производительность по перемещению разрыхлённой породы была
большей, чем производительность по разрушению породы. Производитель-
ность по разрушению породы может быть рассчитана по формуле (3.10), а
производительность по перемещению - по формуле
( )
oc
н в
p
V
пф v
dd
K
K
Q
4
2 2
.
−
= π , (3.11)

где dн - наружный диаметр витков транспортирующей части шнек-фрезы;
dв - диаметр корпуса транспортирующей части шнек-фрезы;
voc=hвω⋅Кц
2π
- осевая скорость перемещения породы шнек-фрезой;
Kц - коэффициент циркуляции породы в транспортирующей части шнек-
фрезы (коэффициент, учитывающий вращение породы вместе со шнеком
(коэффициент циркуляции).
Окончательно, производительность шнек-фрезы по перемещению раз-
рыхлённой породы
Qп.ф=(dн2−dв2)hв⋅ω⋅Кц
8
1 , (3.12)
- для ковшовой рамы
u
t
V
K
К
Q
к
к
p
к.р=V ⋅ , (3.13)
где Vк - объём ковша;
tк - шаг установки ковшей;
u - скорость их движения.
Конечно, записанные формулы исчисления производительности не яв-
ляются единственно возможными способами её определения и не охватыва-
ют всех других методов нахождения производительности исполнительных
механизмов горных машин.
При вычислении потребляемой механизмом мощности обычно поль-
зуются известными из механики определениями мощности:
- скалярного произведения векторов силы и линейной скорости,
- момента и угловой скорости,
а также другими зависимостями, вытекающими из них. В инженерной
практике наиболее широко распространена формула
N=e⋅Q , (3.14)
где е - удельные затраты мощности для работы того или другого механизма
или устройства;
Q - его производительность.
Эта формула, как указывалось в главе 2, применяется для определения
мощности на разрушение горных пород. Вместе с тем, она используется и
для вычисления затрат мощности на работу любых механизмов. Величина
удельных затрат мощности чаще всего определяется опытным путем. Однако
существуют и различные способы её определения расчётами по функцио-
нальным, феноменологическим или эмпирическим формулам. Например, при
разрушении горных пород механическим резанием мы очень часто будем ис-
пользовать формулу (2.5).

4. МЕХАНИЗМЫ ПЕРЕМЕЩЕНИЯ ГОРНЫХМАШИН
И ПОДАЧИ ИХ ИСПОЛНИТЕЛЬНЫХ ОРГАНОВ НА ЗАБОЙ
4.1 Общие сведения
Для большинства горных машин взаимодействие с горными породами
осуществляется посредством их разрушения исполнительными органами, а
также воздействием опорно-ходовых устройств на несущее основание. Все
нагрузки, воспринимающие при работе исполнительных механизмов, а также
по причине воздействия на машину сил другой природы (атмосферные
нагрузки, силы тяжести и инерции), так или иначе, передаются на опорно-
ходовые устройства. Существуют много различных конструкций таких
устройств – колесные и гусеничные механизмы перемещения, шагающие
движители, цепные, канатные и гидравлические механизмы подачи, а также
различные сочетания перечисленных механизмов. В некоторых машинах их
перемещение и подача исполнительных органов на забой осуществляется од-
ним и тем же механизмом. В качестве таких механизмов чаще всего исполь-
зуются колесные и гусеничные движители. Например, проходческие комбай-
ны, бульдозеры, погрузчики и т.п.
При разработке угольных и соляных месторождений подземным спо-
собом в качестве выемочных машин используются очистные комбайны, ко-
торые перемещаются вдоль забойного конвейера специальной системой по-
дачи. Эта система одновременно перемещает комбайн и создает усилия, не-
обходимые для подачи исполнительного органа на забой. То же самое отно-
сится и к многоковшовым экскаваторам непрерывного действия и некоторым
другим горным машинам. В машинах, осуществляющих рабочие процессы в
стационарных или полустационарных состояниях, подача исполнительного
органа на забой производится специально для этого установленными меха-
низмами. Классическим примером таких механизмов является механизм
напора одноковшовых экскаваторов типа прямая лопата. Существует до-
вольно большое разнообразие конструкций таких механизмов, среди которых
наиболее распространены канатные, реечные, кремальерные гидравлические
и рычажные.
Горные машины работают в самых различных условиях. Это наклады-
вает определенные требования на их механизмы перемещения: по проходи-
мости, маневренности, сцепным свойствам. Это относится и к наиболее рас-
пространенным гусеничным и колесным опорно-ходовым устройствам, кото-
рыми чаще всего оснащены мобильные горные машины. Ходовые механизмы
горных машин взаимодействуют с опорными основаниями, отличающимися
по своим прочностным и другим физико-механическим свойствам в сотни и
тысячи раз. Например, торфяные машины для подготовки месторождений
работают в условиях низкой несущей способности опорного основания (до-
пускаемые давления составляют величину порядка 10 кПа, а машины для до-
бычи высокопрочных каменных пород работают при давлениях на опорное
основание порядка десятков МПа.

Как большое разнообразие условий работ горных машин, так и огром-
ное число конструкций их движителей не позволяет охватить едиными зако-
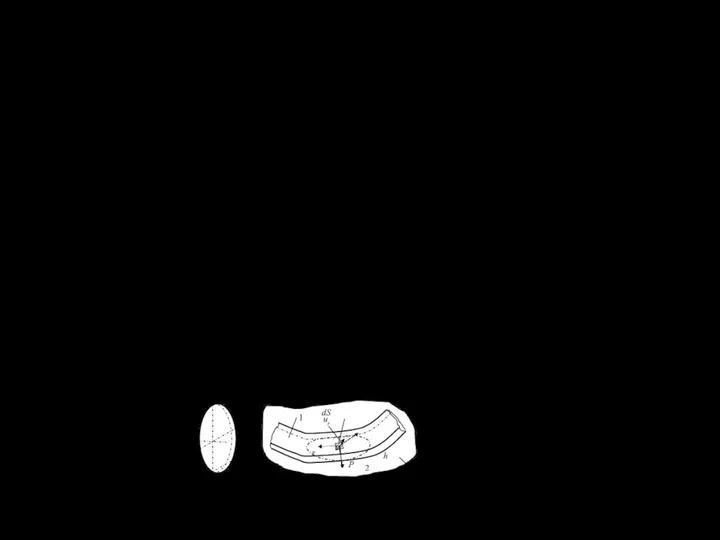
номерностями взаимодействие их с опорными основаниями. Поэтому в
настоящей книге с целью единого подхода к процессам взаимодействия хо-
довых устройств с опорными основаниями выделяются следующие ситуации:
- деформируемое опорное основание – жесткий движитель (слабые
грунты – металлический гусеничный ход, жесткие колеса; опорная база ша-
гающего движителя);
- деформируемое опорное основание – жесткий движитель (железнодо-
рожный ход, гусеничный ход на скальных породах);
- жесткое опорное основание – деформируемый движитель (пневмати-
ческий колесный ход на дорогах с твердым покрытием или скальных поро-
дах);
- деформируемое опорное основание – деформируемый движитель
(пневмоколесный ход в условиях бездорожья).
Под жесткими опорными основаниями и ходовыми устройствами по-
нимаются не абсолютно твердые тела, а полупространства, деформации ко-
торых пренебрежительно малы по сравнению с их характерными размерами,
и наоборот, деформируемыми считаются такие опорные основания и ходо-
вые устройства, деформации которых сопоставимы с характерными размера-
ми движителей и учитываются при их расчетах.
4.2 Трение между движителем и опорным основанием
Рассмотрим взаимодействие контактной площадки движителя с несу-
щим основанием. Наружные поверхности колесных и гусеничных движите-
лей периодически вступают во взаимодействие с опорной поверхностью и
воспринимают при этом реакции последней. Контактные площадки движите-
лей могут иметь различную форму от прямоугольной у гусеничных и колес-
ных машин на жестких колесах до круглой или овальной - у машин на пнев-
матических колесах.
Рассмотрим плоскую контактную площадку, нагруженную нормальной
нагрузкой Р и касательным к нет усилием Т. на этой площадке выделим эле-
мент площади ds, нагруженный давлением р и касательным напряжением τ
(рис.4.1).
Рисунок 4.1 – К определению силы трения
между движителем и опорной поверхностью
1 dS
P
τ v
ur
h
2

Если движитель скользит относительно опорной поверхности , то каса-
тельное напряжение между ними с учетом его противоположного направле-
ния можно определить формулой
v
v
τ=−f⋅p , (4.1)
где f – коэффициент трения;
v – скорость скольжения движителя относительно опорной поверхности.
Эту скорость можно считать суммой двух скоростей, первая из которых
– переносная, есть скорость скольжения всей контактной площадки движи-
теля. Вторая составляющая скорость – относительная скорость возникает по
нескольким причинам. К таким причинам, прежде всего, относятся различная
величина смещений контактирующих точек движителя и опорной поверхно-
сти, вызванных нормальным давлением и другими причинами. Как визуаль-
ные наблюдения за взаимодействием ходовых устройств с опорными основа-
ниями, так и многочисленные эксперименты показывают, что помимо нор-
мальных к опорной поверхности и продольных деформаций (деформаций в
направлении движения) соприкасающиеся элементы движителя и опорного
основания испытывают и поперечные деформации. Величина этих деформа-
ций зависит от физико-механических свойств материалов движителя и опор-
ной поверхности, а также нагрузок между ними и скоростью их приложения.
Особенно наглядно это проявляется при движении мобильных машин по
грунтам с малой несущей способностью (болото, грунтовая дорога). Если фи-
зико-механические характеристики прочности материала движителя и опор-
ного основания высоки, то поперечные деформации незначительны и ими
чаще всего можно пренебречь, что обычно и делается. Однако, если они су-
щественны и сопровождаются различными смещениями точек движителя и
опорного основания, то на преодоление трения между ними в поперечном
направлении затрачивается определенная мощность, зависящая как от вели-
чины сил трения, так и скоростей смещения. В первом приближении примем,
что поперечные деформации связаны с нормальными посредством закона
Пуассона и перемещения контактирующих точек движителя и опорной по-
верхности по направлению совпадают, а трение между ними подчиняется за-
кону Кулона. При таких предположениях эпюры напряжений между движи-
телем и опорной поверхностью можно качественно представить так, как на
рис.4.2.
Пользуясь известными соотношениями, определим основные величи-
ны, представленные на рис.4.2, и зависимости между ними. Эпюра нормаль-
ных давлений между движителями и опорным основанием может иметь раз-
личную форму в зависимости от типа движителя и характера распределения
внешних нагрузок, в первую очередь, сил тяжести.

Более подробно характер распределения давлений и деформаций дви-
жителя и опорного основания рассматривается в разделах, посвященных
конкретных механизмов перемещения.
Рисунок 4.2 – Эпюры и схемы некоторых характеристик взаимодействия
движителя с опорной поверхностью:
а) – эпюра нормальных давлений; б) – переносная и относительная скорости;
в) – относительные деформации; г) – относительные скорости.
В соответствии с ранее принятыми допущениями принимаем, что по-
перечные и нормальные относительные деформации движителя и опорного
основания связаны закономерностью Пуассона
ε′=μ⋅ε, (4.2)
где ε′ - относительная поперечная деформация;
μ - коэффициент Пуассона;
ε - нормальные к поверхности контакта движителя и опорного основа-
ния относительные деформации, а величина ε подчиняется закону Гука
ε=pE, (4.3)
где E - модули упругости контактирующих сред.
а)
б)
в)
г)
р
uк
ε, ε’
dp
v

Обозначив через l1′ и l2″ смещения контактирующих точек движителя
и опорного основания в плоскости последнего, запишем (4.2)
dt
dl
dt
dl
uк
′
−
′
=1 2, (4.4)
и учитывая, что
dt
dl
dt
dl′=μ , (4.5)
а
dt
dp
E
l
dt
dp
l
dp
d
dt
dp
dp
dl
dt
dl
= ⋅=ε = (4.5)
где l - размер деформируемых частей движителя и опорного основания по
нормали к последнему, имеем после подстановки (4.5) в (4.4)
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
= −
2
2
2
1
1
1 E
l
E
l
dt
dp
ur μ μ . (4.6)
Вычисляя продольную составляющую силы трения между движителем
и опорным основанием, запишем
∫∫
+
= ⋅
s c rx
c dS
vu
v
T fp
2 2
. (4.7)
Так как по условию f и vc постоянны, то (рис.4.2)
∫∫
+
= ⋅
s c rx
c dS
vu
p
T fv
2 2
. (4.8)
В этом интеграле давление р и составляющие относительной скорости
выражаются как некоторые функции координат площади контакта. Однако,
если вместо подставить ее некоторое усредненное значение, то сила трения
между движителем и опорной поверхностью
2 2
c rx
c
z
vu
v
T fP
+
= ⋅ , (4.9)
так как ∫∫ =
s
pdSPz
где Pz - сила нормального давления движителя на несущее основание.

При использовании для вычисления силы трения формулы (4.9) необ-
ходимо иметь в виду, что усредненное значение составляющей относитель-
ной скорости должно удовлетворять условию
∫∫
+
=
s + c rc
z
c rx vu
P
vu
pdS
2 2 2 2
. (4.10)
Анализируя формулу (4.6) следует отметить, что величина относитель-
ной скорости зависит от основных механических характеристик опорного
основания и материала движителя, а также скорости изменения давления
между ними. Учитывая это, а также то, что изменение давления по времени
сопровождается его изменением по площади контакта и зависит от нормаль-
ной нагрузки, т. е.
dt
dy
y
p
dt
dx
x
p
dt
dp
∂
∂
+
∂
∂
= , (4.11)
где x, y - координаты контактной площадки, причем =0
dt
dx ; v
dt
dy=,
v - скорость перемещения движителя, примем, что upc пропорциональна
нормальному давлению и скорости движения
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
∂
∂
=
2
2
2
1
1
1 E
l
E
l
v
y
p
urc μ μ . (4.12)
Так как
y
p
∂
∂ определяет распределение нагрузки по длине контактной
площади между движителем и опорным основанием, то, приняв производ-
ную пропорциональной величины давления, получим
urc=k⋅p⋅v, (4.13)
где k - некоторый коэффициент пропорциональности, учитывающий вели-
чину давления и физико-механические свойства движителя и опорного осно-
вания (коэффициент, конечно, требует экспериментального определения).
Таким образом, формулу (4.9) в окончательной форме представим сле-
дующим образом
2
2
2
2 2
2 2 22
v
S
P
v k
v
fP
v kPv
v
T fP
z
c
c
z
c
c
z
+
= ⋅
+ ⋅ ⋅
= ⋅ (4.14)

и будем пользоваться ею при определении силы трения между ходовыми
устройствами горных машин и несущими основаниями. Эта формула дает
нелинейную зависимость между силой трения и скоростью скольжения кон-
тактной площадки движителя, которая качественно представлена на рис.4.3.
Рисунок 4.3 – Зависимость силы трения от скорости скольжения
Из (4.13) видно, что при возрастании vc до значений на много больших,
чем произведение k⋅p⋅v значение силы трения совпадает со значением, ко-
торое дает формула Кулона. Кроме того, эта формула показывает, что сила
трения нелинейно зависит от нормальной нагрузки на движитель и размеров
его контакта с опорным основанием. При получении этой формулы приняты
ряд допущений о форме поверхности контакта и упругих свойствах материа-
лов движителя и опорного основания. Что делает ее приближенной. Тем не
менее, она дает возможность оценки некоторых факторов на величину силы
трения.
Т
f·Pz

4.3 Колесные опорно-ходовые устройства горных машин
4.3.1 Колесо транспортного средства
Колесо транспортного средства – элемент движителя, состоящий из те-
ла вращения, связанного с рамой машины посредством центральной оси,
опирающегося оболочкой качения на несущее основание и предназначено
для преобразования вращательного движения в поступательное.
Основная цель применения колес на транспортных средствах или на
мобильных технологических машинах состоит:
∙ в активном режиме – преобразование приводного (крутящего)
момента от двигателя в Мкр в тяговое усилие РТ;
∙ в пассивном – обеспечение минимального сопротивления движе-
нию μ прицепного (ведомого) модуля;
∙ направляющие – для управления направлением движения маши-
ны.
Тело качения по внешней оболочке может представлять собой:
1. цилиндр;
2. усеченный конус, в т.ч. спаренный;
3. центральный сегмент сферы или элипсоида вращения;
4. тор;
5. многогранная прямая призма.
Оболочка качения бывает условно жесткая и упругая (деформируе-
мая).
Современные колеса транспортных средств и большинства технологи-
ческих машин имеют пневматические шины.
По наличию на внешней оболочке элементов сцепления с опорным ос-
нованием колеса бывают:
1. гладкие;
2. с плотным протектором;
3. со специальным протектором;
4. с развитыми грунтозацепами;
5. с направляющими ребордами или канавками.
В зависимости от количества степеней свободы опорной оси относи-
тельно рамы машины:
1. жестко закрепленное;
2. с упругой подвеской;
3. на качающемся рычаге;
4. с вертикальной, свободной осью поворота (рояльное);
5. направляющее, т.е. с рулевым механизмом поворота.
Опорное основание в зависимости от фи-
зико-механических свойств:
∙ жесткое;
∙ деформируемое.

4.3.2 Комплектность и устройство шины
Пневматические шины являются одним из основных элементов колес.
В процессе эксплуатации транспортных и технологических машин шины
обеспечивают заданную грузоподъемность, устойчивость и управляемость на
всех заданных скоростях, на мокрых и заснеженных дорогах, а также на тех-
нологических поверхностях, улучшенные тормозные характеристики и высо-
кую комфортабельность при минимальном расходе топлива и шумообразо-
вании.
В комплект пневматической шины
входят: - покрышка;
- ездовая камера с вентилем;
- ободная лента (для грузовых).
По конфигурации профиля попе-
речного сечения, т.е. от соотно-
шения высоты профиля (Н) к ши-
рине (В), подразделяются на:
- шины обычного профиля;
- широкопрофильные;
- низкопрофильные
- сверхнизкопрофильные.
Покрышка включает: каркас, брекер, протектор, боковины, борта.
Каркас – основа покрышки с одним или несколькими слоями обрези-
ненного корда с резиновыми прокладками.
Брекер – внутренняя деталь покрышки; расположен между каркасом и
протектором; предназначен для смягчения ударных нагрузок при движении.
Протектор – наружная резиновая беговая часть покрышки с рисунком
или развитыми грунтозацепами; обеспечивает сцепление с дорогой или
опорным основанием и предохраняет каркас от повреждений.
Боковина – наружная резиновая деталь покрышки по боковым поверх-
ностям; основной упругий элемент; предохраняет каркас от боковых наруж-
ных повреждений.
Борт – жесткая часть покрышки, обеспечивающая ее надежное крепле-
ние на ободе колеса.
По способу герметизации различают камерные и бескамерные шины. В
бескамерных шинах по внутренней поверхности каркаса выполнен гермо-
слой с заплечиками в зоне бортов.

4.3.3 Конструкции шин
По типу конструкции различают диагональные и радиальные шины.
ДИАГОНАЛЬНЫЕ
В каркасе диагональных шин нити
корда каркаса и брекера в смежных
слоях перекрещиваются и имеют в
средней части беговой дорожки углы
наклона от 450 до 600 по отношению к
продольной оси.
РАДИАЛЬНЫЕ
В радиальных шинах:
нити корда в каркасе расположены по
меридиану под углом, близким к 00,
в брекерном поясе нити идут под уг-
лом не менее 650, перекрещиваясь
между собой в параллельных слоях.
Брекер в современных шинах изготав-
ливается из металлокорда.
Радиальные шины в настоящее время получили наибольшее
применение на всех категориях транспортных средств, т.к. характеризуются
повышенным пробегом, улучшенным сцеплением с дорогой, пониженным
теплообразованием, низким сопротивлением качению, что в сочетании с
уменьшенной массой позволяет сократить расход топлива.
Перспективной конструкцией считается цельнометаллическая шина
типа (ЦМК), в которой каркас и брекер выполнены из металлокорда.

4.3.4 Обозначение и назначение шин
1 – товарный знак
предприятия-изготовителя;
2 – фирменное обозначение;
3 – размеры шины, в мм (дюймы);
4 –модель шины;
5 – конструкция (радиальная);
6 – нормативный документ;
7 – камерная (бескамерная);
8 – дата изготовления;
9 – знак официального утверждения;
10 – допускаемое давление в шине;
11 – страна- изготовитель;
12 – индекс несущей способности;
13 – индекс скорости.
Индекс несущей способности (ИНС) – одно или два числа, указыва-
ющие нагрузку, которую может выдержать одиночная или сдвоенная шина
при скоростях, соответствующих надлежащей категории скорости. Ряд ИНС
состоит из 200 чисел (0÷199) с диапазоном нагрузок (45÷13600) кг:
ИНС 0 4 10 20 28 42 52 76 108 132 156 199
кг 45 50 50 80 100 150 200 400 1000 2000 4000 13600
Категория скорости – это указанная с помощью условного обозначе-
ния скорость, при которой шина может выдержать нагрузку соответствую-
щим ИНС. Ряд категорий скорости включает 29 позиций (скорость от 5 до
свыше 270 км/ч):
Кате-
гор.
А1-
А8
B C E G J K L P S U V W Z
км/ч 5-40 50 6
0
70 90 10
0
110 12
0
150 18
0
200 24
0
27
0
>27
0
По основному назначению, т.е. по комплектованию движителей
транспортных средств или технологических машин они подразделяются на:
- шины для автомобилей большой и особо большой грузоподъемности;
- шины для строительных, дорожных и подъемно-транспортных машин;
- шины для тракторов и сельскохозяйственных машин;
- шины для грузовых автомобилей и автобусов;
- шины для легковых и легкогрузовых автомобилей;
- шины для велосипедов и мотоциклов.
1
12
5
9
2
13
10
3
4
6
7
8
11

4.3.5 Режимы движения колеса
ВЕДОМЫЙ
rк w О – ось вращения колеса; Ок- ось условного колеса
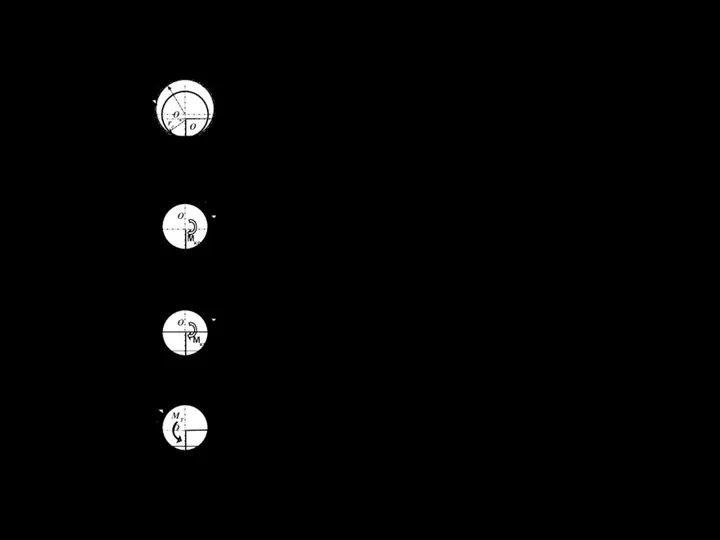
ω G=mg – нормальная нагрузка, Н
F – тяговое (толкающее) усилие, Н
F μ= F / G – коэффициент сопротивления движению
rс и rк – статический и кинематический радиусы, м
ω - угловая скорость, рад/с
Движение с некоторым скольжением ε (rк>rс)
G w=ωrк=ωrс(1+ε), - поступательная скорость, м/с
ВЕДУЩИЙ
w G – нормальная нагрузка, Н
Мкр – приводной (крутящий) момент, Н.м
ω ϕ=[РТ]/ G – коэффициент сцепления (max)
rк и rс – кинематический и статический радиусы
ω - угловая скорость, рад/с
Движение с некоторым буксованием δ, (rк< rс)
PТ w0=ωrс – теоретическая (кинематическая) скорость, м/с
G w=ωrк=ωrс(1-δ), - поступательная (действительная)скорость, м/с
ТЯГОВЫЙ
w G – нормальная нагрузка, Н
Мкр – приводной (крутящий) момент, Н.м
ω Ркр – крюковое сопротивление, Н
Ркр ϕ=[РТ]/ G – коэффициент сцепления (max)
rк и rс – кинематический и статический радиусы, м
ω - угловая скорость, рад/с
Движение с некоторым буксованием δ, (rк< rс)
G w=ωrк=ωrс(1-δ), - поступательная (действительная)скорость
ТОРМОЖЕНИЕ
а w G – нормальная нагрузка, Н
Р – тяговое (толкающее, инерционное) усилие, Н
ω МТ – тормозной момент, Н.м
Р w - поступательная скорость, м/с
ω - угловая скорость, рад/с; при ω=0 – «юз»
а – ускорение (замедление), м/с2
Движение со скольжением ε и замедлением а, (rк>rс)
G Характеризуется временем торможения и тормозным путем
Ок
О
О
О
rc
Мкр
Мкр
МТ
О

4.3.6 Особенности и режимы движения колес
Колесные движители в виду их распространения во всех сферах народ-
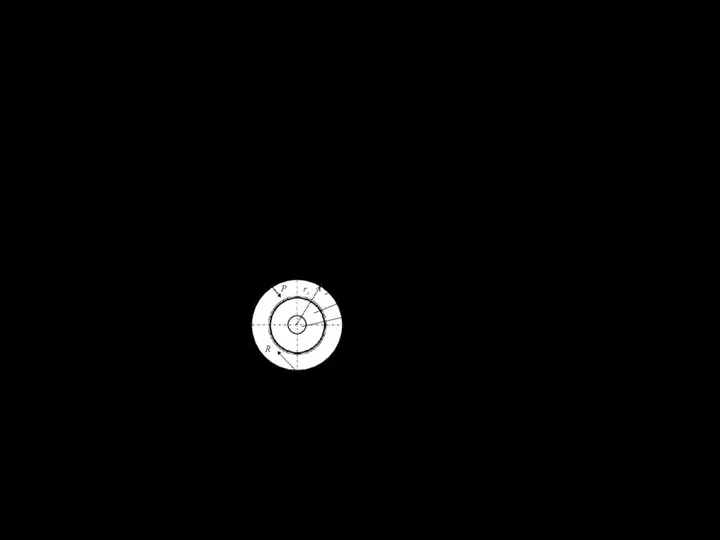
ного хозяйства и высоких эксплуатационных качеств находят самое широкое
применение в горных машинах для выполнения самых различных работ.
Основным элементом колесных движителей является колесо. Колеса
классифицируются по различным признакам: конструкции, режимы и усло-
вия работы, назначение и т.д. различают колеса:
- пассивные (ведомые);
- активные (ведущие);
- жесткие;
- деформируемые.
Все колеса могут работать в различных режимах в зависимости от ве-
личин и соотношения нагрузок, действующих на них, а также от кинематиче-
ских характеристик движителя. Кинематические характеристики движителя
колеса обычно включают: действительную и теоретическую скорости, угло-
вую скорость вращения, радиус качения, угол увода и некоторые другие па-
раметры, которые используются теории автомобильного транспорта, где ча-
ще всего используются упругие пневматические колеса.
Для выяснения физического смысла некоторых характеристик движе-
ния колес рассмотрим прямолинейное движение пневматического колеса
(Рис. 4.4)
Рисунок 4.4 – Прямолинейное движение пневматического колеса
и его основные элементы: 1 – ступица; 2 – обод (дик); 3 – шина
Ступицей колеса называют подшипниковый узел, служащий для пере-
дачи на него сил со стороны рамы машины и обеспечивающей передачу этих
сил посредством тел качения. Обод – промежуточная, чаще всего жесткая,
конструкция между ступицей и шиной, служащая для установки на ней ши-
ны. Для дальнейшего описания работы колеса введем следующие обозначе-
ния:
v- скорость поступательного движения оси колеса (действительная);
vT - теоретическая скорость;
z
y
v 3
2
1
rcm
P
R
rc
ω
L

rc - свободный радиус колеса – радиус колеса при номинальном давле-
нии воздуха в шине;
rcm - статический радиус колеса – расстояние от оси вращения колеса до
опорной плоскости при номинальной нагрузке на него;
ω - угловая скорость вращения колеса.
Нагрузки, действующие на колесо, разделим на две группы. К первой
группе отнесем силы, действующие на него со сторон рамы и трансмиссии.
Ко второй – нагрузки со стороны опорной поверхности. Нагрузки первой
группы выразим главным вектором Р и главным моментом М, а нагрузки
второй – вектором R и моментом L. При равномерном движении колесо
находится в равновесии под действием этих нагрузок. Основные кинематиче-
ские характеристики движения определяются следующим образом.
Теоретическая скорость движения
vT=ω⋅rc (4.15)
Действительная скорость движения
v=ω⋅rк . (4.16)
Эта скорость определяется также как разность между теоретической
скоростью и потерями скорости, т. е.
v=vT−vn, (4.17)
где vn - потери скорости.
Таким образом
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅= ⋅−= ⋅ − ⋅c
n
к c n c r
v
r rv r
ω ω ω 1ω
, (4.18)
или иначе
⎟⎟= (−ε)
⎠
⎞
⎜⎜
⎝
⎛
=1− T1
T
n
T v v
v
vv , (4.19)
где величину ε называют коэффициентом буксования.
Величина потерь скорости зависит, прежде всего, от силы взаимодей-
ствия между колесом и опорной поверхностью, а также от их физико-
механических свойств.
Из (4.4) и (4.5) имеем также соотношение между радиусом качения и
свободным радиусом
rк=rc(1−ε). (4.20)

Более строго радиус качения определяется посредством, так называе-
мого, радиуса свободного качения. Под этим радиусом понимается радиус
качения колеса в таких условиях, когда продольная составляющая силы вза-
имодействия его с опорной поверхностью равна нулю.
Учитывая зависимость коэффициента буксования от передаваемой ко-
лесом силы тяги величину rк можно рассматривать как кинематическую ха-
рактеристику движения, так и параметр, связывающий скорость движения с
величиной нагрузок, передаваемых колесом. Соотношение между этими
нагрузками определяет режим движения колеса. В общей теории работы ко-
леса выделяют достаточно большое число таких режимов. Для горных машин
основными являются ведущий, ведомый и тормозной. Это обусловлено,
прежде всего, особенностями движения колесных машин в условиях горно-
перерабатывающих предприятий. В соответствии с рис.4.1 ведущий режим
характеризуется тем, что при движении колеса в этом режиме
M0 ; Py0 ; Ry0, (4.21)
в ведомом режиме
M≅0 ; Py0 ; Ry0, (4.22)
а в тормозном режиме
M0 ; Py0 ; Ry0. (4.23)
Особенностью работы колеса является то, что сила Ry является силой
трения, причем ее величина при нормальных условиях работы колеса меньше
предельной силы трения, определяемой законом трения Амонтона-Кулона.
Важно также обратить внимание на т о, что для ведущего колеса равнодей-
ствующая реакций опорной поверхности отклонена от оси колеса в направ-
лении его движения, а для ведомого – наоборот, в противоположную сторо-
ну. При движении колеса в тормозном режиме, независимо от того, ведущее
это колесо или ведомое, полная реакция опорной поверхности отклонена от
его оси в сторону, противоположную движению.
Для движения колеса, как механизма, обладающего двумя степенями
свободы (поступательное и вращательное независимые движения) движущей
силой, обеспечивающей такие движения, является сила трения между коле-
сом и опорной поверхностью. Это ещё раз подчеркивает тот факт, что силы
трения, которые в своем большинстве являются вредными силами сопротив-
ления движению, в некоторых механизмах являются необходимыми. При
равномерном движении колесного движителя по практически недеформиру-
емой опорной поверхности сила Ry равна силе трения. В тех случаях, когда
движение сопровождается большими деформациями несущего основания,
поверхность контакта движителя с опорной поверхностью не является плос-
костью и сила трения распределена по этой сложной по форме поверхности.

4.3.7 Сопротивление движению колесных движителей
Как уже указывалось, при оценке взаимодействия движителей с опор-
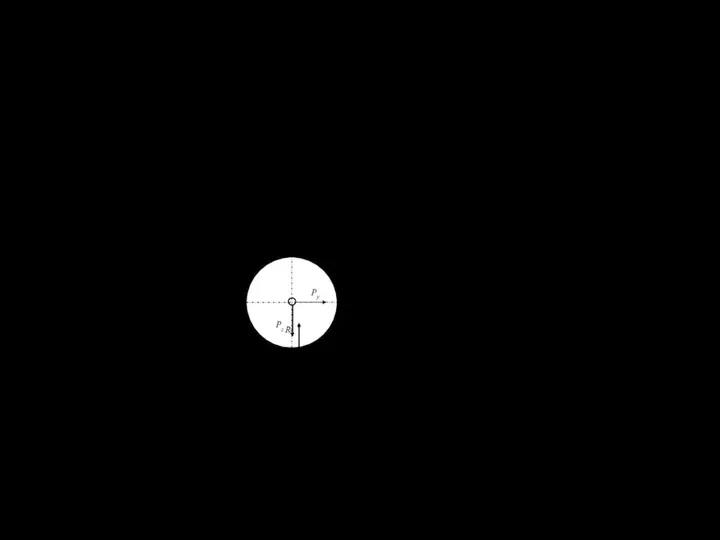
ными основаниями различаются несколько ситуаций в зависимости от их
прочностных характеристик и характера деформаций. При движении колеса
энергия, подводимая к нему от машины, расходуется на деформирование
опорного основания и самого колеса. А также на преодоление трения между
ними и в ступице колеса. При отсутствии буксования эта энергия тратится на
деформирование основания, так как потери энергии в современных ступич-
ных узлах ничтожно малы. В связи с этим сопротивление движению такого
колеса целесообразно оценивать коэффициентом fк, который выражается от-
ношением некоторой толкающей (тянущей) силы Ру для равномерного дви-
жения колеса, нагруженного нормальной к опорной поверхности силой Pz
(Рис.4.5), т. е.
z
y
кP
P
f= . (4.24)
Этот коэффициент может быть определен через плечо сопротивления
качению (снос вертикальной реакции) fк = δ/R.
Рисунок 4.5 – К определению коэффициента сопротивления движению
Так как затраты энергии на движение колеса в основном связаны с де-
формирование его и несущего основания, то коэффициент fк можно предста-
вить в виде суммы
fк=fк′+fк″, (4.25)
где fк′ - выражает потери энергии на деформирование самого колеса;
fк″ - то же на деформирование несущего основания.
v
Py
Pz Rz
Ry δ

Величина коэффициентов fк′ и fк″, а также соотношение между ними
зависит прежде всего от физико-механических свойств колеса и несущего
основания (см. рис4.1). В большинстве случаев значения суммарного коэф-
фициента fк сопротивления движению колеса задаются в справочной литера-
туре [ , ]. Вместе с тем, в некоторых случаях, особенно при создании ма-
шин для работы в нестандартных условиях, величину этих коэффициентов
можно установить расчётным путём.
Взаимодействие жёсткого колеса с жёстким основанием характерно
для железнодорожного транспорта, достаточно широко используемого в гор-
ном производстве. Для такого типа механизмов перемещения характерна не-
значительная величина коэффициента сопротивления качению, составляю-
щая тысячные доли единицы. По справочным данным суммарный коэффици-
ент сопротивления качению железнодорожных колес составляет 0,00 -0,000 .
Рисунок 4.6 – Железнодорожный состав на временных путях,
проложенных на разрабатываемом торфяном месторождении
Наибольшее значение при выборе размеров и числа коле железнодорожных
механизмов перемещения имеют контактные напряжения между колесом и
рельсом. В основу методов расчета этих напряжений положены формулы
Герца, определяющие размеры и фору поверхности соприкосновения при
сжатии двух тел в условиях соблюдения закона Гука. Применительно к
наиболее распространенным рельсам с головкой сложной цилиндрической
формы (Рис.4.4) эти формулы имеют вид

Рисунок 4.6 – Контакт колеса с рельсом:
а) – основные геометрические размеры;
б) – форма пятна контакта и эпюра давлений
3( 2)2
2
max
1
1
π −ν
= ⋅
R
PE
p z ; (4.26)
3
2
2
0 1 2
2
1,55
c
z
ER
P
hhh
⋅
=+= , (4.27)
где E и R - приведенные модули упругости и радиус сжимающихся тел;
1 2
21 2
EE
EE
E
+
⋅
= , (4.28)
1 2
21 2
RR
RR
R
+
⋅
= , (4.29)
h0 – общая деформация рельса и колеса;
h1, h2 - деформация соответственно колеса и рельса.
Радиус колеса и его прочность, должны быть такими, чтобы макси-
мальное напряжение в пятне контакта не превышали допустимые. Допусти-
мые контактные напряжения можно принимать равными твердости материа-
лов по Бриннелю, умноженной на коэффициент запаса. Современные чис-
ленные методы расчёта напряжений и деформаций при контакте колеса с
рельсом [ ] позволяют получить более точные решения, чем по формулам,
приведенным выше. Однако, при предварительных оценках влияния основ-
ных параметров колеса и рельса эти формулы дают более обозримые резуль-
таты.
При движении жесткого колеса по деформируемой опорной поверхно-
сти (Рис.4.5)
2R1
R2
Pz
б)
а)
pmax

Рисунок 4.7 – Взаимодействие жесткого колеса
с деформируемым основанием
Жесткие колеса применяются в качестве элементов опорно-ходовых
устройств достаточно редко, например, ходовые устройства в некоторых до-
рожных и торфяных машинах. Изучению взаимодействия таких коле с де-
формируемыми грунтами посвящено большое количество исследований [ , ].
Здесь приведем некоторые расчётные зависимости, которые справедливы при
давлениях между колесом и опорным основанием до 40 кПа [ ]. В таких
условиях коэффициент сопротивления движению ведомого колеса
ω
Py
v
y
z
R1
h2
a’ a
b
Pz
h2’

∫
∫∫
==
s
н z
s
н y
z
y
к pdS
pdS
P
P
f , (4.30)
где рн - нормальное давление между колесом и грунтом;
dSy, dSz - проекции элементов площади контакта на плоскости, перпен-
дикулярные Оy и Оz.
Воспользовавшись величиной среднего давления и вынеся его за знак
интеграла, получим
∫
∫∫
=
s
z
s
y
к dS
dS
f . (4.31)
Так как ∫dS=b(h2−h2′)
s
y , а ∫dS=b(a+a′)
s
z ,
то
aa
hh
fк
+′
− ′
=2 2, (4.32)
где h2, h2′ - полная и остаточная деформация несущего основания;
a, a′ - длины передней и задней относительно оси частей контакта.
В большинстве реальных условий работы колес величины h2′ и a′ малы
по сравнению с h2 и a. Кроме того, восстановление геометрии несущего ос-
нования происходит спустя некоторое время после прохода колеса, поэтому
задняя часть контакта колеса с грунтом оказывает незначительное влияние на
условия равновесия с колесом. В связи с этим, величинами h2′ и a′ в формуле
(4.32) можно пренебречь. Тогда с небольшим увеличением значения fк можно
приблизительно вычислить по приближенной формуле
a
h
fк≅2, (4.33)
Так как (Рис.4.5)
a=R12−(R1−h2)2=2R1⋅h2−h22, (4.34)
то, пренебрегая квадратом значения h2, имеем
1
2
12
2
2 2R
h
Rh
h
fк ≅
⋅
≅ , (4.35)

Учитывая, что (4.35) дает несколько завышенные значения fк целесооб-
разно это учитывать поправочным коэффициентом kf и пользоваться выра-
жением
1
2
2R
h
fк=kf , (4.36)
где kf=0,6÷0,9 (его меньшие значения соответствуют менее жестким коле-
сам).
Формула (4.36) может также использоваться и для определения коэф-
фициента сопротивления качению пневматических колес по деформируемым
опорным основаниям в тех случаях, когда деформации колес намного мень-
ше, чем деформации несущих оснований. Обычно это имеет место при зна-
чительных внутренних давлениях в шинах. Большинство колесных пневма-
тических движителей горных машин удовлетворяют этому условию. Исклю-
чение составляют лишь колесные движители высокой проходимости с не-
большим внутренним давлением в шинах (меньше 20 кПа).
В таких ситуациях имеет место значительное деформирование, как не-
сущего основания, так и самого колеса. Для определения деформации пнев-
матического колеса под нормальной к несущей поверхности нагрузкой ис-
пользуется несколько зависимостей [ ]. Самая простая из них линейная, со-
гласно которой
z
z
C
P
h1= , (4.37)
где Сz - радиальная жесткость колеса (шины).
Значение Cz зависит от давления в шине и её конструкций. Ориентиро-
вочно в первом приближении её можно определить для нормальных условий
работы шин используя справочные данные каталогов заводов-изготовителей
c ст
zn
z r r
P
C
≅−
(4.38)
где Pzn - номинальная грузоподъемность шины;
rc, rст - соответственно свободный и статический её радиусы.
Значения Pzn, rc, rст, обычно приводятся в технических данных шин.
Деформации несущего основания (дороги) зависят как от его физико-
механических характеристик, так и от размеров и формы пятна контакта, ве-
личины нормальных напряжений между колесом и опорной поверхностью, а
также и от давления в шине. (Рис. 4.8).

Рисунок 4.8 – Взаимодействие пневматического колеса
с деформируемым несущим основанием
Максимальная нормальная деформация несущего основания может в
этом случае вычисляться по формуле [ ]
( )
m pвrc
h E ⋅
−
=
2
2
2
2
21ν
. (4.39)
где рв - давление воздуха в шине.
rcт
h2
O
pк pк

Эта формула предложена проф. Ф.А. Опейко [ ] для определения де-
формаций торфяных залежей под колесными машинами на пневматических
шинах. Средняя деформация несущего основания при этом принимается рав-
ной двум третьим от максимальной, т. е.
( )
m pвrc
h h E ⋅
−
= =
2
2
2
2 2
1
3
4
3
2 ν
. (4.40)
Приведенные зависимости получены на основании решений контакт-
ных задач теории упругости, полученных Герцем [ ]. Реальные несущие ос-
нования, по которым перемещаются горные машины, различаются по своим
физико-механическим свойствам как качественно, так и количественно. Это
не позволяет охватить все возможные ситуации взаимодействия колеса с не-
сущим основанием единой функциональной зависимостью. Поэтому суще-
ствует много подобного типа зависимостей [ , , ], которые в конкретных
ситуациях дают более точные результаты. Более того, задача исчисления
напряжений и деформаций в контакте колеса с несущим основанием реали-
зована в ряде инженерных программных сред [ ]. Вместе с тем, следует учи-
тывать, что более сложные функциональные зависимости требуют большего
числа физико-механических характеристик колеса и опорного основания, а
численные способы исследования их взаимодействия сопряжены с большим
объемом вычислений и обусловленной этим возрастанием погрешности ре-
зультата. С целью оценки влияния основных характеристик пневматического
колеса и несущего основания на величину деформации последнего в [ ]
предлагается формула
4
3
2 2
1
c
z z
r
PC
E b
h ⋅
⋅
=
π
, (4.41)
где b=B2 - ширина профиля шины.
4.3.8 Ядро сечения колесного движителя
Вертикальные нагрузки на каждое колесо движителя определяют
обычно из условий равновесия или уравнений движения машины. При этом
используют и различные другие условия, например, совместность деформа-
ций шин и т.п.
Для простейшего двухосного колесного движителя (Рис. 4.9) нормаль-
ные к опорной поверхности нагрузки находятся из уравнений равновесия
машины в вертикальной плоскости.

Рис. 4.9 - Расчетная схема двухосной машины
Эти условия записываются в виде
∑
=
=
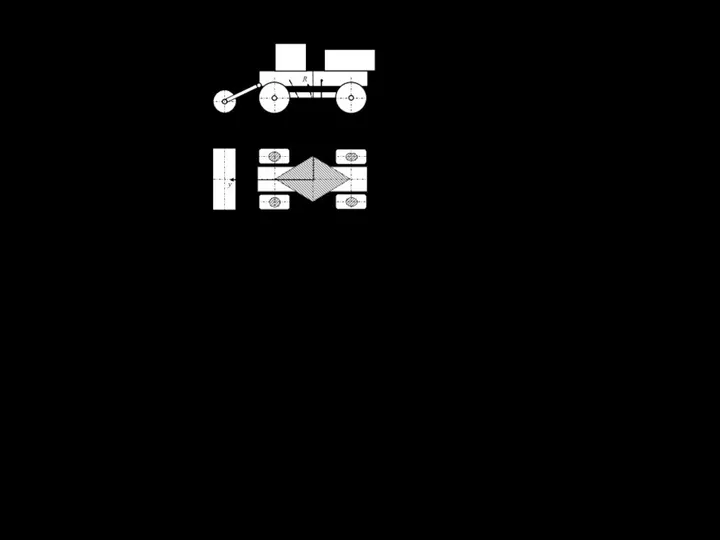
n
i
PziRz
1
,
∑ ( )
=
= ⋅
n
i
MyPziRzxд
1
0 , (4.42)
∑ ( )
=
= ⋅
n
i
MxPziRzyд
1
0 ,
где n – число колес ходового устройства машины;
Pzi – нормальная к опорной поверхности нагрузка на i-е колесо;
Rz – общая реакция опорной поверхности на машину (равнодействую-
щая всех нормальных реакций колес);
xд, yд – координаты центра давления;
MOy(Pzi), MOx(Pzi) – моменты внешних сил относительно осей Ox и Oy.
Конкретный вид этих уравнений зависит от конструкции ходового устрой-
ства, подвески колес, вида рабочего оборудования и ряда других факторов,
характер действия которых обычно учитывается в дополнительных уравне-
ниях к системе (4.42).
Работа колесного движителя существенно зависит от распределения
нагрузок по колесам, т. е. от положения центра давления.
На машину действует сила тяжести, нагрузки со стороны разрабатыва-
емой породы Р и реакции опорной поверхности на колеса. Под действием
этих сил она находится в равновесии. Для нормальной работы ходового
устройства необходимо, чтобы все колеса передавали нагрузку на опорную
mq
а
x
y
a
d
z
Р
R

поверхность. Выполнение этого условия обеспечивается тогда, когда центр
давления находится в пределах ядра сечения опорной поверхности. Размеры
и форма ядра сечения, в основном зависит от типа колес (жесткие, упругие) и
подвески. Для определения его формы и размеров определим экстремальные
значения давления по формуле (1.17)
y
y
x
z x
W
M
W
M
S
P
p= ± ±
0
0
min
max , (4.43)
где Pz0 – общая нормальная к опорной поверхности нагрузка машины на
опорное основание;
S0 – суммарная площадь контакта колес с опорной поверхностью;
Mx , My – моменты внешних сил относительно соответствующих осей;
Wx , Wy – моменты сопротивления опорной площади относительно тех же
осей.
Для равных по площади контактных площадок двухосной машины
S0=4⋅Sк, (4.44)
где Sк – площадь контакта одного колеса.
Моменты сопротивления опорной площади движителя
ymax
I
Wx= x,
xmax
I
Wy= y, (4.45)
где Ix , Iy – моменты инерции опорной площади относительно соответству-
ющих осей;
xmax , ymax – максимальные значения координат контактных площадок.
Моменты инерции, учитывая малость контактных площадок колес по
сравнению с общими размерами опорной площади ходового устройства, вы-
числяем по упрощенным формулам
4 4
а2
Ix= ⋅Sк⋅ ;
4 4
d2
Iy= ⋅Sк⋅ . (4.46)
Примем ymax=a2, xmax=d2. Тогда
Wx=2⋅a⋅Sк; Wy=2⋅d⋅Sк. (4.47)
Учитывая, что Mx=Pz0⋅yд, My=Pz0⋅xд и подставив эти значения,
а также значения Wx и Wy в (5) и принимая во внимание то, что на границе
ядра сечения pmin=0, имеем

к
z дм
к
z дм
к
z
dS
Px
аS
Py
S
P
⋅ ⋅
⋅
−
⋅ ⋅
⋅
−
0=4⋅ 2 2
0 0 0 (4.48)
или
d
x
а
yдм−дм
=−
2
1
0 , (4.49)
где хдм , удм – координаты границ ядра сечения.
Соотношение (4.49) указывает на то, что контур ядра сечения колесной
двухосной машины на жестких колесах ограничен прямыми линиями. Ядро
сечения представляет собой ромб с диагоналями, равными d и a (см. рис.
4.9). Максимальные значения границ ядра сечения
xд.max=±d2, yд.max=±a2. (4.50)
Таким же образом определяем размеры ядра сечения трехосного и че-
тырехосного хода (рис.4, а,б). Колесные машины на пневматических шинах и
с упругой подвеской колес имеют ядро сечения другой формы и больших
размеров. Поэтому допустимое положение центра давления для жестких ко-
лесных машин тем более допустимо для машин на пневматических шинах с
упругой подвеской колес.
Применяя формулу (4.43) для трехосной и четырехосной машин с
жесткими колесами и повторяя последовательность определения размеров
ядра сечения двухосной машины, имеем:
– для трехосной машины
Ix=a ⋅4⋅Sк
4
2
; Iy=d ⋅6⋅Sк
4
2
;
(4.51)
Wx=2⋅a⋅Sк; Wy=3⋅d⋅Sк
условие равенства нулю минимального значения р
к
z дм
к
z дм
к
z
dS
Px
aS
Py
S
P
⋅ ⋅
⋅
±
⋅ ⋅
⋅
±
0=6⋅ 2 3
0 0 0
или
d
x
a
yдм дм
⋅
⋅
= +
3
2
3
1 , (4.52)
откуда
xдmax=±d2; yдmax=±a3. (4.53)

Рис. 4.10 - Ядра сечения трехосной (а) и четырехосной (б) машин
– для четырехосной машины
Ix aSк aSкaSк ⎟= ⋅a⋅Sк
⎠
⎞
⎜
⎝
= ⋅4⋅+ ⋅2⋅=2⋅ ⋅⎛+ 2
4
5
4
1
1
44 416
;
Wx= ⋅a⋅Sк
2
5 ;
Iy= ⋅d ⋅Sк= ⋅d2⋅Sк
2
2
84
;
Wy=4⋅d⋅Sк.
к
z дм
к
z дм
к
z
dS
Px
aS
Py
S
P
⋅ ⋅
⋅
±
⋅ ⋅
⋅ ⋅
±
= ⋅ 5 4
2
08
0 0 0 ,
xдmax=±d2; yд а
16
max=±5 . (4.54)
Представляет практический интерес определение размеров ядра сече-
ния колесного хода с шарнирным соединением переднего моста с рамой, зад-
ний мост к которой крепится жестко (рис. 5). Так как для колесного хода
условие pmin=0 равносильно условию равенства нулю нагрузки на одно из
колес, то для определения размеров ядра сечения определим зависимость ре-
акций опорной поверхности на все колеса от координат центра давления.
d
а
а/3
x
y
а
d
а
a
16
5
x
б y

Суммарные реакции на колеса переднего и заднего мостов
a
y
Rп=Pz0⋅д;
a
ay
Rз=Pz0⋅−д, (4.55)
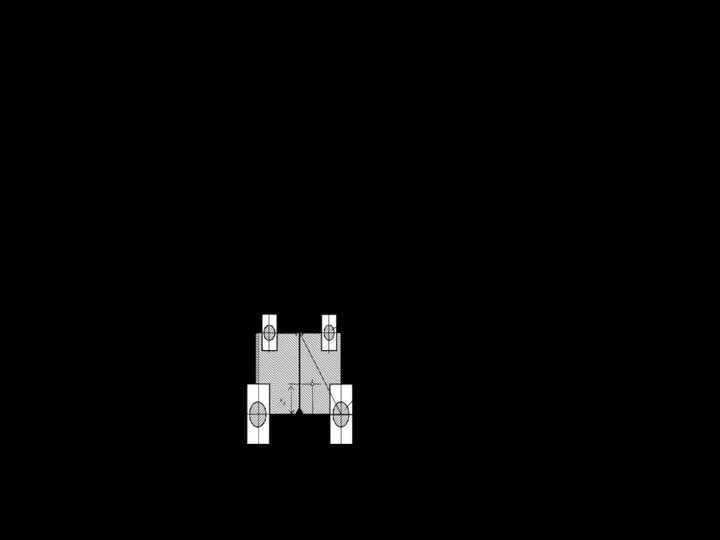
где Rп=Rпл+Rпп – общая реакция грунта на передний мост;
Rз=Rзл+Rзп – то же на задний мост;
Rпл, Rзл, Rпп, Rзп, – реакции опорного основания на колеса левого и право-
го бортов соответственно переднего и заднего мостов.
а
y
RплRппPz д
= =0⋅2⋅
; (4.56)
⎟
⎠
⎞
⎜
⎝
зл=z⋅−д⋅⎛d−xд
a
ay
RP0 22 ;
(4.57)
⎟
⎠
⎞
⎜
⎝
зп=z⋅−д⋅⎛d+xд
a
ay
RP0 22 .
Приравняв к нулю эти реакции, убеждаемся, что ядро сечения такого
хода – прямоугольник со сторонами d2 и а, т. е. максимально возможные ко-
ординаты центра давления для такого колесного хода
xдmax=±d2; yдmin=0; yдmax=а. (4.58)
Рис. 4.11 - К определению размеров ядра сечения
двухосного колесного движителя с шарнирным соединением
переднего моста и рамы
а
d2
d1
x
y
Sк1
Sк2
уд
хд

Определим размеры пятна контакта колеса, считая, что величины Pzi
определены.
Площадь пятна контакта колеса с опорным основанием зависит от его
конструкции и величины нормальной нагрузки Pzi . Форма пятна контакта
также весьма различна и может меняться от круга до прямоугольника. Чаще
всего пятно контакта имеет форму овала и его площадь может быть опреде-
лена по формуле
Sк=π⋅a⋅b, (4.59)
где a и b - полуоси элипcа (реально это половины длины и ширины пятна
контакта). Для практических расчетов размер b принимается равным поло-
вине ширины беговой дорожки шины, а размер а вычисляется по формуле
a=rc2−(rc−hк)2, (4.60)
где rc – свободный радиус колеса;
hк – деформация шины.
Деформацию hк шины можно вычислить, используя выражение
hк=Pzcz, (4.61)
где сz - радиальная жесткость шины.
Значения радиальной жесткости шин зависит от типа и размеров шины,
а также внутреннего давления воздуха. При номинальном давлении радиаль-
ная жесткость может быть найдена из справочных данных каталогов заводов-
изготовителей шин, где обычно указываются номинальная грузоподъем-
ность, давление воздуха в шине, свободный и статический радиусы. В этом
случае радиальная жесткость
c cт
zп
z rr
P
c
=−
, (4.62)
где rc – свободный радиус шины;
rcт – статический радиус при нормальной нагрузке;
Рzn – номинальная грузоподъемность.
Определив давление колес на опорную поверхность p=PzSк можно
проверить возможность эксплуатации движителя в конкретных условиях.
Чаще всего это делается сопоставлением расчетных давлений с допустимы-
ми. На дорогах с твердым покрытием это требование обычно выражается до-
пускаемой нагрузкой на ось.

4.3.9 Мощность для передвижения колесного движителя
Необходимая для передвижения горной машины на колесном ходу
мощность вычисляется по формуле
1000η
PTvT
N= ⋅ , (4.63)
где РТ - суммарные тяговые усилие ведущих колес движителя;
vT - теоретическая скорость движения;
η - КПД привода ведущих колес;
1000 – переводной коэффициент для получения результата вычислений в
кВт.
Этот коэффициент будем использовать во всех случаях вычисления
мощности, так как почти все механизмы в горных машинах потребляют
мощности, величина которых составляет десятки, сотни и тысячи кВт, а вхо-
дящие в формулу величины измеряются в системе СИ.
Суммарное тяговое усилие ведущих колес машины должно быть не
меньшим, чем общая сила сопротивления движению, т.е.
∑
=
=
n
i
PT Pi
1
, (4.64)
где Рi - отдельные составляющие общей силы сопротивления движению;
п - число составляющих сопротивлений движению.
Это число зависит от конкретных условий движения машины. Для гор-
ных машин, скорости движения которых, как правило, невелики, а пути пе-
ремещения расположены вне стационарной сети дорог, чаще всего необхо-
димо учитывать следующие силы:
P1=Pz0⋅fк - сила сопротивления деформированию несущего основания
и колес;
P2=m⋅g⋅sinϕ - составляющая силы тяжести, параллельная опорной по-
верхности, и возникающая при движении машины в гору (Рис.4.12);
m - масса машины;
φ - угол наклона опорной поверхности к горизонту.
Р3 – сила сопротивления, возникающая вследствие рабочих органов
машины с горной породой (сопротивление подаче, крюковое усилие и т.п.);
tp
v
Cm
dt
dv
P4=C⋅m≅ ⋅ - сила инерции, возникающая при разгоне машины,
где С – коэффициент, учитывающий разгон вращающихся масс;
t - время разгона.

Рисунок 4.12 – Определение составляющей силы тяжести,
параллельной опорной поверхности
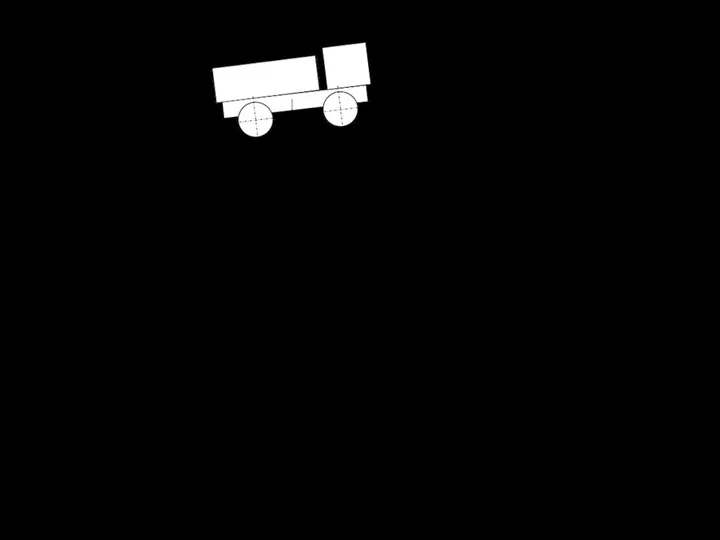
4.3.10 Условия возможности передвижения машины
на колесном движителе
Мобильные горные машины на колесном ходу работают в самых раз-
личных условиях. На возможности их передвижения могут оказывать влия-
ние всевозможные ограничения: габаритные, маневренные, водные, тягово-
сцепные и т.п. в реальных ситуациях передвижения машин их остановки как
следствие невозможности передвижения происходят по двум основным при-
чинам: недостаток мощности или буксование ведущих колес. Такие останов-
ки бывают при не выполнении двух основных условий возможности пере-
движения: достаточности мощности и сцепления.
Первое из этих условий выражается соотношением
1000η
TT
д
Pv
NN= ⋅ , (4.64)
где Nд – мощность, передаваемая от энергетических установок на ведущие
колеса.
Второе условие заключается в отсутствии полного буксования ведущих
колес, которое наступает при превышении необходимого суммарного тягово-
го усилии предельной силы сцепления ведущих колес с несущим основани-
ем. Выражение можно записать в виде
zв c
p
z к P f
t
v
P0⋅f+m⋅g⋅sinϕ+P3+C⋅m ⋅ , (4.65)
где Рzв – нормальная к опорной поверхности нагрузка, передаваемая веду-
щими колесами (сцепной вес);
fс - коэффициент сцепления между движителем и несущим основанием.
m·g
φ

Эти условия передвижения далеко не единственные, но, как правило,
они должны соблюдаться во всех случаях. Представляет некоторый интерес
ситуация, когда машина на колесном движителе перемещается на горизон-
тальной опорной поверхности равномерно при отсутствии силы Р3. В этом
случае Pzв=m⋅g, и условие достаточности сцепления принимает вид
mg
P
c fк zв
⋅
ϕ≥″ , (4.66)
а при полноприводном движителе, когда Pzв=m⋅g
ϕc≥fк″⋅k. (4.67)
При определении мощности для передвижения железнодорожного ко-
лесного движителя, где коэффициент fк очень мал (менее 0,01), необходимо
учитывать и сопротивление в подшипниках колесных пар,, т. е. при опреде-
лении необходимого тягового усилия составляющая Р1 вычисляется по фор-
муле
P1=(fк+fn)Pz0, (4.68)
где fn – коэффициент сопротивления в подшипниках колесных пар.
При определении силы сопротивления качению в обычных колесных
движителях коэффициент fn не учитывается ввиду его малости по сравнению
с коэффициентом fк.
4.3.11 Системы поворота колесных движителей
Горные мобильные машины, как правило, в процессе движения совер-
шают маневры. При этом габариты пространства, в котором они перемеща-
ются, ограничены. Поэтому к механизмам их перемещения предъявляются
довольно жёсткие маневренные требования. Маневренные качества колесных
движителей оцениваются, в первую очередь, угловой скоростью и радиусом
поворота, а также габаритами полосы движения. В горных машинах на ко-
лёсном ходу используются системы поворота, которые можно классифици-
ровать по принципам изменения направления движения. В этом смысле раз-
личают системы поворота (Рис. 4.12) за счёт:
- поворота колес одной или нескольких осей;
- поворота одной или нескольких осей, а также поворота полурам;
- разности скоростей вращения колес противоположных бортов.
Если используется первая система поворота (на рис. 4.13,а представлен
её самый простой вариант), то радиус и угловая скорость поворота определя-
ется соотношениями
ω tgα
a
=v ;
tgα
a
R= , (4.69)

где v – продольная составляющая скорости точки машины, лежащей на её
продольной оси;
α – средний угол поворота управляемых колёс передней оси.
Колёсные машины с поворотными осями (Рис.4.13,б) используются го-
раздо реже по причине невысокой динамической устойчивости. Радиус и уг-
ловая скорость простейшего варианта такой системы определяется формула-
ми (4.69), в которых угол α есть угол поворота оси относительно поперечной
оси машины.
Схема поворота за счёт складывания полурам (Рис.4.13,в) используется
в горных машинах сравнительно часто. Особенно это относится к погрузоч-
но-доставочным машинам, как при открытой добыче, так и при подземных
разработках месторождений полезных ископаемых. Радиус и угловая ско-
рость поворота при симметричном относительно шарнира вкладывания по-
лурам осей мостов, определяются выражениями
2sin2
β
a
R= ,
(4.70)
2sin2
β
ω
a
=v ,
где v – продольная скорость мостов;
а = а1 + а2 – продольная база машины;
β – угол складывания полурам.
При использовании бортовой схемы управления поворотом радиус и
угловая скорость соответственно
2ω
v1v2
R=+ ;
(4.71)
d
ω=v2−v1,
где v2=ω2⋅rк2, v1=ω1⋅rк1 - продольные составляющие скоростей середин
бортов;
ω1, ω2 – угловые скорости вращения колёс левого (отстающего) и пра-
вого (забегающего) бортов;
rк1, rк2 - радиусы качения колёс левого и правого бортов.
При совершении маневров колёсные движители тратят дополнительную
мощность на их совершение. Эти дополнительные затраты зависят как от ра-
диуса совершаемого поворота, так и системы управления поворотом.

Рисунок 4.13 – Основные системы поворота колесных машин:
а) – за счёт поворота колес; б) – за счёт поворота оси;
в) – все колеса управляемые («краб»); г) – за счёт складывания полурам;
д) – комбинированная схема; е) – бортовой поворот
а
R d
v
C
а)
R d
C
е)
а
v2
v1
а1
R d
v
C
г)
а2
β
а
v
R d
C
б)
β
а
R d
v
C
в)
а
R d
v
C
д)
β1
β2
+β
-β
β

Рисунок 4.14 - Вагон самоходный 5ВС15М (схема «краб»)
Рисунок 4.15 - Самоходный вагон В15К (схема 6х3)

4.4 Гусеничные движители
4.4.1 Принципиальные схемы и принцип действия
В горных мобильных машинах гусеничные движители – самый распро-
страненный механизм перемещения. Зачастую подачу органов разрушения
массива породы также осуществляют с помощью этого механизма. Его прин-
ципиальная схема приведена на рис.4.14.
Рисунок 4.14 – Принципиальная схема гусеничного движителя:
1 – рама; 2 – гусеничная цепь; 3 – ведущая звездочка;
4- натяжное колесо; 5 – опорные катки; 6 – поддерживающие ролики
Широкое распространение гусеничных движителей в качестве опорно-
ходовых устройств горных машин обусловлено их хорошими тягово-
сцепными и маневренными качествами, а также высокой проходимостью по
опорным основаниям с малой несущей способностью. Гусеничные движите-
ли различаются и классифицируются по нескольким признакам и делятся на
активные и пассивные: одноопорые и двухопорные; с жесткой и балансирной
упругой подвеской опорных катков; с передним и задним расположением ве-
дущих звездочек; с планетарным и дифференциальным механизмами поворо-
та и т.д.
При изучении гусеничных движителей будем опираться на теоретиче-
ские основы работы таких движителей, разработанные в БНТУ проф. Ф.А.
Опейко [4.1] и нашедшие применение в решении различных прикладных за-
дач, особенно, связанных с поворотом таких движителей.
4.4.2 Основные математические соотношения
Перемещение движителя осуществляется за счет перематывания гусе-
ничных цепей относительно рамы. При этом различают действительную и
теоретическую скорости движения, которые, как и для колесного движителя,
связаны соотношением
v=vT(1−ε). (4.72)
v
ω
6 2 4
3 5 1

Теоретическая скорость vT равна скорости перематывания гусеничных
цепей
vT=u,
где u=ωзв⋅rзв;
ωзв – угловая скорость ведущей звездочки;
rзв – делительный радиус ведущей звездочки.
При отсутствии буксования движителя действительная скорость совпа-
дает с теоретической. В действительности буксование присутствует всегда,
но при движении по жестким опорным основаниям без каких-либо значи-
тельных внешних нагрузок величина буксования очень мала и им можно
пренебречь при рассмотрении кинематики. Однако в соответствии с выводом
раздела 4.2 величина буксования в значительной степени определяет силу
трения между гусеницей и опорной поверхностью. Взаимодействие между
гусеницами опорной поверхностью характеризуется еще рядом силовых па-
раметров, среди которых наиболее часто используются такие, как среднее и
экстремальные значения нормальных давлений, тяговые усилия гусеничных
лент, силы сопротивления движению и т.п.
4.4.3 Мощность для передвижения гусеничного движителя
Для определения мощности и условий возможности движения машины
на гусеничном движителе необходимо знать тяговые усилия гусеничных
лент, так как мощность для прямолинейного передвижения машины, приве-
денная к энергетической установке, выражаемая в кВт, и определяется по
формуле
⋅η
⋅
=
1000
TTvT
N , (4.73)
где TT - суммарное тяговое усилие гусеничных лент;
vT - теоретическая скорость передвижения;
η - КПД привода гусеничного движителя.
Тяговые усилия гусеничных лент
Суммарное тяговое усилие гусеничных лент должно уравновешивать
все силы сопротивления движению, т.е.
=∑
n
TT Pi
1
, (4.74)
где п – число сил сопротивления движению;
Pi – i-я сила сопротивления движению.
Среди этих сил чаще всего выделяют следующие:
сила сопротивления движению опорного основания;
P1=2fд⋅p⋅a⋅b, (4.74)

где fд – коэффициент сопротивления деформированию несущего основания.
Этот коэффициент в свое время проф. Ф.А. Опейко называл коэффициентом
сопротивления мятию грунта и представил его суммой двух составляющих fд’
и fд’’, которые отражают сложный характер деформации несущего основания
между опорными катками;
ab
P
p z
=2⋅
- среднее давление гусениц на опорное основание;
Рz – проекция на нормаль к опорной поверхности равнодействующей
внешних сил, действующих на машину;
a, b – размеры опорной площадки гусеницы.
P2=2fк⋅p⋅a⋅b - сила сопротивления, обусловленная внутренними по-
терями в гусеничном обводе;
fк - коэффициент сопротивления, учитывающий внутренние потери в
гусеничном обводе, прежде всего, сопротивление качению опорных катков
по гусеничным лентам;
Р3 - сила сопротивления движению, вызванная взаимодействием рабо-
чих органов с массивом горной породы, а также сопротивлением движению
прицепных машин;
P4=K′⋅Tб - сила сопротивления движению, вызванная трением опор-
ных катков о направляющие гусеничных лент.
Тб – боковая сила, действующая на машину, например сила ветра или
составляющая сил тяжести при работе машины на косогоре.
dt
dv
P5=c⋅m - составляющая силы сопротивления, необходимая для раз-
гона машины при её трогании;
с – коэффициент, учитывающий разгон вращающихся масс привода гу-
сеничного движителя (можно принимать равным 1,01…1,05).
m – масса машины;
dt
dv - ускорение машины при ее разгоне; это ускорение можно вычис-
лить по упрощенной формуле
p
p
t
v
dt
dv≅ , (4.75)
где tp – время разгона машины;
P6=m⋅g⋅cosϕ - сила сопротивления, вызванная составляющей силы
тяжести, параллельной опорной поверхности;
φ – угол наклона опорной поверхности.
Кроме этих сил могут действовать и другие силы, например, сила ветра
и т.п.
Таким образом, чтобы определить мощность для передвижения горной
гусеничной машины по прямой надо знать значения ряда коэффициентов,
часть которых можно найти в справочной литературе [ ], а часть можно
определить и расчетным путем.

4.4.3 Коэффициент сопротивления деформации несущего основания
Так, например, коэффициент fд сопротивления деформированию опор-
ного основания зависит от прочностных свойств и величины его деформации.
Для его определения рассмотрим работу, затрачиваемую гусеницей на де-
формирование грунта при ее перемещении на расстояние l (Рис.4.15).
Рисунок 4.15 – К определению коэффициента
сопротивления деформированию грунта
Работа этой силы
A=P1⋅l. (4.77)
С другой стороны, работу, затраченную на деформирование грунта,
можно выразить как
i
l n
i
A=∫p⋅dV=p⋅b⋅l⋅h+∑pi⋅ i⋅l⋅b
0 =1
λ , (4.78)
где
ab
P
p z
= ⋅
- среднее давление гусеницы на опорное основание;
Pz – нормальная к опорной поверхности нагрузка, передаваемая гусени-
цей на опорное основание;
pi – давление под опорными катками;
λi – стрела провеса гусеничной ленты между соответствующими опорны-
ми катками.
Так как коэффициент сопротивления деформированию несущего осно-
вания представляет собой отношение
z
дP
P
f=1, (4.79)
то, приравняв 4. и 4. и учитывая, что Pz=p⋅a⋅b, имеем
pa
p
a
h
f
z
i i
д ⋅
⋅
=+
∑
−1
1
λ
. (4.80)
Приравняв pi = p и Σλi = (z - 1), запишем
h
λ
Pz Px v

( )
a
z
a
h
fд=+−1λ, (4.80)
где z – число опорных катков;
λ – среднее значение стрелы провеса гусеничной ленты между опорными
катками.
Формула 4.00 указывает на влияние числа опорных катков на величину
коэффициента сопротивления деформированию грунта. В реальных машинах
второй член в (4.80) намного меньше первого, поэтому в предварительных
расчетах можно принимать
a
h
fд≅ , (4.81)
Остальные коэффициенты, входящие в расчетные формулы для опре-
деления сил сопротивления движению гусеничного движителя, чаще всего
определяются по результатам специальных экспериментов и приводятся в
специальной литературе [ ].
Коэффициент сопротивления деформированию несущего основания
удобно представить в виде суммы двух составляющих, первая из которых
выражает силу сопротивления из-за действия внешних сил, а вторая отражает
внутренние силы, т.е. горизонтальные напряжения в опорном основании. Та-
ким образом, можно записать
fд=fд′+fд″, (4.82)
где fд′ и fд″ - составляющие коэффициента fд.
Для выяснения физического смысла коэффициентов fд′ и fд″, рассмот-
рим напряженное состояние несущего основания в промежутке между двумя
соседними опорными катками гусеницы пассивного движителя.
Рисунок 4.16 – К влиянию составляющих fд′ и fд″ коэффициента fд.
Рассматривая две симметричные относительно середины пролета точки
и считая, что в этих точках на гусеницу со стороны несущего основания дей-
ствуют равные напряжения, запишем
∫≅
f
σzPz; ∫≅
f
σy0
σу σу
σz σz
σ σ

где σz и σу – проекции напряжения, действующего на гусеницу;
Pz - нормальная к опорной поверхности нагрузка, действующая на опор-
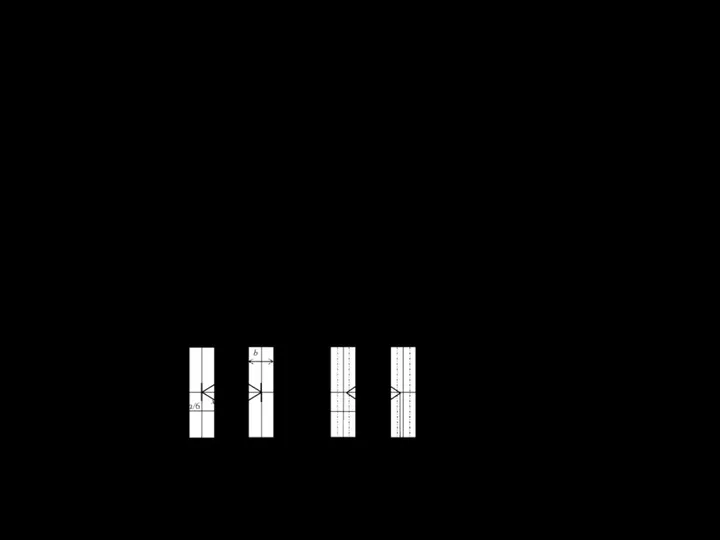
ное основание со стороны гусеницы.
Однако энергия, подводимая к гусенице, тратится на преодоление всех
напряжений. Поэтому представление fд в виде суммы двух составляющих
отражает различный характер сил сопротивления деформации несущего ос-
нования.
4.4.4 Распределение давления на несущее основание
и его деформации
Давление, которое оказывает гусеничный движитель на несущее осно-
вание, является его весьма важной характеристикой и, зачастую. Определяет
область его применения. Величина давления зависит как от конструктивных
размеров гусеничного движителя, массы машины и других нагрузок, дей-
ствующих на машину. Среднее давление гусеничного движителя на несущее
основание
ab
F
p z
=2⋅
, (4.84)
где Fz – проекция равнодействующей всех внешних сил на ось, перпендику-
лярную опорной поверхности.
Максимальные и минимальные давления определяют по формулам
(1.17). Входящие в эти формулы моменты сопротивления опорной поверхно-
сти зависят от конструктивных особенностей движителя: типа подвески
опорных катков, их числа, способа соединения гусениц с рамой машины.
Рассмотрим наиболее распространенные жесткие одно- и двухопорные гусе-
ничные движители.
Рисунок 4.17 – Ядро сечения основных типов гусеничных движителей:
а) - одноопорный движитель; б) - двухопорный движитель
d
y
x
a
b
a/6 a/6 x
y
(db)
b d
+
+
6
332

Для жесткого одноопорного движителя моменты сопротивления опор-
ной площади с учетом того, что давление по ширине гусениц не меняется,
определяются по формулам
( ) ( )
12 /2 3
3 2 2
max
ab
a
dba dba
y
I
Wx x = ⋅
−
+ −−
= = ;
(4.85)
abd
d
d
ab
x
I
Wy y = ⋅⋅
⋅
= =
/2
2 4
2
max
;
где Ix и Iy - моменты инерции опорной площади относительно соответству-
ющих осей;
ymax = a/2, xmax = d/2 - максимальные координаты точек опорной площади.
Mx=Fz⋅yд;
(4.86)
My=Fz⋅xд,
где хд, уд - координаты центра давления.
Имеем
⎟
⎠
⎞
⎜
⎝
=⎛+ +
⋅⋅
⋅
+
⋅
⋅
+
= ⋅ d
x
a
y
p
abd
Fx
ab
Fy
ab
F
p z 3z д zд 16д2д
max2 2
,
(4.87)
⎟
⎠
⎞
⎜
⎝
=⎛− −
⋅⋅
⋅
−
⋅
⋅
−
= ⋅ d
x
a
y
p
abd
Fx
ab
Fy
ab
F
p z 3z д zд 16д2д
min2 2
.
Приравняв к нулю последнее выражение, получим уравнение линии,
охватывающей ядро сечения жесткого одноопорного гусеничного хода
1−60−20=0
d
x
a
yд д . (4.88)
где хд0, уд0 - координаты границы ядра сечения.
Это уравнение указывает на то, что ядро сечения ограничено прямыми
линиям и представляет собой ромб с координатами вершин
max 2
d
xд=± ,
max 6
a
yд=± (Рис.4.17). При этом ядро сечения включает, как указывает проф.
Ф.А. Опейко, два отрезка прямых длиной
3
a на осях гусениц.

У двухопорного жесткого гусеничного движителя давление изменяется
как по длине, так и по ширине гусениц, а моменты сопротивления опорной
площади (см.рис.4.17) равны
( ) ( )
12/2 3
3 3 2
max
ab
a
dba dba
y
I
Wx= x=− −− = ⋅;
(4.89)
[( ) ( )]
( )
( )
(db)
ab d
db
adb db
x
I
Wy y
+
+
=
+
+−−
= =
3
3
12 /2
3 3 62 2
max
.
Воспользовавшись теперь формулами (1.17) и учитывая (4.89), запи-
шем условие равенства нулю минимального значения давления
( )
ab(b d)
Fxdb
ab
Fy
ab
Fz z д zд
3
3 3
02 2 ⋅ 2+
⋅ +
−
⋅
⋅
−
= ⋅
,
(4.90)
или
( )
232
3 3
2
1
0
b d
xdb
a
yд д
+
+
=− − .
Из этого соотношения заключаем, что контур ядра сечения ограничен
прямыми линиями и его точки на осях Ох и Оу, т. е. принимая попеременно
хд = 0 и уд = 0, убеждаемся, что ядро сечения – ромб с вершинами на этих
осях. Максимальные и минимальные значения вершин ромба при этом равны
(db)
b d
xд
+
+
=±
6
232
max ; max 6
a
yд=± . (4.91)
Размеры и форма ядра сечения для других конструктивных схем гусе-
ничных движителей приведены в работах [ ]. Следует заметить, что рас-
смотренные конструктивные и приведенные в [ ] схемы далеко не исчерпы-
вают все разновидности конструкций гусеничных движителей. Однако раз-
меры и форма ядра сечения их опорных площадей, как правило, превышает
таковые для других схем движителей.
Деформация несущих оснований под гусеничным движителем может
быть рассчитана по зависимостям проф. Ф.А. Опейко, которые получены на
основании формулы Герца. Для гусеничных машин эта зависимость имеет
вид
3ab2
E
p
h
г
г= ⋅ , (4.92)
где hг – средняя деформация несущего основания под гусеницей;
р – среднее давление по площади контакта.

Максимальная и минимальные деформации соответственно
max3 2
2maxE ab
p
h
г
= ⋅ ; h2minpEmin3ab2
г
= ⋅ , (4.93)
где pmax и pmin - максимальное и минимальное давления в пятне контакта.
4.4.5 Условия возможности прямолинейного движения
гусеничного движителя
Как и для горных машин на колесных движителях прямолинейное
движение машины на гусеничных движителях возможно при выполнении
двух основных условий:
- достаточности мощности;
- достаточности сцепления.
Первое из этих условий записывается точно так, как и для колесных
движителей
1000η
TT
д
Tv
N≥N= ⋅
, (4.94)
где Nд – мощность энергетических установок, передаваемая на гусеничный
движитель.
Для записи второго условия необходимо разделить силы сопротивле-
ния передвижению на внутренние и внешние, т.е. на силы сопротивления,
действующие внутри гусеничного движителя, и внешние силы сопротивле-
ния движению (рис.4.18).
Рисунок 4.18 – Схема сил, действующих на гусеничный движитель
при движении по прямой
При составлении этой схемы принято, что внешние силы сопротивле-
ния движению воспринимаются гусеницами поровну. Если теперь учесть ме-
сто приложения сил сопротивления движению, то условие достаточности
сцепления для гусеничного движителя можно записать в виде
fд″pab fкpab 2k′Tб
1
fд′pab 23
1
Р sinϕ
2
1
mg
dt
dv
c1m
2
1

fpab
dt
dv
2fд′⋅p⋅a⋅b+P3+m⋅g⋅sinϕ+C1⋅m2 ⋅ ⋅ ⋅, (4.95)
где f – коэффициент сцепления (трения) между гусеницами и опорным осно-
ванием.
Для обеспечения прямолинейного движения гусеничной машины необ-
ходимо обязательное выполнение этих условий, хотя в конкретных ситуаци-
ях может потребоваться и соблюдение некоторых других ограничений (пре-
одоление брода, габаритное ограничение и т.д.).
4.4.6 Поворот гусеничной машины
Горные машины, особенно для подземных разработок, работают в
стесненных по габаритам условиях, что требует хороших маневренных ка-
честв. Гусеничные движители, как уже отмечалось, удовлетворяют этим тре-
бованиям во многих случаях.
Рассматривая и устанавливая закономерности поворота, воспользуемся
теорией, разработанной проф. Ф.А. Опейко и его учениками [ , , ]. Со-
гласно этой теории гусеничная машина рассматривается как механическая
система, состоящая из трех тел: корпус и две гусеницы. Поворот осуществля-
ется за счет разных по величине скоростей перематывания гусениц и сопро-
вождается их скольжением по опорной поверхности. При этом движение гу-
сениц относительно корпуса и друг друга – прямолинейно поступательное.
Если рассматривать поворот гусеничной машины на достаточно жестком
опорном основании, т.е. считать движение опорных ветвей гусениц плоско-
параллельным, то план скоростей при повороте гусеничной машины можно
представить следующей схемой (Рис.4.19).
Рисунок 4.19 – Положение центров вращения опорных ветвей гусениц
и кинематика поворота
d
y
x
u2
C
u1
C1 C2 еу
e1 e2
R

Для определения радиуса и угловой скорости поворота машины рас-
смотрим её движение как сложное, состоящее из переносного и относитель-
ного. За переносное движение примем движение опорных ветвей относи-
тельно поверхности грунта, а за относительное - движение корпуса относи-
тельно опорных ветвей. На основании теоремы о сложении скоростей в
сложном движении запишем
ϑ=ϑe+ϑr, (4.96)
где v – абсолютная скорость точек корпуса;
ϑе - переносная (скорость скольжения цепей по залежи);
ϑr - скорость корпуса относительно опорных ветвей гусеничных лент.
В точках С1 и С2 – центры вращения опорных ветвей гусеничных лент –
переносная скорость равна нулю. Поэтому для точек корпуса машины, сов-
падающих с точками С1 и С2, выражение (4.96) примет вид
ϑ1=ϑr1, ϑ2=ϑr2 . (4.96)
Относительные скорости ϑr1 и ϑr2 корпуса равны скоростям перема-
тывания гусеничных лент u1 и u2, а их направление совпадает с осью Оу.
Таким образом, зная скорости лент u1 и u2 перематывания гусеничных це-
пей и смещения е1х , е1х , еу центров вращения их опорных ветвей, мы знаем
скорости двух точек корпуса машины. Так как движение корпуса по условию
считать плоскопараллельным, то это позволяет определить радиус и угловую
скорость поворота:
( )
( ) 2 1
21 12
2 1
2 1
2 uu
ue ue
uu
duu
R x x
−
⋅+ ⋅
+
−
+
= ;
(4.97)
e e d
uu
x+x+
−
=
1 2
ω 2 1 ,
где R – радиус поворота, за который принимается расстояние от центра С
вращения корпуса до его продольной оси;
ω – угловая скорость поворота;
е1 и е2 - боковые смещения мгновенных центров вращения (мгновенных
центров скоростей) опорных ветвей гусеничных лент относительно их про-
дольных осей;
u1 , u2 - скорости перематывания гусениц относительно корпуса;
d - поперечная база движителя.
Линия, на которой расположены центры вращения опорных ветвей гу-
сениц, остается перпендикулярной продольной оси машины и смещается от-
носительно центра симметрии на некоторое расстояние еу. Это положение

проф.Ф.А. Опейко доказал в математической теории трения [ ]. Действи-
тельно, выражая проекцию скорости какой-либо точки корпуса на ось Ох ис-
пользуя (4. ) и взяв за переносные скорости скорости центров вращения
опорных ветвей гусениц запишем
ϑx=ϑex+ϑrx=0+ω(y−yC), (4.96)
где у - координата рассматриваемой точки;
yC - продольная координата центра вращения.
Так как записанное соотношение справедливо для уС1 и уС2 ,
то уС1 = уС2 = еу, что и требовалось доказать.
Координаты центров вращения или их смещения е1, е2, еу могут быть
найдены из уравнений равновесия гусеничной машины при совершении по-
ворота. Рассматривая статический поворот, т.е. равномерный поворот гусе-
ничной машины без учёта сил инерции, эти уравнения (Рис.4. ) можно пред-
ставить в виде
Рисунок 4.20 – К составлению уравнений равновесия
гусеничного движителя при совершении поворота
0,
0,
0,
1 2
1 2
1 2
++=
++ =
++ =
MLL
PTT
PTT
y y y
x x x
(4.97)
где Рх – проекция равнодействующей внешних сил на ось Ох;
Ру – то же самое на ось Оу;
М – главный момент внешних сил относительно начала координат;
Т1х , Т2х , Т1у , Т2у - проекции равнодействующей сил трения между гусе-
ницами и грунтом на соответствующие оси;
L1 , L1 – моменты этих сил относительно геометрических центров гусе-
ниц.
Как проекции Т1х , Т2х , Т1у , Т2у , так и моменты L1 и L1 выражаются
интегралами
y
x
Т1х Т2х
Т1у Т2у
Рх
Ру
L1 М L2

=∫∫
1
1 1
S
Tx dTx; =∫∫
2
2 2
S
Tx dTx; =∫∫
1
1 1
S
Ty dTy; =∫∫
2
2 2
S
Ty dTy
=∫∫
1
1 1
S
L dL; =∫∫
2
2 2
S
L dL, (4.98)
где dT1=f⋅p1⋅dS1; dT2=f⋅p2⋅dS2;
dL1=f⋅p1⋅dS1⋅x12+y12; dL2=f⋅p2⋅dS2⋅x22+y22,
а интегрирование ведется по площадям S1 и S2 опорных площадок гусениц.
Вычисление этих интегралов приводит к очень громоздким выражени-
ям. Их качественное поведение изучено в работах [ , , ].
В связи с этим, в свое время были предложены упрощенные схемы гу-
сеничной машины в состоянии поворота, а также приближённые методы ре-
шения системы уравнений равновесия. Упрощения заключаются в замене
распределенных по опорным площадкам элементарных сил трения сосредо-
точенными силами, приложенными в некоторых характерных точках опор-
ных площадок гусениц. Автор наиболее распространенной теории поворота
гусеничных машин Ф.А. Опейко предложил приложить сосредоточенные си-
лы трения в геометрических центрах половин опорных площадок гусениц,
что позволило найти решение уравнений равновесия относительно смещений
центров вращения в некоторых частных случаях и на их основе построить
численные способы решения [ ]. Точные решения упрощённых уравнений
равновесия можно найти также при разбиении опорных площадей гусениц на
три части и приложении сосредоточенных сил трения в геометрических цен-
трах (Рис.4. ) получаемых при таком разбиении площадок [ ].
Рисунок 4.21 – К составлению уравнений равновесия
при разбиении опорных площадей гусениц на три равнее части
y
x
f1p1ab
3
1
Рх
Ру
М
О
С1 С2
d е2
а/3
ω
f2p2ab
3
1
е1
еу а

Тогда уравнения равновесия имеют вид
( ) ( )
( ) (3 ) 0
3
3
3
3
3
3
3
3
3
2
2
2 2
22 2 2
2
2
2
1
2 2
12 2 1
2
1
=
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
−
+
+
+ +
+
+
+
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
−
+
+
+ +
+
+
a e e
a e
e e
e
a e e
fpab a e
a e e
a e
e e
e
a e e
fpab a e
P
y
y
y
y
y
y
y
y
y
y
y
y
x
;
( ) ( )
3 (3 ) (3 ) 0
3 3
3
2
2
2
2
2
2
2
2
2
2
2
2 2
2
1
2
1
2
1
2
1
2
1
2
1 1
=
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
+
+
+ +
+
+
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
+
+
+ +
−
a e e
e
e e
e
a e e
fpab e
a e e
e
e e
e
a e e
fpab e
P
y y y
y y y
y
;
(4.99)
( ) ( )
( ) ( ) ⎟⎟−
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
+
+
+
+ +
+
+
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
+
+
+
+ +
+
2
1
2
1
2
1
2
1
2
1
2
1 1
2
2
2
2
2
2
2
2
2
2
2
2 2
3 3
23
3 3
23
a e e
e
e e
e
a e e
ddfpab e
a e e
e
e e
e
a e e
dfpab e
M
y y y
y y y
( ) ( )
( ) (3 ) 0
3
3
3
33
3
3
3
3
33
2
2
2 2
2
2
2
2
1
2 2
1
2
1
=
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
+
+ +
+
−
−
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
− +
−
+
+ +
+
−
a e e
a e
a e e
afpab a e
a e e
a e
a e e
afpab a e
y
y
y
y
y
y
y
y
В общем случае эта система уравнений (4.99) может быть решена отно-
сительно трех неизвестных е1, е2, еу только численными способами. Вместе
с тем точное решение может быть найдено для простейшего случая статиче-
ского поворота, под которым понимается поворот при отсутствии внешних
сдвигающих сил и равномерном распределении давления под гусеницами,
т.е. при Рх = Ру = 0, М = 0, Р1 = Р2 = 0. При таких условиях из первых двух
уравнений системы (4. ) следует, что е1 = е2, еу = 0. Обозначив, в этом слу-
чае. Равные боковые смещения центров вращения опорных ветвей гусениц
через е0 получим третье уравнение в виде

0
9
23
13
9
2
2
2
0
2
0
2
0 =
+
−
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+ ea
a
a
a e
e
d . (4.100)
Это уравнение преобразуется к квадратному относительно е0
0
81
16 9
9
16
3
2
4 2 2
0
2
2
0 =
− ⋅
− +
d
a ad
e
d
a
е , (4.101)
а его решение
d
aaa d
e
27
0=82−162+272. (4.102)
Это решение дает значения несколько меньше, чем по формуле (4.99)
d
a
e
8
2
0= . (4.103)
Но, самое главное отличие решения (4.102) от решения Ф.А. Опейко
состоит в том, что оно определяет основные параметры гусеничной машины,
при которых е0 =0, т. е. центры вращения находятся на продольных осях гу-
сеницы., а поворот машины происходит вокруг центра остановленной гусе-
ницы. Это достигается при
3
=4
a
d (4.104)
в условиях простейшего случая поворота.
Формула (4.103) находится решением уравнения
8a2−a16a2+27d2=0. (4.105)
При сравнительно небольших значениях Рх, Ру, М решение системы
(4.99) можно найти по формулам
e1=e0+Δe1; e2=e0+Δe2;
pbd
P da
ey x
⋅⋅
+
=
16
162 2, (4.106)
где е1, е2 - поправки решения, которые предложил проф. Ф.А. Опейко ис-
пользуя приближённое решение по методу Ньютона. Поправки Δе1 и Δе2
находятся по формулам

( ) ( )
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⋅
−
+
− ⋅ ⋅
−
⋅ ⋅ ⋅
+
Δ=
2 2 2 2
2
1 2
3
2 23
1
4
4
32 2 24
4
da
Md
da
P pp fab
fpdb
da
e y ;
(4.107)
( ) ( )
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⋅
−
+
− ⋅ ⋅
−+
⋅ ⋅ ⋅
+
Δ=
2 2 2 2
2
1 2
3
2 23
2
4
4
32 2 24
4
da
Md
da
P pp fab
fpdb
da
e y .
При больших значениях сдвигающих сил для достижения решения
уравнений равновесия гусеничной машины при повороте следует применить
ПЭВМ с программным обеспечением для решения систем нелинейных урав-
нений.
4.4.7 Мощность для выполнения поворота гусеничной машины
и условия возможности его выполнения
Двухгусеничная машина может выполнять повороты в нескольких ре-
жимах: с заданным и скоростями забегающей игусеницы от привода; при за-
торможенной отстающей гусенице; в условиях изменения скоростей отста-
ющей и забегающей гусениц. В том случае, когда обе гусеницы работают в
тяговом режиме мощность для поворота рассчитывается по формуле
1000η
T1u1T2u2
N=T⋅+T⋅ , (4.108)
где Т1Т, Т1Т – тяговые усилия забегающей и отстающей гусениц, соответ-
ственно.
Если отстающая гусеница заторможена или отключена от двигателя, то
мощность определяется выражением
1000η
T2u2
N=T⋅ . (4.108)
Для определения тяговых усилий гусеничных лент при повороте обра-
тимся к рисунку 4.21 и составим схему, подобную рис.4.18.
Тяговые усилия гусеничных лент при повороте, согласно этих рисун-
ков,
T1T=T1y+fд″⋅p1⋅a⋅b+k⋅p1⋅a⋅b+k′⋅T1б,
(4.106)
T2T=T2y+fд″⋅p2⋅a⋅b+k⋅p2⋅a⋅b+k′⋅T2б,
где Т1у, Т2у – продольные составляющие сил трения между гусеницами и
грунтом;

Т1б, Т2б – арифметические суммы боковых сил, действующих на гусенич-
ные цепи;
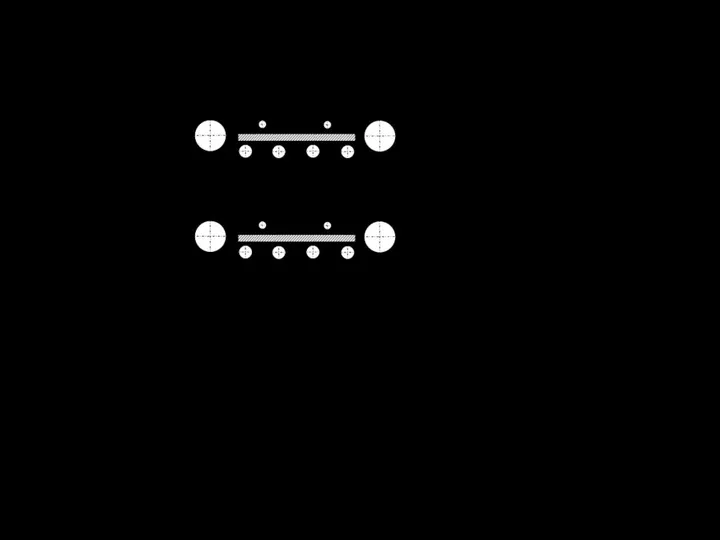
k′ - коэффициент сопротивления движению опорных катков по гусенич-
ным цепям за счет действия боковых сил (учитывает потери на трение между
боковыми поверхностями катков и направляющими гусеничных цепей).
Рисунок 4.20 – К определению тяговых усилий
гусеничных цепей при повороте:
а) – забегающая гусеница; б) – отстающая гусеница
Продольные составляющие сил трения между гусеничными лентами и
опорным основанием, а также арифметические суммы боковых сил (сохраня-
ем название, данное проф. Ф.А. Опейко), действующих между гусеничными
цепями и опорными катками согласно рис.4.21, определяются приближен-
ными формулами
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⋅ ⋅ ⋅
=− 1
9
2
3
2
1
2
1 1
1
a e
fpab e
Ty ;
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⋅ ⋅ ⋅
= 1
9
2
3
2
2
2
2 2
2
a e
fpab e
Ty ; (4.107)
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⋅ ⋅ ⋅
≅
2 1
1
2
1
1
39
2
3 e
e
a e
fpab a
Tб y;
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⋅ ⋅ ⋅
≅
2 2
2
2
2
2
39
2
3 e
e
a e
fpab a
Tб y. (4.108)
б) fд″p1ab fкp1ab k′Tб
Т1у
а) fд″p2ab fкp2ab k′Tб
Т2у

Последние формулы следуют из уравнений равновесия (4.99) двухгу-
сеничной машины при повороте и упрощены путем пренебрежения некото-
рыми малыми величинами. При их использовании необходимо учитывать,
что смещение может быть положительным (в сторону поворота), отрица-
тельным и при определённом сочетании внешних нагрузок и размеров гусе-
ничного хода - нулевым. При положительных смещениях центра вращения
отстающей гусеницы Т1у имеет отрицательное направление, т. е. эта сила пе-
редвигает гусеничную цепь, поэтому её необходимо притормаживать. Тор-
мозное усилие для остановки отстающей гусеницы, как следует из (4.107)
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
+
+
′⋅ ⋅ ⋅ ⋅
−″⋅ ⋅ ⋅− ⋅ ⋅ ⋅−
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⋅ ⋅ ⋅
=
2 1
1
2
1
1 1
2
1
2
1 1
1
2
2
1 3
9
2
3 e
e
a e
k fpab a
f pabkpab
a e
fpab e
Tтр д y
(4.109)
Это усилие реализуется обычно в приводе ведущих звёздочек гусениц,
тормозной момент на которых
MTтр=T1p⋅r, (4.110)
Войти в состояние поворота гусеничная машина может только при со-
блюдении некоторых условий, а именно, при достаточности мощности от
энергетических установок, передаваемой на гусеничный ход, а также при от-
сутствии полного буксования забегающей гусеницы. Эти условия обычно за-
писываются в виде
1000η
T1u1T2u2
N≥T⋅+T⋅ , (4.111)
или
1000η
T2u2
N=T⋅ при Т1у < 0.
Эти формулы выражают условие достаточности мощности.
Второе условие выражается соотношением
T2yf⋅p2⋅a⋅b, (4.112)
или используя приближённую формулу для вычисления Т2у
1
3
1
9
3
2
2
2
2
2 +
a+e
e . (4.113)

Отношение
2
2
2
2
2
2
2
2
2 9
39 =ρ
+ +
+
e a e
a e
(4.114)
называют коэффициентом запаса сцепления при повороте и условие доста-
точности сцепления записывают в виде
ρ21. (4.115)

4.5 Шагающие механизмы перемещения
Появление таких необычных и экзотических механизмов передвижения
горных машин обусловлено, прежде всего, необходимостью повышения их
производительности. Это, в свою очередь, потребовало увеличения энерго-
вооруженности и массы машин. Традиционные колесные и гусеничные
опорно-ходовые устройства позволяли обеспечить допустимые , особенно на
слабых несущих основаниях, давления на последние. Шагающие механизмы
перемещения, позволившие благодаря использованию большой по размерам
опорной базы, обеспечить сравнительно небольшие, порядка 250-1000 кПа,
давления на опорные поверхности, появились именно в горных машинах. В
последнее время шагающие механизмы перемещения получают применение
и в других областях производства (робототехнические системы).
Вместе с тем, следует отметить, что появление таких механизмов пере-
мещения в первую очередь связано с производством открытых горных работ
в больших объёмах. Такие механизмы перемещения применяются в драглай-
нах массой более 10 000 тонн и объёмом ковша более 150 м3. Существуют
различные системы обеспечения шагающего перемещения подобных машин
– чисто механические, электромеханические, гидромеханические и т. п.
Шагающие механизмы подобного типа (кривошипно-рычажные, экс-
центриковые) появились тогда, когда начали создавать экскаваторы высокой
производительности с большим объёмом ковша, а общая масса таких машин
приближалась к 1000 тонн. Самый мощный шагающий экскаватор-драглайн
«Биг Маски» 4250W был создан во второй половине 20-го века в США. Этот
гигант весил 13 500 тонн, имел ковш емкостью 168 м3, который подвешен на
стреле длиной 95 м. История создания экскаваторов-драглайнов восходит к
Леонардо да Винчи, а первый образец был изготовлен в США во второй по-
ловине 19-го века.
Рассмотрим шагающий механизм перемещения с частичным подъёмом
верхнего поворотного строения экскаватора (Рис. 4.23)
Такие механизмы в процессе шагания опираются на три площадки –
две лыжи и заднюю по ходу перемещения часть опорной базы. Процесс ша-
гания можно условно разделить на следующие фазы: опускание лыж, подъём
экскаватора, перемещение экскаватора относительно неподвижных лыж и его
опускание на опорную базу, подъём лыж. После этого цикл повторяется и
экскаватор перемещается на один шаг, длина которого составляет несколько
метров, чаще всего 2-3 метра.
Основная величина, благодаря которой появились экскаваторы на ша-
гающих движителях, среднее давление на грунт обычно вычисляется для
двух положений: при опоре на одну базу (Рис.4.23)
R2
mg
pб
⋅
⋅
=
π
, (4.116)
и при опоре на лыжи и частично на базу (Рис.4.24)

л
б
лF
R
p
=2
, (4.117)
где R – радиус опорной базы;
Rл – сила давления на лыжи.
Рисунок 4.23 – Принципиальная схема экскаватора
с шагающим механизмом перемещения:
1 – опорная база; 2 – механизм шагания;
3 – верхнее поворотное строение
z
O1
O2
B
A
l0 l3
l2
l1
h
l4
αl0 αА
αB
αl3
αl1 zB
zА
хВ
αl2
αl0
αВАх
φА
zС
xA
αl3z
zМ
xM
М
xC C
x
Х
Z
К ХМС O
ХКС
ZМС
βi
Dоб
vм

Для шагающих экскаваторов-драглайнов вопросы устойчивости имеют
особо важное значение, так как эти машины часто работают на техногенных
опорных основаниях, которые деформируются при сравнительно небольших
нагрузках. Кроме того, необходимо учитывать, что нагрузки со стороны ра-
бочего оборудования носят периодический характер при работе экскаватора
на одном месте. Поэтому чрезвычайно важно, чтобы центр давления не вы-
ходил за пределы ядра сечения. Так как опорная площадь – круг, то радиус
ядра сечения rяR
4
=1 .
Рисунок 4.24 – Ядро сечения шагающего экскаватора
Нагрузки на привод и элементы механизма шагания являются перемен-
ными и за один цикл шагания меняются в значительных пределах. При по-
стоянной скорости вращения приводных двигателей мощность, необходимая
для работы шагающего механизма передвижения меняется в таких же преде-
лах.
Мощность. Затрачиваемая на работу механизма шагания можно разде-
лить на две главные составляющие – мощность на подъём экскаватора и
мощность на его перемещение. Мощность для подъёма экскаватора можно
оценить по формуле
1000η
4
1 tц
mgH
N= ⋅ ⋅ , (4.118)
где m – масса экскаватора без учёта лыж;
Н – высота подъёма центра масс экскаватора;
tц – время одного шагания.
Вторая составляющая мощности – это мощность для перемещения экскава-
тора, которая тратится на преодоление трения между базой и несущим осно-
ванием. Она может быть выражена по формуле (Рис. 4.23)
1000η
4
2 ц
A
t
R fl
N= ⋅ ⋅, (4.119)
R
rя

где
л
c
A l
mgl
R= ⋅ ⋅ - сила давления базы на несущее основание;
f – коэффициент трения между базой и несущим основанием;
l – перемещение экскаватора на один шаг;
( )
л
Б c
Б
l
mgl l
R= ⋅ ⋅− - сила давления лыж на опорное основание.
Рисунок 4.25 – Определение мощности на перемещение
Третья составляющая затрат мощности – это мощность на перемеще-
ние подвижных частей механизма шагания, которая несравнима по величине
с двумя основными составляющими. Так как мощности N1 и N2 реализуются
поочерёдно, то мощность привода механизма шагания выбирается по одной
из них. Для механизма шагания, как опорно-ходового устройства, также су-
ществуют условия, при не выполнении которых движение невозможно. Пер-
вое из этих условий – это, как и ранее, условие достаточности мощности
η
η
1000
4
1000
4
2
1
ц
л
ц
д
t
R fl
N
t
mgH
N
N ⋅ ⋅
=
⋅ ⋅
=
≥ . (4.120)
Второе условие – это условие достаточности сцепления. Для шагающе-
го механизма перемещения это условие имеет вид
fб⋅RБfл⋅Rл, (4.121)
где fб , fл – соответственно коэффициент трения между опорным основанием
базой и лыжами.
mg
lc
RA lл RБ

4.6 Автономные и специальные механизмы подачи
Как уже отмечалось, у многих горных машин механизмы подачи сов-
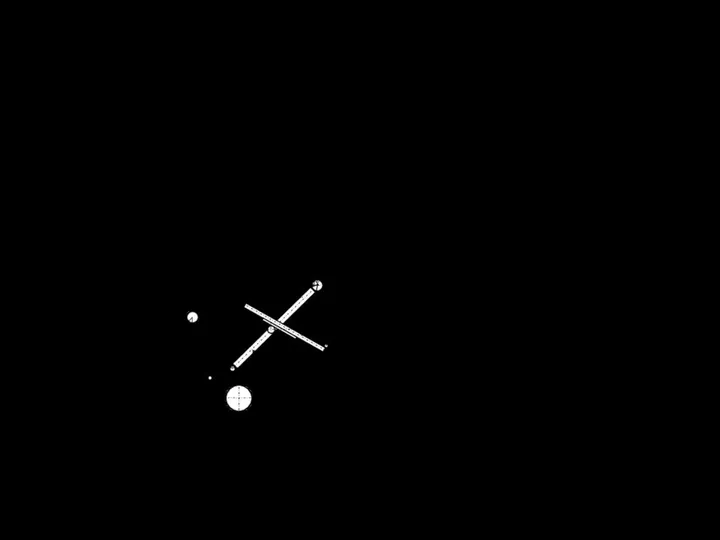
мещены с механизмом перемещения. Однако часть горных машин для выем-
ки полезного ископаемого имеют специальные механизмы подачи. К таким
машинам, прежде всего, относятся карьерные и вскрышные экскаваторы, ко-
торые выполняют работу не меняя положения своих опорно-поворотных
устройств в пространстве. Автономные механизмы подачи рабочего инстру-
мента на забой имеют проходческие комбайны избирательного действия,
проходческие щиты и ряд других машин. Некоторые машины имеют специ-
альные механизмы подачи рабочего инструмента на забой, например, буро-
вые машины, очистные комбайны и агрегаты. Чаще всего подобные меха-
низмы подачи основаны на использовании гидравлических, канатных, цеп-
ных, и зубчато-реечных (кремальерных) устройств. Примером автономного
механизма подачи является напорный механизм карьерных экскаваторов ти-
па прямая напорная лопата. Необходимость такого механизма диктуется ря-
дом причин, среди которых наибольшее значение имеет обеспечение без-
опасных значений угла откоса уступа. Наличием механизма напора один из
главных признаков отличия карьерных экскаваторов от строительных, мели-
оративных, дорожных экскаваторов с небольшим объёмом ковша. Как пра-
вило, такими механизмами напора карьерных экскаваторов бывают канатны-
ми, гидравлическими, зубчато-реечными.
Рисунок 4.26 – Механизм напора карьерных экскаваторов
типа прямая напорная лопата
Независимо от того, каким способом осуществляется подача ковша на
забой, соотношение скоростей подъёма ковша и напора должно быть таким,
чтобы обеспечивалось безопасное значение угла откоса уступа, т. е. скорости
тяги и напора должны обеспечивать выполнение условия
Тп
vт
vn
α
γ
β
Tт

cos 2 22
vт γ=vn+ωp⋅lp, (4.122)
где vт - скорость каната тяги;
β - угол между рукоятью и горизонталью;
α и γ - соответственно угол уступа и угол установки стрелы;
lp - длина рабочей части рукояти (расстояние между осью вращения ру-
кояти и соединением тягового каната с ковшом);
ωp - угловая скорость поворота рукояти.
Так как рабочая часть рукояти =∫ ⋅
t
lp vndt
0
, а при постоянной скорости
напора
lp=vn⋅t, (4.123)
где t - время работы механизма напора при выдвижении рукояти, то соотно-
шение (4.122) примет вид
vтcosγ=vn1+ω2p⋅t2. (4.124)
Это условие можно решить относительно скорости напора
1 22
cos
t
v
v
p
т
n
+ ⋅
=
ω
γ
. (4.125)
Таким образом, для сохранения постоянных значений толщин снимае-
мого ковшом слоя породы необходимо, чтобы скорость подачи рукояти из-
менялась по закону косинуса. Это легко реализовать при применении гид-
равлических механизмов напора.
Такие механизмы в настоящее время очень широко применяются, а об-
ласть их использования расширяется. Необходимое усилие подачи (напора)
чаще всего считается пропорциональным силе сопротивления резанию
Pn=Kn⋅Pp, (4.126)
где Kn - коэффициент пропорциональности.
Величина этого коэффициента меняется в значительных пределах и за-
висит как от свойств разрабатываемой породы, так и состояния резцов и ре-
жимов процесса резания. Величину силы резания можно вычислить по фор-
муле (4. )
Pp=ep⋅F, (4.127)

где ep - удельное сопротивление резанию (удельное сопротивление копа-
нию).
Примером организации подачи исполнительного органа являются про-
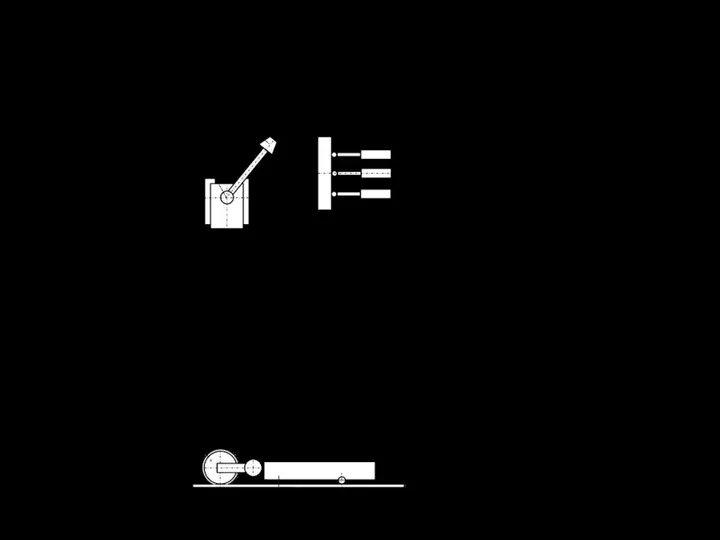
ходческие комбайны и комплексы с периодической подачей исполнительных
органов на забой (Рис. 4.27)
Рисунок 4.27 – Применение гидравлических механизмов подачи:
а) – комбайн избирательного действия;
б) – комбайн фронтального типа
В комбайнах избирательного действия, как правило, исполнительный
орган имеет три, а иногда и четыре, степени свободы, что позволяет при не-
подвижном комбайне отрабатывать всю поверхность забоя за счёт независи-
мых перемещений рукояти в вертикальной и горизонтальной плоскостях. Эти
перемещения могут реализовываться гидромашинами вращательного и по-
ступательного действия. В некоторых проходческих машинах, отрабатыва-
ющих одновременно всю поверхность забоя подача органа разрушения осу-
ществляется гидроцилиндрами, закреплёнными на неподвижном в этот пери-
од корпусе машины.
Канатные, цепные и зубчато-реечные механизмы подачи часто исполь-
зуются в тех случаях, когда непрерывное перемещение органа разрушения
является весьма значительным, например, при подземных разработках полез-
ных ископаемых длинными столбами с непрерывной подачей выемочных
машин на всю длину вынимаемого столба породы (Рис. 4.28).
R ωp
vn
vn
а) vn

б)
Рисунок 4.28 – Одношнековый очистной комбайн
Канатные и цепные системы подачи очистных машин являются выне-
сенными, так как тяговые механизмы таких систем находятся вне комбайнов.
В настоящее время большинство очистных комбайнов производится с так
называемыми бесцепными системами подачи. В таких системах необходимое
усилие подачи исполнительного органа на забой развивается за счёт упора
цевочного или зубчатого колеса, установленных на комбайне и приводимыхв
движение от источника энергии, также установленного на выемочной ма-
шине, на цевочную или зубчатую рейку, которые устанавливаются на ставе
забойного конвейера.
В некоторых выемочных машинах подача органов выемки породы мо-
жет осуществляться за счёт сил тяжести, например, ковш экскаватора-
драглайна. Это возможно при разработке сравнительно непрочных горных
пород, или при их предварительном разрыхлении.

5.1 Моделирование отвалообразователя
Для моделирования отвалообразователя принимаем следующие допу-
щения.
1. Отвалообразователь – динамическая система, состоящая из совокупно-
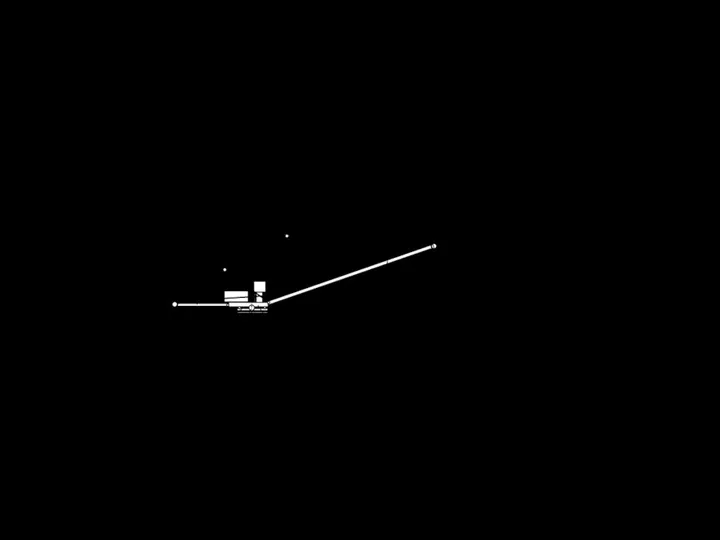
сти следующих элементов:
- база 1 (абсолютно жесткое тело);
- поворотная платформа 2 (абсолютно жесткое тело);
- отвальная консоль 3 (деформируемая сложная механическая система);
приемная консоль 4 (часть платформы);
- канаты, ванты 5 ,6 и 7 (элементы, связывающие между собой основ-
ные части);
- конвейер 8 (ленточный транспортер, установленный на приемной и
отвальной консолях, а также на поворотной платформе);
- механизм шагания 9.
2. деформации всех элементов, включая опорное основание, в пределах
закона Гука, т. е. пропорциональны напряжениям.
3. платформа относительно базы поворачивается вокруг оси цапфы.
Рисунок 5.1 – Схема отвалообразователя
Положение базы в пространстве определяем посредством углов Эйлера ψ,
ϕ, θ. В стационарном режиме считаем, что все углы малы, т. е. база совер-
шает малые колебания относительно положения равновесия под действием
случайных нагрузок, основная из которых – ветер. Тогда таблица направля-
ющих косинусов между главными осями инерции и осями неподвижной си-
стемы:
XYZ
А≈
1
1
1
θ ϕ
ψ ϕ
ψ θ
−
−
−
z
y
x
- таблица направляющих косинусов при малых от-
клонениях базы из натурального положения. Таблица – частный случай вра-
щения твердого тела при cosψ=cosϕ=cosθ=1, sinψ=ψ, sinϕ=ϕ, sinθ=θ.
4
5
3
1 2
6 7 8
9

Возьмем углы ψ, ϕ, θ за обобщенные координаты. Тогда ψ, ϕ, θ -
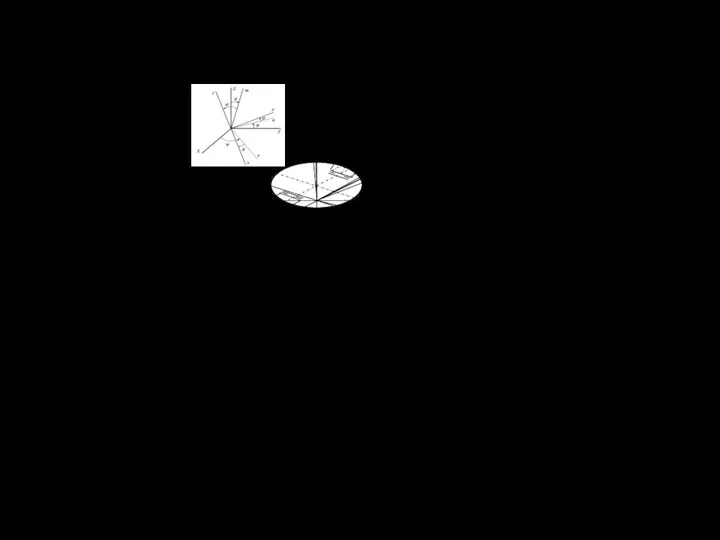
обобщенные координаты.
Квазискорости – проекции угловых скоростей на оси Ox, Oy, Oz.
Рисунок 5.1 – Пространственное положение опорной базы
Если вокруг оси Oz поворотов нет, то квазискорости определяются выраже-
ниями
5.2 Статический расчет наклона опорной базы
а) площадка, на которой стоит машина – горизонтальная
FR
Nr
F
N
p д
⋅
⋅
max=+4 ,
FR
Nr
F
N
p д
⋅
⋅
min=−4
если pmin=0, то rд=[rд]=rдmax=R4 - радиус ядра сечения базы.
rд=MyN, Му – момент внешних сил относительно оси Оу. Ось Ох совпада-
ет с линией наибольшего наклона.
h0 – средняя деформация.
R
N
h 2E
1 2
0
−ν
= или R
hp E ⋅
−
=+νπ
2
1 2
0 0 ;
P=Kh⋅h; Kh=π⋅R2(1E−ν2);
Z
Y
X
z
y
x
платформа
база
ϕ
θ
ϕ
ψ
θ

h=h0+r⋅cosα⋅tgθ, где θ – угол крена базы.
R
h h
tg
2
θ=max−min;
2
maxmin
0
h h
h= + ;
⎟
⎠
⎞
⎜
⎝
= ⎛+
⎟
⎠
⎞
⎜
⎝
= ⎛+
⎟
⎠
⎞
⎜
⎝
⎛+
= = ⋅ R
r
K
p
R
r
K
p
R
r
KF
N
K
p
h д
h
д
h
д
h h
4
max max 14 014 01 ;
⎟
⎠
⎞
⎜
⎝
= = ⎛−
R
r
K
p
K
p
h д
h h
4
min min 01 ;
h
д д
h
д д
h RK
pr
R
r
RK
p
R
r
R
r
RK
p
tg
⋅
⋅
=
⎦⎥= ⋅
⎤
⎣⎢
⎡+ −−
= ⋅ 2
0 08 40
2
4
14 1
θ2
;
Подставляем Kh и получаем
( ) ( ) ( )
3
2
0
2
2
20 1 2 21 21
R
Nr
R E
pr
RE E
pr R
tg д = − ⋅д=− ⋅д
⋅
⋅ ⋅−
θ= πν πν ν . (5.1)
Проверим этот результат, вычислив Му от давления
=∫∫ ⋅ ⋅
2π
00
R
My pdFrд, где rд – плечо относительно оси Оу.
rд=r⋅cosα.
Считая, как и ранее, что давление пропорционально деформациям
P=Kh⋅h, где h=h0+ry⋅tgθ,
имеем p=Kh(h0+r⋅cosα⋅tgθ)=p0+Kh⋅r⋅cosα⋅tgθ.
Тогда =∫∫(+ ⋅⋅α⋅θ)⋅α⋅ ⋅⋅α=
π
cos cos
2
00
M p0Kr tgrddrr
R
y h
=∫∫ ⋅ ⋅α⋅α⋅+∫∫ ⋅ ⋅α⋅θ⋅ ⋅α=
π π
pr ddr Kr tgdrd
R R
h
2 3 2
00
2
00
2
0 cos cos
= ⋅ ∫ + ⋅ ∫ ⋅=
π π
α θ αα
2
0
2 4 2
0
3
0 cos
4
1
sin
3
1
pR RtgKh d

π (ν)πθ (ν)θ
θ π tgRE tg
R
E
RtgKh R 3 2
2
4 4
1 21
2
4
1
4
1
−
⋅=
⋅−
= ⋅ ⋅= ; (5.2)
( ) ( )
3
2
3
2 1 22 1
ER
Nr
ER
M
tg y д
⋅
⋅−
=
⋅
−
θ= ν ν , см.стр.6, то же самое, Mдmax=N⋅rд.
Если считать угол θ малым и принять tgθ=θ, то записав My=C⋅θ можно
определить коэффициент угловой жесткости опорного основания под базой
( 2)
3
21−ν
Cд=E⋅R . (5.3)
5.3 Деформация опорного основания под опорной базой
1. Ядро сечения базы в форме кольца
Для нахождения радиуса ядра сечения, которое в силу симметрии имеет
форму круга, используем для нахождения напряжений в плоскости контакта
базы с опорным основанием формулы [1, 2], определяющие значения напря-
жений при сложном изгибе (внецентровом сжатии).
y
y
x
z x
W
M
W
M
F
P
p=± ± , (5.4)
где Рz - нормальная нагрузка на опорное основание;
Mx и My - моменты внешних нагрузок относительно соответствующих осей;
F - площадь опорной базы;
Wx и Wy - моменты сопротивления опорной площади относительно тех же
осей.
Список литературы:
1. Волков, Д.П., Черкасов В.А. Динамика и прочность многоковшовых экс-
каваторов и отвалообразователей. М.: Машиностроение. 1969. - 408 с.
2. Падерни, Р.Ю. Горные машины. М.: Недра. 1980. – 390 с.
3. Казаченко, Г.В. Определение пространственной ориентации горных ма-
шин // Горная механика. 2007. № 4. – С. 85-89.
4. Опейко, Ф.А. Торфяные машины // Ф.А. Опейко. – Минск: Выш. школа,
1968. -408 с.
5. Рудицын, М.Н. Справочное пособие по сопротивлению материалов / М.Н.
Рудицын, П.Я. Артемов, М.И. Любошиц. – Минск: Вышэйшая школа, 1970. -
638 с.

6. МАШИНЫ ДЛЯ ПОДГОТОВКИ ТОРФЯНЫХ МЕСТОРОЖДЕНИЙ
И РЕМОНТА ТЕХНОЛОГИЧЕСКИХ ПЛОЩАДЕЙ
№
п/п
Наименование
технологической операции
Марка ма-
шины
Рабочий орган Основные
парамет-
ры
1 Создание каналов осушительной
водоотводящей сети
ТЭ-3М
МТП-71
Драглайн или
Обратн.лопата
Lc=12,5м3
Vдр=0,5м3
2 Рытье канав регулирующей сети МТП-71
К-1Б
МТП-32
МТП-37
Профил.ковш
Мн.ковш.рама
Конусная фреза
Vпк=1м3
Vк1=45л
D=3,8 м
Кот=0,25
3 Сводка древесной растительности ЭТУ-0,7
МТП-13
МТП-43
Дисковая пила
на стреле
(Нпол=13м)
Dп=1,5 м
b=45 мм
vp=48 м/c
4 Разделка и погрузка деревьев РОП-3 Захват, прот.-
обрез.выд.устр
Dmaх=0,3м
5 Сплошная корчевка пней РКШ-1
КУП-4
МТП-26
МТП-81
Пас.роторы
Актив ротор
+сепаратор
+конвейер
N=5 шт
В=3,0 м
Н=0,4 м
6 Валкование пней и подкорчевка МП-3 КС Ротор с клыками В=2,4 м
α=54°
7 Погрузка пней в прицепы МТТ-12
МТП-29
Грейфер
Роторный
сепар.+конв.
mгр=1,3 т
В=3,0 м
Н=4,6 м
8 Вывозка деревьев и пней МТП-24 Прицеп-
самосвал
mгр=9 т
Vк+б.=20м3
9 Сбор мелкого пня СП-6,7
СПМ-1
Игл.барабан
Цепн.роторы
В=6,7 м
10 Фрезерование залежи с очесом и
древесными включениями
МТП-42 Фреза с чаш.
ножами
В=1,7 м
Н=0,4 м
11 Обогащение верхнего пласта залежи МЩФ-0 Вертикальная
винтов.фреза
Н=2,2 м
b=0,25 м
12 Укладка закрытого дренажа МЭД-1
МГД-6Н
Винт-фреза
Цепной бар
Мат.дрен.
Н=2,5м
13 Ремонт картовых канав РК-1 Конус.фреза 400м3/ч
14 Прочистка мостовых труб ПТМ-1 Вибр.головка НКФ-4
15 Профилирование и планировка по-
верхности карт
МТП-52
МТП-53
Фронтальная
шнек-фреза
В=5,7 м
α=(0-5)°

6.1 Одноковшовые экскаваторы
6.1.1 Экскаватор с механическим приводом
6 8 9
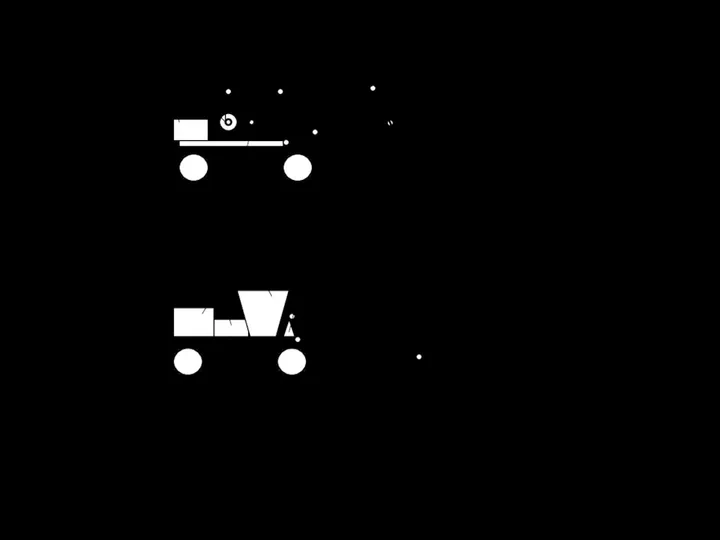
3 4 5
7 11 12 13
10
2 1 14
1 – гусеничный движитель;
2 – поворотная платформа;
3 – двигатель;
4 – двуногая стойка;
5, 6, 7 – лебедки поворота стойки и управления стрелой, тяговая лебедка;
8, 9, 10 – канаты подъемной лебедки, поворота стойки и тяговой лебедки;
11 – стойка; 12 – стрела; 13 – рукоять; 14 – ковш. Рис.6.1.1
6.1.2 Экскаватор с гидравлическим приводом
3 4 5 6 8 10
7
10
9
2 1 12
1 – гусеничный движитель;
2 – поворотная платформа;
3 – двигатель с насосной станцией;
4 – кабина с органами управления; 13
5 – стойка;
6, 7, 8 – стрела; 14
9 – рукоять;
10, 11, 12 – гидроцилиндры;
13 – подвижный четырехзвенник;
14 – ковш. Рис.6.1.2.

6.1.3 Мощность для привода тяговой лебедки экскаватора
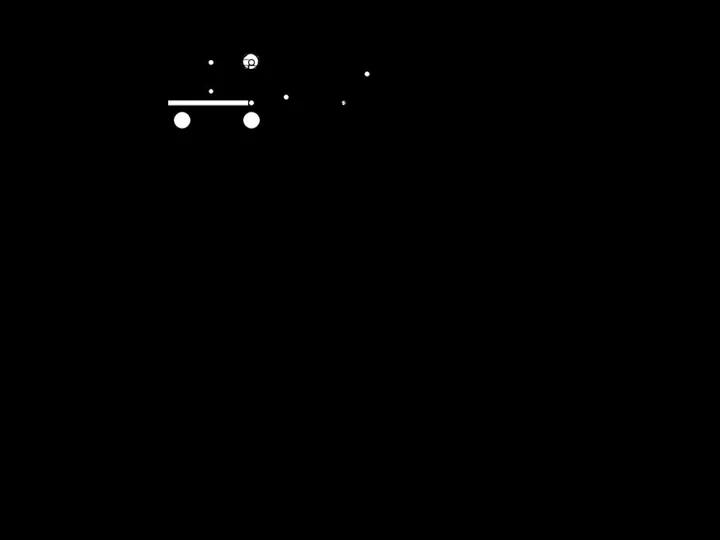
Рис. 6.1.3. Расчетная схема
к определению тягового усилия
Во время зачерпывания грунта канат тяговой лебедки имеет натяжение
S=S1+S2 , Н
где S1 - натяжение каната от действия силы сопротивления резанию грунта Р1;
S2 - натяжение каната от действия веса рукояти Gр, веса ковша с грунтом Gк+Gт.
Значения необходимых натяжений в тяговом канате определяются из урав-
нений равновесия моментов от действующих сил относительно точки А поворота
рукояти:
S1⋅H – P1⋅h1=0,
S2⋅H – (Gк+Gт)⋅h2 - Gр⋅h3=0.
Разрешив их относительно S1 и S2 получаем развернутое выражение
для определения суммарного натяжения в тяговом канате:
S=S1+S2=( P1⋅h1+(Gк+Gт)⋅h2+ Gр⋅h3)/H.
Усилие сопротивления резанию грунта Р1=рF,
где р – удельное сопротивление резанию грунта
( для торфяной залежи p=15000/δ, Н/м2);
F = δ⋅Bк – площадь поперечного сечения снимаемого слоя грунта, м2;
δ – толщина снимаемого слоя, м;
Bк – ширина ковша, м.
Мощность для привода тяговой лебедки
nл
T
T i
S
N
1000η.
ν
⋅ ⋅
⋅
= , кВт
где νТ – скорость наматывания каната на барабан лебедки, м/с;
i – кратность полиспаста;
ηп.л – КПД привода лебедки.
h3
h2
H
h1
S1+S2
P1
Gp
Gк+Gт
А
МТ.Л

6.2 МАШИНЫ ДЛЯ СВОДКИ ЛЕСА,
РАЗДЕЛКИ, ПОГРУЗКИ И ВЫВОЗКИ ДРЕВЕСИНЫ
6.2.1 Машины для сводки леса
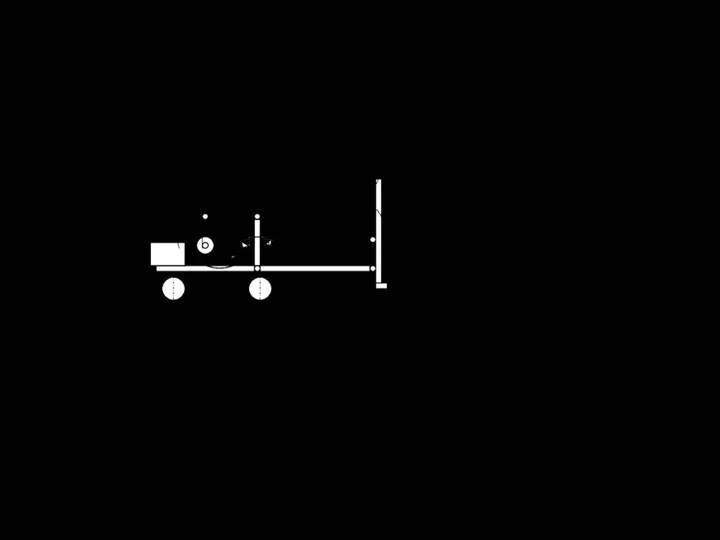
Наибольшее распространение в торфяной промышленности при подготовке
месторождений к эксплуатации, в частности, для сплошной сводки деревьев вместе
с кустарником получили машины ЭТУ-0,75 (ЭСЛ-4), МТП-13 и МТП-43.
С их помощью производится спиливание и укладка в валок деревьев с диаметром
у комля до 300 мм и высотой 16-18 м при ширине обрабатываемой полосы
за один проход 13-15 м. Машины выполнены на базе одноковшовых экскаваторов
ТЭ-2(3) , МТП-71 или погрузочного крана КПТ-1.
3 4 5 6 10
9
8
7
2 1
1 – движитель, 2 – поворотная платформа, 3 – двигатель, 4 – основная стойка с
приводными барабанами, 5 – стойка, 6 - стрела, 7 – дисковая пила с приводом,
8 – неподвижный диск, 9 – пакетирующее устройство, 10 - выталкиватель
Рис.6.2.1. Принципиальная схема
машины для сводки и пакетирования деревьев
Рабочее оборудование – дисковая пила с неподвижным диском над ней
и пакетирующее устройство вывешены на стреле, которая закреплена шарнирно
на поворотной платформе экскаватора и управляются тяговыми канатами или гид-
роцилиндрами. Привод пилы, в зависимости от базовой машины, механический че-
рез карданные телескопические валы и конический редуктор, гидро- или электро-
механический.

6.2.2 Валовая производительность машины для сводки леса
Валовая производительность машины для сводки леса:
Qc.л=(0,36⋅Вп⋅2πR(α/360)K1K2K3)/T, га/час
где Bn – ширина полосы захвата за один цикл, м;
R – радиус дуги, по которой проводится срез, м;
Т = t1 + t2 + t3 + t4 + t5 – продолжительность одного цикла, с;
К1 = 0,75 – коэффициент использования диаметра фрезы;
К2 = 0,9 – коэффициент использования ширины захвата;
К3 = 0,7 – КИРВ
Рис.6.2.2. Схема работы машины по сводке деревьев
Рабочий цикл состоит из следующих операций:
1. срезание древесной растительности на уровне кочек t1 = (9 11) c;
2. укладка срезанной древесины в навал, t2 = 5 с;
3. опускание дисковой пилы на уровень поверхности залежи, t3;
4. подрезка кочек и пней при обратном движении рабочего органа, t4;
5. передвижка машины вперед на длину L1 и установка оборудования вверх, t5.
R
α
L1
Вn
ωс

6.2.3 Энергия, необходимая для спиливания дерева
При спиливании дерева
источником энергии является двигатель,
а также накопленная кинетическая энер-
гия фрезы и вращающихся частей приво-
да. Она расходуется на резание и сообще-
ние кинетической энергии стружке.
Уравнение баланса мощности при спиливании дерева диаметром d
Адв + Афр = Ар + Ак.э ,
Адв – энергия двигателя, передаваемая к фрезе за время спиливания дерева;
Афр – энергия от вращающейся фрезы за счет уменьшения ее угловой скорости;
Ар – энергия, необходимая для резания одного дерева;
Ак.э – кинетическая энергия, сообщаемая древесной стружке.
Расчетами установлено, что энергиями Адв и Ак.э можно пренебречь,
т.к. они компенсируют друг друга, т.е. Адв ≅ Ак.э .
Энергия, передающаяся от вращающейся фрезы за счет уменьшения
её угловой скорости определим как разность кинетических энергий вращающегося дис-
ка, обладающего моментом инерции I, в начале и конце пиления одного дерева,
т.е. при угловых скоростях и
2
А=cI(ω02−ω12)
фр ,
где с = 1,1 – коэффициент, учитывающий моменты инерции вращающихся частей привода
фрезы;
ω0 – номинальная угловая скорость фрезы;
ω1 = 0,7ω0 – наименьшая допустимая угловая скорость фрезы.
Энергия, необходимая для резания одного дерева
Аррдрdb
4
⋅2
=π ,
где рдр= 1500000 ÷ 2000000 Н/м2 -удельное сопротивление резанию древесины;
d – диаметр спиливаемого дерева. м; b – ширина пропила, м.
Приравняв правые части уравнений по выражению энергий Афр и Ар и разрешив
относительно диаметра d получаем зависимость, по которой можно найти значение мак-
симального диаметра спиливаемого дерева при заданных параметрах фрезы и физико-
механических свойствах определенной древесины
p b
cI
d
др⋅ ⋅
⋅⋅ −
=
π
2 (ω02ω12)
max .
Например, для машины ЭТУ-0,75 максимально возможный диаметр спиливаемого
дерева равен 0,4 м.
ωi
ω
ω
d
D
ν
Рис. 6.2.3

6.3 Машины для глубокого фрезерования залежи с древесиной
Рабочим органом является горизонтальная фреза, на боковой поверхности которой
закреплены тарельчатые (чашечные) ножи. При поступательном движении агрегата
фронтальная фреза размельчает торфяную залежь вместе с очесом и древесными включе-
ниями и выбрасывает массу под задний прикатывающий каток.
Эффективная работа обеспечивается, когда зазор между кромкой отбойной плиты и
режущими кромками тарельчатых ножей равен (3-5) мм.
В конструкции фрезы применяются оригинальные опоры, позволяющие при
наружном диаметре по концам ножей 830 мм обеспечивать глубину фрезерования 400 мм.
Это достигается за счет встроенного цилиндрического редуктора с силовым корпусом.
Таблица 6.3.1 - Техническая характеристика машины МТП-42А
№ Наименование показателя
1
2
3
4
5
6
7
Тип
Ширина захвата, мм
Глубина фрезерования, мм
Фреза:
диаметр по концам ножей, мм
диаметр режущей кромки чашечных ножей, мм
общее число ножей, шт
частота вращения, об/мин
скорость резания, м/с
Рабочие скорости, м/ч
Движитель:
два передних опорных катка (диаметр/ширина), мм
задний прикатывающий каток
Эксплуатационная масса, кг
прицепная
1700
400
830
95
96
186/276
8/12
98-745
1000/700
1500/1700
5430

1 – передний отвал; 2 – ограждение; 3, 7. 15 – карданные валы; 4 – колесная тележка; 5 – цилиндрический редуктор; 6, 16 – ко-
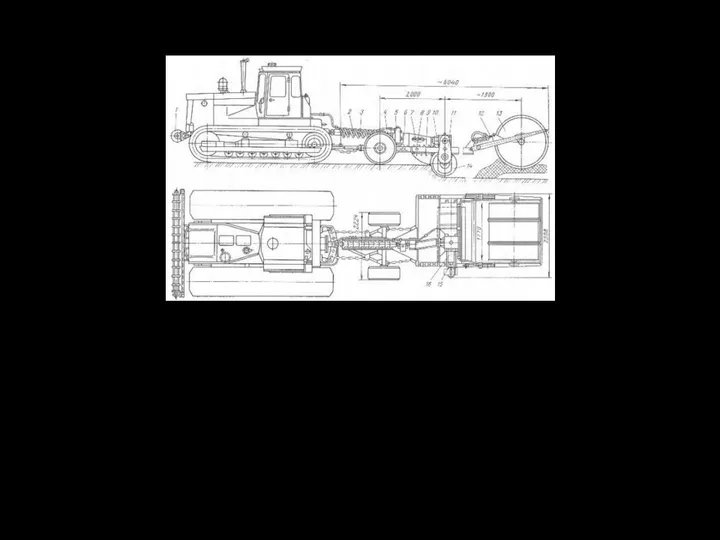
жухи; 8 – рама; 9 – отбойная плита; 10 – конический редуктор: 11 – редуктор: 12 – гидросистема; 13 – прикатывающий каток;
14 – фреза
Рис. 6.3.1 Схема машины МТП-42А

6.4. Канавные машины непрерывного действия
6.4.1.Определение рабочей скорости многоковшового экскаватора
для рытья картовых канав
Исходные данные:
1. Условия работы: залежь торфяная беспнистая;
2. Размеры канала, м: B = 1,26; ширина по дну b = 0.3; глубина Н = 2.0.
3. Конструктивные параметры многоковшовой рамы:
- расстояние между осями звездочек Lк= 5,4 м;
- ширина захвата b = 0,46 м;
- емкость ковша yк = 40 л;
- число ковшей z = 14 шт;
- шаг ковшей a = 0,88 м;
- угол наклона ковшовой рамы относительно горизонта α =500;
- скорость ковшовой цепи u=0,925 м/с.
4. Пластинчатый конвейер:
- рабочая длина L = 5,4 м;
- ширина ленты bк = 0,63 м;
- скорость vк = 1,3 м/с.
5. Четырехлопастной разбрасыватель:
- диаметр Dp = 0,5 м;
- ширина bp = 0,65 м;
- окружная скорость vp = 7,7 м/с.
6. Мощность двигателя машины: Nдв = 50 кВт.
7. Эксплуатационная масса многоковшового экскаватора m = 16700 кг.
Рис. 6.4.1 Расчетная схема
многоковшового экскаватора для рытья каналов
L
H
α
w
u
Pc
HB
Pк.р=Рп+Рр

Решение:
Уравнение баланса мощности при работе многоковшового экскаватора
во время рытья осушительного канала с одновременным транспортировани-
ем грунта в сторону и разбрасыванием его по поверхности месторождения
имеет вид:
∑
=
= =++++
n
i
NдвNiNNNNN
1
1 2 3 4 5, кВт.
1. Мощность на передвижение экскаватора
( )
1
0
1 1000η
μkmgw
N=+ , кВт
где (µ + k) = (0,08 + 0,05) –коэффициент сопротивления передвижению гу-
сеничного хода;
w0 – поступательная скорость экскаватора (кинематическая), м/с;
ŋ1= 0,7 – КПД трансмиссии машины.
2. Мощность на работу многоковшовой рамы включает две составля-
ющие:
2.1 Мощность на фрезерование торфяной залежи ковшами рабочего ор-
гана
2
?
21000η
pmQх
N= , кВт
где
δ
=15000
pm - удельные затраты энергии на резание торфяной залежи,
Н/м2;
δ 0(1ε)sinα
u
w
=a − - толщина стружки, снимаемой режущей кромкой
ковша, м;
έ = 0,05 – буксование движителя машины;
(1 )
2 0−ε
=+
QxBbHw - производительность по ходу, м3/с;
ŋ2 = 0,8 – КПД привода ковшовой рамы.
2.2 Мощность для подъема сфрезерованой массы на высоту разгрузки
из ковшей
2
?
21000η
gρQxHn
N= , кВт
где ρ = 980 – плотность сфрезерованной массы, кг/м3;
Нп= 0,5Н+НВ – высота подъема материала, м.

3. Мощность на работу горизонтального ленточного конвейера
3
31000η
fкqLvк
N= , кВт
где fк= (0,30…0,35) –коэффициент сопротивления перемещению материала
конвейером;
q = qn+ qт – погонная нагрузка от массы элементов конвейера и от
торфяной массы.
4. Мощность на сообщение ротором кинетической энергии сфрезеро-
ванной массе
4
2
421000η
ρ
= ⋅
Qc
N x , кВт
где с=2⋅vp - линейная скорость материала при сходе с лопаток ротора, м/с;
ŋ4 = 0,9 – КПД привода ротора.
5. Мощность на преодоление сопротивлений от скрепера и подачи
ковшовой рамы
1
0
5 1000
( )
η
PPw
N= c+n , кВт
где ⎟
⎠
⎞
⎜
⎝
= ⎛+−
c c bк
Bb
PpН
2
;
pc=0,5pm - удельные затраты энергии на резание залежи скрепером, Н/м2;
Рп=Рр(sinα+cosα) - сопротивление подачи ковшовой рамы, Н;
u
рQ
Рр=т x - сила резания торфяной залежи, Н.

6.4.2 Канавные машины с конусной фрезой
Для рытья и углубления картовых канав применяются машины непрерывного дей-
ствия серии МК с рабочим органом – конусная фреза. Оборудование МК-1,8 навешивает-
ся на экскаватор Т-3М, т.е. машина – МТП-32; или монтируется на одноосной колесной
тележке и работает в сцепке с гусеничным трактором Т-130Б, наименование – МТП-36
(МК-1.8П). Для предварительного осушения может устанавливаться фреза меньшего диа-
метра – МК-1.2
3 4 5 6 7 8 9
2 1 10
1 – движитель с нижней рамой, 2 – поворотная платформа, 3 – двигатель,
4 – основная стойка с приводным барабаном, 5 –поворотная стойка, 6 - стрела,
7 – привод, 8 –конусная фреза, 9 –направляющий кожух, 10 – опора
Рис.6.4.2. Канавная машина МТП-32 с конусной фрезой на базе экскаватора
Таблица 6.4.2 Технические данные канавных машин с конусной фрезой
№ Наименование показателя МТП-32 МТП-32П МК-1.2
1
2
3
4
5
6
7
Диаметр фрезы, м
Частота вращения, мин-1
Общее количество тарельчатых ножей
Наибольшая глубина канавы, м
Рабочие скорости передвижения, м/час
Производительность, м3/час
Эксплуатационная масса машины, кг
4.0
140
48
1.8
280-350
180-270
4.0 без экс.
4.0
140
48
1.8
150-350
180-270
6.9
2.8
218
36
1.2
150-350
100-120
6.5
Параметры картовой канавы в поперечном сечении характеризуются:
Н - глубина канавы, м
B = 0.3 м - ширина по дну;
Заложение откосов в торфяной залежи – α=0.25
для минеральных грунтов – (0.5, 0.75 или 1.0)
В = 2α·Н+b – ширина канавы на поверхности, м.
ω
В Н
b
Н
В
Рис.6.4.3.

а – вид сбоку; б – вид сзади;
1 – конусная фреза; 2 – опорная лыжа; 3 – сцепка;
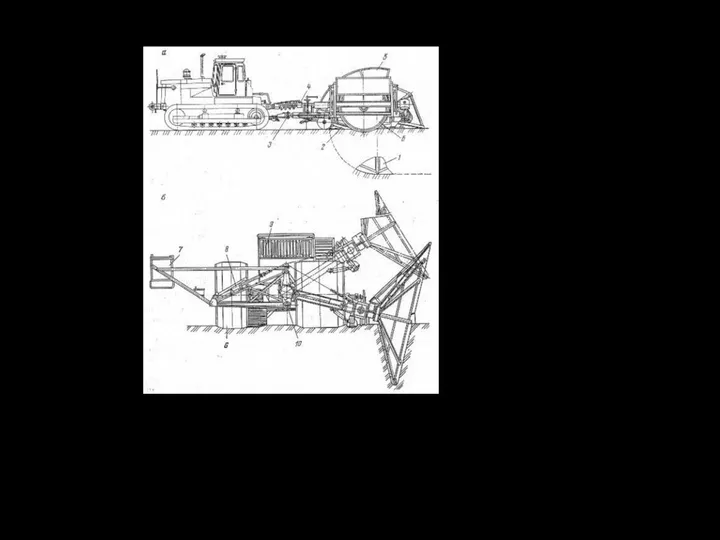
4 – трансмиссия; 5 – кожух; 6 – колесный движитель; 7 – контргруз;
8 – гидросистема; 9 - решетка; 10 - подвеска
Рис. 6.4.4 Схема канавной машины МТП-32А

Таблица 6.4.2 - Техническая характеристика канавных машин
№ Наименование показателя МТП-32А МТП-32Б
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Тип
Частота вращения фрезы, об/мин
Диаметр фрезы по концам ножей, мм
по большему основанию
по меньшему основанию
Диаметр чашечного ножа, мм
число ножей, шт
общее
в плоскости резания
Параметры отрываемой канавы:
глубина (максимальная), мм
ширина по дну, мм
заложение откосов
Транспортные скорости, км/ч
Производительность, м3/ч
Параметры движителя, мм:
диаметр катков
ширина (левый/правый)
гусеницы (ширина/опорная длина)
Габаритные размеры, мм
длина
ширина
высота в транспортном положении
Дорожный просвет, мм
Масса машины без контргруза, кг
Масса контргруза, кг
Давление на грунт, кПа
Прицепная,
колесная
151
3800
150
120
42
2
1800
200
0,25
2,3-5,4
140-240
1800
1216/2000
-
5475
8830
5400
525
8990
1050
24
Прицепная,
гусеничная
154
3800
150
120
42
2
1800
200
0,25
2,3-5,4
140-240
-
-
750/3720
6730
8900
4370
400
9155
2000
20

6.4.3 Условие достаточности производительности конусной фрезы
Производительность фрезы по ходу агрегата
определим как произведение площади поперечно-
го сечения канала (трапеция) на поступательную
скорость:
Qx=Fν=0.5(B+b)Hν, м3/с
Конструктивная производительность фрезы за
один оборот равна
t
V
Qфkp
1= ⋅1
ϕ
, м3/с
где ϕ = (0,8…0,9) – коэффициент заполнения про-
странства, ограниченного высотой тарельчатых
ножей,
kp= (1,2…1,5) - коэффициент разрыхления
массы в результате фрезерования;
t = 60/n – продолжительность одного обо-
рота, с/об.
Объем торфа, снимаемый фрезой за один оборот,
V1=lh⋅2πρ=lh⋅π(R+r),
где lh – площадь поперечного сечения снимаемого слоя;
ρ=(R+r)/2 - средняя длина окружности по боковой поверхности фрезы.
Тогда производительность фрезы в единицу времени
ϕ π ϕ ( )ω
( )602klhRr
n
lhRr
Qф=kp⋅ + = p + .
Условие достаточности производительности конусной фрезы: Qф≥Qx.
Выразим максимальную толщину снимаемого слоя или высоту рабочего простран-
ства фрезы, которые определяется ее геометрическими и кинематическими параметрами:
ω
ν
ϕ + ⋅ ⋅
+
≥ ⋅
l
H
Rr
kBh
h p .
Для того, чтобы весь торф, снятый тарельчатыми ножами, помещался в рабочем
пространстве фрезы, необходимо соблюдение еще одного условия – высота тарельчато-
го ножа должна быть больше максимальной толщины снимаемой стружки
h≥δmax,
т.к. в противном случае снятый слой будет упираться в боковую поверхность
конуса, что приведет к существенному увеличению энергии на фрезерование.
Выражение для определения максимальной толщины стружки, снимаемой ко-
нусной фрезой, имеет вид
D
H
D
H
=z⋅ ⋅2 ⋅1−
2
max ω
πν
δ ,
где z=(bн⋅i)/B≅5 - число ножей в плоскости резания.
H
B
d ω
l
D
b
h
Рис. 6.4.5

6.4.4 Мощность для работы канавной машины с конусной фрезой
Суммарная мощность, необходимая для работы машины с конусной фре-
зой, включает четыре составляющих:
N=N1+N2+N3+N4 , кВт.
Мощность на передвижение:
∙ для самоходной гусеничной машины с навесной конусной фрезой -
1
1 2 0
1 1000
( )
η
μμmgν
N=NГ=+ М ,
∙ прицепной машины в составе с гусеничным трактором –
1000
(1 )
1000
0
1
0
1
μ ν ε
η
μ ν+ −
N=NT+NM= гmTg кmПg ,
где mМ, mT и mП – эксплуатационные массы самоходной машины, трактора и при-
цепной колесной машины, соответственно, кг;
μг=(μ1+μ2) и μк – коэффициенты сопротивления передвижению машин с гу-
сеничным и колесным движителями;
ν0 – кинематическая скорость движения машины, м/с;
ε - буксование активного движителя самоходной машины или тягача.
Мощность на фрезерование торфа N3 и пня N4:
2 2
2 3 . . 1000 1000
(1 )
η
α
η
αтх пнx
фт фп
pQ pQ
N+N=N+N=− + ,
где pm=20000δ - удельные затраты энергии на фрезерование торфа, Н/м2;
δ=2πν/ω - толщина стружки, м;
α=α; α≅α0 – местная и средняя пнистость торфяной залежи;
рпн=(70…100)рт - удельные затраты энергии на фрезерование пня, Н/м2;
Qx=Fν=0,5(B+b)H⋅ν0(1−ε) - производительность по ходу, м3/с;
η1 и η2 – КПД трансмиссии движителя и привода шнек-фрезы.
Мощность на сообщение кинетической энергии сфрезерованной массе
2
2 2
4 . 2 2000η
ρQv
c
t
mv
N=Nкэ= = x ,
где с=1,2 – коэффициент, учитывающий повторное соударение ножей с фрезеруе-
мой массой;
ρ≅1000 кг/м3 – плотность сфрезерованной массы;
v=ωфRф=πDn/60 – окружная скорость фрезы по наружному диаметру, м/с.
Если в первое уравнение вместо суммарной мощности N подставить значе-
ние эксплуатационной мощности двигателя Nдв, обеспечивающего работу машины,
то получаем уравнение баланса мощностей
Nдв=N1+N2+N3+N4,,
решив которое относительно ν0 получим ту наибольшую теоретическую, поступа-
тельную скорость, при которой максимально реализуется мощность двигателя.

6.5 МАШИНЫ ДЛЯ РЕМОНТА ОСУШИТЕЛЬНОЙ СЕТИ
6.5.1 Шнеко-роторная машина для ремонта картовых канав
Содержание в рабочем состоянии открытой осушительной сети на разраба-
тываемых торфяных месторождениях сопряжено с выполнением большого объема
работ по их периодическому ремонту. Например, только на технологической пло-
щадке (500х1000)м общей площадью 50 га развернутая длина картовых канав, при
ширине карт 20, 30 или 40м, составляет 10-20км.
Для ремонта (очистка и углубление), картовых канав широко применяются
канавные машины РК-0 и РК-1. Рабочее оборудование – конусная шнек-фреза с ро-
тором-метателем и напорным щитом – смонтировано консольно на телескопиче-
ской рамке, которая закреплена шарнирно с правой стороны по ходу на одноосной
колесной тележке. Машина работает в агрегате с гусеничным трактором кл.тяги 3,
или с колесными - кл.тяги 1.4 и 2. Привод – механический от ВОМ через кардан-
ный телескопический вал, два конических редуктора и промежуточный вал с цеп-
ными муфтами. Перевод оборудования в рабочее или транспортное положения –
два силовых цилиндра, подключенные к отдельным секциям распределителя гид-
росистемы трактора.
Основные технические данные машины РК-0:
1. производительность машины по рабочему органу, м3/ч – 350
2. глубина очистки, м до 1.8
3. дальность отбрасывания гидромассы, м – до 14
4. рабочие скорости передвижения, км/ч 1,3-2,4
5. масса с контргрузом, кг 2450
6. параметры конусного шнека:
диаметры min/max, мм 200 / 400
шаг витков, мм переменный (150-300)
частота вращения, с-1 9,0
7. ротор-метатель:
диаметр/ширина, мм 600/200
окружная скорость по концам лопаток, м/с 16,7
8. катки движителя: кол-во; (диаметр/ширина), мм 2х(600/1000)

6.5.2 Производительность ротора шнеко-роторной машины
Для нормальной работы каналоочисти-
тельной машины должны соблюдаться два
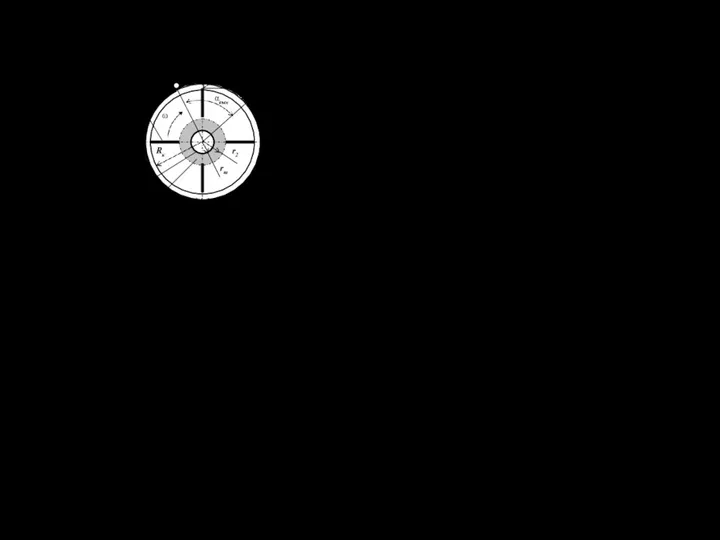
условия достаточности производительности
центробежного колеса :
- по выходному цилиндрическому сече-
нию кожуха (сектор с углом αвых);
- по входному, плоскому сечению Fв в
центробежное колесо.
Толщина стружки грунта, снимаемого
одной лопаткой колеса должна быть меньше
ширины лопатки.
Площадь выходного сечения кожуха 3:
π
α
π
2
Fвых= ⋅Rк⋅bк⋅вых,
где αвых – центральный угол, охватывающий
дугу выходного сечения кожуха, рад;
Dк=2Rк – наружный диаметр колеса,
примерно равен диаметру кожуха.
Производительность по выходному сечению кожуха
2
2
2
2
2 αν
ϕ ϕ
кквых
p
вых
p
Db
Q=kFu=k
,
где u2 ≅ v2 – принимается для разрыхленной торфяной массы с влагой более 85%;
ϕр=0,7 – коэффициент заполнения пространства ротора торфяной массой;
kp=1,5 – коэффициент разрыхления.
Производительность Q2 должна быть больше производительности шнека
Qш по ходу машины ш ос
p
ш
QшkπR rν
ϕ
= (2−02) ,
где ϕш=0,7 - коэффициент заполнения пространства между витками шнека;
νос=ϕврН/t – осевая скорость продвижения торфяной массы в шнеке, м/с;
ϕвр=0,1…0,3 – коэффициент вращения торфяной массы вместе со шнеком;
Н– средний шаг витков шнека, м;
t - время, за которое масса перемещается на один шаг, с; для однозаходного
шнека t=60/n=2π/ω.
Приравняв производительности Q2 и Qш и разрешив уравнение относительно
bк найдем достаточную ширину выходного сечения кожуха
Н
R
R r
b
к
ш
вых
вр
к 2
2
0
2
2 2
−
≥ ⋅
α
ϕ
,
С другой стороны bк>=vnt , где vn= vмcosβ – проекция скорости передвижения
машины в направлении оси вращения шнека, наклоненной к горизонту по углом β;
t=2π/(ωz) – время поворота многозаходного z шнека не один шаг витка, с.
Тогда последнее условие - β
ω
π
2vcos
bк≥z⋅ .
ω
r2
αвых
Fв
υ2
Rк
rт
2
3
1
u2 с
4
Рис. 6.5.1

6.5.3 Скорость частиц при сходе с лопаток. Дальность бросания
Для разжиженной торфяной массы силы трения этой массы о поверхность
лопаток малы, поэтому при инженерных расчетах ими можно пренебречь. Тогда
(см.рисунок 3.6.2) можно записать, что u2 ≅ v2 и α2 ≅ 45о.
Абсолютная скорость частиц при сходе с лопаток - с=2ν2.
Дальность бросания торфяной массы лопатками ротора а также наиболь-
шую высоту ее полета определим на классической модели, имитирующей движе-
ние материальной точки без учета сопротивления среды.
Уравнения движения частицы:
x=c2cosα2⋅t;
y=c2sinα2⋅t−gt2/2.
Из первого уравнения выразим t и подста-
вим его значение во второе. Тогда
2
2 2
2
2
α22ccosα
gx
y=x⋅tg− .
Продифференцируем функцию и приравняем ее к нулю, т.е. dy/dx=0.
Окончательно: высота полета
H g
2
2
max2
=1ν
; дальность бросания Lmax=2ν22/g.
6.5.4 Мощность для работы ротора-метателя канавной машины
Мощность для работы ротора канавной машины включает три слагаемых:
1. Мощность для съема грунта
ш
cxш
c
pQ
N
1000η
= . , кВт
где рс≅ 1000 Н/м2 – удельный расход энергии на съем торфяной массы с помощью
лопаток ротора;
Qх.ш – производительность шнека по ходу машины, м3/с;
ηш – КПД привода рабочего органа;
2. Мощность на волочение торфяной массы по неподвижному кожуху
ш
хш
np
ш
xш
в np
Q
fQ f
t
т
N
η
ρν
π
α
π
α
η
ν ρν
2 21000 2 4000
2
.2
2
.2
2
2 ⋅=
= = ⋅
, кВт
где fпр≅ 2…3 – приведенный коэффициент трения торфяной массы по внутренней
поверхности кожуха;
α= 2π - αвых – угол, соответствующий поверхности кожуха ротора, рад;
ρ = 1000 кг/м3 – плотность торфяной массы;
ν2 – окружная скорость по концам лопаток ротора, м/с;
3. Мощность на сообщение кинетической энергии разбрасываемой массе
ш
хш
ш
хш
кэ
Qс Q
N
η
ρν
η
ρ
21000 1000
2
.2
2
.
. =
= ⋅
, кВт
где c=2ν2 - абсолютная скорость частиц при сходе с лопаток ротора, м/с.
L
c2 Hmax
α2
y
х
Рис. 6.5.2

6.6 ДРЕНАЖНЫЕ МАШИНЫ
6.6.1 Машины для устройства закрытого дренажа
Технологические требования к машинам по устройству закрытого дренажа:
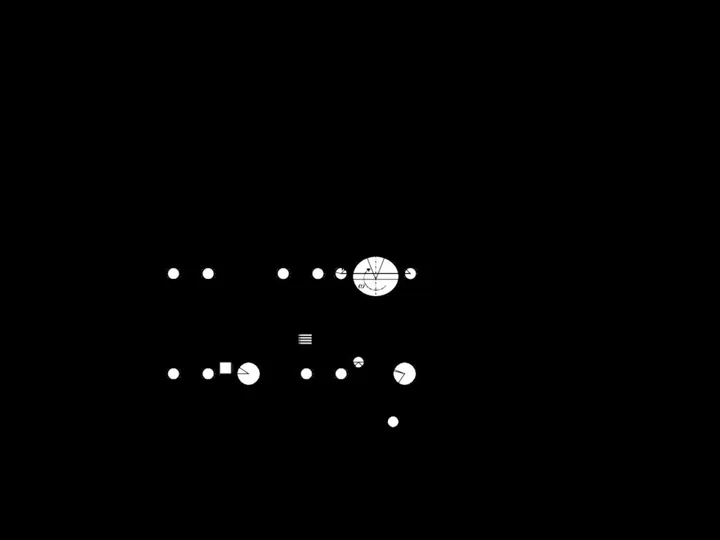
1. Обеспечивать устройство дренажа с заданным углом не зависимо от
рельефа поверхности;
2. Прокладывать дрены на заданную глубину (1,5-2,5) м;
3. Обеспечивать правильное сопряжение дрен с закрытыми и открытыми
каналами;
4. Комплексная механизация всех операций по устройству дренажа;
5. Допускать постоянный контроль качества дрен.
Дренажные машины классифицируются
по назначению и виду прокладываемого дренажа:
- машины для устройства материального дренажа из труб и пористых мате-
риалов (гончарные трубки, пластмассовые трубы в бухтах);
- машины для устройства кротового и щелевого дренажа;
по типу и устройству рабочего органа:
- цепной многоковшовый;
- скребковый (цепной бар);
- роторный многоковшовый;
- дисковая фреза;
- вертикальный нож;
- шнек-фреза.
Н=(0,7-1,5) м Н=(0,9-1,0) м
а) пассивный нож - машина ДДМ-5
«кротодренаж» на беспнистой залежи; б) дисковая качающаяся фреза;
Н=1,5 м Н=2,5 м
машина ДВМ-5 МТП-39
в) шнек-фреза г) цепной бар
(внизу - большего с устройством закладки
диаметра); дренажных труб из бухты;
В торфяной промышленности нашли применение машины с цепным баром
(навесные: МГД-3 на экскаваторе ТЭ-3 или МТП-39 на тракторе Т-130Б), а также
со шнек-фрезой (прицепные и навесные типа ДВМ и МЭД).
В мелиорации широкое применение получили экскаваторы-дреноукладчики
типа ЭТЦ и канавные машины К-1Б с рабочим органом – многоковшовая рама и
со специальным оборудованием для укладки гончарной трубки.
Н
Н Н
Н
w
w
Vр
ω
w
w
ω
ω
w
w
w
w
2ά

Рис. 6.2. Машина глубокого дренирования МТП-39 на тракторе С-100Б
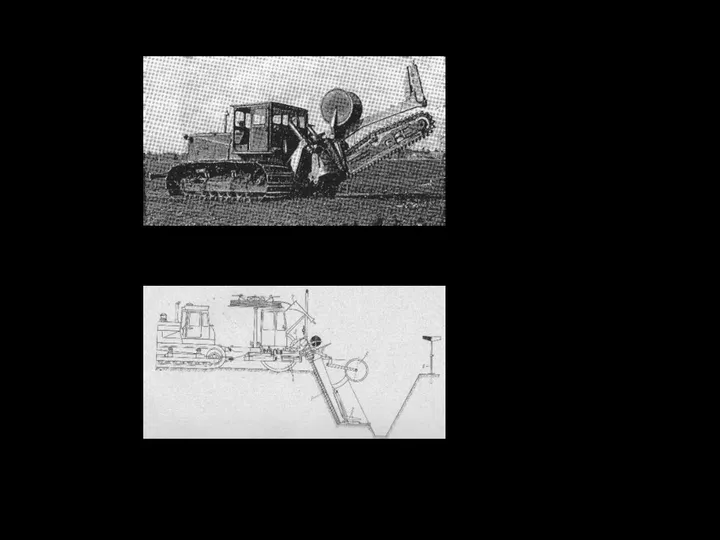
1–рабочий аппарат (винтовая фреза); 2 – трубоформователь; 3 – редуктор;
4 – колесный движитель; 5 – закрывающий аппарат;
6 – визирное приспособление; 7 – механизм подачи трубок
Рис. 6.6.1 Общий вид машины по закладке пластмассового дренажа

6.6.2 Мощность для работы цепного бара дренажной машины МТП-39
Суммарная мощность при работе цепного бара включает четыре составля-
ющих:
Nц.б=Nф.т+Nф.п+Nк.э+Nп.м , кВт.
Мощности на фрезерование торфа и древесных включений (пней) выра-
жаются через удельные сопротивления резанию указанных материалов, которые
зависят от толщины снимаемой стружки и их физико-механических характеристик,
и производительность по ходу, т.е. Nф=f(pт , pп , Qx):
2 2
. . 1000 1000
(1 )
η
α
η
αтх пx
фт фп
pQ pQ
N+N=− + ,
где pm=15000δ - удельные затраты энергии на фрезерование торфа, Н/м2;
δ=a(ν/u)sinα - толщина стружки, м;
a – шаг установки резцов на тяговой цепи бара, м;
u – скорость цепи с резцами, м/с;
α=α; α≅α0 – местная и средняя пнистость торфяной залежи;
рпн=(70…100)рт - удельные затраты энергии на фрезерование пня, Н/м2;
Qx=Fν=bH⋅ν0(1−ε) - производительность по ходу, м3/с;
b и Н – ширина и глубина прорезаемой щели прямоугольной формы, м;
η1 и η2 – КПД трансмиссии движителя и привода рабочего органа.
Мощность на сообщение кинетической энергии отбрасываемому материа-
лу
2
2 2
. 2 2000η
ν ρцνр
кэ
Q
t
m
N= = , кВт
где ρ - плотность сфрезерованной массы, кг/м3;
υр – скорость по концам резцов цепного бара, м/с.
Мощность на подъем материала на высоту Нп
2
. 1000η
ρ цn
пм n
gQH
N=mgH= , кВт
где
u
a
V
tk
V
Qkp p
ц з
ϕ ϕ
= ⋅= - производительность цепного бара, м3/с;
ϕз=0,9 – заполнение пространства между резцами;
kp=1,2 – коэффициент, учитывающий разрыхление материала;
V=bah – объем пространства между соседними резцами, м3;
b, a, h – ширина, шаг установки и высота резцов, м.
Для обеспечения устойчивой работы щеленарезной (дренажной) машины с
цепным баром должно соблюдаться следующее условие Qц≥Qx,
т. е. производительность по рабочему органу должна быть больше про-
изводительности по ходу машины.

6.6.3 Мощность для работы шнек-фрезы дренажной машины
Мощность для работы шнек-фрезы дренажной машины включает затраты на
фрезерование торфа и древесных включений, а также мощность для обеспечения
транспортирования витками шнека сфрезерованной массы,
Мощности на фрезерование торфа и древесных включений (пней)
2 2
. . 1000 1000
(1 )
η
α
η
αтх пx
фт фп
pQ pQ
N+N=− + , кВт.
Мощность для обеспечения транспортирования витками шнека сфрезе-
рованной массы
1000η2
τω
Nтр=ϕвр S
,
где ϕвр=(0,5…0,7) – коэффициент, учитывающий наличие вращения торфяной мас-
сы вместе с витками шнека;
τ =5000 Н/м2 – сопротивление сдвигу торфяной массы;
ω - угловая скорость шнек-фрезы, рад/с;
η2 - КПД привода рабочего органа.
S – статический момент поверхности соприкосновения транспортируемой
массы с окружающим пространством относительно оси вращения шне-
ка, Н⋅м:
S=2πR⋅lR=2πR2l.
закрывающий
аппарат
Рис.6.6.2
Учитывая, что рабочий орган дре-
нажной машины состоит из двух шнек-
фрез с основным диаметром по концам
режущих кромок D1 на длине l1 и ниж-
ним хвостовиком длиной l2 несколько
большего диаметра D2 , то статический
момент следует определять по следую-
щей формуле
S=2π(R12l1+R22l2), Н⋅м.
Мощность на подъем массы на
поверхность дрены
2
.1000η
ρgQH
Nпм= x .
Последнюю составляющую, вви-
ду сравнительно небольших значений,
при общих расчетах не учитывают.
Сопротивление закрывающего
аппарата, как пассивного движителя,
выполняющего и технологическую
функцию, учитывается через затраты
мощности на передвижение машины.
l2
l1
b1=D1
b2=D2

6.7 МАШИНЫ ДЛЯ КОРЧЕВКИ, ОЧИСТКИ И ПОГРУЗКИ ПНЕЙ
6.7.1 Машины для сплошной корчевки, сепарации, валкования и по-
грузки пней и древесных включений
Для подготовки торфяных месторождений и ремонта технологических пло-
щадок применяются прицепные, как пассивные (РКШ) так и активные (МТП-26)
корчеватели пней. При этом могут использоваться одиночные и групповые клыки,
навешиваемые на гусеничные тракторы. Для корчевки крупных пней используются
торфяные экскаваторы, оснащенные корчевальными крюками или специальными
захватами.
Валкование выкорчеванных пней производится машиной МП-3.
Погрузка осуществляется грейферными погрузчиками МТТ-12 или экска-
ватором МТП-71, однако наиболее производительной является погрузчик непре-
рывного действия МТП-29.
Вывозка пней к местам временного складирования за пределами осваивае-
мого месторождения - в транспортных тележках типа ГПС (МТП-24), агрегатируе-
мых с гусеничными тракторами кл.тяги 3, например, ДТ-75Б.
Для обработки малопнистых месторождений серийно выпускается МТП-26,
прицепная к гусеничному трактору кл.тяги 7 или 10, болотоходной модификации.
Рабочим органом является корчующий ротор с клыками, установленный
фронтально, валковый сепаратор пней и оформитель валка в виде двух наклон-
ных отвалов. Модификацией машины МТП-26 является МТП-81, которая обеспе-
чивает не только сплошную корчевку пней на глубину 0,4 м и сепарацию их от
торфа, но и с помощью скребкового конвейера одновременную погрузку в транс-
портную тележку.
При расчете нагрузок на рабочем органе корчевателя принимается усилие
корчевания на один клык Рк1≅5⋅106⋅d2, Н.
Комплексно операции по сплошной корчевке, сепарации и погрузке пней
и древесных включений в транспортные агрегаты обеспечивает самоходный
комбайн КУП.

а – вид сбоку; б – вид сверху; 1 – ходоуменьшитель; 2 – гидросистема; 3 – трансмиссия; 4 – гусеничная тележка; 5 – рама; 6, 7
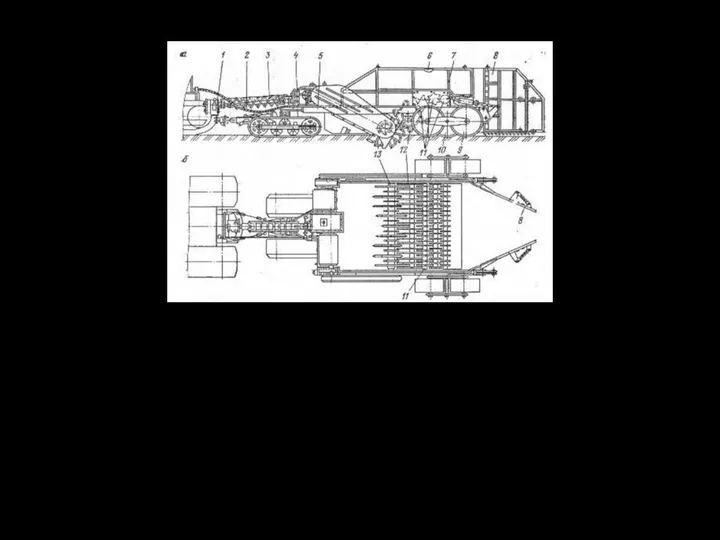
– борта; 8 – формователь валка; 9 – балансирная каретка; 10 – каток прикатывающий; 11 – транспортирующее-сеперирующие
роторы; 12 – съемный ротор; 13 – корчующий ротор
Рис. 6.7.1. Схема машины для сплошной корчевки пней МТП-26

1 – гидросистема; 2 – ходоуменьшитель; 3 – трансмиссия; 4, 11– гусеничные тележки; 5 – ограждение; 6 – рама; 7 – установка
щита; 8 – корчующий, съемный и транспортирующее-сепарирующие роторы; 9 – борта; 10 – погрузочный конвейер
Рис. 6.7.2. Схема корчевателя пней МТП81А

6.7.2 Мощность на работу машины МП-3 для валкования пней
1 ν 2
ω
Р1
Р2 Р
3
Рис. 6.7.3
Машина для валкования пней -
полунавесное оборудование с передним
опорным рояльным катком 2 на гусе-
ничном тракторе 3.
Рабочий орган – горизонтальный,
цилиндрический ротор с клыками 1
установлен под углом 54о относительно
продольной оси, вращается встречно
поступательному движению машины.
Параметры ротора:
-диаметр/длина, м 1,2/3,0
-высота клыков, мм 250
-количество клыков, шт 40
-частота вращения, с-1 8
Ширина захвата машины, м 2,5
Механический привод ротора
обеспечивается от заднего хвостовика
ВОМ через двухскоростной цилиндри-
ческий редуктор, два карданных теле-
скопических вала, неортоганальный ко-
нический редуктор и цепную передачу.
Необходимые затраты энергии для работы машины включают:
Мощность для передвижения гусеничного трактора
1
1 0
1 1000
( )
η
μmmgν
N=NГ=Г T+М ,
где μГ=μ1+μ2=0,12- коэффициент сопротивления движению гусеничного трактора;
mT – эксплуатационная масса трактора, кг;
m1М – часть массы оборудования, приходящаяся на движитель трактора, кг;
ν0 – кинематическая (теоретическая) скорость трактора, м/с.
Мощность на сообщение кинетической энергии отбрасываемым пням
2
2
2 .2000η
ρпxνK
кэ
Q
N=N= ,
где ρп – плотность неочищенных пней, кг/м3
Qx – производительность по ходу машины, м3/с;
υК - окружная скорость по концам клыков, м/с;
η1 и η2 – КПД трансмиссии трактора и привода ротора.
Мощность на преодоление сопротивления передвижению рояльного колеса
3 . 1000
μКKν
рк
G
N=N= ,
где GK – вертикальная нагрузка на рояльное колесо, Н;
ν=ν0(1-δ) – действительная скорость агрегата с учетом пробуксовки δ.

6.7.3 Клавишный сепаратор: производительность и затраты мощности
Производительность клавишного сепаратора характеризуется по двум состав-
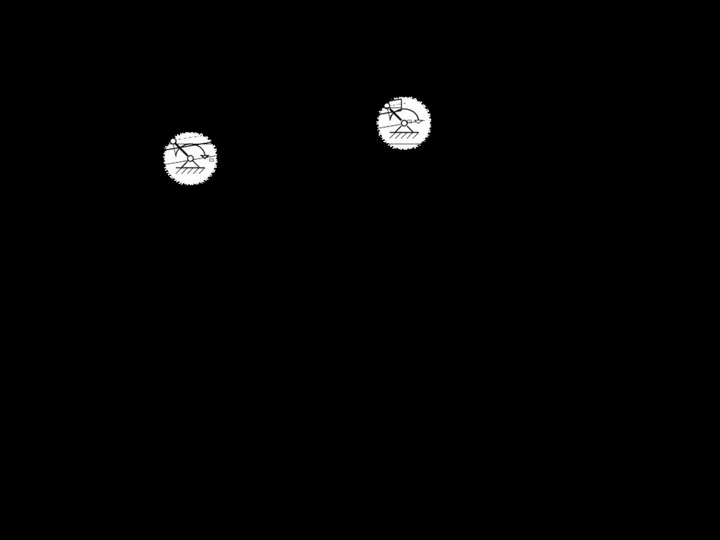
ляющим: по пням и по торфу.
В L пни
пни с торфом
bc Hc ω
торф e
е ω
Рис.6.7.4 Принципиальная схема клавишного сепаратора
Производительность сепаратора по торфу
t
V
Q kp
c.m=ϕm⋅ , м3/с
где ϕт – коэффициент заполнения рабочего пространства сепаратора торфом;
kp – коэффициент разрыхления массива торфа;
V=2еLB – объем рабочего пространства сепаратора, м3;
t=60/n=2π/ω - продолжительность одного цикла, с;
е – эксцентриситет коленчатого вала сепаратора, м;
L и B – рабочие длина и ширина сепаратора, м.
Производительность сепаратора по пням
t
V
Q kп
с.п=ϕп⋅ , м3/с
где ϕп ≅ 0.7 –коэффициент, учитывающий проскальзывание пней относительно кла-
виш сепаратора;
kn=ρт/ρп – заполнение пнями пространства над рабочей поверхностью;
ρт и ρп – плотность торфа и пней, кг/м3;
V=2ehBz - объем материала, проталкиваемого сепаратором за один оборот ко-
ленчатого вала, м3;
h – высота слоя материала над сепаратором, м;
z – число передвижек за один оборот коленвала.
Мощность для работы клавишного сепаратора включает:
Мощность на подбрасывание пней или сообщение кинетической энергии
п
к ncnк
кэ
Q
t
m
N
ηϕ
ν ρ ν
2
2
.
2
. 2 2000
= = ,
где νк=ωе – окружная скорость клавишей, м/с;
Мощность для подъема пней на высоту Hc
2
.
. 1000η
ρncn c
пэ
QgH
N= .
Мощность на прорезание торфа клавишами и на его трение о боковые поверхности клавиш
Nт.р=А/(1000tη2).

6.7.4 Мощность для уборки пней комбайном типа КУП
Комбайн КУП – самоходная ма-
шина для сплошной корчевки, сепара-
ции и погрузки пней и древесных вклю-
чений в транспортные агрегаты. В
рабочем режиме мощность двигателя 1
тратится на передвижение 2 комбайна, а
также на работу корчующего ротора 3,
сепаратора 4 и скребкового конвейера 5.
(G=mg – вес машины, Н)
Мощность на передвижение включает две составляющие:
2
0
1
. . 0
1000
(1 )
1000
( )
η
ν ε
η
μ + + ν+ −
NГ+Nn=ГGGnmPкZ Pn ,
где μГ – коэффициент сопротивления передвижению гусеничного хода 2;
Gп.т – вес выкорчеванного материала (пней с торфом) на рабочих органах, Н;
Рк.Z – вертикальная составляющая сопротивления корчевания, Н;
Рк.1≅10 кН – среднее усилие корчевания на один клык, Н;
Рп=0,3 Рк. – горизонтальная составляющая усилия подачи на роторе, Н.
Мощность на работу корчующего ротора включает затраты энергии на
непосредственное корчевание и подъем массы на определенную высоту:
2
.
2
. .1000 1000η
ρ
η
кωpp nm хp
кп nэ
P r gQH
N+N= + ,
где ωр и rр – угловая скорость (рад/с) и радиус ротора по концам клыков (м);
ρп.т =≅1000 кг/м3 – плотность пней с торфяной массой;
Qx=Fν=НкВкν - производительность по ходу, м3/с;
Нк и Вк – глубина корчевания и ширина захвата ротором, м;
ν=ν0(1-ε) – действительная, поступательная скорость машины, м/с;
Нр – высота подъема массы корчующим ротором, м.
Мощность на работу сепаратора (см.раздел 3.8.3) включает:
Nc=Nк.э.с+Nn.э.с+Nm.p.c,
где Nк.э.с - мощность на подбрасывание пней или сообщение кинетической энергии;
Nп.э.с - мощность для подъема пней на высоту Hc;
Nт.р.с - мощность на прорезание торфа клавишами и на его трение о боковые
поверхности клавиш.
Мощность для работы скребкового конвейера, т.е. мощность на волочение
пней скребками по желобу и на подъем пней до высоты погрузки:
4
.
.4
. 1000 1000
.
η
ρ
ηη
μρ ν n nск
ск
npnn к
ск
QL gQH
N= ск+ ,
где μпр= 0.3 – приведенный коэффициент сопротивления перемещению полотна кон-
вейера по направляющим;
Qn=αQx – производительность по пням, м3/с;
Lс.к – рабочая длина конвейера, м; νк – скорость полотна конвейера, м/с;
Нс.к=Нп-Нс - высота подъема пней скребковым конвейером, м;
η4 и ηс.к – КПД привода и самого конвейера.
ν
5
4
3
2
1
торф
пни
пни+тор
ф

6.7.5. Конструктивные особенности движителей тракторных прицепов
а, б, в – гусеничные прицепы: 1 и 2 переднее и заднее направляющее колеса;
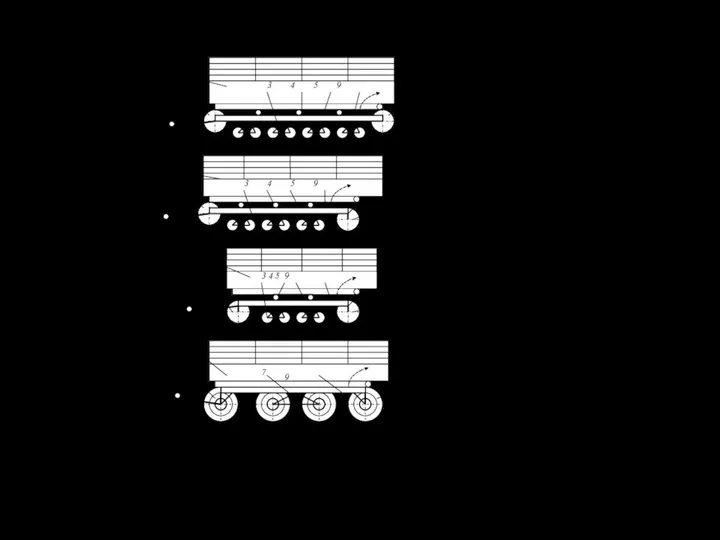
3 -опорные балансирные каретки; 4 поддерживающие ролики; 5 – гусеничная лента
г – колесный прицеп на арочных шинах: 6 – передняя управляемая ось; 7 – средняя
балансирная тележка; 8 – задняя ось;
9 – рама; 10 – дышло; 11 – кузов.
Рис. 6.7.5
б)
а)
а)
в)
г)
1
8
2
2
2
1
1
6
10
10
1
10
10
11
11
11
11
3 4 5 9
3 4 5 9
3 4 5 9
7 9

Таблица 6.7.5 - Технические данные тракторных прицепов серии МТП-24
№
п/п
Наименование парамет-
ра
Ед.
изм МТП-24А МТП-24Б МТП-24В МТП-24К
1. Тип движителя г у с е н и ч н ы й колесный
2. Агрегатирование Гусеничные тракторы кл.тяги 3
3. Масса: кг 7850 6500 5800
4. Грузоподъемность кг 9000 9000 9000
5. Габариты (с наращенными бортами)
- длина (без прицепного) мм 5580 4800
- ширина мм 3730 3500
- высота мм 2520 2600
6. Внутр.размеры кузова:
- длина мм 5120
- ширина мм 2710
- высота мм 500
7. Объем кузова:
- без наращ. бортов м3 6.5 6.0 6.0
- с наращ. бортами м3 22 20 20.0
8. Движитель (пассив-
ный):
Металлические звенчатые об-
водные ленты; опорные балан-
сирные каретки
Арочные
шины
(Я-170)
- ширина гусеницы;
- параметры шины
мм 750 750 750 D=1150;
B=700мм
- количество шт 2 2 2 4х2=8
- колея мм 2000 2000 2000
- продольная база мм 4610
- длина опорной части мм 3423 3830 3030 -
10. Скорость движения км/ч до 10
11. Переоборудование
движителя
Полозья санные: количество -2;
Масса 1120кг; ширина 650мм;
полная/опорная длина 4370/3370
-
12. Массы осн. сб.единиц: Масса
одной
шины с
колесом
170 кг
- гусеничные ленты кг
- подвеска балансирная кг 440х4
- колесо натяжное кг 127х2
- колесо отклоняющее кг 63х2
- каток поддерживающ. кг 29х2 29х6
- рама кг 940
- кузов кг 1105
- борт передн.+наращ.б. кг 60+87
- дополн. борт (лев.+пр) кг 133+133
- дышло кг 96
- гидрооборудование кг 152
в т.ч. гидроцилиндры кг 64х2
РАЗРАБОТЧИК и ИЗГОТОВИТЕЛЬ:
гусеничные прицепы (серийно) - Нелидовский завод торфяного машиностроения;
прицеп на арочных шинах (опытные образцы) – «БелНИИтопроект».

3.7.6 Выбор параметров гидропривода
для опрокидывания кузова тракторного прицепа
На вывозке древесины и пней, а также для доставки технологических материа-
лов в пределах торфяного месторождения широкое распространение получили само-
разгружающиеся гусеничные прицепы МТП-24, агрегатируемые с гусеничными
тракторами кл.тяги 3 (Таблица 3.8). В частности, прицеп МТП-24Б предназначен для
работы с трактором ДТ-75Б. При конструктивной массе прицепа (с наращенными
бортами) тП=6500 кг геометрическая вместимость кузова VK=20м3, а грузоподъем-
ность тГ=9000 кг. Параметры гусеничного хода: ширина гусеничных лент b=750 мм,
длина опорной части (между осями передних опорных катков и задних направляю-
щих колес) L=3830 мм. Среднее давление в пятне контакта гусениц с опорным осно-
ванием при полной загрузке
27 .
21000
( )
кПа
bL
ттg
p П Г≅
⋅
+
=
Рис.6.7.6
Опрокидывание кузова с грузом назад происходит относительно задних шар-
ниров A с помощью двух спаренных телескопических гидроцилиндров (n=2), уста-
новленных наклонно α0 между рамой гусеничного хода В(lB;hB) и днищем С(lC;hC), и
подключенных к гидросистеме трактора (Рис.3.8.6).
Усилие РЦ на штоке гидроцилиндра, минимально достаточное для обеспечения
опрокидывания, определяется из условия равновесия моментов от действующих сил
относительно оси шарнира А, т.е. ΣМА = 0,
Ц
K Г
Ц nH
GhGh
P
⋅
⋅+ ⋅
= 1 2, Н
где GК=(тк+тб)g – вес кузова с наращенными бортами; GГ=ρмVм g – вес груза, Н;
ρм и Vм – насыпная плотность (кг/м3) и объем (м3) материала в кузове;
НЦ, h1 и h2 – плечи действия сил РЦ, GК и GГ относительно точки А, м.
РЦ
GГ
HЦ
h1
h2
α0
lB
L
GK
В A hВ
С
О2
О1
hC
lC

Б - гидробак
Н – насос шестеренный НШ-46
Р – распределитель Р-75:
3-х секционный (СР1, СР2, СР3),
4-х канальный, 4-х позиционный;
Ц1, Ц2 - гидроцилиндры :
телескопические, двухсекционные
(Dn.н/Dп.в=120/100мм; Lх.ш=1,5м)
АТ – аппарат теплообменный
Ф - фильтр
М - манометр
1 – гибкий трубопровод
2 – муфта
быстроразъемная ;
3 – клапан сдвоенный
(переливной);
4 – клапан
предохранительный
5, 6, 7 – рукоятки
управления
Рис. 6.7.7 - Принципиальная гидравлическая схема
гидропривода для опрокидывания кузова тележки МТП-24
СР1 СР2 СР3
Ц2
Ц1
Р
Б
М
АТ
5
Н
4
3
2
1
6 7
Ф

6.8 ТОРФЯНОЙ ШНЕКОВЫЙ ПРОФИЛИРОВЩИК
6.8.1 Особенности конструкции торфяных шнековых профилировщиков
Торфяной шнековый профилировщик МТП-52 (ТПШ-2) работает в прицепе с гусе-
ничным, болотоходным трактором ДТ-75Б (с ходоуменшителем) кл.тяги 3. Рабочий орган –
фронтальная, цилиндрическая, однозаходная шнек-фреза общей длиной 6,5 м и диаметром
по режущим кромкам 800 мм в зоне разгрузки имеет коническую часть длиной 800 мм и
меньшим диаметром 400 мм. Она подвешена в полуцилиндрическом кожухе посредством
двух самоустанавливающихся подшипниковых опор со сферическими втулками. Привод –
от ВОМ трактора.
При поступательном движении машинно-тракторного агрегата и попутном вращении
шнек-фрезы происходит срезание верхнего слоя залежи под заданным углом и перемещение
его к середине карты. Поперечный наклон шнек-фрезы по отношению к горизонту, незави-
симо от положения ходовых колес,(опорных катков) поддерживается автоматически
(Рис.3.9), а необходимая величина уклона устанавливается заранее на жесткой площадке.
Следящим устройством при задании определенного уклона служит маятник, управляю-
щий механизмом подъема-опускания рабочего органа.
1 – шнек-фреза; 2 – кожух; 3 и 4 – гидроцилиндры; 5 – рама профилировщика;
6 и 7 – опорные катки; 8 – маятник управляющий; 9 – бак с жидкостью;
10 – гидросистема трактора; 11 и 12 – трехпозиционные распределители
Рис. 3.9 Схема автоматической системы поддержания заданного положения шнек-
фрезы по отношению к горизонту
Рис. 6.8.1
8 9
6 7
1
5
3 4
2
1
10
11 12

а – вид сбоку; б – вид сверху (повернуто);
Рис. 6.8.2. Шнековый профилировщик МТП-52

6.8.2 Мощность для работы шнекового профилировщика
Затраты мощности зависят от того, какая операция выполняется машиной.
Если осуществляется 1-й проход от края картовой канавы к ее середине, а со-
ответственно, только снятие слоя торфа, то суммарные затраты мощности для ра-
боты шнекового профилировщика включают пять составляющих:
N=NТ+NМ+Nф.т+Nф.п+Nтр , кВт.
Мощность для передвижения гусеничного трактора и колесного прицепа
(профилировщика):
1000
(1 )
1000
0
1
0μ ν ε
η
μ ν+ −
NТ+NМ= гmTg кmMg ,
где тТ и тМ – эксплуатационные массы трактора и профилировщика, кг;
μг и μк – коэф.-ты сопротивления движению гусеничного и колесного хода;
υо – кинематическая (теоретическая), поступательная скорость агрегата, м/с;
ε - буксование гусеничного движителя.
Мощность на фрезерование торфа N3 и пня N4:
2 2
. . 1000 1000
(1 )
η
α
η
αтх пx
фт фп
pQ pQ
N+N=− + ,
где pm=20000δ - удельные затраты энергии на фрезерование торфа, Н/м2;
δ=2πν/ω - толщина стружки, м;
рп=(70…100)рт - удельные затраты энергии на фрезерование пня, Н/м2;
Qx=Fν=0,5hmaxBν - производительность по ходу машины, м3/с;
η1 и η2 – КПД трансмиссии трактора и привода шнек-фрезы.
При расчете Qx следует учитывать, что толщина снимаемого слоя h по ширине захва-
та В изменяется от 0 до hmax.
Мощность на транспортирование шнеком сфрезерованной массы:
тр о
S
N
21000360
1
2
β
η
τω
= ⋅ ⋅ ,
где τ=5000 Н/м2 – предельное напряжение сдвига свежесфрезерованного торфа;
ω = частота вращения шнек-фрезы, с-1;
S=FкR=2πR2l - статический момент внутренней поверхности кожуха шнека
относительно оси вращения для случая, когда кожух полностью (360о) охватывал бы
шнек-фрезу;
β - конструктивный угол охвата кожухом шнек-фрезы.
При последующих проходах агрегата к середине карты происходит, в основ-
ном, фрезерование и дальнейшее транспортирование ранее накопленной массы,
поэтому вместо составляющих Nф.т и Nф.п следует учитывать только затраты мощно-
сти на фрезерование свеженасыпанного материала:
2
. .
.1000η
ст ix
ст
pQ
N= ,
где рс.т=(0,5…0,7)рт–удельные затраты энергии на фрезерование свеженасыпанного
торфа;
Qi.x – производительность профилировщика при последующих проходах.

ВСПОМОГАТЕЛЬНЫЙ РАЗДЕЛ
ТИТУЛЬНЫЕ ЛИСТЫ
основной литературы
по дисциплине
«Горные машины и оборудование»

УДК 622.363.2 (075.8)
Горные машины для калийных рудников / А.Б. Морев, А.Д. Смычник,
Г.В. Казаченко. –Минск: Интегралполиграф, 2009, - 544 с.
Табл. 5. илл. 201. Библ. 25 назв.
ISBN 978-9856845-16-4.
В монографии приведен краткий обзор сырьевой и производственной базы калийной отрасли Беларуси,
описаны технологические схемы выемки. Изложены принцип действия и особенности конструкций горных
машин для выемки соляных пластов и подготовки выемочных участков. Приведены основные требования без-
опасности горного оборудования.
Книга предназначена для работников калийной промышленности, а также преподавателей, аспирантов и
студентов специальности горного профиля.

УДК 622.232.83
ББК 33.345
У82
ISBN 978-985-458-201-6
Устройство и эксплуатация проходческого комбайна ПКС-8М / В.А. Дани-
лов, И.А. Конопляник, П.А. Дворник, А.Н. Леончик, В.Д. Михаленя, В.Я. Пру-
шак, В.Я. Щерба. Под ред. В.Я. Прушака – Минск : Тэхналогiя, 2010. -175 с.
В книге рассмотрены конструкция и принцип работы механической, гидравлической и электрической частей, систем
управления и обеспечения работоспособности проходческого комбайна ПКС-8М производства ЗАО «Солигорский институт
проблем ресурсосбережения с опытным производством». Приведены основные технические характеристики комбайна. Да-
ны рекомендации по настройке и регулировке его узлов и систем, по управлению комбайном при выполнении типовых
операций, указания по мерам безопасности, монтажу, подготовке к работе, обкатке, техническому обслуживанию и ремонту
комбайна. Приведены характерные неисправности и рекомендации по их устранению. Изложены методики испытаний ком-
байна.
Книга предназначена для технического персонала, выполняющего монтаж и демонтаж, эксплуатацию, техническое об-
служивание и ремонт комбайна. Она может быть полезна учащимся учреждений профессионального и среднего образова-
ния, студентам вузов соответствующих специальностей.

Министерство образования
Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Горные машины»
Г.В. Казаченко
Г.А. Басалай
Э.А. Кремчеев
КОЛЕСНЫЕ ДВИЖИТЕЛИ ГОРНЫХ МАШИН
Методическое пособие
Минск
БНТУ
2012
УДК 622.002.5.004
ББК 33.16я7
К 14
К 14
Казаченко, Г.В.
Колесные движители горных машин: методическое пособие по дисци-
плинам «Горные машины и оборудование» и «Проектирование техники
для подземных горных работ» / Г.В. Казаченко, Г.А. Басалай,
Н.В. Кислов. – Минск: БНТУ, 2012. – 34 с.
ISBN 979-985-525-814-9.
В издании рассмотрены примеры статического расчета колесных машин, используемых при подземной разра-
ботке калийных месторождений. Пособие может быть использовано при узучении дисциплин «Горные машины и
оборудование», «Проектирование техники для подземных горных работ».
УДК 622.002.5.004 (075.8)
ББК 33.16я7
ISBN 979-985-525-814-9 © Казаченко Г.В., Басалай Г.А.,
Кремчеев Э.А. 2012
© БНТУ, 2012
Содержание: смотри файл «Колесные движители горных машин»

2. ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1 ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
1. Статический расчет горной машины на гусеничном ходе.
2. Тяговый расчет горной гусеничной машины.
3. Расчет устойчивости экскаватора.
4. Определение производительности очистного комбайна и баланс его мощно-
сти.
5. Расчет мощности приводов механизмов проходческого комбайна.
6. Определение теоретической скорости проходки.
7. Определение мощности механизмов щеленарезной машины.
8. Расчет тяговых нагрузок забойного конвейера.

Министерство образования Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
_________________________________________________________
______
КАФЕДРА «ГОРНЫЕ МАШИНЫ»
Г.В КАЗАЧЕНКО, Н.В. КИСЛОВ
СТАТИЧЕСКИЙ И ТЯГОВЫЙ РАСЧЕТ
ГОРНОЙ ГУСЕНИЧНОЙ МАШИНЫ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
к практическим занятиям
по курсу «Машины и комплексы открытых горных работ»
для студентов специальности 36 10 01
«Горные машины и оборудование»
Минск 2002
УДК 622.331.002
Методическое пособие к практическим занятиям по горным машинам предназначено для студентов специальности 36
10 01 «Горные машины и оборудование».
В пособии изложены теоретические основы и методики статического и тягового расче-
тов мобильной горной машины на гусеничном ходу. Методики реализованы в виде программ
для ПЭВМ.
Георгий Васильевич КАЗАЧЕНКО
Николай Владимирович КИСЛОВ
© Казаченко Г.В., Кислов Н.В., 2002
Содержание: смотри файл «СТАТИЧЕСКИЙ И ТЯГОВЫЙ РАСЧЕТ»

Министерство образования
Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Горные машины»
Г.В. Казаченко
Н.В. Кислов
Г.А. Басалай
ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ ОЧИСТНОГО
И ПРОХОДЧЕСКОГО КОМБАЙНОВ
Методическое пособие
Минск
БНТУ
2012
УДК 622.002.5.004 (075.8)
ББК 33.16я7
К 14
К 14
Казаченко, Г.В.
Энергетический расчет очистного и проходческого комбайнов: мето-
дическое пособие по дисциплинам «Горные машины и оборудование» и
«Проектирование техники для подземных горных работ» / Г.В. Казаченко,
Н.В. Кислов, Г.А. Басалай. – Минск: БНТУ, 2012. – 38 с.
ISBN 979-985-525-814-9.
В издании рассмотрены примеры энергетического расчета очистного и проходческого комбайнов, используе-
мых при подземной разработке калийных месторождений. Пособие может быть использовано при узучении дисци-
плин «Горные машины и оборудование», «Проектирование техники для подземных горных работ».
УДК 622.002.5.004 (075.8)
ББК 33.16я7
ISBN 979-985-525-814-9 © Казаченко Г.В., Кислов Н.В.,
Басалай Г.А., 2012
Содержание: смотри файл «ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ
ОЧИСТНОГО И ПРОХОДЧЕСКОГО КОМБАЙНОВ»

2.2 ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ ЛАБОРАТОРНЫХ РАБОТ
1. Комплекс средств выполнения лабораторных работ на грунтовом канале.
2. Градуировка средств измерений.
3. Напряжения и деформации опорного основания под ходовыми устройства-
ми.
4. Коэффициент трения между гусеничным траком и опорным основанием.
5. Коэффициент сопротивления движению колеса по деформируемому основа-
нию.
6. Удельное сопротивление резанию горной породы пассивным резцом.
7. Комбинированный исполнительный орган проходческого комбайна серии
ПК.
8. Планетарный исполнительный орган проходческо-очистного комбайна
УРАЛ.
9. Конструктивные особенности гусеничного хода проходческого комбайна.
10. Колесный движитель шахтного самоходного вагона 5ВС-15М.
11. Очистные комбайны для подземных разработок полезного ископаемого ла-
вами.
12. Определение характеристик секций механизированных крепей

Министерство образования Республики Беларусь
Белорусский национальный технический университет
Кафедра «Горные машины»
Г.В. Казаченко,
Г.А. Басалай,
Г.И. Лютко
Лабораторные работы
по дисциплине
«Горные машины и оборудование»
Часть 1. Взаимодействие рабочих органов
машин с горными породами
Минск 2009
УДК 622.002
ББК
Рецензенты: П.В. Цыбуленко, А.А. Кологривко
В пособии описаны лабораторные установки и оборудование, а также методика выполнения лабораторных
работ, описаны средства регистрации и обработки опытных данных. Изложены правила безопасной эксплуата-
ции оборудования, порядок выполнения лабораторных работ и оформления отчетов.
Содержание: смотри файл «Лабораторные работы. Часть 1».
Py
Pz
l2 l1
Pс
α
G h Pд
О
АЦП ПЭВМ

Министерство образования Республики Беларусь
Белорусский национальный технический университет
Кафедра «Горные машины»
ГОРНЫЕ МАШИНЫ И ОБОРУДОВАНИЕ
Лабораторные работы
в 2 частях
Часть 2. Анализ параметров горных машин
Минск, БНТУ, 2011
УДК 622.002.5.004 (075.8)
ББК 33.16я7
Г69
Составители:
Г.А. Басалай, Г.В. Казаченко, Г.И. Лютко
Г69 Горные машины и оборудование: лабораторные работы: в 2 ч./ сост.: Г.А. Басалай, Г.В. Казаченко, Г.И. Лютко. –
Минск: БНТУ, 2011. – Ч.2: Анализ параметров горных машин. - с.
В издании описаны лабораторные установки и оборудование, а также методика выполнения лабораторных работ, сред-
ства регистрации и методы обработки опытных данных. Изложены правила безопасной эксплуатации оборудования, поря-
док выполнения лабораторных работ и оформления отчетов.
Часть 1 «Взаимодействие рабочих органов машин с горными породами» вышла в свет в 2010 г. в
БНТУ.
ISBN 979-985-525-590-2 (ч.2) БНТУ, 2011290-1
Содержание: смотри файл «Лабораторные работы. Часть 2».

УЧЕБНАЯ ПРОГРАММА
по дисциплине
«Горные машины и оборудование»

УТВЕРЖДАЮ
Проректор по учебной, воспитательной
аналитической и информационной
работе
________________ Г.Ф. Ловшенко
15.10.2011
Регистрационный № УД-ФГДЭ 20-41/баз.
ГОРНЫЕ МАШИНЫ И ОБОРУДОВАНИЕ
Учебная программа дисциплины для специальности
1-36 10 01 «Горные машины и оборудование»
по направлению 1-36 10 01-02 «Горные машины и оборудование
(подземные разработки)»
Минск 2011 г.

СОСТАВИТЕЛИ:
Н.В. Кислов, профессор кафедры «Горные машины» Белорусского националь-
ного технического университета, доктор технических наук, профессор
Г.В. Казаченко, доцент кафедры «Горные машины» Белорусского националь-
ного технического университета, кандидат технических наук, доцент
РЕЦЕНЗЕНТЫ:
В.А. Сорокин, начальник отдела технической диагностики, испытаний и сер-
тификации горно-шахтного оборудования Открытого акционерного общества
«Белгорхимпром», старший научный сотрудник, кандидат технических наук;
А.А. Кологривко, доцент кафедры «Горные работы» Белорусского националь-
ного технического университета, кандидат технических наук, доцент;
РЕКОМЕНДОВАНА К УТВЕРЖДЕНИЮ:
Кафедрой «Горные машины» Белорусского национального технического
университета
(протокол от 22.04.2011 № 10)
Заведующий кафедрой Н.И. Березовский
Методической комиссией факультета горного дела и инженерной экологии
Белорусского национального технического университета
(протокол от 10.05.2011 № 12)
Председатель методической
комиссии С.Г. Оника
Ответственные за редакцию Н.В. Кислов
Г.В. Казаченко

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебная программа дисциплины «Горные машины и оборудование»
предназначена для специальности 1-36 10 01 «Горные машины и оборудова-
ние» по направлению 1-36 10 01-02 «Горные машины и оборудование (под-
земные разработки)» высших учебных заведений.
Программа предусматривает изучение конструкций горных машин и
расчетов их основных параметров. Основная задача при изучении курса – по-
лучение студентами знаний, необходимых для расчетов, конструирования и
правильной эксплуатации машин, обеспечивающих комплексную механиза-
цию процессов добычи и первичной переработки полезных ископаемых.
Освоение дисциплины предполагает также выработку навыков применения
полученных знаний для технического анализа конкретных машин и синтеза
их более совершенных вариантов.
Дисциплина базируется на курсах: математика, физика, теоретическая
механика, сопротивление материалов, теория механизмов и машин, детали
машин, физико-механические свойства и разрушение горных пород,
численные методы в горном деле, гидромеханический привод горных машин.
В результате освоения курса «Горные машины и оборудование»
студент должен:
знать:
- структуру и классификацию горных машин, комплексов и
технологического оборудования;
- принципы действия и конструктивные схемы машин и оборудования;
- теоретические основы расчетов машин и их рабочих органов;
уметь:
- составлять расчетные схемы и определять нагрузки, действующие на раз-
личные звенья;
- вычислять конструктивные и режимные характеристики рабочих процес-
сов;
- оценивать эти параметры с точки зрения их рациональности и оптимально-
сти;
приобрести навыки:
- выполнения расчетов устойчивости машин;
- анализа конструктивных схем и определения затрат мощности на работу
отдельных механизмов.
Методы обучения
При изучении дисциплины используются как традиционные, так и совре-
менные методы и технологии обучения:
− изложение теоретических основ на лекционных занятиях;
− определение характеристик машин и процессов добычи полезных ис-
копаемых на лабораторных занятиях;
− выполнение расчетов на практических занятиях;
− проведение расчетов и выполнение чертежей с использованием ком-

пьютерных технологий в курсовом проектировании.
Организация самостоятельной работы студентов Самостоятельная работа студентов охватывает все виды занятий и за-
ключается в подготовке к ним, и реализуется при выполнении курсового
проекта. В курсовом проекте студенты самостоятельно анализируют кон-
струкции основных горных машин, делают свои технические предложения,
производят необходимые расчеты и анализируют технические параметры.
Диагностика компетенций студента
Оценка компетенций студентов производится следующими способами:
– текущим контролем знаний отдельных вопросов во время проведения
всех видов учебных занятий;
− защитой отчетов по лабораторным и практическим занятиям;
– зачетом в конце семестра;
− защитой курсового проекта;
− сдачей экзаменов.
Изучение дисциплины «Горные машины и оборудование» рассчитано
на 290 часов, в том числе — 142 часа аудиторных занятий.
Примерное распределение аудиторных занятий по их видам в соответ-
ствии с типовым учебным планом следующее:
лекции — 64 часа;
практические занятия — 46 часов;
лабораторные занятия — 32 часа.
Примерный тематический план
Наименование раздела и темы
Лекции (часы)
Практические заня-
тия (часы)
Лабораторные заня-
тия (часы)
Всего аудиторных
часов
1 2 3 4 5
Раздел I. Введение
Тема 1. Краткая история развития машин и комплексов для
горных работ. Классификация
2
Раздел II. Структура горных машин. Общие расчеты
Тема 2. Общая структура современных горных машин. Ос-
новные законы сохранения и балансовые соотношения
2 2
Тема 3. Статический расчет горных машин 4 8 8
Раздел III. Исполнительные органы горных машин

1 2 3 4 5
Тема 4. Классификация исполнительных органов. Бара-
банные, шнековые, дисковые, цепные, дисковые, коронча-
тые и планетарные органы выемочных машин
2
Тема 5. Кинематика движения элементов разрушения и
удельные затраты мощности
8 6 4
Тема 6. Погрузочные органы горных машин 2
Раздел IV. Механизмы перемещения и подачи
Тема 7. Гусеничные движители и их расчет 6 4 6
Тема 8. Колесный ход 4 2 3
Тема 9. Шагающие механизмы перемещения 2
Раздел V. Комплексы для подземных горных работ
Тема 10. Проходческие и очистные комбайны 8 10 8
Тема 11. Механизированные крепи 4 4
Тема 12. Забойные конвейеры 2 4
Раздел VI. Машины и комплексы для открытых гор-
ных работ
Тема 13. Классификация машин и основные схемы работ 2
Тема 14. Экскаваторы и мощность для работы основных
механизмов
6 8
Тема 15. Машины для добычи торфа 6 4
Раздел VII. Буровое оборудование
Тема 16. Общие сведения и способы бурения 2
Тема 17. Конструктивные схемы и расчет процессов буре-
ния
2
ВСЕГО 64 46 32 142
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Раздел I. ВВЕДЕНИЕ
Тема 1. КРАТКАЯ ИСТОРИЯ РАЗВИТИЯ МАШИН И КОМПЛЕКСОВ
ДЛЯ ГОРНЫХ РАБОТ. КЛАССИФИКАЦИЯ
Цель и задачи изучения курса, краткое содержание. Основные этапы
развития горных машин и оборудования. Области применения и общая клас-
сификация.
Раздел II. СТРУКТУРА ГОРНЫХ МАШИН. ОБЩИЕ РАСЧЕТЫ
Тема 2. ОБЩАЯ СТРУКТУРА СОВРЕМЕННЫХ ГОРНЫХ МАШИН.
ОСНОВНЫЕ ЗАКОНЫ СОХРАНЕНИЯ И БАЛАНСОВЫЕ СООТНОШЕНИЯ
Основные структурные элементы горных машин, их связи. Балансовые
соотношения по производительности и мощности. Задачи, для решения кото-
рых используются балансовые соотношения.

Тема 3. СТАТИЧЕСКИЙ РАСЧЕТ ГОРНЫХ МАШИН
Определение центра масс машины. Внешние нагрузки, действующие
на машину. Пространственная ориентация машин. Понятие центра давления
и распределение давления машины на опорное основание и его деформации.
Раздел III. ИСПОЛНИТЕЛЬНЫЕ ОРГАНЫ ГОРНЫХ МАШИН
Тема 4. КЛАССИФИКАЦИЯ ИСПОЛНИТЕЛЬНЫХ ОРГАНОВ.
БАРАБАННЫЕ, ШНЕКОВЫЕ, ДИСКОВЫЕ, ЦЕПНЫЕ,
ДИСКОВЫЕ, КОРОНЧАТЫЕ И ПЛАНЕТАРНЫЕ ОРГАНЫ
ВЫЕМОЧНЫХ МАШИН
Назначение исполнительных органов и их классификация. Основные
типы механизмов разрушения. Барабанные, шнековые, дисковые, цепные ме-
ханизмы. Буровые, корончатые, планетарные и струговые органы разруше-
ния.
Тема 5. КИНЕМАТИКА ДВИЖЕНИЯ ЭЛЕМЕНТОВ РАЗРУШЕНИЯ И
УДЕЛЬНЫЕ ЗАТРАТЫ МОЩНОСТИ
Способы разрушения горных пород и принципиальные схемы воздей-
ствия на массив. Механическое разрушение – основной способ выемки. Резец
и силы, действующие на него. Удельные затраты мощности и влияние на них
различных факторов. Толщина стружки при работе основных органов разру-
шения и ее влияние на удельные затраты мощности.
Тема 6. ПОГРУЗОЧНЫЕ ОРГАНЫ ГОРНЫХ МАШИН
Необходимость применения погрузочных устройств в выемочных
машинах. Совмещение погрузки и разрушения в исполнительных органах.
Конструктивные схемы и определение затрат мощности.
Раздел IV. МЕХАНИЗМЫ ПЕРЕМЕЩЕНИЯ И ПОДАЧИ
Тема 7. ГУСЕНИЧНЫЕ ДВИЖИТЕЛИ И ИХ РАСЧЕТ
Схема гусеничного движителя. Кинематика гусеничного обвода. Дей-
ствительная и теоретическая скорости, буксование. Мощность для движения
по прямой, мощность и условия возможности движения. Поворот гусенично-
го движителя. Уравнения равновесия и их решение. Кинематика поворота и
мощность для его выполнения.
Тема 8. КОЛЕСНЫЙ ХОД
Область применения. Кинематика колеса и его основные параметры.
Определение основных размеров. Мощность для передвижения и условия
возможности движения. Схемы поворота колесных движителей и кинемати-
ческие характеристики поворота. Особенности железнодорожных механиз-
мов передвижения.

Тема 9. ШАГАЮЩИЕ МЕХАНИЗМЫ ПЕРЕМЕЩЕНИЯ
Конструктивные схемы механизмов передвижения шагающих экскава-
торов, мощность для их работы.
Раздел V. КОМПЛЕКСЫ ДЛЯ ПОДЗЕМНЫХ ГОРНЫХ РАБОТ
Тема 10. ПРОХОДЧЕСКИЕ И ОЧИСТНЫЕ КОМБАЙНЫ
Проходческие и очистные комбайны и комплексы на их основе. Обла-
сти применения. Основные типы проходческих машин. Проходческие ком-
байны бурового типа. Мощности для их работы. Проходческие комбайны с
планетарно-дисковыми исполнительными органами. Мощность для их рабо-
ты. Определение усилия подачи. Самоходные вагоны. Очистные комбайны.
Основные зависимости для определения нагрузок и мощности. Механизмы
подачи очистных комбайнов.
Тема 11. МЕХАНИЗИРОВАННЫЕ КРЕПИ
Способы крепления горных выработок. Применение гидромеханизиро-
ванных крепей. Типы крепей и их конструктивные схемы. Выбор крепей в
зависимости от горно-геологических условий.
Тема 12. ЗАБОЙНЫЕ КОНВЕЙЕРЫ
Конструктивные схемы и назначение. Определение нагрузок и расчет
затрат мощности. Особенности работы конвейера в составе очистного ком-
плекса и учет изменения передвигаемой горной массы.
Раздел VI. МАШИНЫ И КОМПЛЕКСЫ ДЛЯ ОТКРЫТЫХ
ГОРНЫХ РАБОТ
Тема 13. КЛАССИФИКАЦИЯ МАШИН И ОСНОВНЫЕ СХЕМЫ РАБОТ
Карьер и его основные элементы. Способы добычи и применяемое
оборудование. Выемочно-погрузочные и транспортирующие машины.
Тема 14. ЭКСКАВАТОРЫ И МОЩНОСТЬ ДЛЯ РАБОТЫ
ОСНОВНЫХ МЕХАНИЗМОВ
Классификация экскаваторов. Конструктивные схемы одноковшовых и
многоковшовых экскаваторов. Мощность для приводов механизмов тяги, по-
ворота платформы и напора.
Тема 15. МАШИНЫ ДЛЯ ДОБЫЧИ ТОРФА
Машины для добычи торфа. Технологии и оборудование добычи. Ос-
новные операции фрезерного способа добычи и комплексы машин. Фрезеры
и определение мощности для их работы. Ворошилки и валкователи. Скре-
перно-бункерные уборочные машины. Машины для создания складочных
единиц. Пневмоуборочные машины и особенности их расчета.

Раздел VII. БУРОВОЕ ОБОРУДОВАНИЕ
Тема 16. ОБЩИЕ СВЕДЕНИЯ И СПОСОБЫ БУРЕНИЯ
Способы бурения и расчет процессов. Способы бурения: ударный,
ударно-вращательный, вращательный и вращательно-ударный.
Тема 17. КОНСТРУКТИВНЫЕ СХЕМЫ И РАСЧЕТ ПРОЦЕССОВ БУРЕНИЯ
Основные составные части буровой установки. Расчет процесса бурения.
Условия нормальной работы буровой установки.
ИНФОРМАЦИОННО-МЕТОДИЧЕСКАЯ ЧАСТЬ
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
9. Статический расчет горной машины на гусеничном ходе.
10. Тяговый расчет горной гусеничной машины.
11. Расчет устойчивости экскаватора.
12. Определение производительности очистного комбайна и баланс его мощ-
ности.
13. Расчет мощности приводов механизмов проходческого комбайна.
14. Определение теоретической скорости проходки.
15. Определение мощности механизмов щеленарезной машины.
16. Расчет тяговых нагрузок забойного конвейера.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ ЛАБОРАТОРНЫХ РАБОТ
13. Комплекс средств выполнения лабораторных работ на грунтовом канале.
14. Градуировка средств измерений.
15. Напряжения и деформации опорного основания под ходовыми устрой-
ствами.
16. Коэффициент трения между гусеничным траком и опорным основанием.
17. Коэффициент сопротивления движению колеса по деформируемому осно-
ванию.
18. Удельное сопротивление резанию горной породы пассивным резцом.
19. Комбинированный исполнительный орган проходческого комбайна серии
ПК.
20. Планетарный исполнительный орган проходческо-очистного комбайна
УРАЛ.
21. Конструктивные особенности гусеничного хода проходческого комбайна.
22. Колесный движитель шахтного самоходного вагона 5ВС-15М.
23. Очистные комбайны для подземных разработок полезного ископаемого
лавами.
24. Определение характеристик секций механизированных крепей

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ КУРСОВОГО ПРОЕКТА
Цель курсового проекта – научить студента навыкам инженерного про-
ектирования машин и комплексов для проведения горных работ и добычи
полезных ископаемых.
Курсовой проект включает чертежи общего вида машины с кинемати-
ческой и гидравлической схемами (3-4 листа формата А1) и пояснительную
записку, которая содержит общий расчет машины.
Тематика курсового проектирования включает разработку конструкции
машин для выполнения буровых работ, экскавации и погрузки твёрдой гор-
ной породы, проведения транспортных мероприятий, добычи, транспортиро-
вания, первичной переработки и складирования горной породы.
ОСНОВНАЯ ЛИТЕРАТУРА
2. Красников, Ю.Д. Горные машины / Ю.Д. Красников, В.Я. Прушак, В.Я.
Щерба. - Минск: Выш. шк., 2003.- 148 с.
3. Смычник, А.Д. Технология и механизация горных работ на калийных
рудниках Беларуси / А.Д. Смычник, А.Б. Морев. - Минск: УП Техно-
принт, 2002. - 200 с.
4. Гетопанов, В.Н. Горные и транспортные машины и комплексы / В.Н. Ге-
топанов, Н.С. Гудилин, Л.И. Чугреев. - М.: Недра, 1991.- 303 с.
5. Казаченко, Г.В. Статический и тяговый расчет горной гусеничной маши-
ны / Г.В. Казаченко, Н.В. Кислов. - Мн.: БНТУ, 2005. - 55 с.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1 Калугин, П.А. Горные машины фирмы «Айкхофф» на калийных рудниках
Беларуси / А.П. Калугин, А.Б. Морев. - Мн., 1993. - 110 с.
2 Солод, В.И. Проектирование и конструирование горных машин и ком-
плексов / В.И. Солод, В.Н. Гетопанов, В.М. Рачек. – М.: Недра, 1982. –
350 с.
3 Опейко, Ф.А. Торфяные машины Ф.А. Опейко. – Мн.: Вышэйшая школа,
1968. – 408 с.
4 Морев, А.Б. Горные машины для калийных рудников / А.Б. Морев,
А.Д. Смычник, Г.В. Казаченко. – Минск: Интегралколиграф, 2009. – 544
с.
5 Солод, В.И. Горные машины и комплексы / В.И. Солод. – М.: Недра,
1981. – 509 с.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
по дисциплине
«Горные машины и оборудование»

Вопросы по курсу
«ГОРНЫЕ МАШИНЫ И ОБОРУДОВАНИЕ»
(7-й семестр)
1. Классификация горных машин и требования к ним.
2. Структура горной машины и основные балансовые состояния.
3. Центр масс и центр давления.
4. Ядро сечения гусеничного хода, давления на опорное основание.
5. Способы разрушения горных пород. Силы, действующие на резец.
6. Удельные затраты энергии на разрушение резанием и способы их выра-
жения.
7. Факторы, влияющие на величину удельных затрат. Толщина стружки и ее
влияние.
8. Толщина стружки при работе цилиндрической фрезы.
9. Толщина стружки цепного бара.
10. Толщина стружки при работе винтовой фрезы.
11. Классификация механизмов перемещения. Кинематика гусеничного хода.
12. Теоретическая и действительная скорость движения. Буксование гусенич-
ного хода.
13. Мощность для передвижения гусеничного хода по прямой. Силы сопро-
тивления движению.
14. Коэффициент сопротивления мятию грунта и его составляющие.
15. Условия возможности движения по прямой.
16. Кинематика поворота гусеничного хода. Радиус и угловая скорость пово-
рота.
17. Уравнения равновесия гусеничной машины при повороте.
18. Центры вращения опорных ветвей в простейшем случае поворота.
19. Тяговые усилия гусеничных лент при повороте.
20. Мощность для поворота гусеничной машины. Условия возможности по-
ворота.
21. Колесный движитель. Режимы движения колеса.
22. Силы, действующие на ведущее и ведомое колеса.
23. Радиусы деформируемого колеса, буксование.
24. Мощность для передвижения колесной машины по прямой. Условия воз-
можности движения.
25. Сопротивление деформированию грунта колесом.
26. Схемы поворота колесных машин.
27. Определение размеров колеса по условиям допустимых давления и сопро-
тивления движению.
28. Мощность для поворота колесной машины.
29. Железнодорожный колесный ход. Мощность для его передвижения.
30. Проходческие комбайны, их классификация и схемы обработки забоя.
31. Энергетический баланс проходческого комбайна с соосными бурами.
32. Мощность для работы центрального бура.
33. Мощность для работы внешнего бура.

34. Мощность для работы бермовых фрез.
35. Мощность для работы отрезных коронок.
36. Мощность для передвижения комбайна.
37. Сила сопротивления подаче центрального бура.
38. Сила сопротивления подаче внешнего бура.
39. Сила сопротивления подаче бермовых фрез и отрезных коронок.
40. Бункер-перегружатель и мощность для его работы.
41. Самоходные вагоны. Мощность для работы в двух режимах.
42. Резец и силы, действующие на него. Удельное сопротивление резанию.
43. Силы, действующие на гусеницу при прямолинейном движении.
44. Силы, действующие на гусеницу при повороте.