ГОУ ЦО № 1432

Основоположники ЛОГИКИ

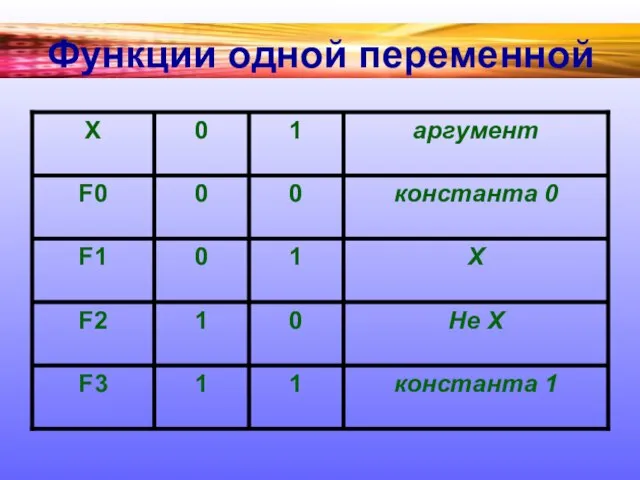
Функции одной переменной
Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.
Логический элемент — это устройство, реализующее ту или иную логическую функцию. Y=f(X1,X2,X3,...,Xn) — логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

Функции одной переменной

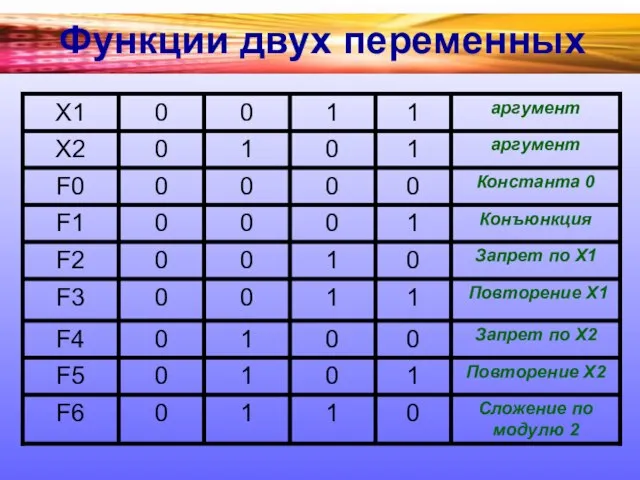
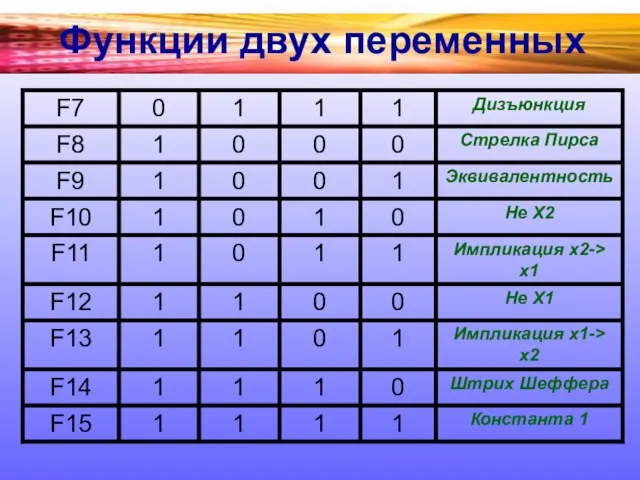
Функции двух переменных
Таблица истинности функции двух переменных Y=F(X1,Х2) содержит 4 строки, а число функций двух переменных равно 16.
Рассмотрим все эти функции двух переменных.

Функции двух переменных

Функции двух переменных

Карты Карно
Склейку клеток карты Карно можно осуществлять по единицам
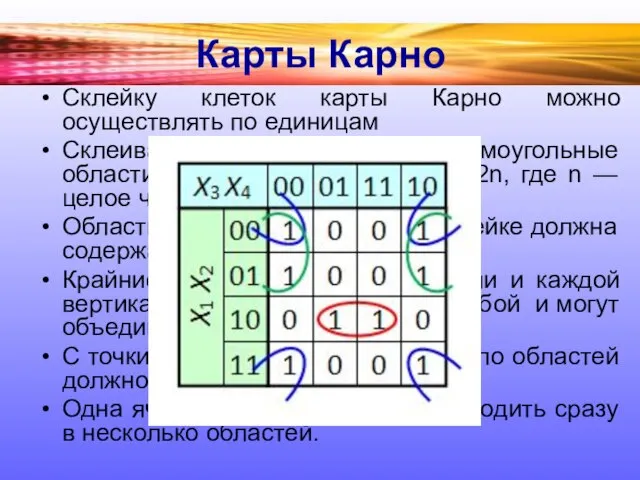
Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.
Область, которая подвергается склейке должна содержать только единицы (нули).
Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники.
С точки зрения минимальности число областей должно быть как можно меньше.
Одна ячейка карты Карно может входить сразу в несколько областей.

Представление функций
через И-ИЛИ-НЕ
Штрих Шеффера
¬X1 V ¬X2

Представление функций
через И-ИЛИ-НЕ
Стрелка Пирса
¬X1¬X2

Представление функций
через И-ИЛИ-НЕ
Эквивалентность
¬X1¬X2 V X1X2

Представление функций
через И-ИЛИ-НЕ
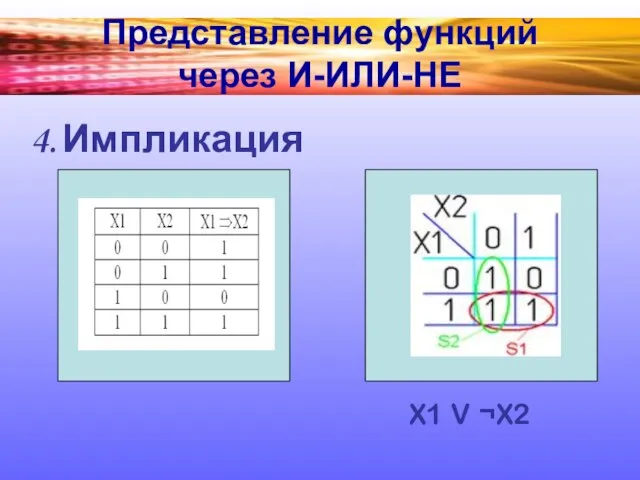
Импликация
X1 V ¬X2

Выводы
Теория логических функций прошла долгую историю от Аристотеля до наших дней. В современном виде её сформулировал Джорж Буль.
Логические функции являются математической основой современных вычислительных устройств. Для реализации логических функций в вычислительных устройствах важно унифицировать и минимизировать их представление.
Любая логическая функция может быть представлена как комбинация базовых логических функций И, ИЛИ, НЕ.
Для минимизации представления произвольных логических функций двух переменных удобно использовать карты Карно.
В работе приведены минимальные представления всех логических функций двух переменных через базовые функции И, ИЛИ, НЕ.

Авторы