ГРАДИЕНТНЫЙ ВЕТЕР ДЕЙСТВИТЕЛЬНЫЙ ВЕТЕР ИЗМЕНЕНИЕ ВЕТРА С ВЫСОТОЙ

ГРАДИЕНТНЫЙ ВЕТЕР
В случае криволинейных изобар возникает центробежная сила. Она всегда направлена в сторону выпуклости (от центра циклона или антициклона в сторону периферии).
Когда осуществляется равномерное горизонтальное движение воздуха без трения при криволинейных изобарах, то в горизонтальной плоскости уравновешиваются 3 силы: сила барического градиента G, сила вращения Земли K и центробежная сила C.
Такое равномерное установившееся горизонтальное движение воздуха при отсутствии трения по криволинейным траекториям называется градиентным ветром.
Вектор градиентного ветра направлен по касательной к изобаре под прямым углом вправо в северном полушарии (влево – в южном) относительно вектора силы барического градиента.
Поэтому в циклоне – вихрь против часовой стрелки, а в антициклоне – по часовой стрелке в северном полушарии.

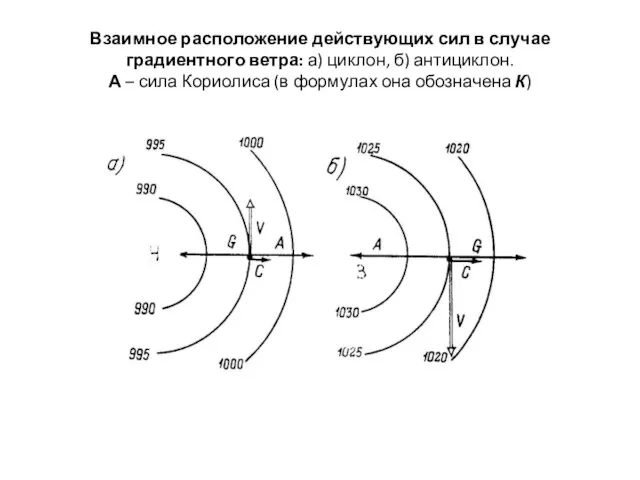
Взаимное расположение действующих сил в случае градиентного ветра: а) циклон, б) антициклон. А – сила Кориолиса (в формулах она обозначена К)

Рассмотрим влияние радиуса кривизны r на скорость градиентного ветра. При большом радиусе кривизны (r > 500 км) кривизна изобар (1/r) очень мала, близка к нулю. Радиус кривизны прямой прямолинейной изобары r → ∞ и ветер будет геострофическим. Геострофический ветер – частный случай градиентного ветра (при С = 0).
При небольшом радиусе кривизны (r < 500 км) в циклоне и антициклоне при круговых изобарах скорость градиентного ветра определяется следующими уравнениями:
В циклоне уравновешиваются силы G = K + C:
или
В антициклоне К = G + С:
Поэтому в циклоне: или

В антициклоне: или
То есть
В центре циклона и антициклона горизонтальный барический градиент
равен нулю, т.е.
Значит, G = 0 как источник движения. Следовательно, = 0.
Градиентный ветер является приближением к действительному ветру в свободной атмосфере циклона и антициклона.

Скорость градиентного ветра может быть получена при решении квадратного уравнения
- в циклоне:
в антициклоне:
В медленно перемещающихся барических образованиях (скорость перемещения не более 40 км/ч) в средних широтах при большой кривизне изогипс (1/r) → ∞ (малом радиусе кривизны r ≤ 500 км) на изобарической поверхности используют следующие соотношения между градиентным и геострофическим ветром:
При циклонической кривизне ≈ 0,7
При антициклонической кривизне ≈ 1,5

При большой кривизне изобар у поверхности Земли (1/r) → ∞ (радиус кривизны r ≤ 500 км):
при циклонической кривизне ≈ 0,7
при антициклонической кривизне ≈ 0,3
Геострофический ветер используется:
при прямолинейных изогипсах и изобарах и
при среднем радиусе кривизны 500 км < r < 1000км,
а также при большой кривизне изобар (r < 500 км) в быстро перемещающихся барических образованиях.

ЗАКОН ВЕТРА
Связь направления приземного ветра с направлением горизонтального барического градиента была сформулирована в 19 веке голландским ученым Бейс-Балло в виде правила (закона).
ЗАКОН ВЕТРА: Если смотреть по направлению ветра, то низкое давление будет слева и несколько впереди, а высокое – справа и несколько позади (в северном полушарии). При проведении изобар на синоптических картах учитывают направление ветра: направление изобары получают, повернув стрелку ветра вправо (по часовой стрелке) примерно на 30-45°.

ДЕЙСТВИТЕЛЬНЫЙ ВЕТЕР
Реальные движения воздуха не стационарны. Поэтому характеристики действительного ветра у земной поверхности отличаются от характеристик геострофического ветра.
Рассмотрим действительный ветер в виде двух слагаемых:
V = + V′
V′ – агеострофическое отклонение
u = + u′ или u′ = u -
v = + v′ или v′ = v –
Запишем уравнения движения без учета силы трения:

Используем соотношение между горизонтальным градиентом давления и геопотенциала
Подставим в уравнения движения:

Поделим обе части уравнений на и подставим в уравнение геострофического ветра. Получим:
Агеострофические отклонения:

ВЛИЯНИЕ СИЛЫ ТРЕНИЯ НА ВЕТЕР
Под влиянием трения скорость приземного ветра в среднем в два раза меньше скорости геострофического ветра, а направление его отклоняется от геострофического в сторону барического градиента. Таким образом, действительный ветер отклоняется у поверхности земли от геострофического влево в северном полушарии и вправо – в южном.
Взаимное расположение сил. Прямолинейные изобары

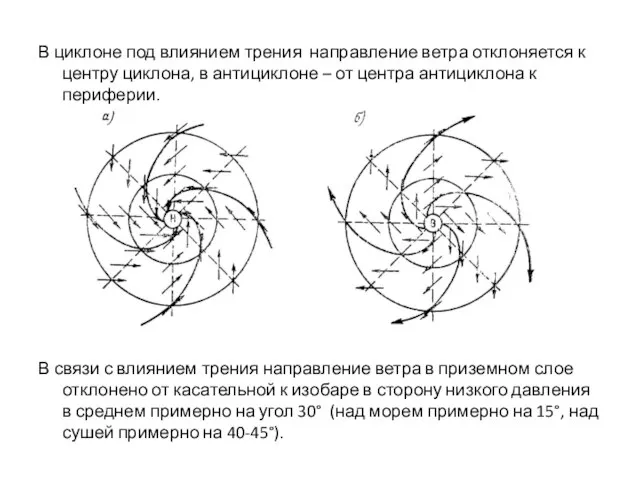
В циклоне под влиянием трения направление ветра отклоняется к центру циклона, в антициклоне – от центра антициклона к периферии.
В связи с влиянием трения направление ветра в приземном слое отклонено от касательной к изобаре в сторону низкого давления в среднем примерно на угол 30° (над морем примерно на 15°, над сушей примерно на 40-45°).

ИЗМЕНЕНИЕ ВЕТРА С ВЫСОТОЙ
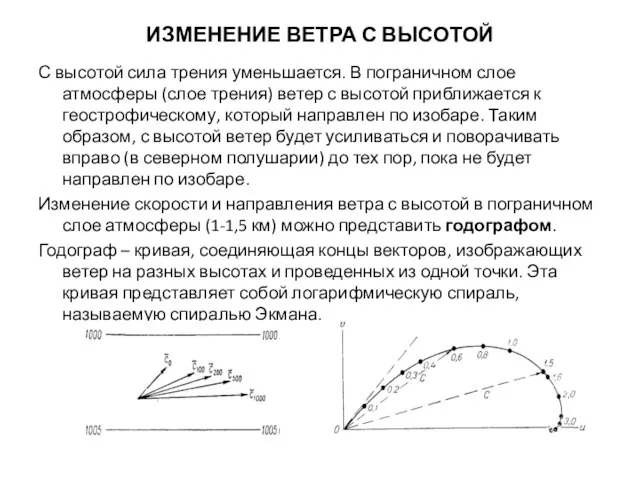
С высотой сила трения уменьшается. В пограничном слое атмосферы (слое трения) ветер с высотой приближается к геострофическому, который направлен по изобаре. Таким образом, с высотой ветер будет усиливаться и поворачивать вправо (в северном полушарии) до тех пор, пока не будет направлен по изобаре.
Изменение скорости и направления ветра с высотой в пограничном слое атмосферы (1-1,5 км) можно представить годографом.
Годограф – кривая, соединяющая концы векторов, изображающих ветер на разных высотах и проведенных из одной точки. Эта кривая представляет собой логарифмическую спираль, называемую спиралью Экмана.

ХАРАКТЕРИСТИКИ ПОЛЯ ВЕТРА
ЛИНИИ ТОКА
Линия тока – линия, в каждой точке которой вектор скорости ветра направлен по касательной в данный момент времени.
Таким образом, они дают представление о структуре поля ветра в данный момент времени (мгновенное поле скоростей).
В условиях градиентного или геострофического ветра линии тока будут совпадать с изобарами (изогипсами).
Вектор скорости действительного ветра в пограничном слое не параллелен изобарам (изогипсам). Поэтому линии тока действительного ветра пересекают изобары (изогипсы).
При проведении линий тока учитывают не только направление, но и скорость ветра: чем больше скорость, тем гуще располагаются линии тока.

Примеры линий тока у поверхности Земли
в приземном циклоне в приземном антициклоне
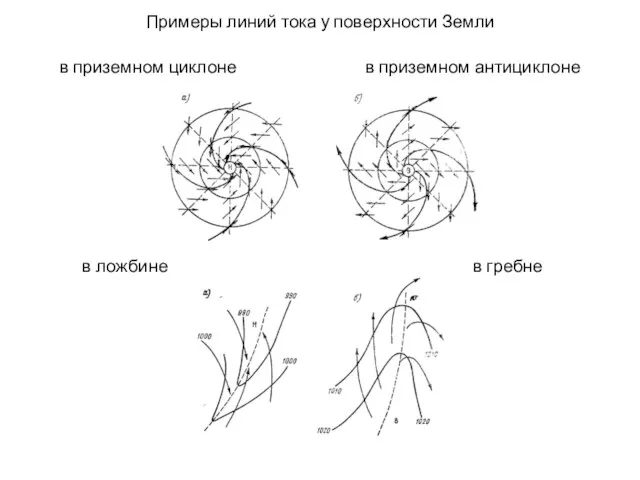
в ложбине в гребне

Линии тока в свободной атмосфере
в циклоне в антициклоне

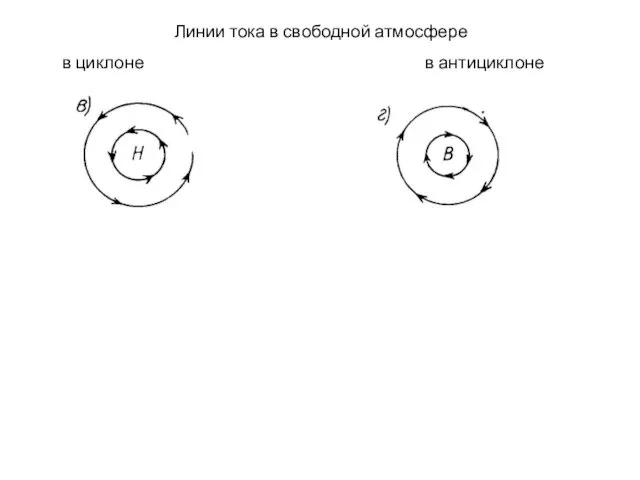
ТРАЕКТОРИИ ЧАСТИЦ ВОЗДУХА
Траектории частиц – пути индивидуальных воздушных частиц.
Т.е. траектория характеризует перемещение одной и той же частицы воздуха в последовательные моменты времени.
Траектории частиц можно приближенно рассчитать по последовательным синоптическим картам.
Метод траекторий в синоптической метеорологии позволяет решать две задачи:
определить, откуда переместится частица воздуха в данную точку за определенный промежуток времени;
определить, куда переместится частица воздуха из данной точки за определенный промежуток времени.
Траектории можно строить по картам АТ (чаще по АТ-700) и по приземным картам.
Используется графический способ расчета траектории с помощью градиентной линейки.

Пример построения траектории частицы воздуха (откуда переместится частица) по одной карте: А – пункт прогноза; В – середина пути частицы;
С – начальная точка траектории
С помощью нижней части градиентной линейки по расстоянию между изогипсами определяют скорость геострофического ветра (V, км/ч).
Линейку прикладывают нижней шкалой (V, км/ч) по нормали к изогипсам примерно в середине пути. По шкале (V, км/ч) между двумя изогипсами (в точке пересечения со второй изогипсой) определяют среднюю скорость Vcp.