Содержание
- 2. Графический способ решения уравнений состоит в построении на одной координатной плоскости графиков двух функций и нахождении
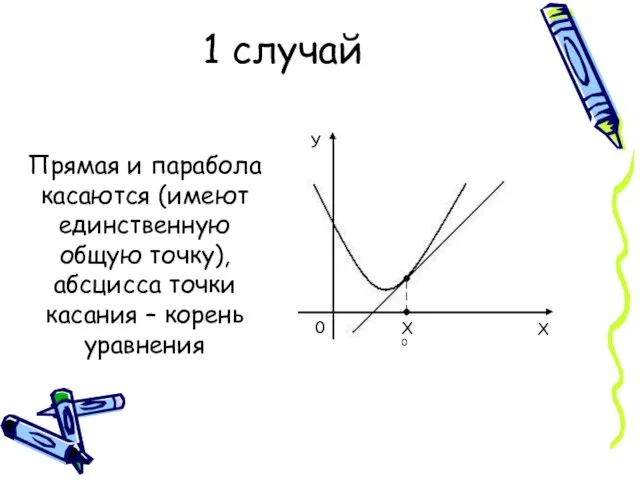
- 3. 1 случай Прямая и парабола касаются (имеют единственную общую точку), абсцисса точки касания – корень уравнения
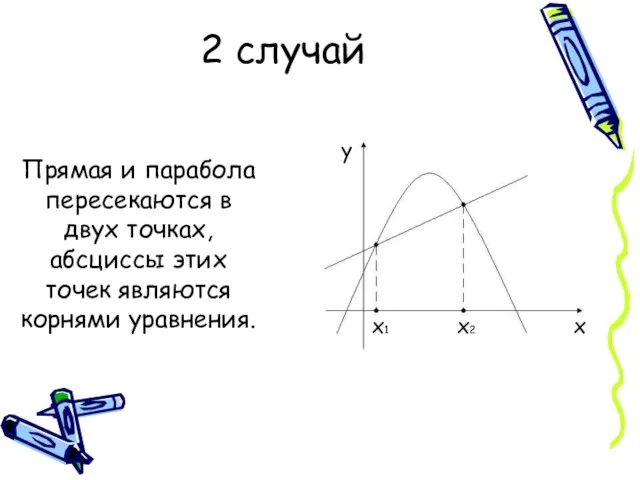
- 4. 2 случай Прямая и парабола пересекаются в двух точках, абсциссы этих точек являются корнями уравнения.
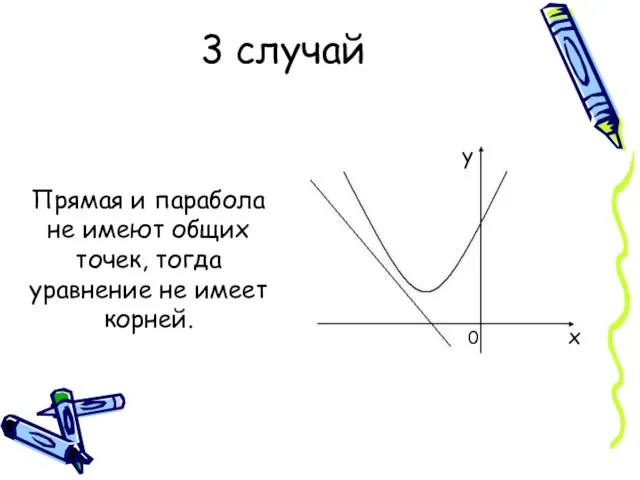
- 5. 3 случай Прямая и парабола не имеют общих точек, тогда уравнение не имеет корней.
- 6. Пример Решите графически уравнение х²+1,5х-2,5=0. Решение. Перепишем уравнение в виде х²=-1,5х+2,5. Рассмотрим функции у = х²
- 7. Задание на дом Решите графически уравнение: а) х²=0 б) 2х²+7=0 в) х²-2х=0
- 9. Скачать презентацию



 Учитель информатики в моем представлении
Учитель информатики в моем представлении Топливный элемент: проблемы и перспективы
Топливный элемент: проблемы и перспективы Овощи. Приготовление блюд из овощей
Овощи. Приготовление блюд из овощей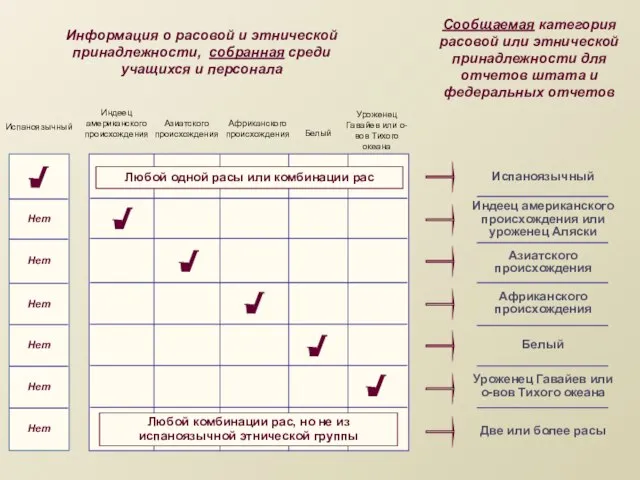 Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала
Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала Возможности интернета в развитии интеллектуального потенциала старшеклассников
Возможности интернета в развитии интеллектуального потенциала старшеклассников Тоталитарное государство
Тоталитарное государство Морской лев
Морской лев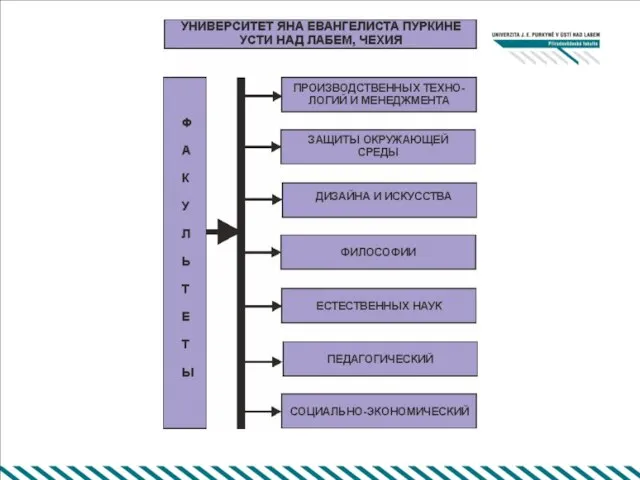 Университет Я. Э. Пуркине Факультет естественных наук Основан 4 ноября 2005 года. Цель факультета - подготовка бакалавров, магистров и
Университет Я. Э. Пуркине Факультет естественных наук Основан 4 ноября 2005 года. Цель факультета - подготовка бакалавров, магистров и Принципы и функции налогообложения
Принципы и функции налогообложения Технологическая карта
Технологическая карта Пульт горочный ПГУ-65
Пульт горочный ПГУ-65 ОАО «Российский банк развития»
ОАО «Российский банк развития» Сравнение скриптов TEMS
Сравнение скриптов TEMS Энергетика: вчера, сегодня, завтра
Энергетика: вчера, сегодня, завтра Житие Бориса и Глеба
Житие Бориса и Глеба Техника классического лыжного хода
Техника классического лыжного хода Салават Юлаев - национальный герой башкирского народа
Салават Юлаев - национальный герой башкирского народа ГРЕЙДИНГ
ГРЕЙДИНГ Основы православной культуры
Основы православной культуры Моя семья. Фотоальбом Артёма Тарасевича
Моя семья. Фотоальбом Артёма Тарасевича Методика Построение заборчика. Диагностика наглядно-действенного мышления у дошкольников
Методика Построение заборчика. Диагностика наглядно-действенного мышления у дошкольников Химические средства гигиены и косметики
Химические средства гигиены и косметики Колоноскопия и ирригоскопия. Виртуальная колоноскопия
Колоноскопия и ирригоскопия. Виртуальная колоноскопия Как пройти путь от создания идеи до действующего стартапа
Как пройти путь от создания идеи до действующего стартапа Презентація проекту“Порівняльний аналіз подій, що відбулися 150 років тому:1) 19 лютого(3 березня) 1861 р. цар Олександр ІІ видав маніф
Презентація проекту“Порівняльний аналіз подій, що відбулися 150 років тому:1) 19 лютого(3 березня) 1861 р. цар Олександр ІІ видав маніф Пантелеймон Куліш
Пантелеймон Куліш МЕЖДУНАРОДНЫЙ НАЛОГОВЫЙ КОНГРЕСС Заемное финансирование – практические аспекты Контролируемая задолженность: понятие и сложн
МЕЖДУНАРОДНЫЙ НАЛОГОВЫЙ КОНГРЕСС Заемное финансирование – практические аспекты Контролируемая задолженность: понятие и сложн Планирование и управление временем
Планирование и управление временем