Содержание
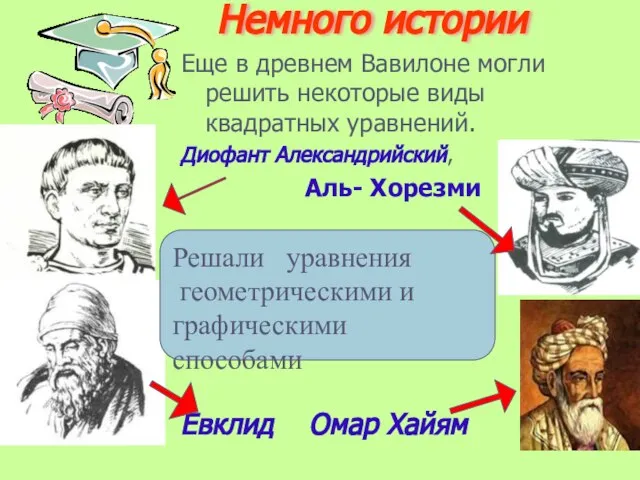
- 2. Немного истории Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми
- 3. Для графического решения квадратного уравнения представьте его в одном из видов: ax2 + bx +c =
- 4. Алгоритм графического решения квадратных уравнений Ввести функцию f(x), равную левой части и g(x) , равную правой
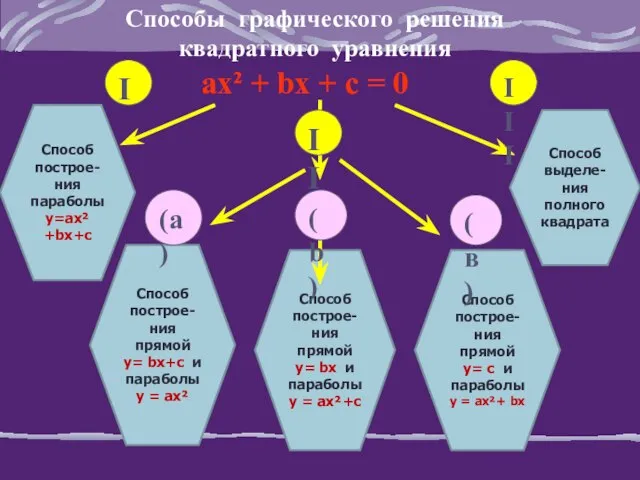
- 5. Способы графического решения квадратного уравнения ах² + bх + с = 0 Способ поcтрое- ния параболы
- 6. «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре
- 7. Графическое решение квадратного уравнения Иллюстрация на одном примере
- 8. Алгоритм решения квадратного уравнения графическим способом Способ 1 Построить график функции y=ax2+bx+c Найти точки пересечения графика
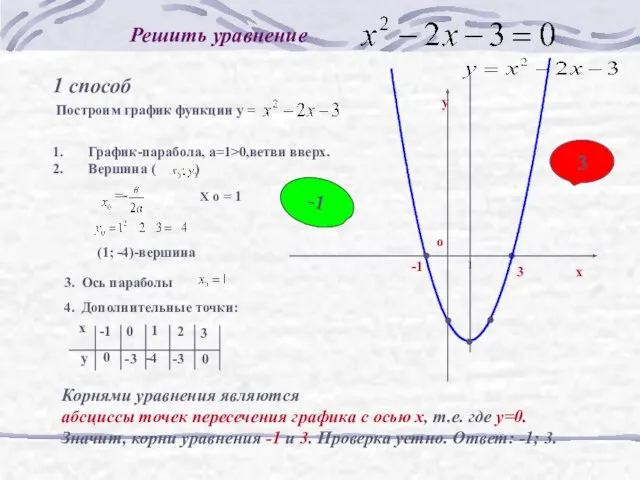
- 9. Решить уравнение 1 способ Корнями уравнения являются абсциссы точек пересечения графика с осью х, т.е. где
- 10. Алгоритм построения параболы найти координаты вершины; провести ось параболы; отметить на оси абсцисс две точки, симметричные
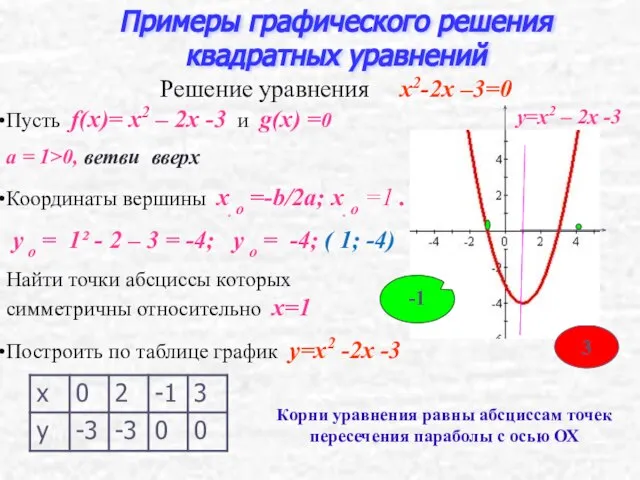
- 11. Пусть f(x)= x2 – 2x -3 и g(x) =0 а = 1>0, ветви вверх Координаты вершины
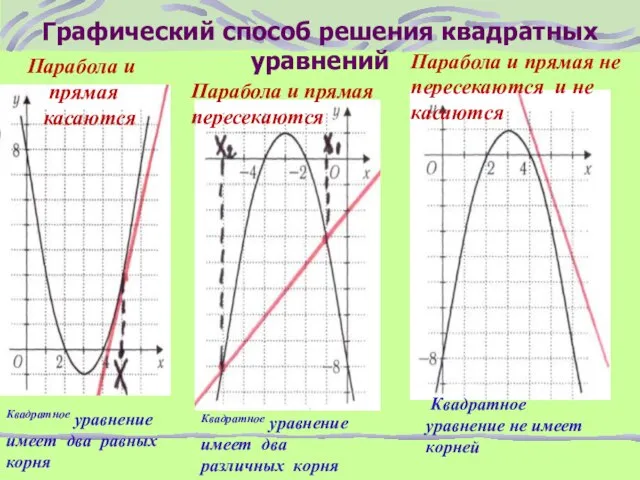
- 12. Графический способ решения квадратных уравнений Парабола и прямая касаются Парабола и прямая пересекаются Квадратное уравнение имеет
- 13. Алгоритм решения квадратного уравнения графическим способом Способ 2(а) Построить графики функции y=ax2 и у = bx+
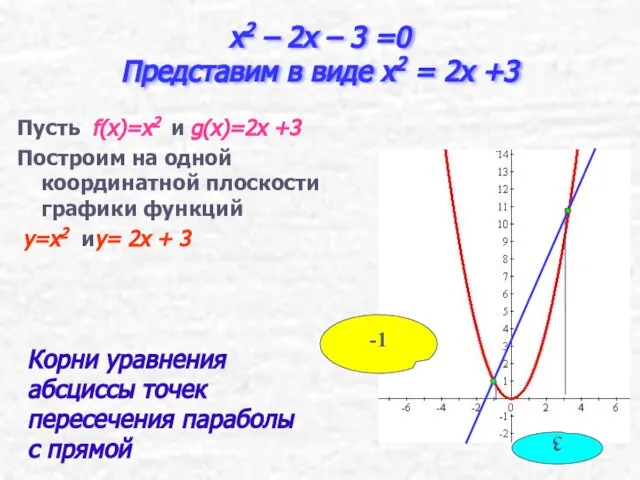
- 14. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и
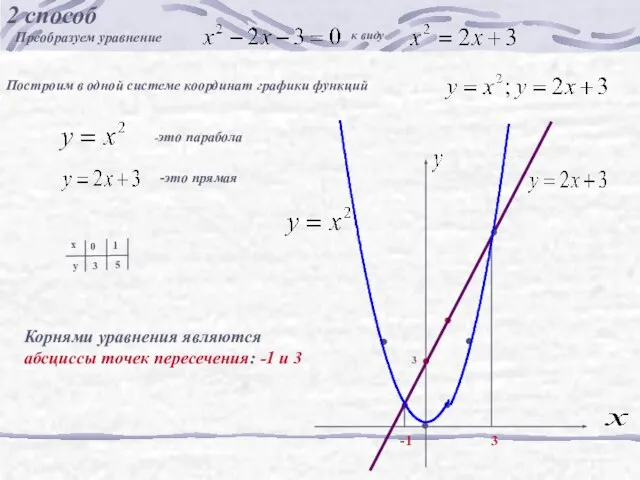
- 15. 2 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций -это парабола -это
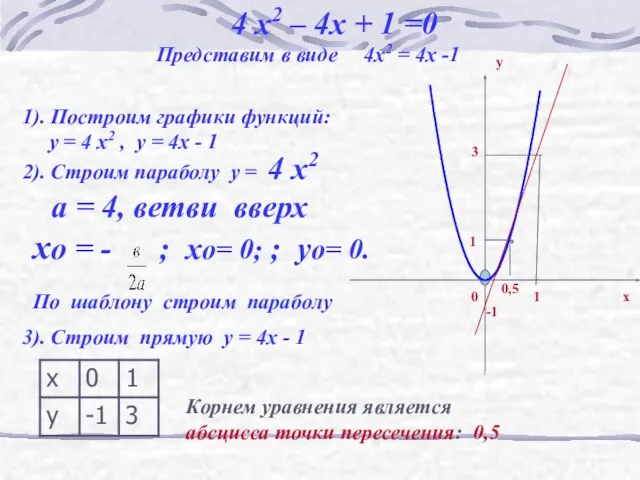
- 16. 4 x2 – 4x + 1 =0 Представим в виде 4x2 = 4x -1 1). Построим
- 17. Алгоритм решения квадратного уравнения графическим способом Способ 2 (b) Преобразовать уравнение к виду ax2+с = bx
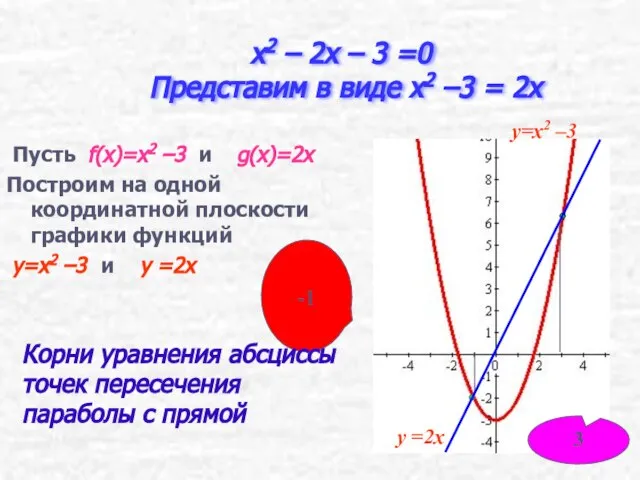
- 18. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3
- 19. x2 – 4x + 5 =0 Представим в виде x2 +5 = 4x Пусть f(x)=x2 +5
- 20. Алгоритм решения квадратного уравнения графическим способом Способ 2(в) Построить графики функции y=ax2 + bx и у
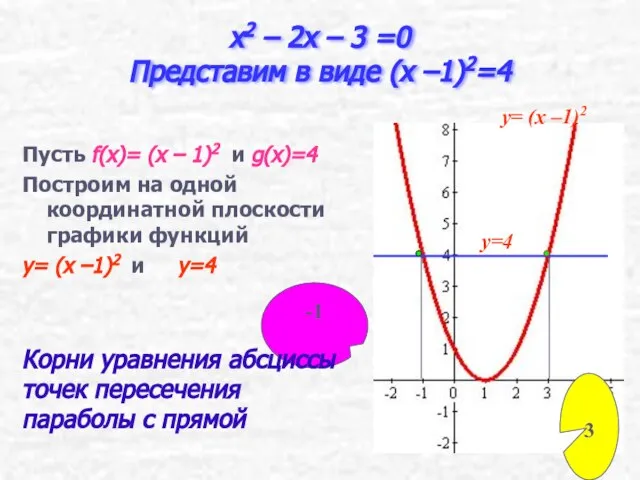
- 21. x2 – 2x – 3 =0 Представим в виде x2 – 2x = 3 Пусть f(x)=
- 22. Алгоритм решения квадратного уравнения графическим способом Способ 3 (выделение полного квадрата) Преобразовать уравнение к виду a(x+l)2
- 23. Выделение квадрата двучлена. x2 – 2x + 1 = 3 + 1 ( x –1)2=4. x2
- 24. x2 – 2x – 3 =0 Представим в виде (x –1)2=4 Пусть f(x)= (x – 1)2
- 25. Решите графически уравнение Группа А Бычев Андрей Ерофеева Ксения Каминская Света Лобов Егор Лукьяненко Вероника Осипов
- 26. Сколько нам открытий чудных готовит просвещения дух?
- 27. Решить графически уравнение
- 28. Как решить уравнение? Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут
- 29. Решить графически уравнение
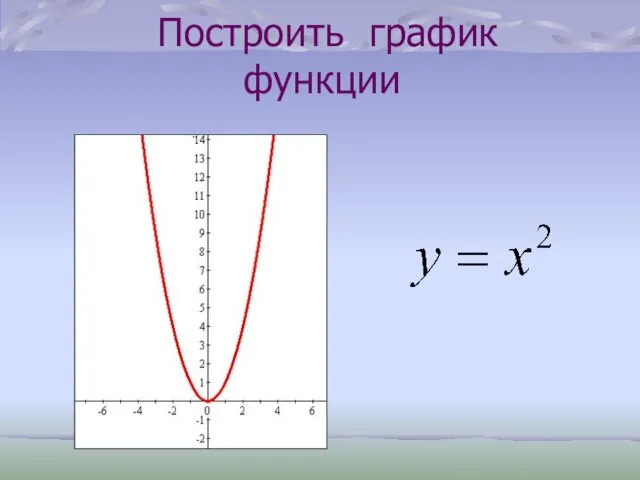
- 30. Построить график функции
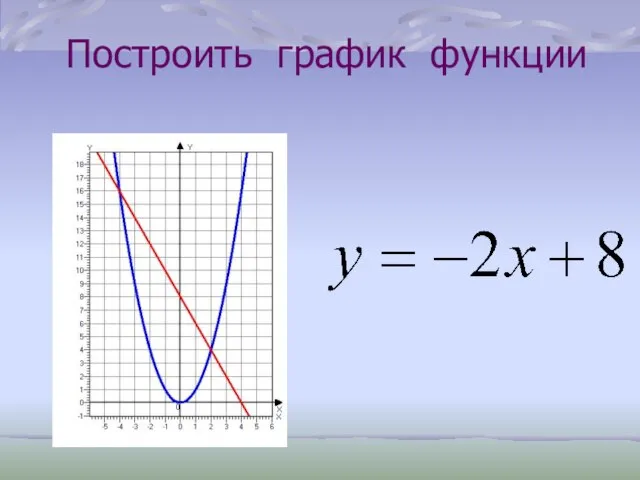
- 31. Построить график функции
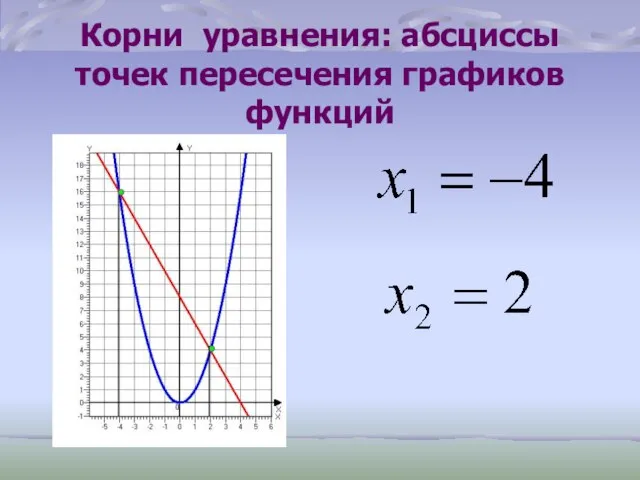
- 32. Корни уравнения: абсциссы точек пересечения графиков функций
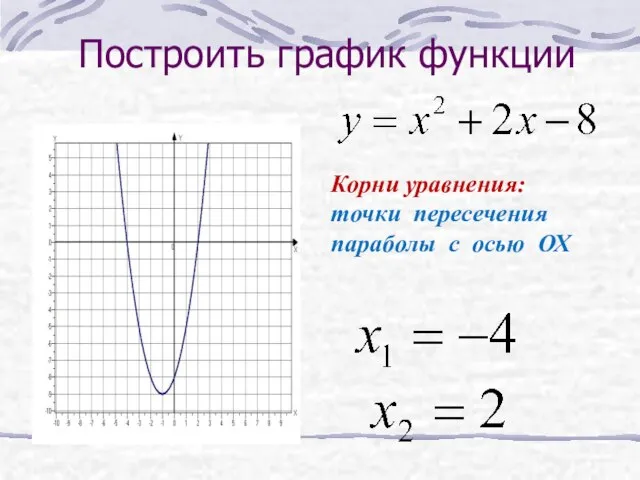
- 33. Построить график функции Корни уравнения: точки пересечения параболы с осью ОХ
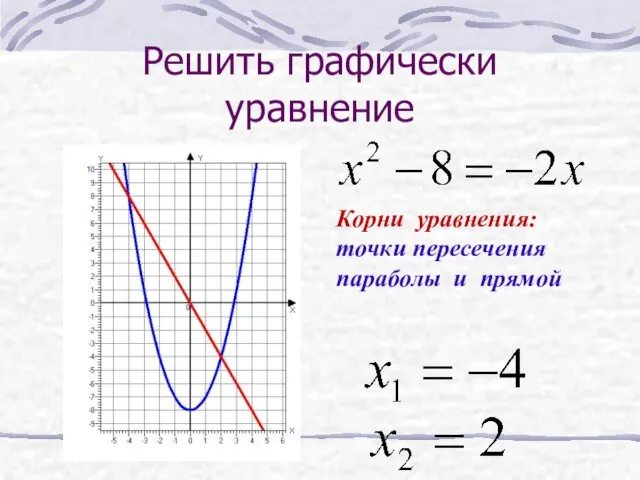
- 34. Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
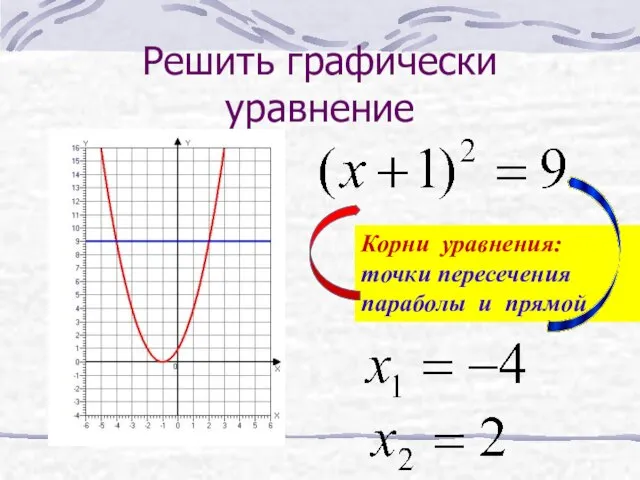
- 35. Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
- 36. Итог Познакомились: с графическим методом решения квадратных уравнений; с различными способами графического решения квадратных уравнений. закрепили
- 37. Заключительное слово учителя: «Чем больше и глубже вам удастся усвоить азы математики и научиться пользоваться ее
- 39. Скачать презентацию




















 MU6100_TrainingManual_170201
MU6100_TrainingManual_170201 вікі
вікі Архитектура западноевропейского средневековья
Архитектура западноевропейского средневековья «Надежда Дурова участница Отечественной войны 1812 года»
«Надежда Дурова участница Отечественной войны 1812 года» Бумажные превращения
Бумажные превращения Природа Архангельской области
Природа Архангельской области Аменорея алгоритмы диагностики и лечения
Аменорея алгоритмы диагностики и лечения  Сетевая акция Фруктово-ягодный книжный коктейль
Сетевая акция Фруктово-ягодный книжный коктейль Проведение контрольной работы
Проведение контрольной работы Презентация программ пришкольного оздоровительного лагеря
Презентация программ пришкольного оздоровительного лагеря слайд-шоу фокусника-иллюзиониста Леонида Зангиева 2
слайд-шоу фокусника-иллюзиониста Леонида Зангиева 2 Информатика в датах
Информатика в датах Допинг в спорте: всегда ли все средства хороши
Допинг в спорте: всегда ли все средства хороши Презентация на тему Ориентирование
Презентация на тему Ориентирование  Борис Корнилов. Слово о поэте
Борис Корнилов. Слово о поэте Мотивация учения, поведения и выбора профессии.
Мотивация учения, поведения и выбора профессии. Применение жиров
Применение жиров Психолого-педагогическое сопровождение профессионального самоопределения старшеклассников в рамках сетевого взаимодействия о
Психолого-педагогическое сопровождение профессионального самоопределения старшеклассников в рамках сетевого взаимодействия о Экологические проблемы утилизации бытовых отходов в мегаполюсе …
Экологические проблемы утилизации бытовых отходов в мегаполюсе … Свобода и необходимость человеческой деятельности
Свобода и необходимость человеческой деятельности Объект и предмет военного права. (лекция 3.1)
Объект и предмет военного права. (лекция 3.1) Демократизасийа вя авторитарлыг
Демократизасийа вя авторитарлыг Презентация на тему НАПРЯЖЕННОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.ЛИНИИ НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Презентация на тему НАПРЯЖЕННОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.ЛИНИИ НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ красота человека. женский образ
красота человека. женский образ Новые возможности для участников ООО в связи с изменениями в законодательстве
Новые возможности для участников ООО в связи с изменениями в законодательстве Математика - это не скучно!
Математика - это не скучно! Деятельностный подход
Деятельностный подход  Презентация на тему Драма Гроза
Презентация на тему Драма Гроза