Содержание
- 2. Задача линейного программирования с двумя неизвестными может быть решена графически Замечание: К такой форме может быть
- 3. Пусть задача линейного программирования задана в виде:
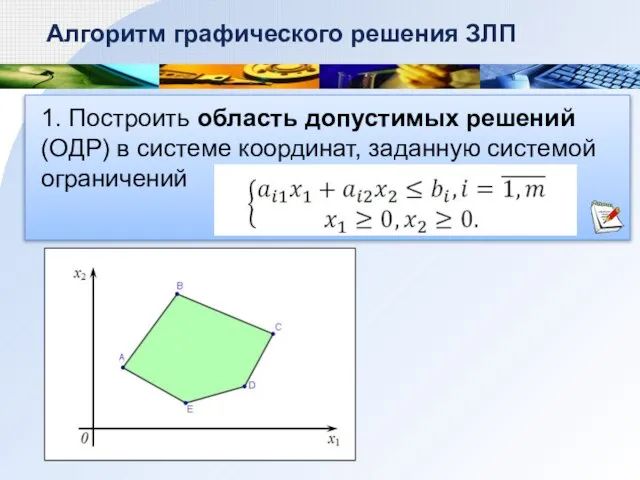
- 4. 1. Построить область допустимых решений (ОДР) в системе координат, заданную системой ограничений Алгоритм графического решения ЗЛП
- 5. 2. Построить градиент целевой функции F = с1х1+с2х2 (вектор нормали к прямой с1х1+с2х2 = F) Алгоритм
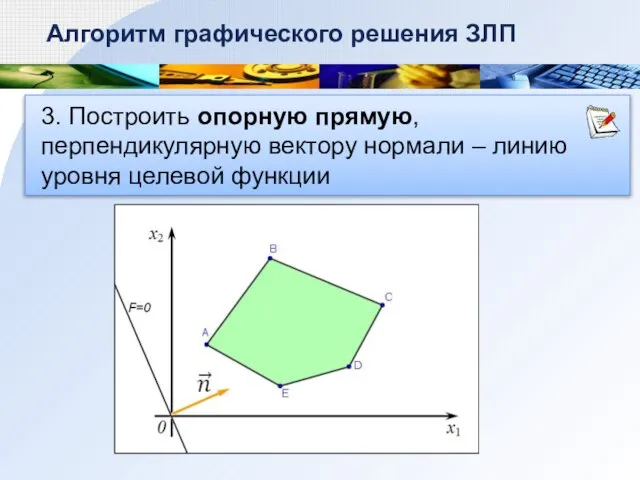
- 6. 3. Построить опорную прямую, перпендикулярную вектору нормали – линию уровня целевой функции Алгоритм графического решения ЗЛП
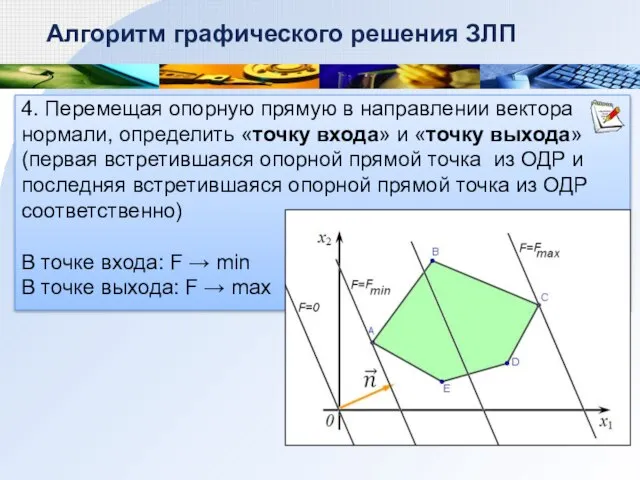
- 7. 4. Перемещая опорную прямую в направлении вектора нормали, определить «точку входа» и «точку выхода» (первая встретившаяся
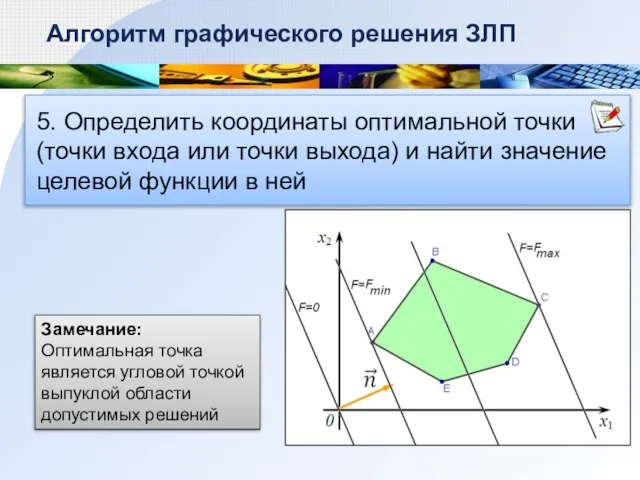
- 8. 5. Определить координаты оптимальной точки (точки входа или точки выхода) и найти значение целевой функции в
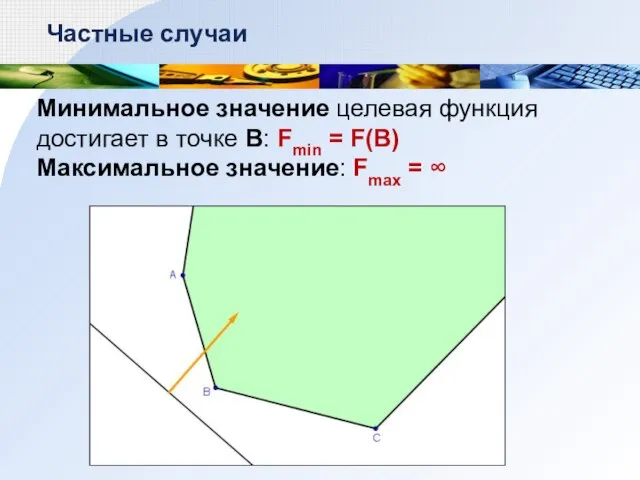
- 9. Минимальное значение целевая функция достигает в точке В: Fmin = F(B) Максимальное значение: Fmax = ∞
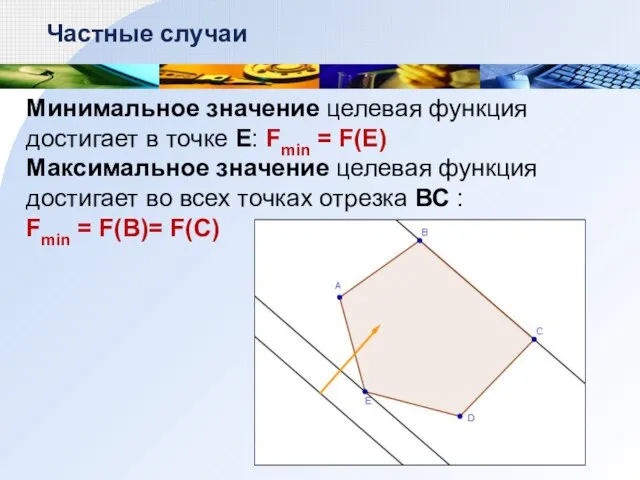
- 10. Минимальное значение целевая функция достигает в точке E: Fmin = F(E) Максимальное значение целевая функция достигает
- 11. Решить графически ЗЛП
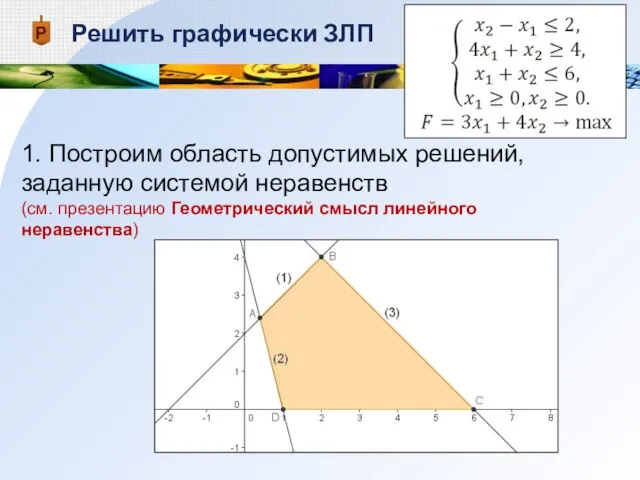
- 12. Решить графически ЗЛП 1. Построим область допустимых решений, заданную системой неравенств (см. презентацию Геометрический смысл линейного
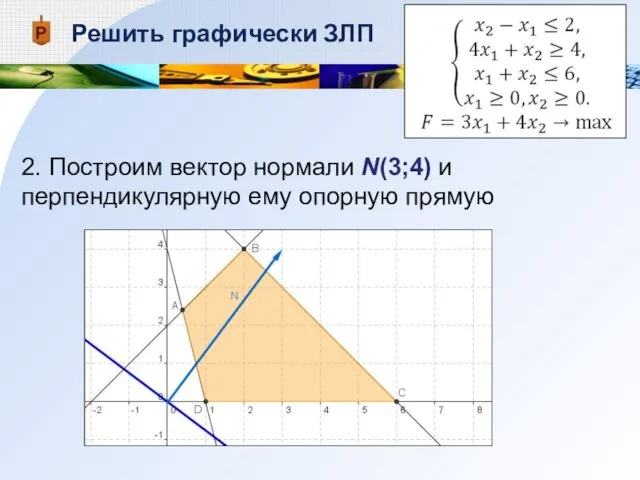
- 13. Решить графически ЗЛП 2. Построим вектор нормали N(3;4) и перпендикулярную ему опорную прямую
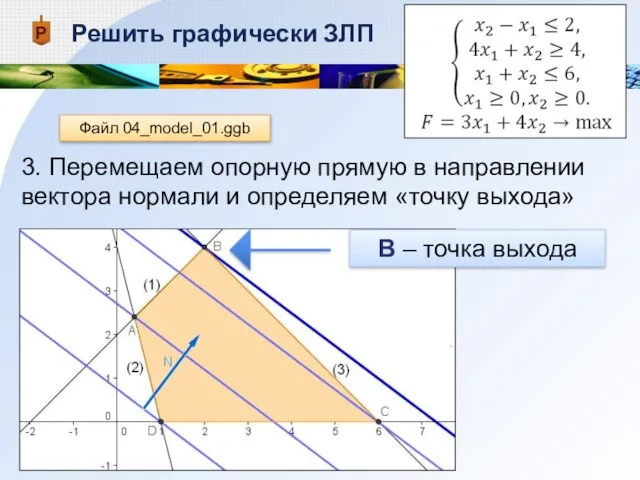
- 14. Решить графически ЗЛП 3. Перемещаем опорную прямую в направлении вектора нормали и определяем «точку выхода» Файл
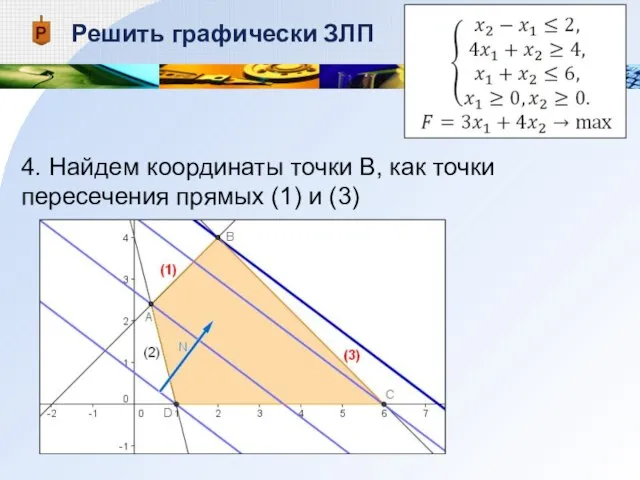
- 15. Решить графически ЗЛП 4. Найдем координаты точки В, как точки пересечения прямых (1) и (3)
- 16. Решить графически ЗЛП 4. Найдем координаты точки В, как точки пересечения прямых (1) и (3):
- 17. Решить графически ЗЛП 5. Найдем значение целевой функции в точке В
- 18. Решить графически ЗЛП Ответ:
- 20. Скачать презентацию







 Тема урока: Треугольники. Центр тяжести. Тип урока: Интегрированный урок физики и математики с применением информационных техн
Тема урока: Треугольники. Центр тяжести. Тип урока: Интегрированный урок физики и математики с применением информационных техн Кактус из бумаги
Кактус из бумаги Закрепление пройденного. Права человека
Закрепление пройденного. Права человека Анализ деятельности кредитной организации
Анализ деятельности кредитной организации  Технология изготовления и организация производства сварной конструкции Опора для вентиляционных конструкций
Технология изготовления и организация производства сварной конструкции Опора для вентиляционных конструкций Презентация на тему Безопасность Огонь Вода Газ
Презентация на тему Безопасность Огонь Вода Газ В землянке
В землянке Слоаврь
Слоаврь Муниципальное дошкольное образовательное учреждение«Детский сад компенсирующего вида № 7»
Муниципальное дошкольное образовательное учреждение«Детский сад компенсирующего вида № 7» Процессы памяти и их нарушения при нервно-психических заболеваниях
Процессы памяти и их нарушения при нервно-психических заболеваниях Education jobs
Education jobs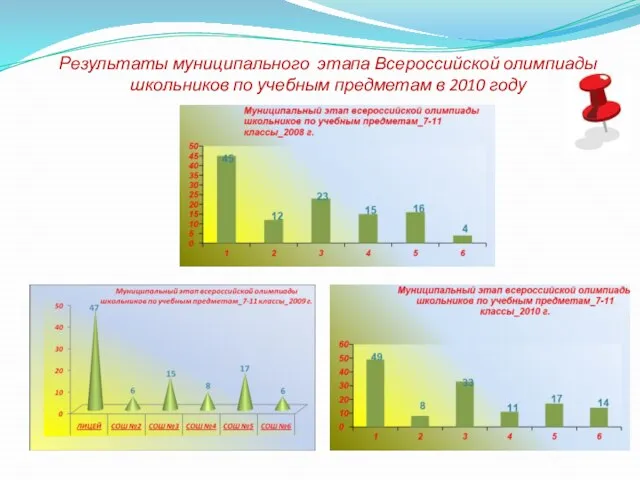 Результаты муниципального этапа Всероссийской олимпиады школьников по учебным предметам в 2010 году
Результаты муниципального этапа Всероссийской олимпиады школьников по учебным предметам в 2010 году BUSINESS JET TRAVEL
BUSINESS JET TRAVEL Алгебра.8 класс Решение квадратных уравнений по формуле.
Алгебра.8 класс Решение квадратных уравнений по формуле. Опыт организации работы команды разработчиков на основе Rational ClearQuest. Тонкая настройка.
Опыт организации работы команды разработчиков на основе Rational ClearQuest. Тонкая настройка. Презентация на тему Голосеменные Классификация
Презентация на тему Голосеменные Классификация Энергетическая стратегия России до 2030 года: переход к инновационной энергетике будущего
Энергетическая стратегия России до 2030 года: переход к инновационной энергетике будущего Технологии решения проблем ЭМС на электросетевых объектах
Технологии решения проблем ЭМС на электросетевых объектах Место и время счастья
Место и время счастья Презентация на тему АНАТОМИЯ ОРГАНА ЗРЕНИЯ
Презентация на тему АНАТОМИЯ ОРГАНА ЗРЕНИЯ  Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных
Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных Виртуальное путешествие Как встречают Новый год люди всех земных широт
Виртуальное путешествие Как встречают Новый год люди всех земных широт Презентация на тему Пищеварительная система
Презентация на тему Пищеварительная система  рекомендации по подготовке мультимедийной ПРЕЗЕНТАЦИИ
рекомендации по подготовке мультимедийной ПРЕЗЕНТАЦИИ Самолет президента спешит на помощь
Самолет президента спешит на помощь Греко-римская борьба. Тестирование физической подготовленности в ИВС
Греко-римская борьба. Тестирование физической подготовленности в ИВС Презентация на тему Шаблоны написания сочинений ОГЭ
Презентация на тему Шаблоны написания сочинений ОГЭ  Анализ инвестиционных процессов
Анализ инвестиционных процессов