Содержание
- 2. Определение модуля. Модулем числа называется расстояние от нуля до заданной точки на числовой прямой. | 6
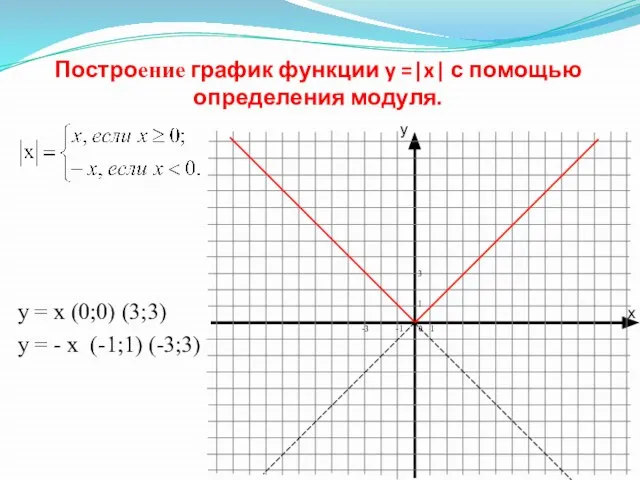
- 3. Построение график функции y =|x| с помощью определения модуля. y = x (0;0) (3;3) y =
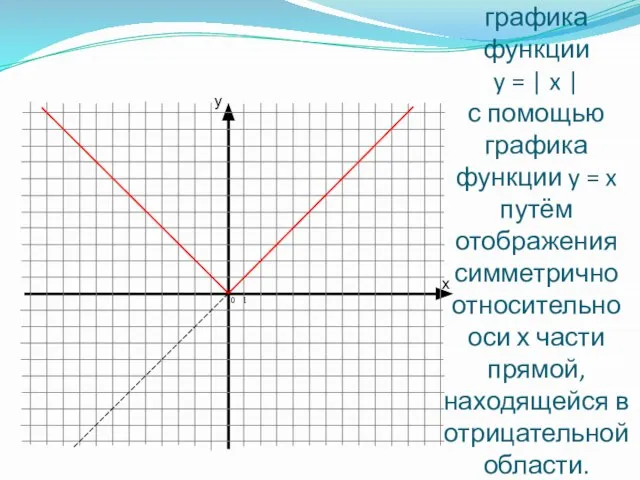
- 4. Построение графика функции y = | x | с помощью графика функции y = x путём
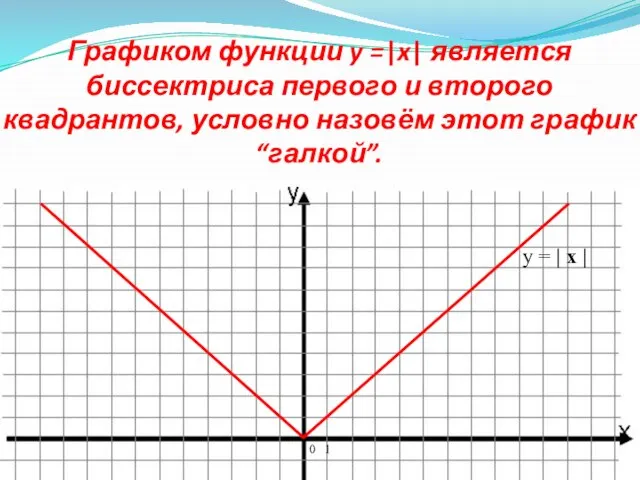
- 5. Графиком функции y =|x| является биссектриса первого и второго квадрантов, условно назовём этот график “галкой”. 0
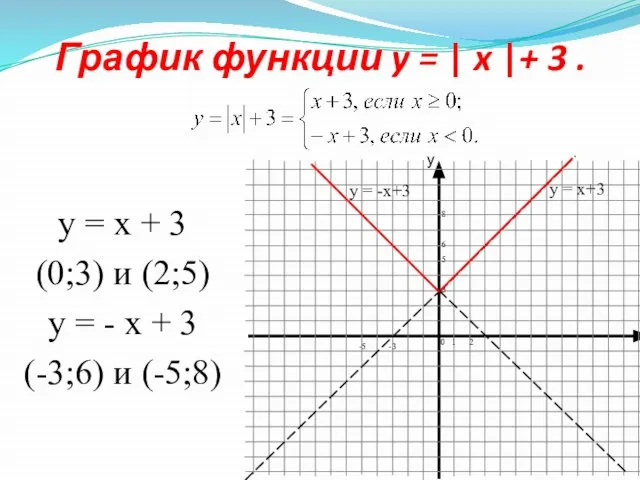
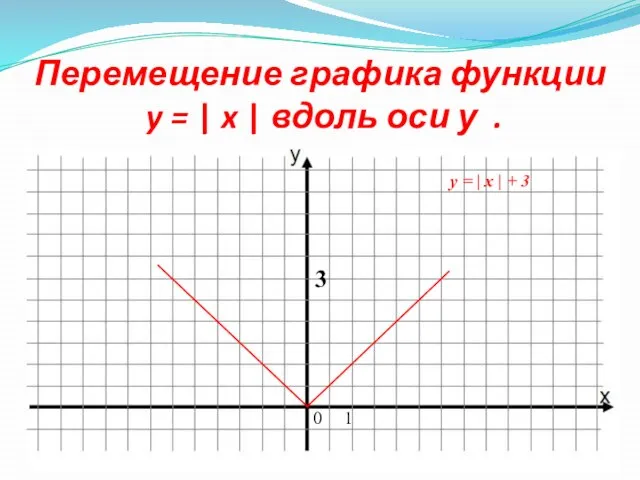
- 6. График функции y = | x |+ 3 . y = x + 3 (0;3) и
- 7. Перемещение графика функции y = | x | вдоль оси у . 0 1 3 y
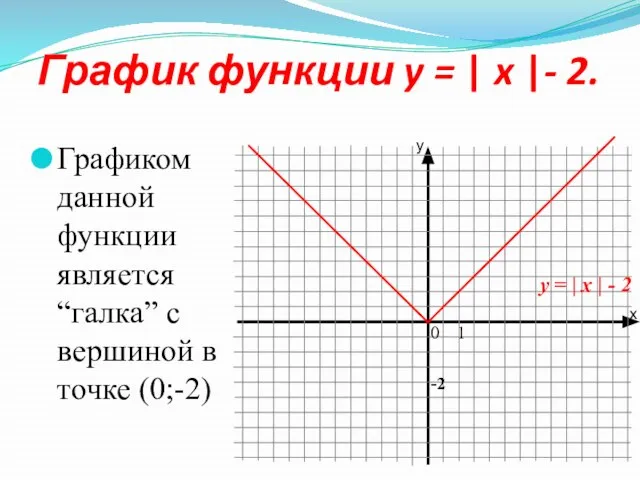
- 8. График функции y = | x |- 2. 0 1 Графиком данной функции является “галка” с
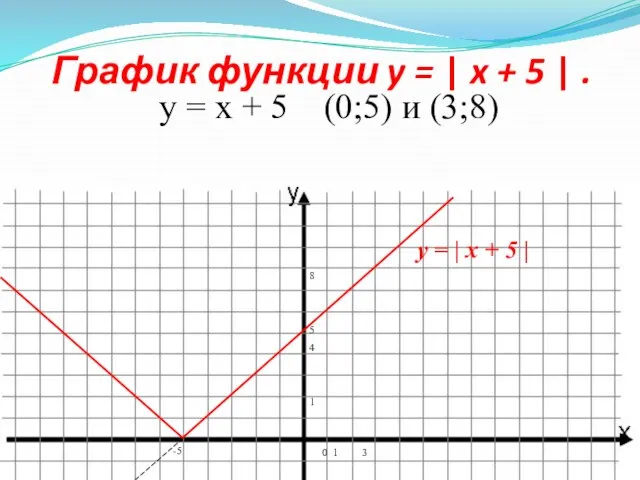
- 9. График функции y = | x + 5 | . y = x + 5 (0;5)
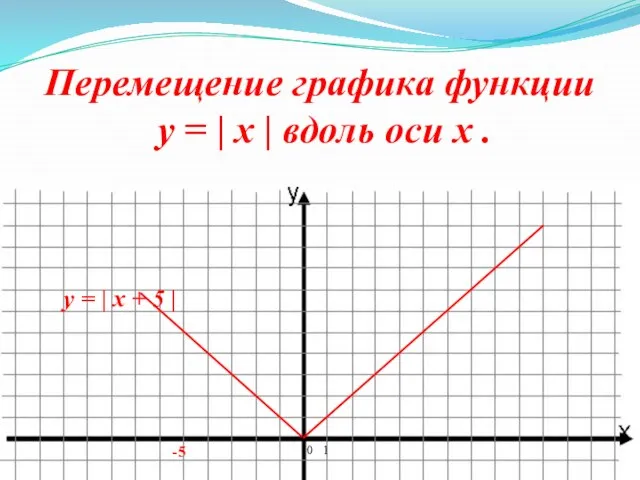
- 10. 0 1 -5 Перемещение графика функции y = | x | вдоль оси x . y
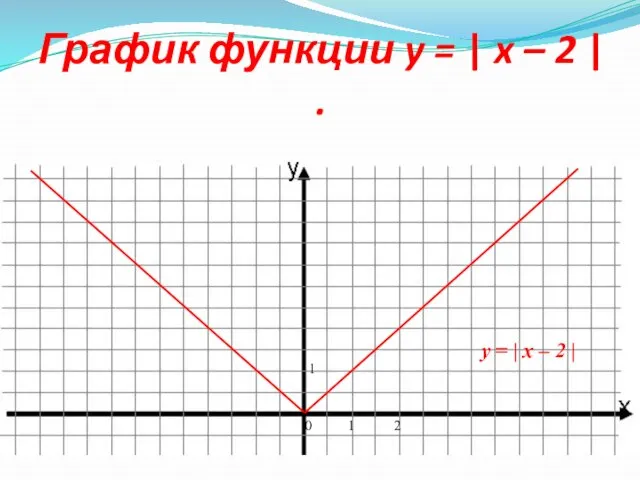
- 11. График функции y = | x – 2 | . 0 1 2 1 y =
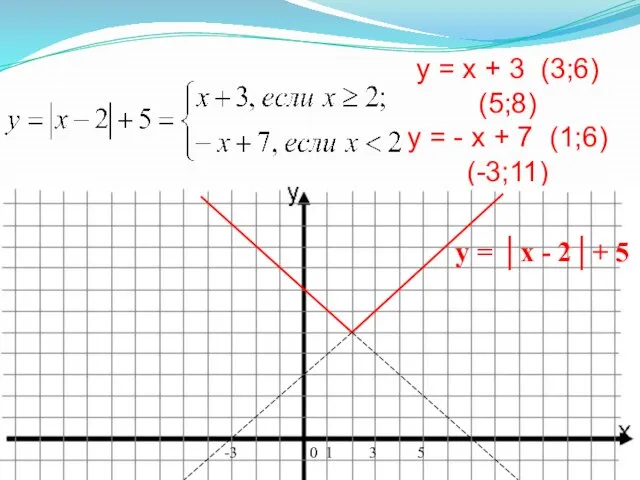
- 12. у = x + 3 (3;6) (5;8) у = - x + 7 (1;6) (-3;11) 0
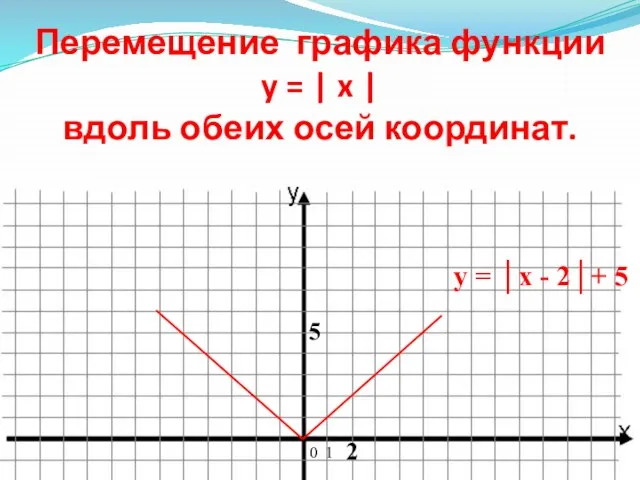
- 13. Перемещение графика функции y = | x | вдоль обеих осей координат. 0 1 5 2
- 14. Итак, в общем виде получили, что графиком функции: 1) y = |x| + m является “галка”
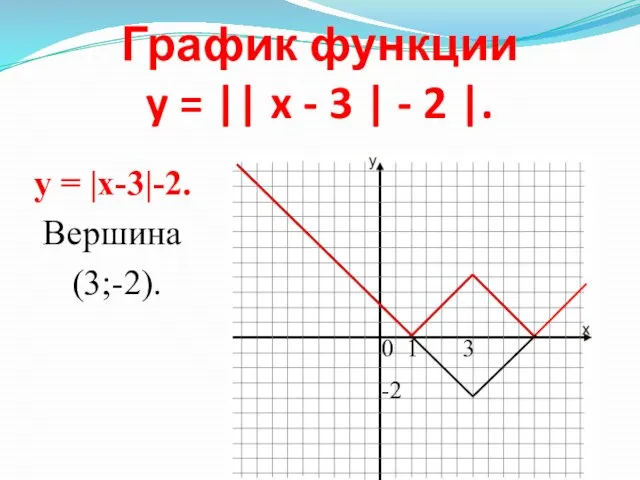
- 15. График функции y = || x - 3 | - 2 |. 0 1 3 -2
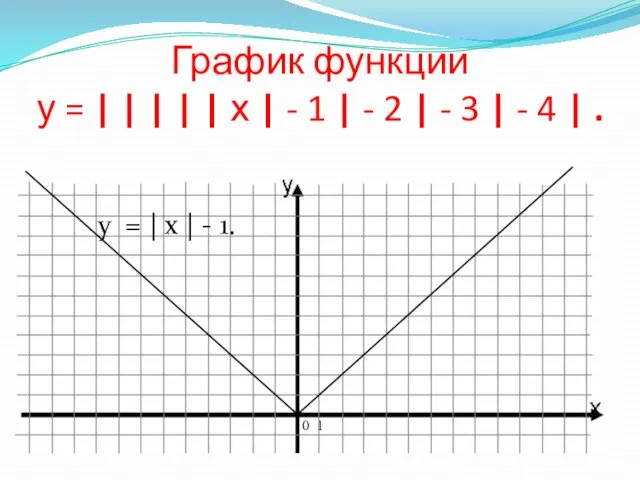
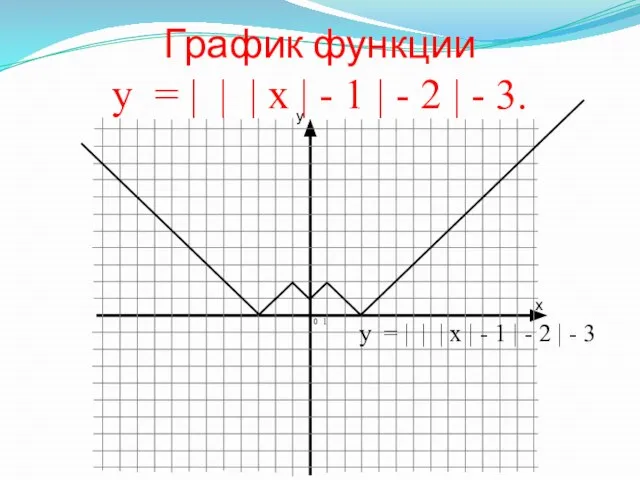
- 16. График функции у = | | | | | х | - 1 | - 2
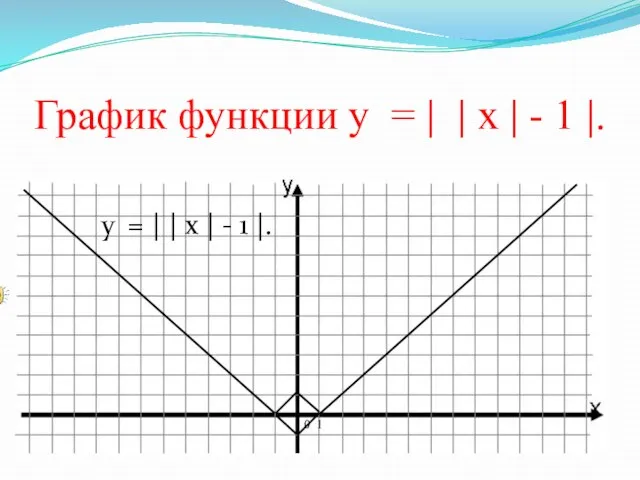
- 17. График функции у = | | х | - 1 |. 0 1 у = |
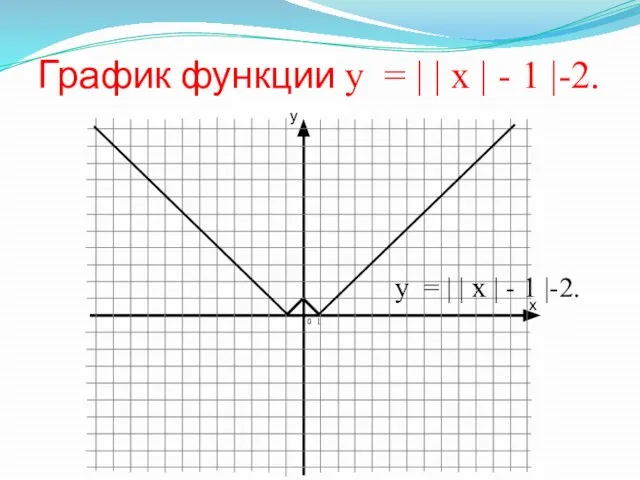
- 18. x y График функции у = | | х | - 1 |-2. 0 1 у
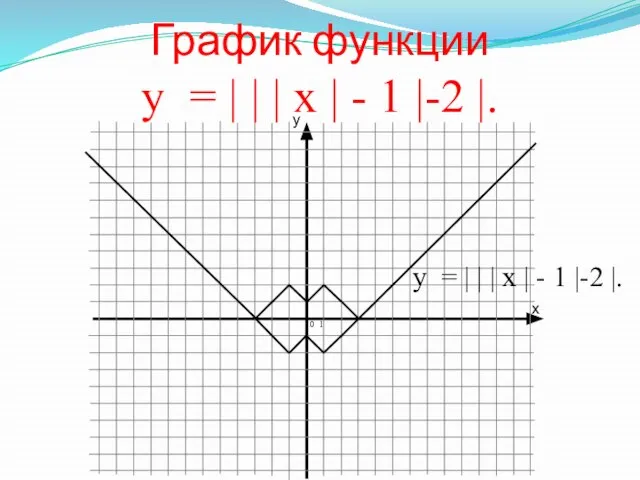
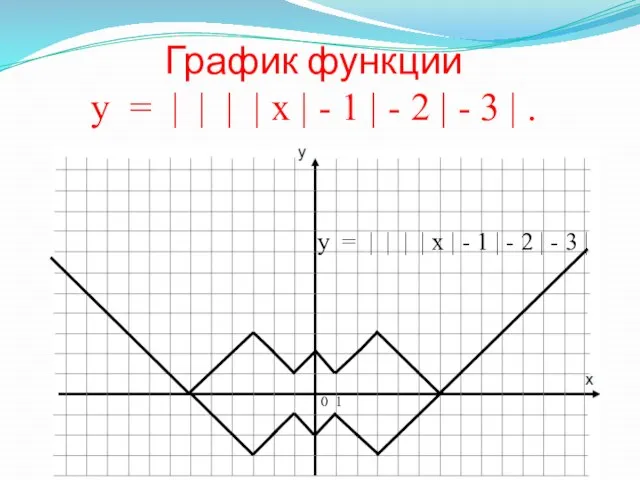
- 19. График функции у = | | | х | - 1 |-2 |. 0 1 у
- 20. График функции у = | | | х | - 1 | - 2 | -
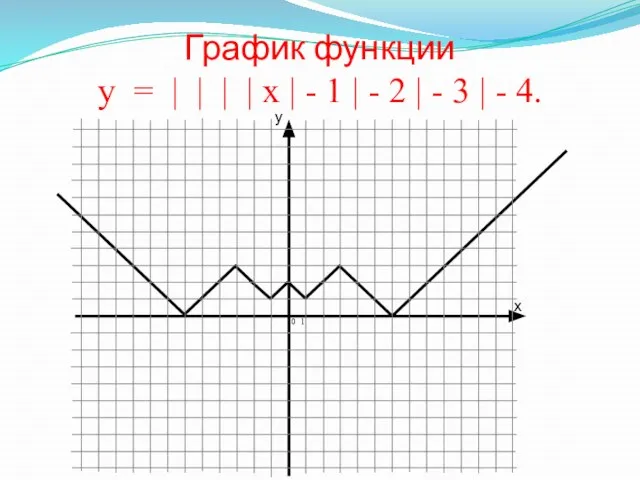
- 21. График функции у = | | | | х | - 1 | - 2 |
- 22. График функции у = | | | | х | - 1 | - 2 |
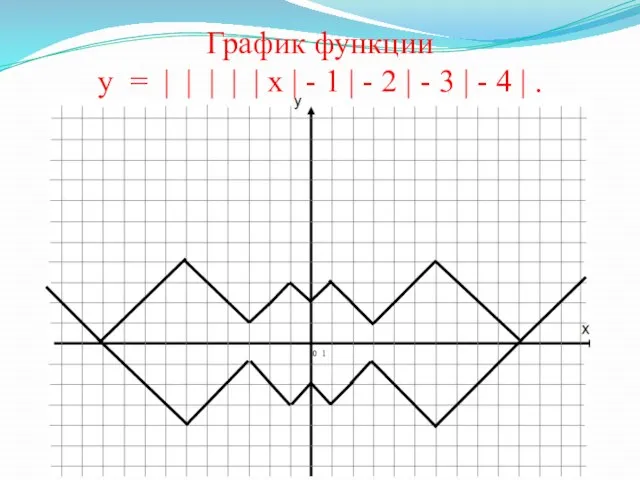
- 23. 0 1 График функции у = | | | | | х | - 1 |
- 25. Скачать презентацию


 Отдых в загородном оздоровительном лагере – это…
Отдых в загородном оздоровительном лагере – это… Учебно-методические комплексы и цифровые образовательные ресурсы по химии как составляющая часть подготовки к ГИА
Учебно-методические комплексы и цифровые образовательные ресурсы по химии как составляющая часть подготовки к ГИА Интерьер – средство создания пространственно-вещной среды интерьера
Интерьер – средство создания пространственно-вещной среды интерьера Staffing the Lodging
Staffing the Lodging История болезни. Клинический диагноз
История болезни. Клинический диагноз Телеканал РБК+
Телеканал РБК+ Книга образов Style book для Натальи Бакулевой. Курс Найди свой стиль
Книга образов Style book для Натальи Бакулевой. Курс Найди свой стиль Проектная деятельность как метод совершенствования коммуникативной компетентности младшего школьника.
Проектная деятельность как метод совершенствования коммуникативной компетентности младшего школьника. Проведение экспертной оценки качества хлеба реализуемого в магазинах торговых сетей Смак
Проведение экспертной оценки качества хлеба реализуемого в магазинах торговых сетей Смак Жизнь и приключения Дятла Вуди
Жизнь и приключения Дятла Вуди Реки Тамбовской области
Реки Тамбовской области Презентация на тему Законы Менделя
Презентация на тему Законы Менделя  Палеозой. Ордовик
Палеозой. Ордовик Школа правовой и финансовой грамотности Основа
Школа правовой и финансовой грамотности Основа Социальные нормы преступность
Социальные нормы преступность Клиника и диагностика хронического панкреатита Докладчик: Цивковский В.Ю. 6 курс, лечебный факультет.
Клиника и диагностика хронического панкреатита Докладчик: Цивковский В.Ю. 6 курс, лечебный факультет. Механизация уплотнения кормов и обработки корнеклубнеплодов
Механизация уплотнения кормов и обработки корнеклубнеплодов Персидская кошка
Персидская кошка BYK Факты & цифры
BYK Факты & цифры Аварийные службы Петербурга
Аварийные службы Петербурга Fit for partnership with Germany
Fit for partnership with Germany Титульный лист кадетка
Титульный лист кадетка Выпуск печатного издания «Наш мир» и оказание полиграфических услуг населению
Выпуск печатного издания «Наш мир» и оказание полиграфических услуг населению Презентация на тему Вредные привычки
Презентация на тему Вредные привычки  Imperfectum onregelmatig Ik val – ik viel
Imperfectum onregelmatig Ik val – ik viel Принципы лечения острых кровотечений
Принципы лечения острых кровотечений Русская-народная сказка Кот, петух и лиса
Русская-народная сказка Кот, петух и лиса Презентация на тему Робототехника и искусственный интеллект
Презентация на тему Робототехника и искусственный интеллект