График тригонометрических функций

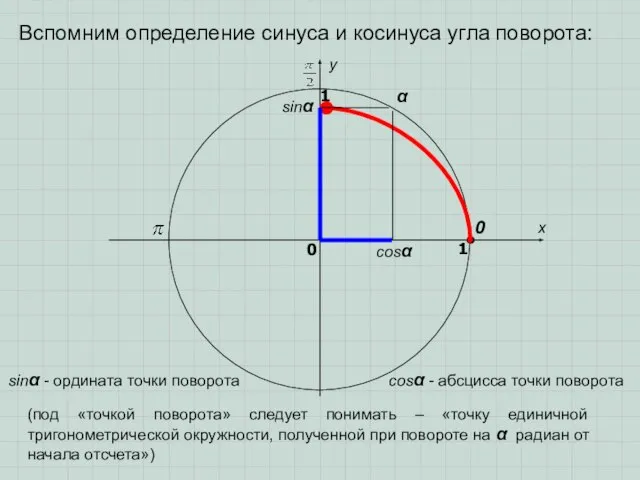
Вспомним определение синуса и косинуса угла поворота:
sinα
cosα
α
x
y
0
1
0
1
sinα - ордината точки поворота
cosα - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на α радиан от начала отсчета»)

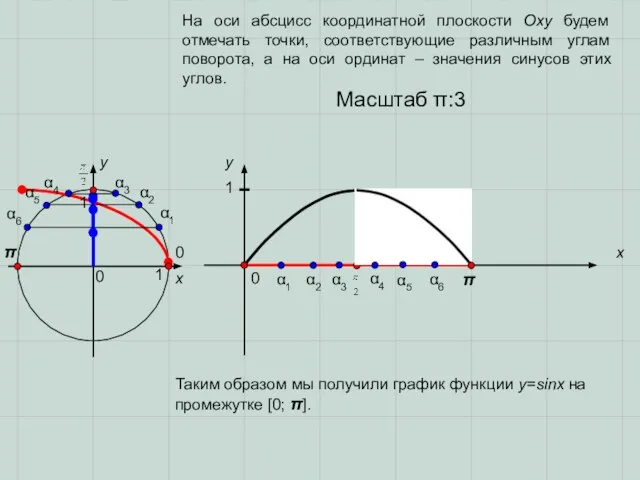
0
0
π
π
x
x
y
y
0
1
1
α1
α2
α3
α3
α2
α1
1
Масштаб π:3
α4
α4
α5
α5
α6
α6
На оси абсцисс координатной плоскости Оху будем отмечать точки, соответствующие различным углам поворота, а на оси ординат – значения синусов этих углов.
Таким образом мы получили график функции y=sinx на промежутке [0; π].

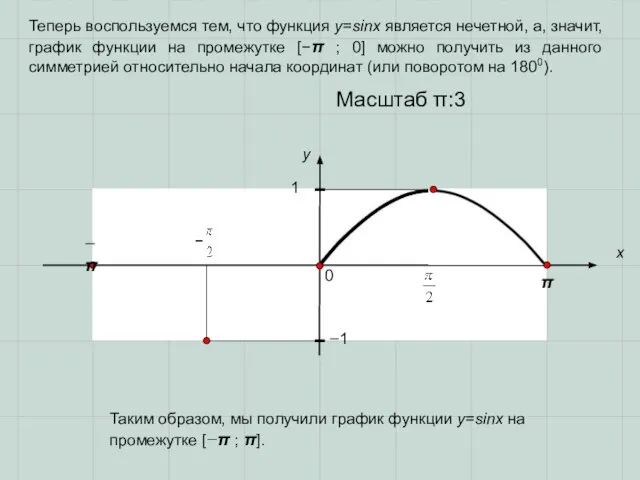
0
π
x
y
1
Масштаб π:3
Таким образом, мы получили график функции y=sinx на промежутке [−π ; π].
−1
−π
Теперь воспользуемся тем, что функция y=sinx является нечетной, а, значит, график функции на промежутке [−π ; 0] можно получить из данного симметрией относительно начала координат (или поворотом на 1800).

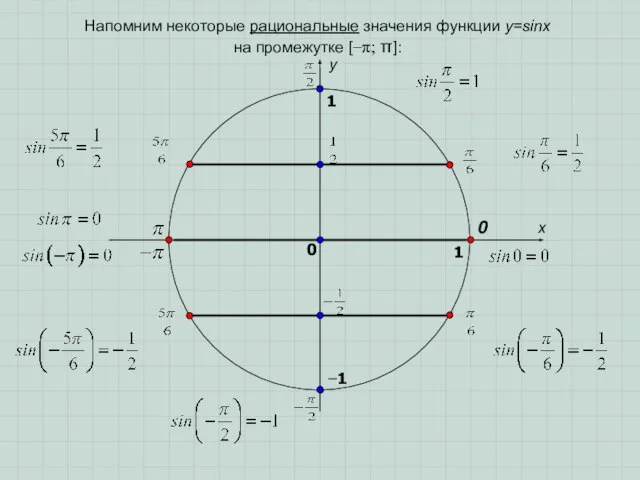
x
y
0
1
0
1
Напомним некоторые рациональные значения функции у=sinx на промежутке [−π; π]:
−1

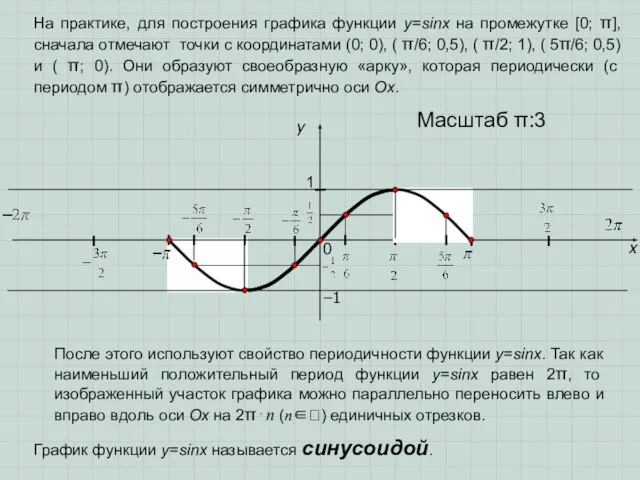
x
y
1
0
Масштаб π:3
На практике, для построения графика функции у=sinx на промежутке [0; π], сначала отмечают точки с координатами (0; 0), ( π/6; 0,5), ( π/2; 1), ( 5π/6; 0,5) и ( π; 0). Они образуют своеобразную «арку», которая периодически (с периодом π) отображается симметрично оси Ох.
После этого используют свойство периодичности функции у=sinx. Так как наименьший положительный период функции y=sinx равен 2π, то изображенный участок графика можно параллельно переносить влево и вправо вдоль оси Ох на 2π⋅n (n∈) единичных отрезков.
−1
График функции y=sinx называется синусоидой.

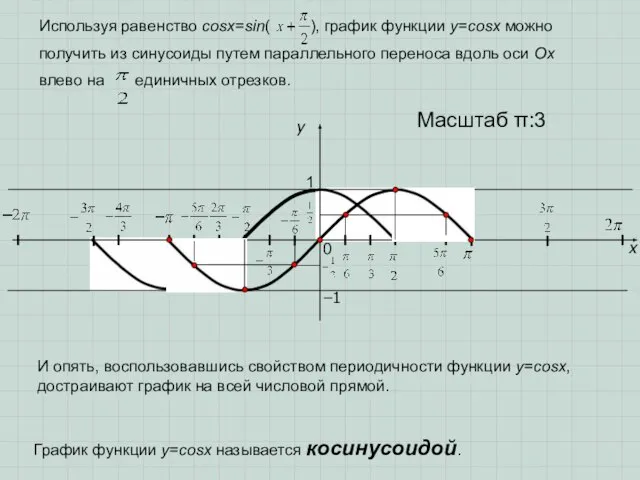
x
y
1
0
Масштаб π:3
−1
Используя равенство cosx=sin( ), график функции у=cosx можно
получить из синусоиды путем параллельного переноса вдоль оси Ох
влево на единичных отрезков.
И опять, воспользовавшись свойством периодичности функции y=cosx, достраивают график на всей числовой прямой.
График функции y=cosx называется косинусоидой.

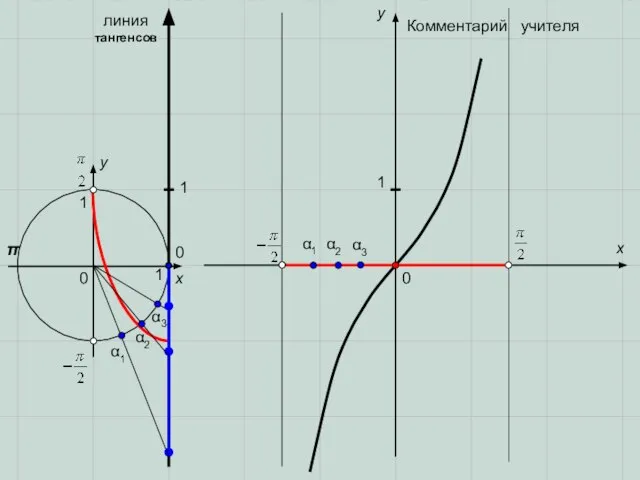
0
0
π
x
x
y
y
0
1
1
α1
α2
α3
α3
α2
α1
1
линия тангенсов
1
Комментарий учителя

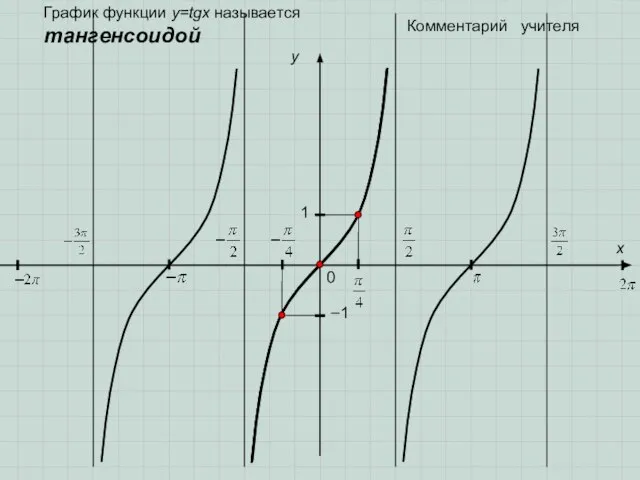
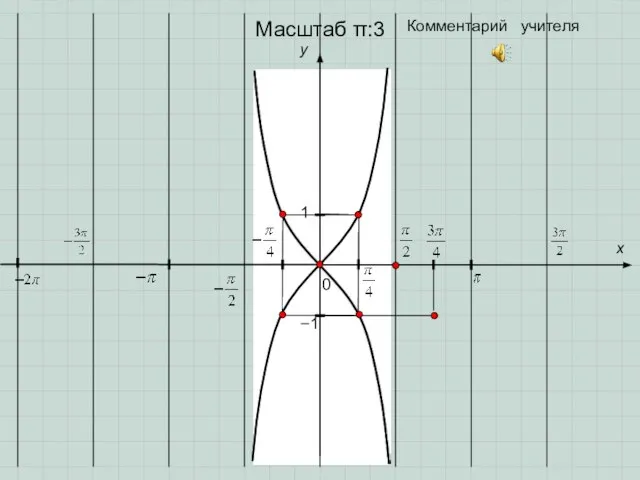
0
y
1
x
−1
Комментарий учителя
График функции y=tgx называется тангенсоидой

0
y
1
x
−1
Комментарий учителя
Масштаб π:3