Характеристика использования систем массового обслуживания и управления рисками в менеджменте. Лекция №9-10
Содержание
- 2. Вопросы: Понятия и определения СМО Метод оценки интенсивности потоков в СМО Модель многоканальной СМО без очереди
- 3. Определения Теория массового обслуживания ~ область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления,
- 4. Определения Заявки в силу массовости поступления на обслуживание образуют потоки, которые до выполнения операций обслуживания называются
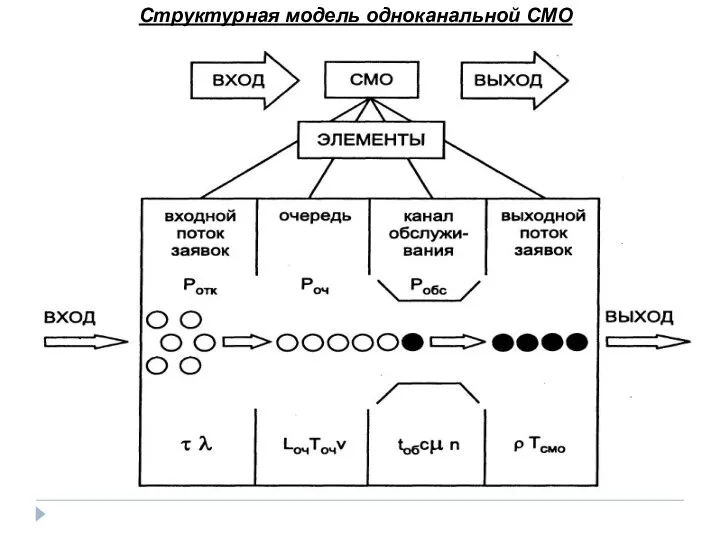
- 5. Структурная модель одноканальной СМО
- 6. Определения Переход СМО из одного состояния в другое происходит случайным образом и представляет собой случайный процесс.
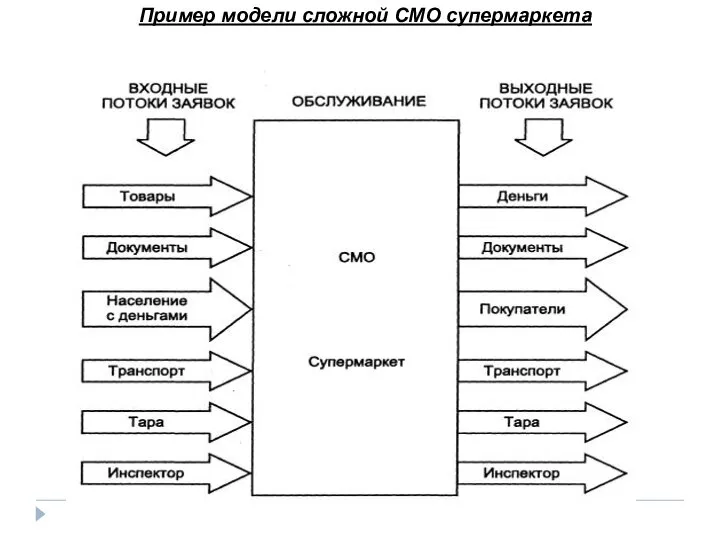
- 7. Пример модели сложной СМО супермаркета
- 8. Определения Переходы СМО из одного состояния в другое происходят под воздействием вполне определенных событий — поступления
- 9. Определения Определения Если поток одновременно обладает свойствами стационарности и ординарности и отсутствием последствия, то такой поток
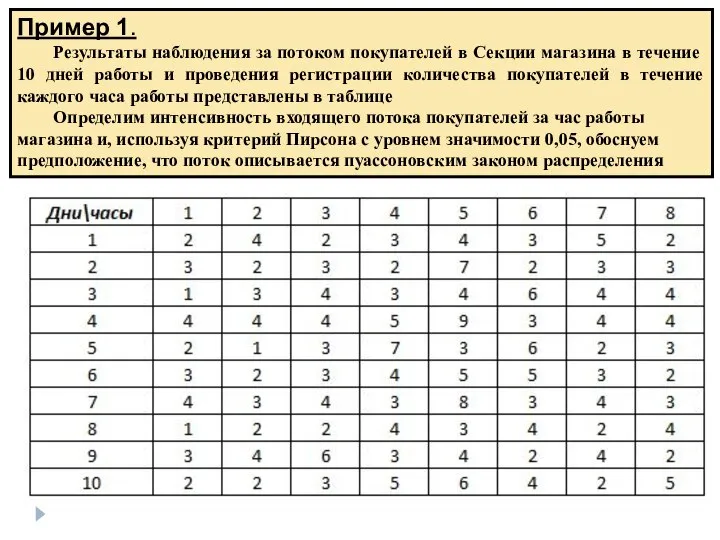
- 10. Пример 1. Результаты наблюдения за потоком покупателей в Секции магазина в течение 10 дней работы и
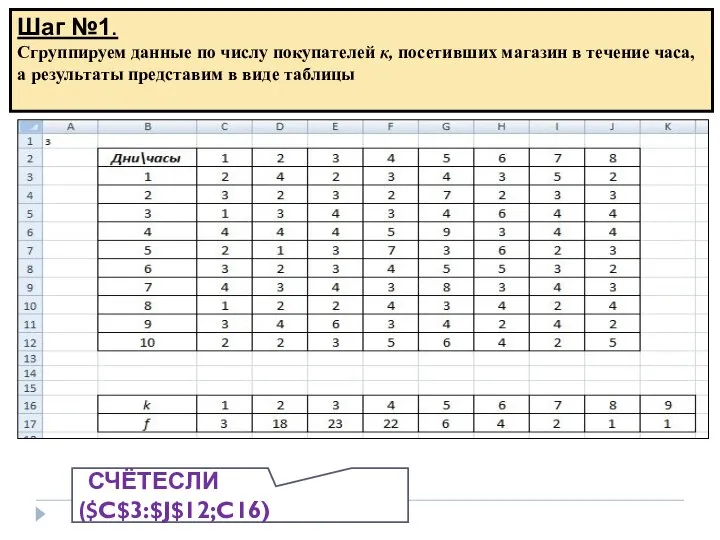
- 11. Шаг №1. Сгруппируем данные по числу покупателей к, посетивших магазин в течение часа, а результаты представим
- 12. Шаг №2. Вычислим интенсивность потока μ = =СУММПРОИЗВ(C16:K16;C17:K17)/СУММ(C17:K17) =СУММ(C17:K17)
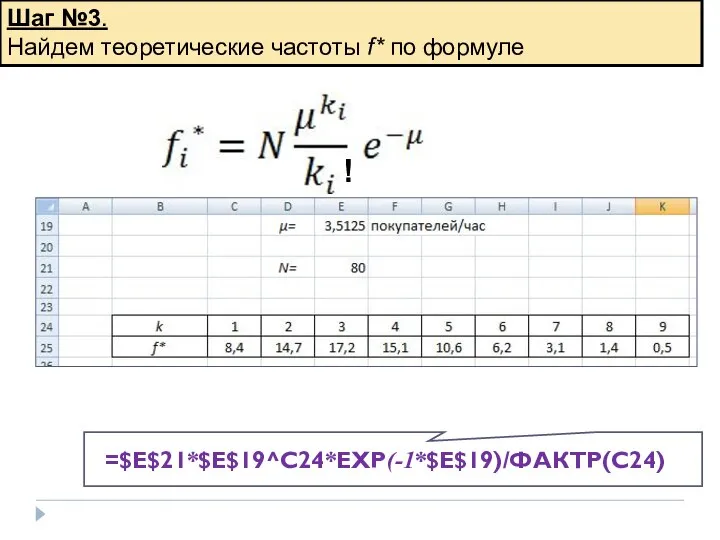
- 13. Шаг №3. Найдем теоретические частоты f* по формуле = =$E$21*$E$19^C24*EXP(-1*$E$19)/ФАКТР(C24) !
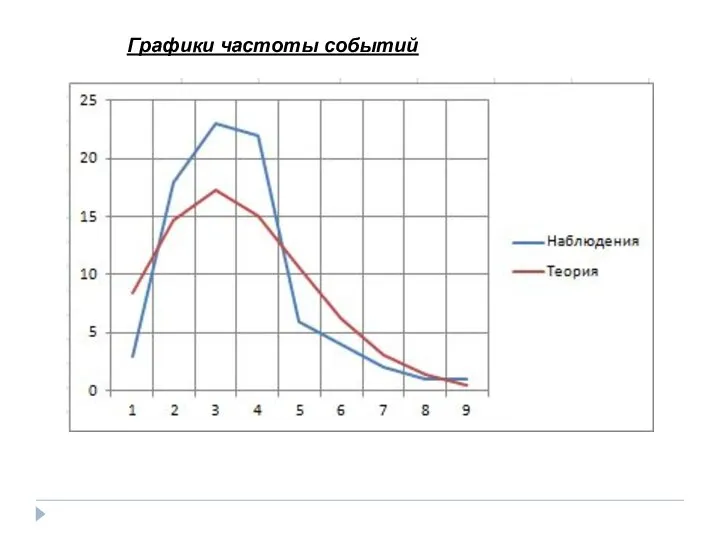
- 14. Графики частоты событий
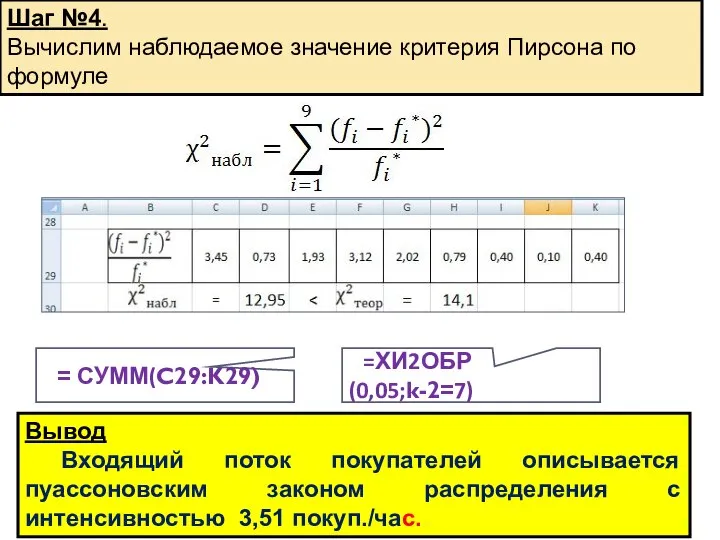
- 15. Шаг №4. Вычислим наблюдаемое значение критерия Пирсона по формуле = = СУММ(C29:K29) = =ХИ2ОБР(0,05;k-2=7) Вывод Входящий
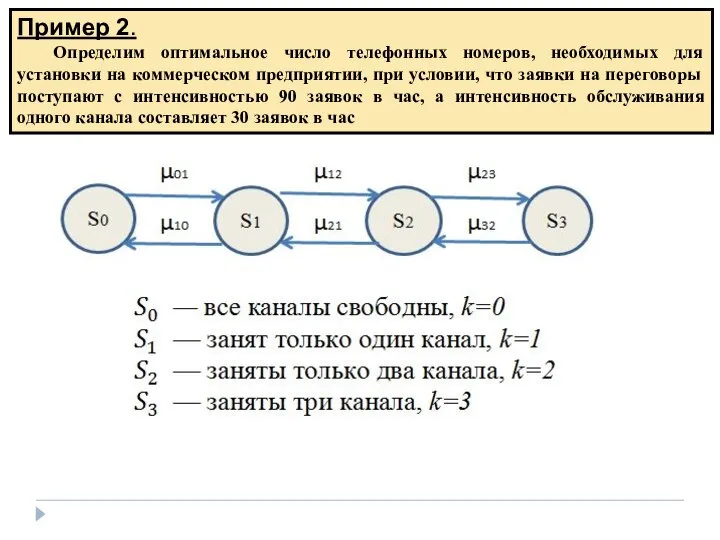
- 16. Пример 2. Определим оптимальное число телефонных номеров, необходимых для установки на коммерческом предприятии, при условии, что
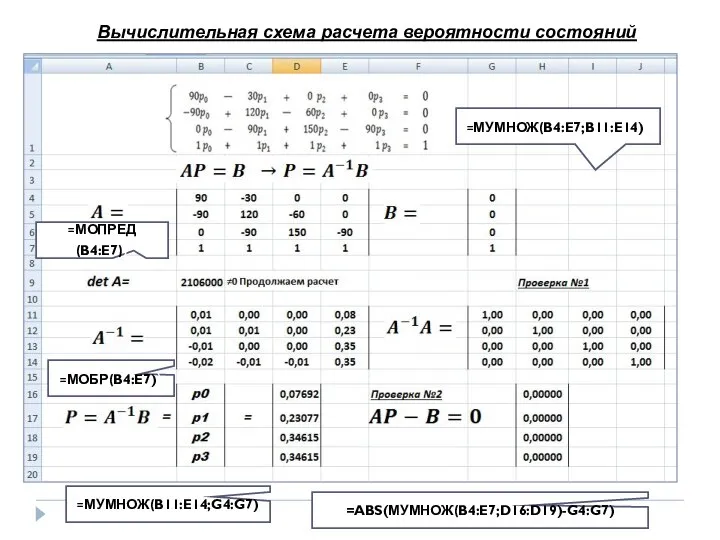
- 18. Вычислительная схема расчета вероятности состояний =МОПРЕД(B4:E7)) =МОБР(B4:E7)) =МУМНОЖ(B4:E7;B11:E14)) =МУМНОЖ(B11:E14;G4:G7) =ABS(МУМНОЖ(B4:E7;D16:D19)-G4:G7)
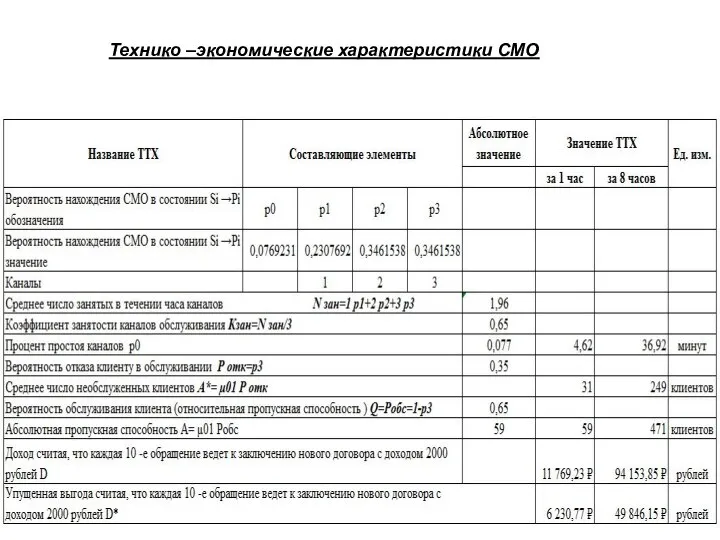
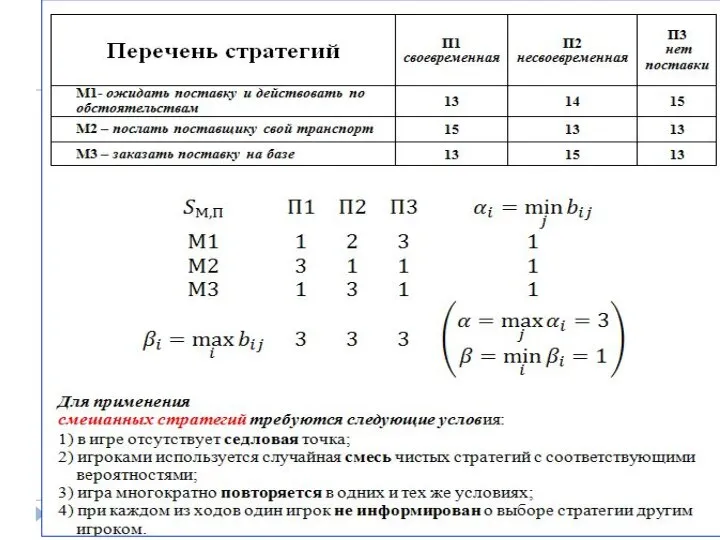
- 19. Технико –экономические характеристики СМО
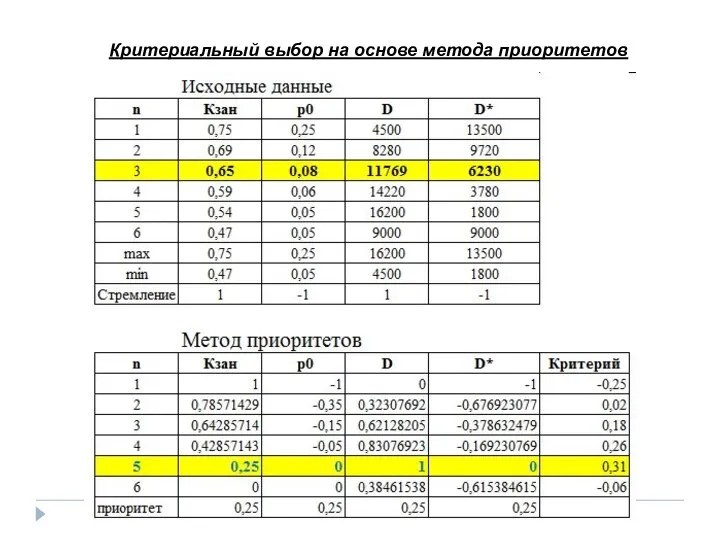
- 20. Критериальный выбор на основе метода приоритетов
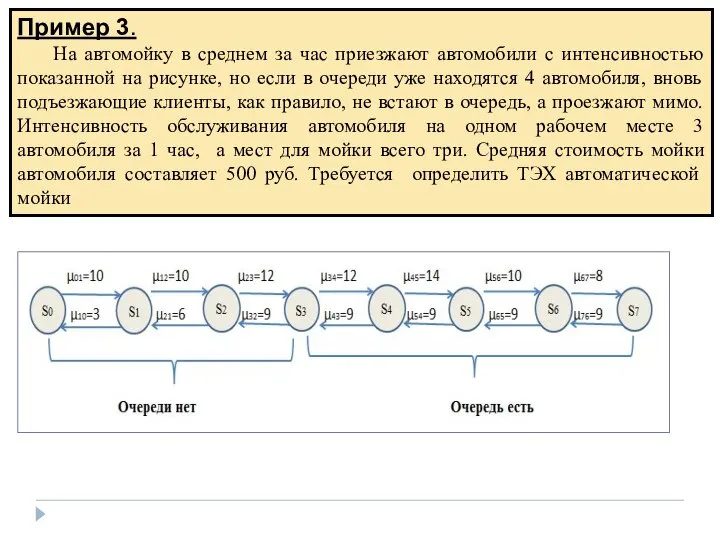
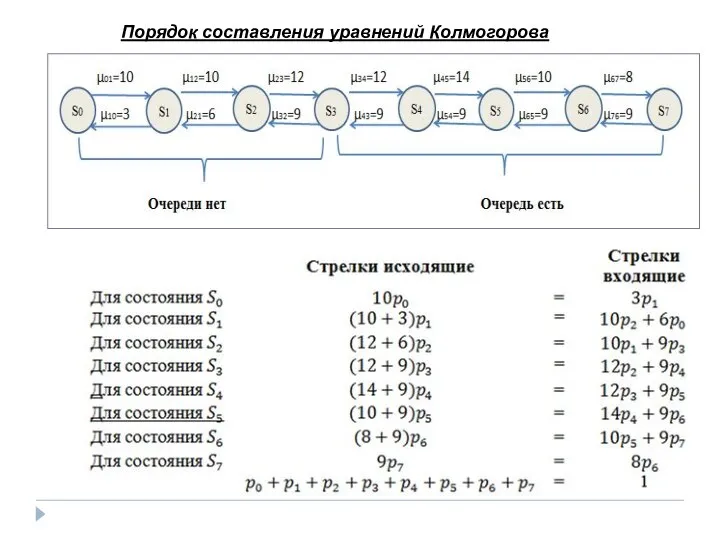
- 21. Пример 3. На автомойку в среднем за час приезжают автомобили с интенсивностью показанной на рисунке, но
- 23. Порядок составления уравнений Колмогорова
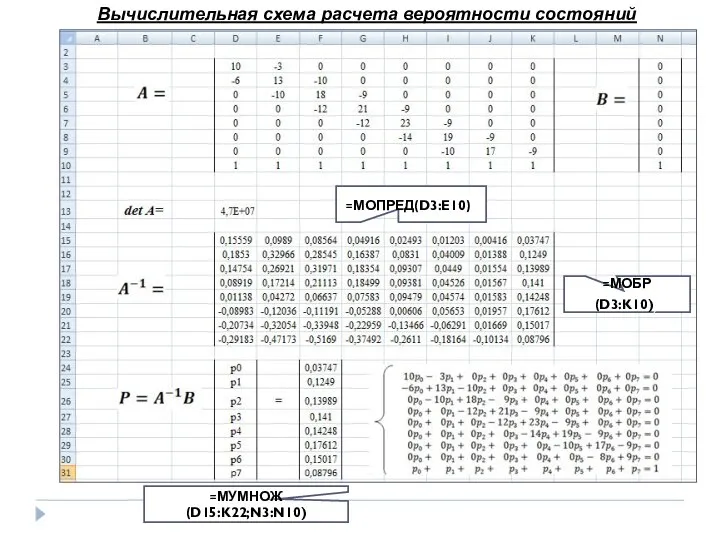
- 25. Вычислительная схема расчета вероятности состояний =МОПРЕД(D3:E10)) =МОБР(D3:K10)) =МУМНОЖ(D15:K22;N3:N10)
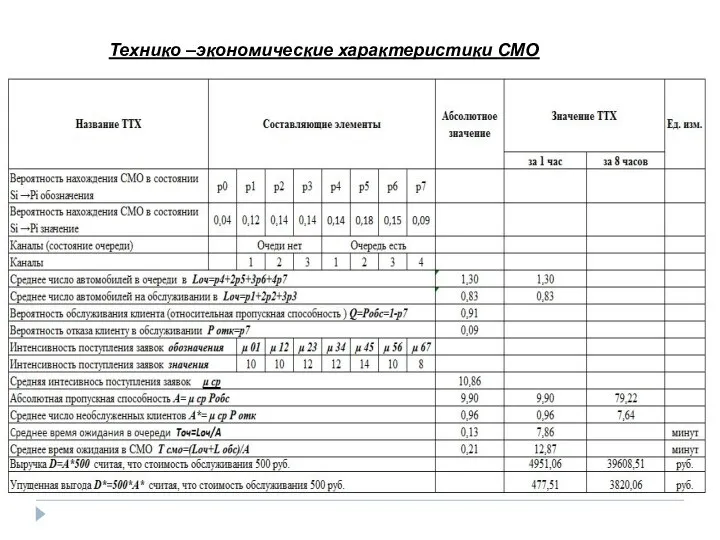
- 26. Технико –экономические характеристики СМО
- 27. Будущее нам неизвестно. А потому неизвестны и будущие доходы и расходы, мы можем лишь прогнозировать их
- 28. Производственные риски. К ним прежде всего относятся риски, связанные с выпуском дефектной продукции. Хорошо известно, что
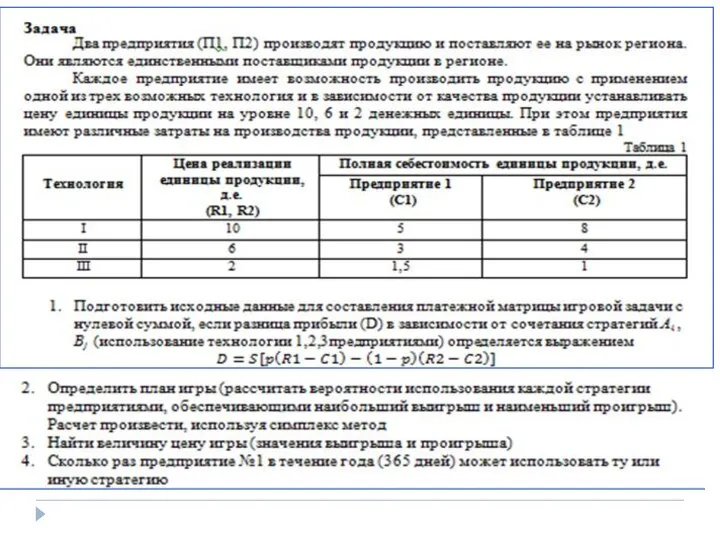
- 29. Описание ситуационного задания
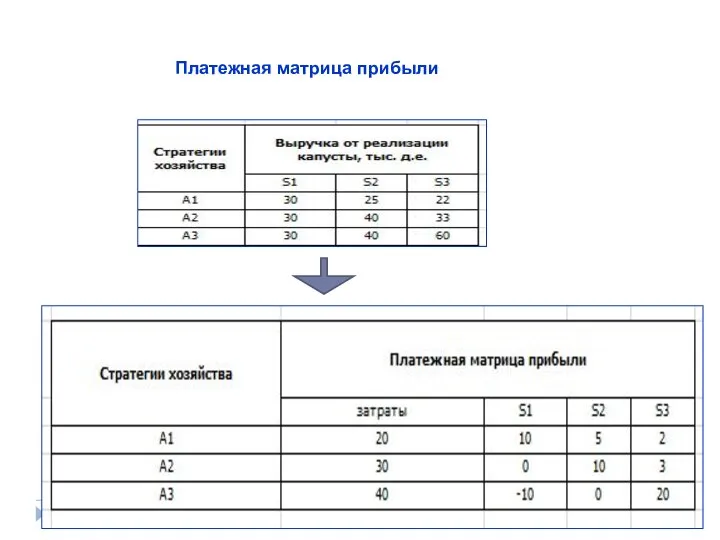
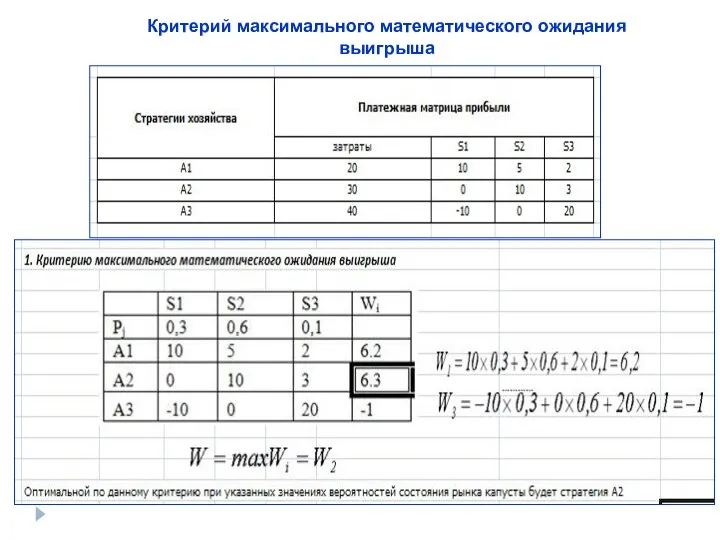
- 30. Платежная матрица прибыли
- 31. Критерий максимального математического ожидания выигрыша
- 32. Критерий Ходжа - Лемана Оптимальной по данному критерию при указанных значениях состояния рынка капусты будет стратегия
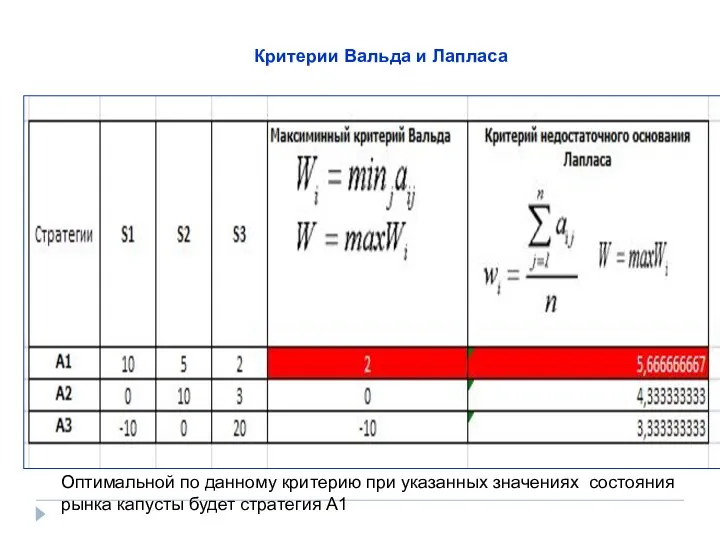
- 33. Критерии Вальда и Лапласа Оптимальной по данному критерию при указанных значениях состояния рынка капусты будет стратегия
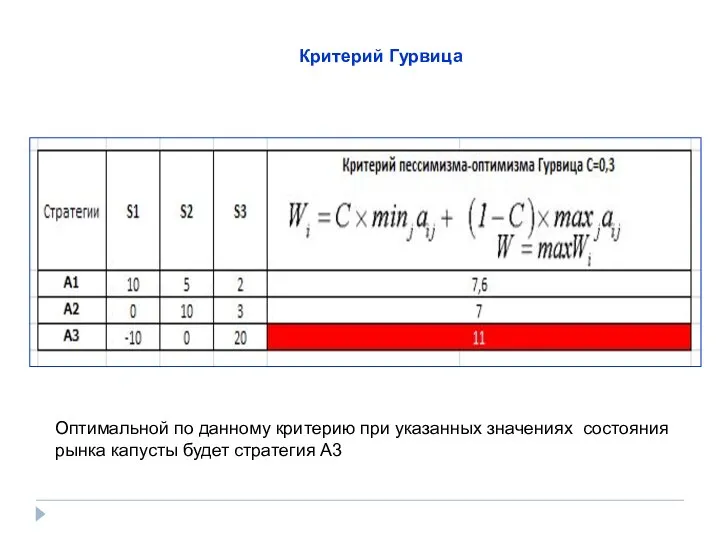
- 34. Критерий Гурвица Оптимальной по данному критерию при указанных значениях состояния рынка капусты будет стратегия A3
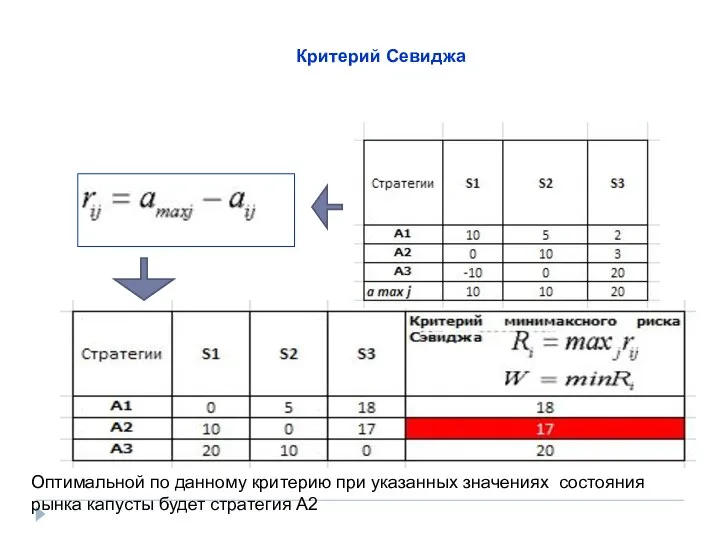
- 35. Критерий Севиджа Оптимальной по данному критерию при указанных значениях состояния рынка капусты будет стратегия A2
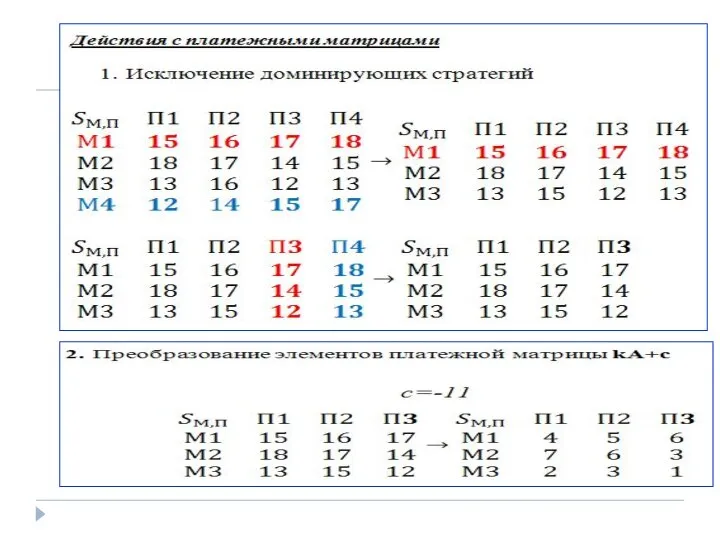
- 40. Основная теорема теории игр Дж. фон Неймана: Каждая конечная игра имеет, по крайней мере, одно оптимальное
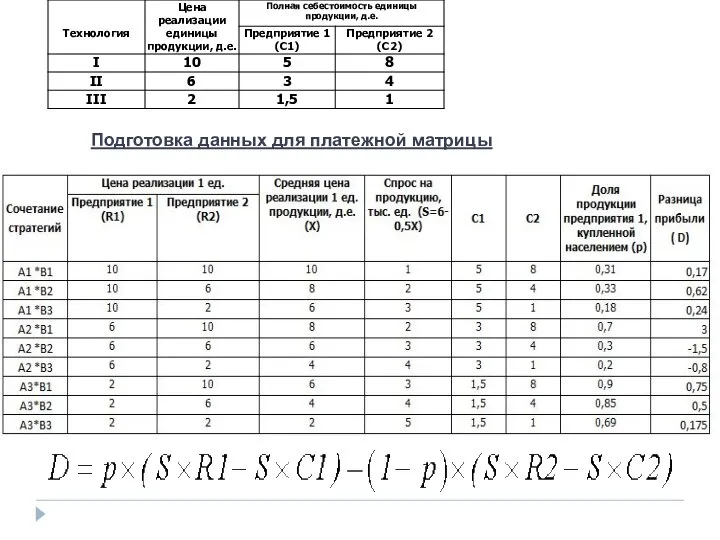
- 42. Подготовка данных для платежной матрицы
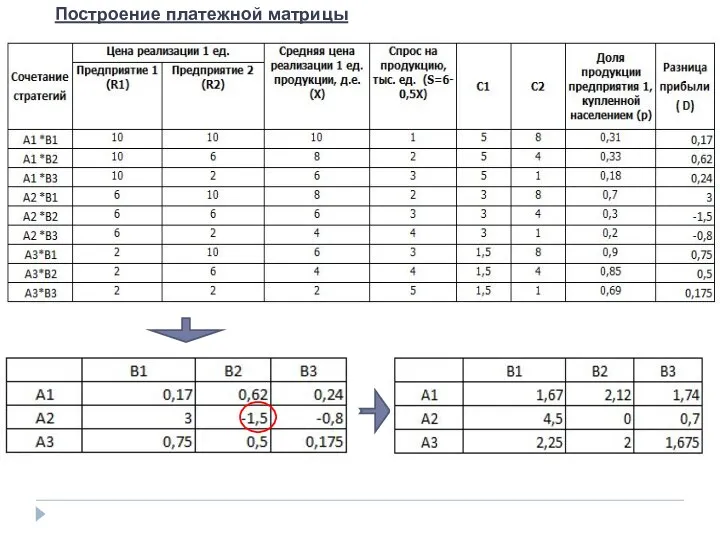
- 43. Построение платежной матрицы
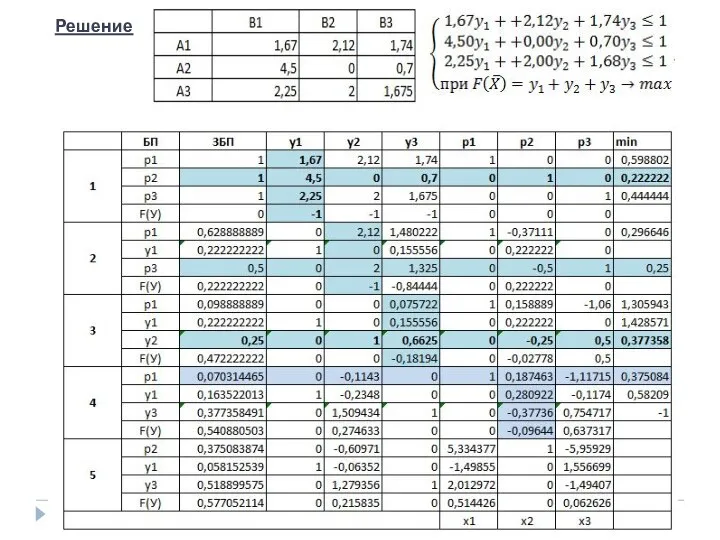
- 45. Решение
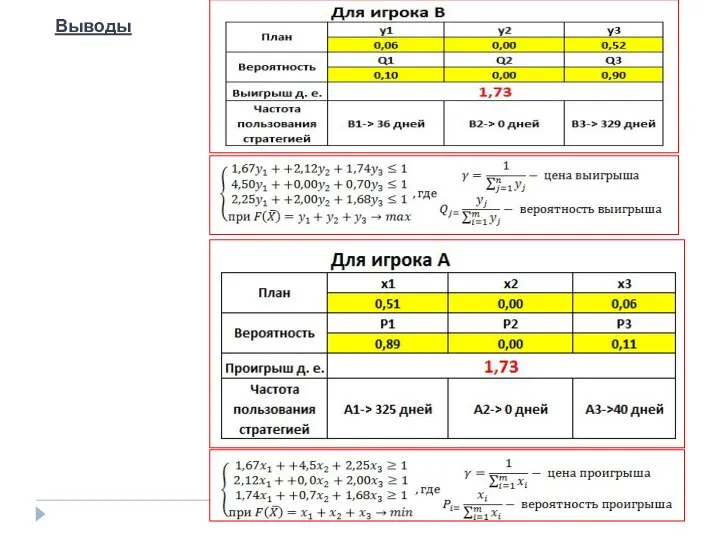
- 46. Выводы
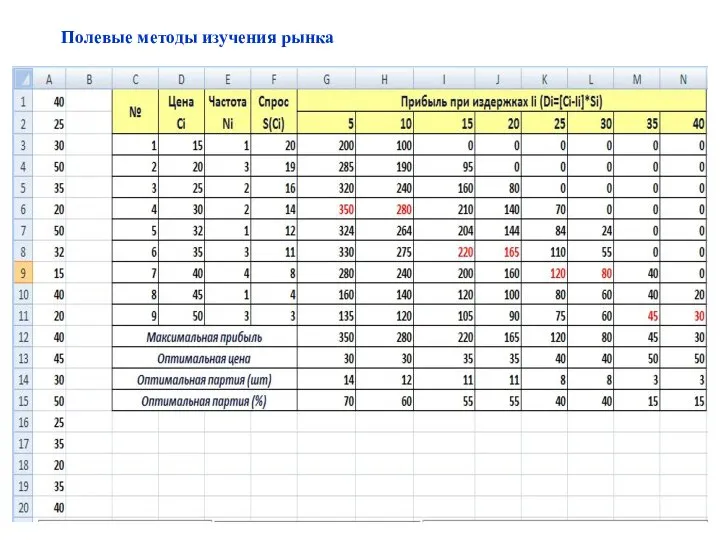
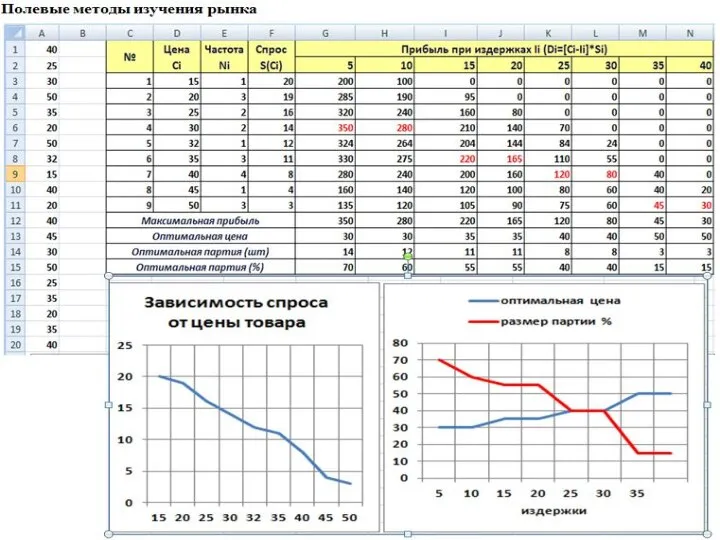
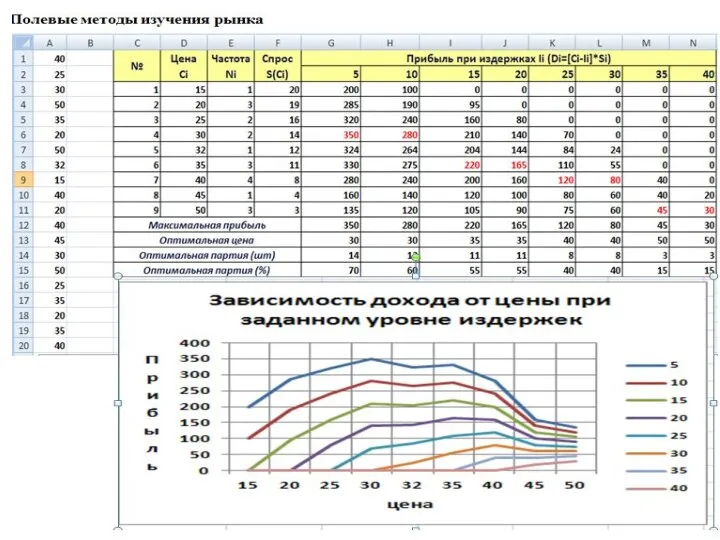
- 47. Полевые методы изучения рынка
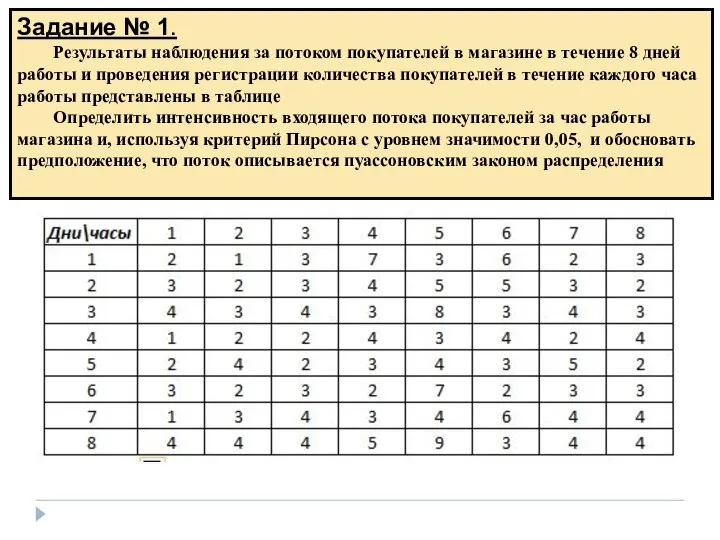
- 50. Задание № 1. Результаты наблюдения за потоком покупателей в магазине в течение 8 дней работы и
- 51. Задание № 2. Определить ТЭХ туристического агентства, имеющего 4- е телефонных номера для приема заявок на
- 52. Задача №4 В Индустриальном районе г. Перми планируется строительство овощехранилища. Имеются три возможных проекта создания такого
- 54. Скачать презентацию




















 Новейшие технологии, средства защиты и очистки атмосферного воздуха от выбросов газа.
Новейшие технологии, средства защиты и очистки атмосферного воздуха от выбросов газа. Title
Title  Портрет. Жанры ИЗО. 3 класс
Портрет. Жанры ИЗО. 3 класс МЕРОПРИЯТИЯ ПРОЕКТА «ШКОЛЬНАЯ СПОРТИВНАЯ ЛИГА» ПРОВЕСТИ В КАЖДОЙ ШКОЛЕ Л.Э. Исаева.
МЕРОПРИЯТИЯ ПРОЕКТА «ШКОЛЬНАЯ СПОРТИВНАЯ ЛИГА» ПРОВЕСТИ В КАЖДОЙ ШКОЛЕ Л.Э. Исаева. Панькина Наталья Михеевна
Панькина Наталья Михеевна Моё хобби
Моё хобби Встреча со Святыней. Сияние Афона
Встреча со Святыней. Сияние Афона Курс: «Социальные коммуникации»
Курс: «Социальные коммуникации» Tuborg НАЦИОНАЛЬНОЕ ПРОМО 2011
Tuborg НАЦИОНАЛЬНОЕ ПРОМО 2011 Презентация на тему Азотная кислота (9 класс)
Презентация на тему Азотная кислота (9 класс) Александр Александрович Дейнека, картина Оборона Севастополя
Александр Александрович Дейнека, картина Оборона Севастополя Шаги для достижения цели
Шаги для достижения цели Инновационная система и политика в РФ
Инновационная система и политика в РФ Презентация на тему Деньги, кредит, банки
Презентация на тему Деньги, кредит, банки  ДИСФОР (ДИалог на языке Структурных ФОРмул)
ДИСФОР (ДИалог на языке Структурных ФОРмул) Организация работы кассовых центровОпыт ОАО «Сбербанк России»
Организация работы кассовых центровОпыт ОАО «Сбербанк России» Презентация на тему Генеалогический метод исследования
Презентация на тему Генеалогический метод исследования  Презентация на тему Организационная структура ФТС России
Презентация на тему Организационная структура ФТС России  Теоретические основы регулирования инвестиционной деятельности в россии. Лекция 1
Теоретические основы регулирования инвестиционной деятельности в россии. Лекция 1 Титан Инжиниринг - проектирование, разработка и строительство энергообъектов. Возможности сотрудничества молодых специалистов
Титан Инжиниринг - проектирование, разработка и строительство энергообъектов. Возможности сотрудничества молодых специалистов Особенности сопровождения детей из различных групп риска
Особенности сопровождения детей из различных групп риска Итоги районной и областной астрономической олимпиады
Итоги районной и областной астрономической олимпиады Экзерсис на середине зала (балет)
Экзерсис на середине зала (балет) И.А. Башмаков Центр по эффективному использованию энергии
И.А. Башмаков Центр по эффективному использованию энергии Бизнес план парикмахерской Лиана
Бизнес план парикмахерской Лиана Оренбургский пуховый платок
Оренбургский пуховый платок Otchet_po_praktike_Serdyukova_A
Otchet_po_praktike_Serdyukova_A Учреждение образования «Белорусский государственный университет физической культуры»
Учреждение образования «Белорусский государственный университет физической культуры»