І. Прямі і площини в просторі ІІ. Многогранники ІІІ. Тіла обертання

Аксіоми стереометрії
Розміщення прямих у просторі
Розміщення площин у просторі
Розміщення прямої і площини в просторі
Перпендикуляр і похила
Прямі і площини в просторі

Многогранники
Пряма призма, площі поверхонь і об'єм прямої призми
Правильна піраміда, площі поверхонь і об'єм правильної піраміди
Призма
Піраміда

Циліндр
Конус
Куля
Тіла обертання
Площі поверхонь і об'єм
Площі поверхонь і об'єм
Площа поверхні і об'єм

Знайдіть стереометричні фігури

1. Яка фігура утворюється внаслідок обертання прямокутника навколо прямої, що містить сторону?
А) призма; Б) куля; В) циліндр; Г) конус .
2. Які дві прямі називаються мимобіжними ?
А) не перетинаються; Б) лежать в різних площинах; В) лежать в різних площинах і не перетинаються; Г) інша відповідь.
3. Як пряма перетинає площину ?
А) в двох точках; Б) в одній точці; В) інша відповідь; Г) три точки.
4. За якою формулою обчислюється площа повної поверхні циліндра?
А) S=2П • R• H; Б) інша відповідь; В) S= 2П • R• H²; Г) S= 2П • R²• H.
5. Яка фігура утворюється внаслідок обертання прямокутного трикутника навколо прямої, що містить катет?
А) призма; Б) інша відповідь; В) циліндр; Г) конус.
6. За якою формулою обчислюється площа бічної поверхні призми?
А) S= Pосн.• H; Б) інша відповідь; В) S= 2Pосн.• H; Г) S= Pосн.• H².
7. За якою формулою обчислюється площа повної поверхні конуса?
А) S=Sосн.+Sбічн.; Б) інша відповідь; В) S= Pосн.+H; Г) S= 2Sосн.+Sбічн.
8. За якою формулою обчислюється об’єм конуса?
А) V= 1/3 Sосн.• H; Б) інша відповідь; В) V= 3Sосн.• H; Г) V=2Sосн.• H.
9. За якою формулою обчислюється площа бічної поверхні піраміди ?
А) S= Pосн.• H; Б) інша відповідь; В) S= Pосн.• L; Г) S=1/2 Pосн.• L.
10. За якою формулою обчислюється об’єм циліндра?
А) V=1/2 Sосн.• H; Б) інша відповідь; В) V= Sосн.• H; Г) V=3Sосн.• H.
Перевіримо, що ви запам'ятали?

11. Яка фігура утворюється внаслідок обертання півкруга навколо діаметра ?
А) куля; Б) інша відповідь; В) сфера; Г) конус.
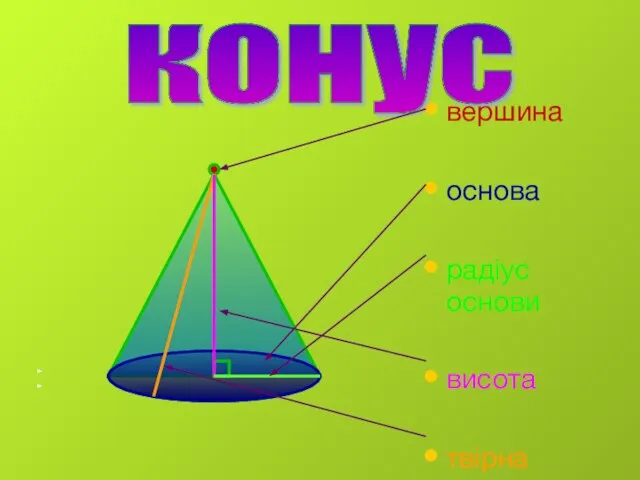
12. За якою формулою обчислюється площа бічної поверхні конуса?
А)S= П • R• L; Б) інша відповідь; В) S= П • R• H; Г) S=2П • R• L.
13. За якою формулою обчислюється площа поверхні кулі?
А)S= П • R• L; Б) інша відповідь; В) S=4П • R²; Г) S= П • R.
14. За якою формулою обчислюється об’єм піраміди?
А) V= Sосн.• H; Б) інша відповідь; В) V=3Sосн. • H; Г) V=1/3 Sосн.• H.
15. За якою формулою обчислюється площа бічної поверхні циліндра?
А) S= П • R• H; Б) інша відповідь; В) S=2П •R• H; Г) S= 1/2 П • R• H.
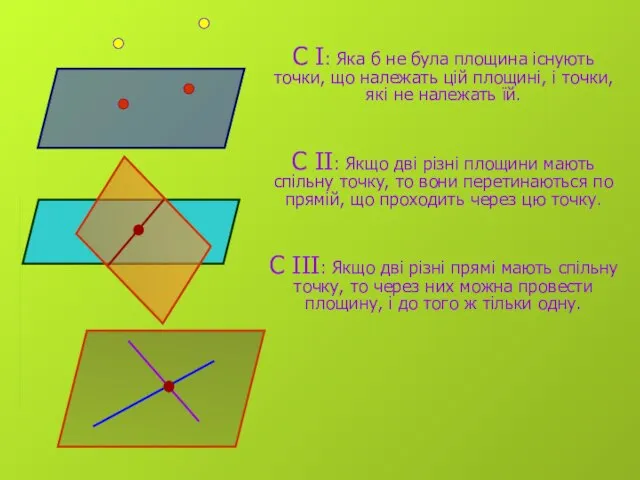
16. Як розташовуються прямі і площини в просторі ?
А) перетинаються; Б) інша відповідь; В) перетинаються, пряма належить площині; Г) перетинаються, пряма належить площині, пряма паралельна площині.
17. Як розташовуються площини в просторі ?
А) перетинаються; Б) інша відповідь; В) перетинаються, паралельні;
Г) паралельні.
18. За якою формулою обчислюється об’єм призми?
А) V= Sосн.• H; Б) інша відповідь; В) V=2Sосн.• H; Г) V=1/2 Sосн.• H.
19. Як розташовуються прямі в просторі ?
А) як завгодно; Б) паралельні , перетинаються, перпендикулярні;
В) паралельні, мимобіжні, перетинаються; Г) перпендикулярні, паралельні, мимобіжні .
20. За якою формулою обчислюється об’єм кулі?
А) S= П • R; Б) інша відповідь; В) S=4/3 П • R³; Г) S=4П • R³.
.
Продовжимо перевіряти, що ви запам'ятали?

С І: Яка б не була площина існують точки, що належать цій площині, і точки, які не належать їй.
С ІІ: Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
С ІІІ: Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

вершина
основа
радіус основи
висота
твірна
конус

SБІЧН.= П •R• L
R- радіус основи
L- твірна
Sповн.=SБІЧН.+ SОСН.
V=1/3• П•R²•H
Площі поверхонь і об'єм

Центр
Радіус
Діаметр
Куля

sк=4•П• R²
R-радіус кулі
V=4/3•П•R³
Площа поверхні і об'єм