И ВЫСОТА

Две прямые, которые пересекаются под прямым углом называются перпендикулярными

Перпендикуляром к данной прямой называют отрезок прямой перпендикулярной данной, один конец, которого – точка пересечения этих прямых.
a
b
b
O
A
a ┴ b, ОА – перпендикуляр
т О – основание перпендикуляра

Теорема: из точки не лежащей на данной прямой можно провести перпендикуляр к этой прямой и при том только один.

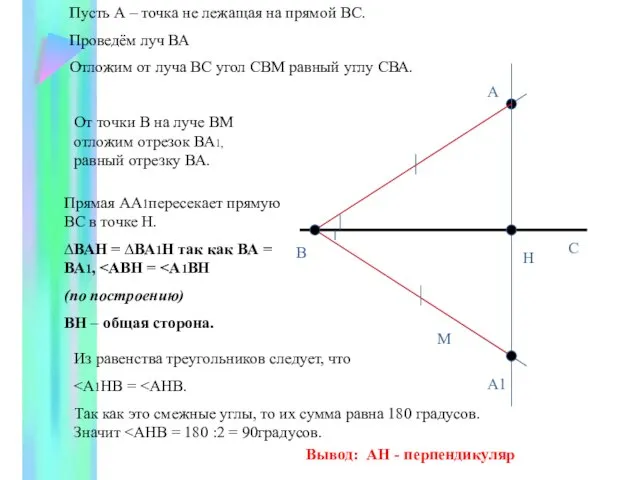
А
В
М
Пусть А – точка не лежащая на прямой ВС.
Проведём луч ВА
Отложим от луча ВС угол СВМ равный углу СВА.
С
От точки В на луче ВМ отложим отрезок ВА1, равный отрезку ВА.
А1
Н
Прямая АА1пересекает прямую ВС в точке Н.
∆ВАН = ∆ВА1Н так как ВА = ВА1, <АВН = <А1ВН
(по построению)
ВН – общая сторона.
Из равенства треугольников следует, что
Так как это смежные углы, то их сумма равна 180 градусов. Значит <АНВ = 180 :2 = 90градусов.
Вывод: АН - перпендикуляр

а
А
Докажем, что из точки А на прямую можно опустить только один перпендикуляр.
Если предположить, что из точки А можно опустить ещё один перпендикуляр АН1к данной прямой.
Н
Н1
Получится, что Прямые АН и АН1перпендикулярные одной прямой пересекаются в точке А.
ОДНАКО, мы уже доказывали ранее, что это невозможно, две прямые перпендикулярны третьей прямой не пересекаются.
ВЫВОД: из точки А на прямую можно опустить только один перепендикуляр!

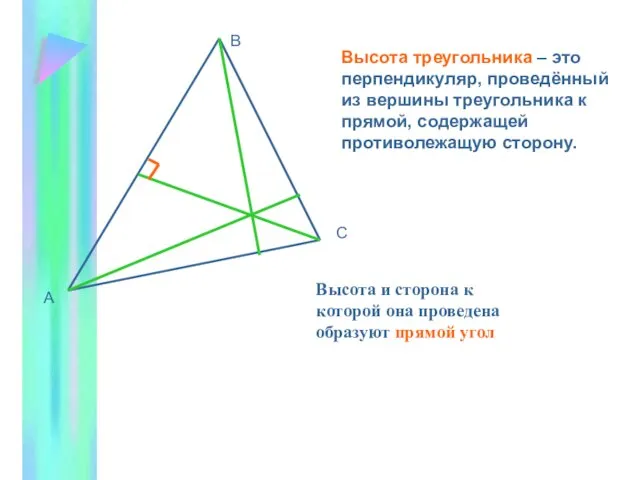
А
В
С
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
Высота и сторона к которой она проведена образуют прямой угол

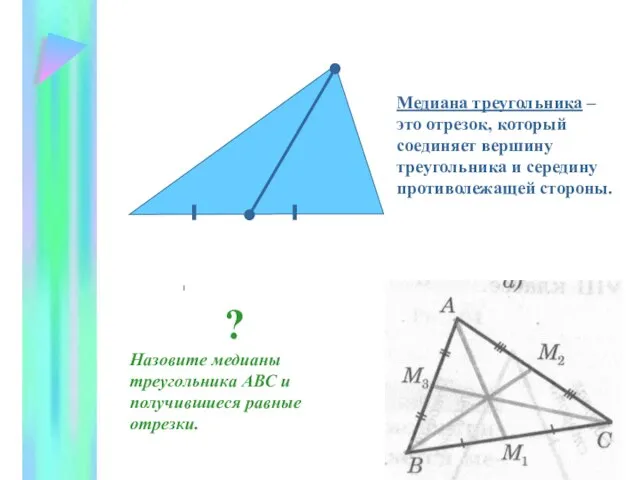
Медиана треугольника – это отрезок, который соединяет вершину треугольника и середину противолежащей стороны.
Назовите медианы треугольника АВС и получившиеся равные отрезки.
?

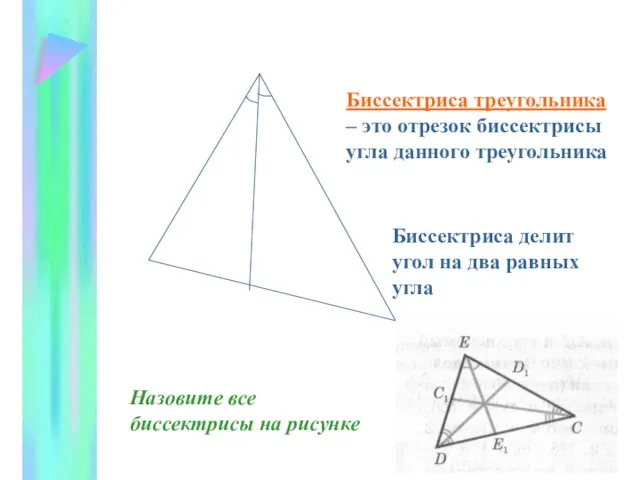
Биссектриса треугольника – это отрезок биссектрисы угла данного треугольника
Биссектриса делит угол на два равных угла
Назовите все биссектрисы на рисунке