Содержание
- 2. Пусть существуют два множества: Множество объектов – образов X Множество ответов Y Существует целевая функция значения
- 3. Модель алгоритма Требуется построить отображение (гипотезу) Пусть А – параметрическое семейство отображений Г – пространство допустимых
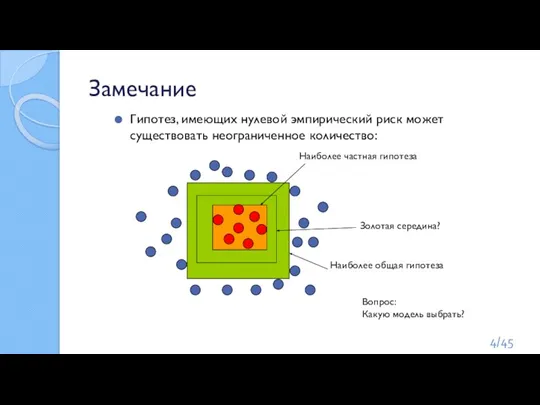
- 4. Замечание Гипотез, имеющих нулевой эмпирический риск может существовать неограниченное количество: Наиболее общая гипотеза Наиболее частная гипотеза
- 5. Эмпирический риск - обучающая выборка Эмпирический риск (ошибка тренировки): Метод минимизации эмпирического риска*: Таким образом задача
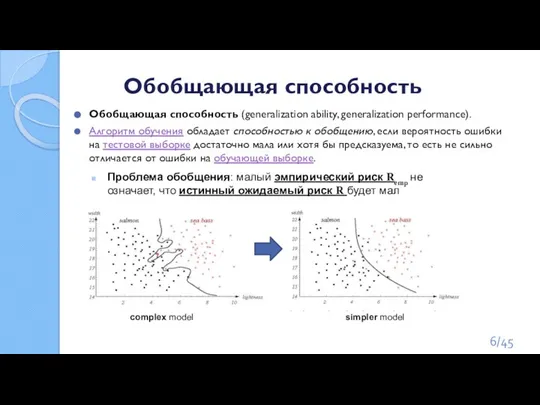
- 6. Обобщающая способность Обобщающая способность (generalization ability, generalization performance). Алгоритм обучения обладает способностью к обобщению, если вероятность
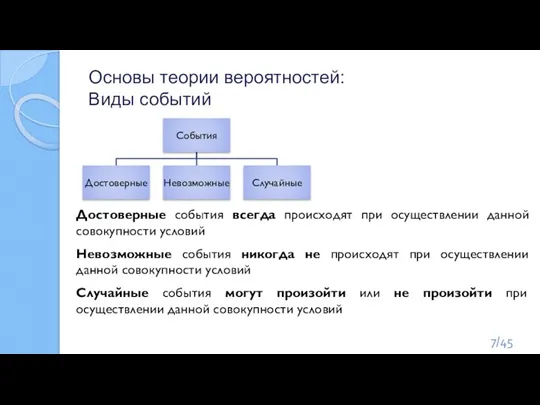
- 7. Основы теории вероятностей: Виды событий Достоверные события всегда происходят при осуществлении данной совокупности условий Невозможные события
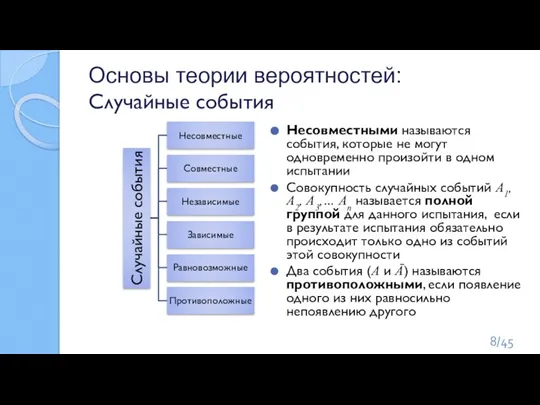
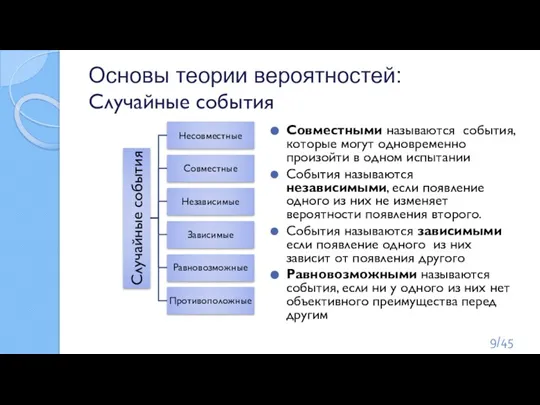
- 8. Основы теории вероятностей: Случайные события Несовместными называются события, которые не могут одновременно произойти в одном испытании
- 9. Основы теории вероятностей: Случайные события Совместными называются события, которые могут одновременно произойти в одном испытании События
- 10. Основы теории вероятностей: Классическое определение вероятности Вероятностью события А называют отношение числа благоприятствующих этому событию элементарных
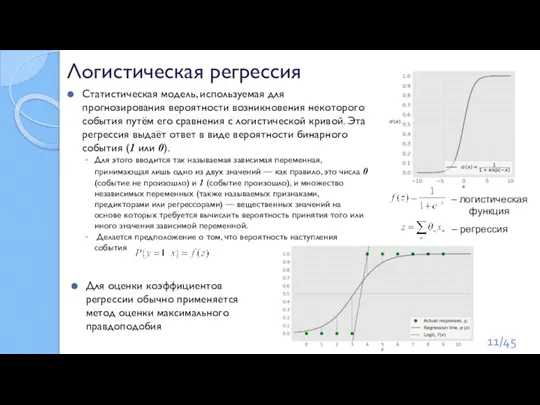
- 11. Статистическая модель, используемая для прогнозирования вероятности возникновения некоторого события путём его сравнения с логистической кривой. Эта
- 12. Thomas Bayes (c. 1702 – April 17, 1761) Томас Байес Математические интересы Байеса относились к теории
- 13. Определение. Пусть Р(А)>0. Условной вероятностью Р(В/А) события В при условии, что событие А наступило, называется число
- 14. Независимые события Определение. События А и В называются независимыми, если Определение. Пусть Р(А)>0 и Р(В)>0. Событие
- 15. События образуют полную группу, если они 1) попарно несовместны 2) в результате эксперимента обязательно какое- либо
- 16. Формула полной вероятности Теорема. Если события образуют полную группу , то для любого события А справедлива
- 17. Формула Байеса Теорема. Пусть события образуют полную группу. Пусть событие А наступило ( Р(А)>0 ). Тогда
- 18. Формула Байеса. Частный случай Рассмотрим события они образуют полную группу. Пусть событие А наступило ( Р(А)>0
- 19. Пример: Какова вероятность увидеть на улице динозавра? Идя по улице вы видите такую сцену: Правдоподобие –
- 20. Пример: Какова вероятность увидеть на улице динозавра? Идя по улице вы видите такую сцену: Правдоподобие –
- 21. Вероятностная формулировка задачи машинного обучения Эмпирический риск: Общий риск: рассчитать невозможно требуется минимизировать Модель алгоритма и
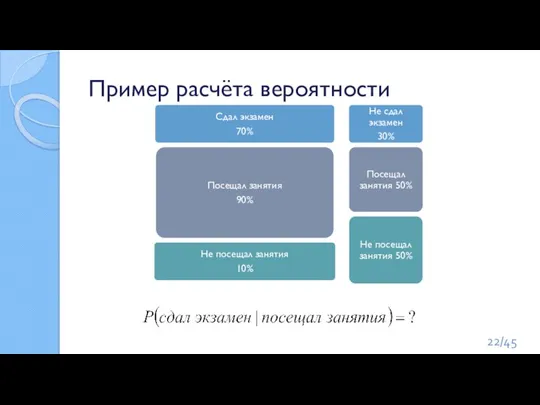
- 22. Пример расчёта вероятности /45
- 23. Пример расчёта вероятности /45
- 24. Пример расчёта вероятности /45
- 25. Домашнее задание 1: Пример расчёта вероятности Пусть некий тест на какую-нибудь болезнь имеет вероятность успеха 95%
- 26. Наивный байесовский классификатор Предположения: Известна функция правдоподобия: Известны априорные вероятности: Принцип максимума апостериорной вероятности: Вероятность класса
- 27. Example. Play Tennis x=(Sunny, Cool, High, Strong) /45
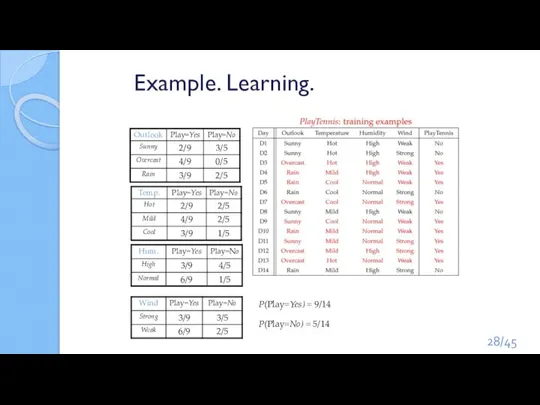
- 28. Example. Learning. P(Play=Yes) = 9/14 P(Play=No) = 5/14 /45
- 29. Example.Test x=(Outlook=Sunny, Temperature=Cool, Humidity=High, Wind=Strong) P(Outlook=Sunny|Play=No) = 3/5 P(Temperature=Cool|Play==No) = 1/5 P(Huminity=High|Play=No) = 4/5 P(Wind=Strong|Play=No) =
- 30. Особенности наивного байесовского классификатора Нужно знать функцию правдоподобия и априорные вероятности Отсутствуют априорные причины верить, что
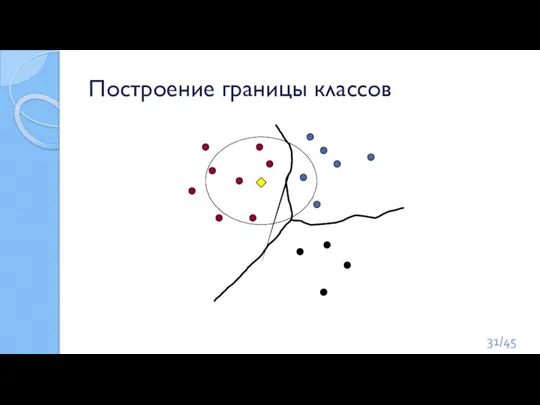
- 31. Построение границы классов /45
- 32. Разбиение пространства, как задача классификации Задача классификации: определить вектор x в один из K классов Y
- 33. Разделение на несколько классов Классифицируем в Yk если соответствующий yk – максимален Можно рассмотреть поверхности вида
- 34. Задача линейной регрессии Нужно найти функцию, которая отображает зависимость одних переменных или данных от других. Зависимые
- 35. Задача линейной регрессии Через две точки на плоскости можно провести прямую и только одну А если
- 36. Scikit-learn Библиотека Scikit-learn — самый распространённый выбор для решения задач классического машинного обучения. Scikit-learn специализируется на
- 37. Scikit-learn Вход-выход (x-y) (зелёные круги) – результаты наблюдений. Оценочная функция регрессии (чёрная линия) выражается уравнением f(x)
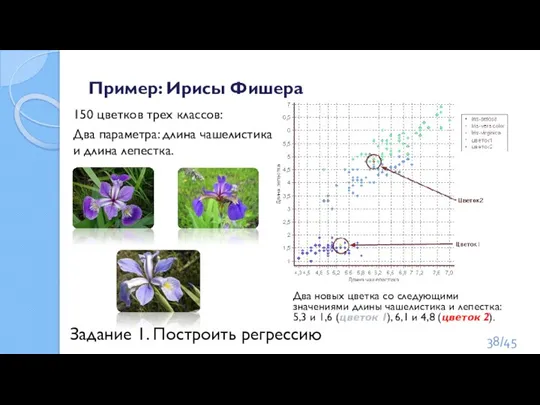
- 38. Пример: Ирисы Фишера 150 цветков трех классов: Два параметра: длина чашелистика и длина лепестка. Два новых
- 39. Метод «k-ближайших соседей». Классификатор K-nearest neighbor – kNN Метод решения задачи классификации, который относит объекты к
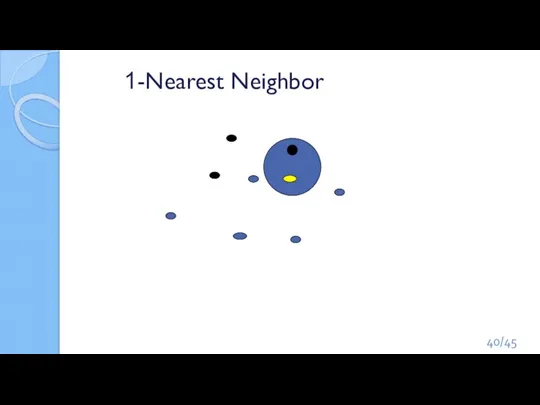
- 40. 1-Nearest Neighbor /45
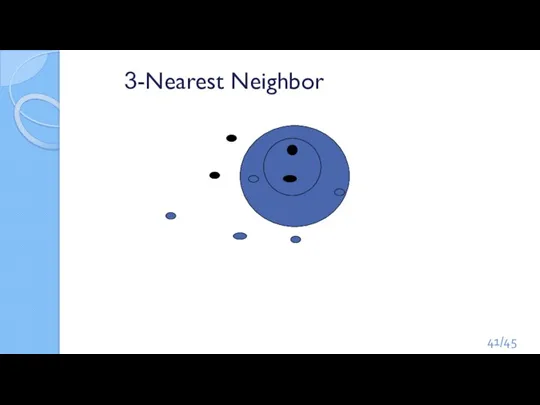
- 41. 3-Nearest Neighbor /45
- 42. Нормализация и вычисление расстояния Расстояние Махаланобиса Евклидово расстояние Предложено индийским статистиком Махаланобисом в 1936 году. С
- 43. Ирисы Фишера: Простое голосование Класс цветка 1: Iris Setosa /45
- 44. Ирисы Фишера: Простое голосование Класс цветка 2: Iris Virginica /45
- 46. Скачать презентацию































 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края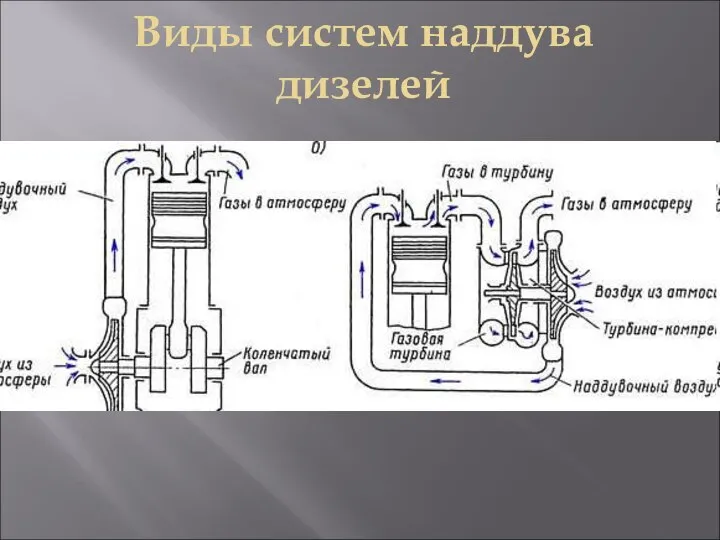 Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной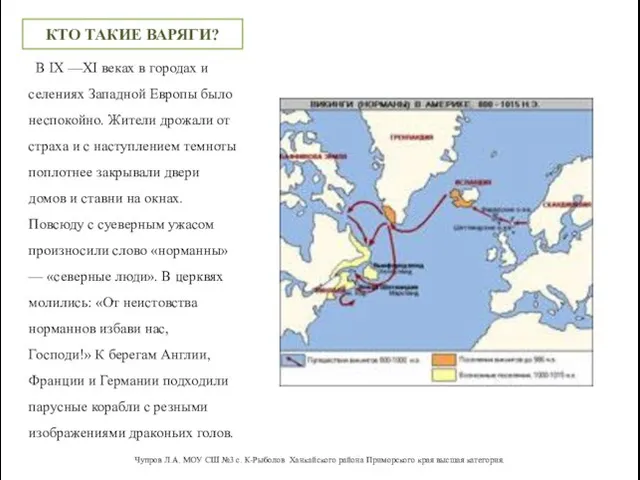 Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота