Содержание
- 2. Часть 0 – Предисловие
- 3. Часть I - Введение Область применения Постановка задачи Примеры Имеющиеся результаты
- 4. Область применения Необходимость поиска с учетом ошибок: Поиск документов в Интернете Автоматическое исправление орфографических ошибок Вычислительная
- 5. Постановка задачи (1) Коллекция документов Т суммарного размера n Образец P длины m Предполагается не более
- 6. Постановка задачи (2) Требуется найти Все вхождения Все начальные позиции вхождений Все документы, содержащие образец
- 7. Пример Документы: GACTCAAAACGGGTGC GTGACCGACGGATGAC CCTACAAACATGTTCG TAAACCTGAGACCAAC Образец: ACAAC Разрешенное число ошибок: d = 1
- 8. Пример Документы: GACTCAAAACGGGTGC GTGACCGACGGATGAC CCTACAAACATGTTCG TAAACCTGAGACCAAC Образец: ACAAC Разрешенное число ошибок: d = 1 Различные вхождения:
- 9. Пример Документы: GACTCAAAACGGGTGC GTGACCGACGGATGAC CCTACAAACATGTTCG TAAACCTGAGACCAAC Образец: ACAAC Разрешенное число ошибок: d = 1 Начальные позиции
- 10. Пример Документы: GACTCAAAACGGGTGC GTGACCGACGGATGAC CCTACAAACATGTTCG TAAACCTGAGACCAAC Образец: ACAAC Разрешенное число ошибок: d = 1 Документы, содержащие
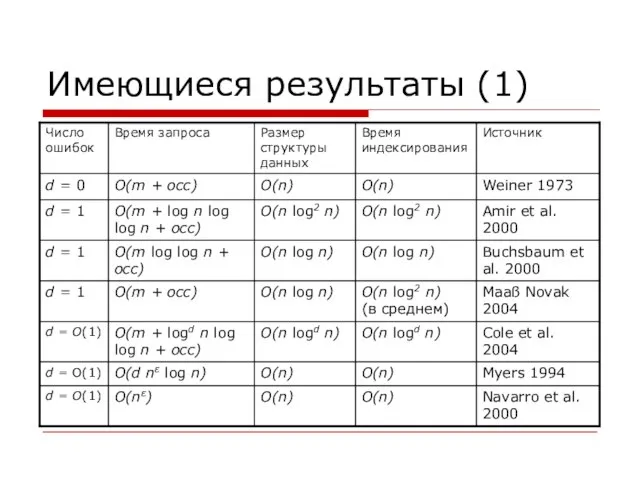
- 11. Имеющиеся результаты (1)
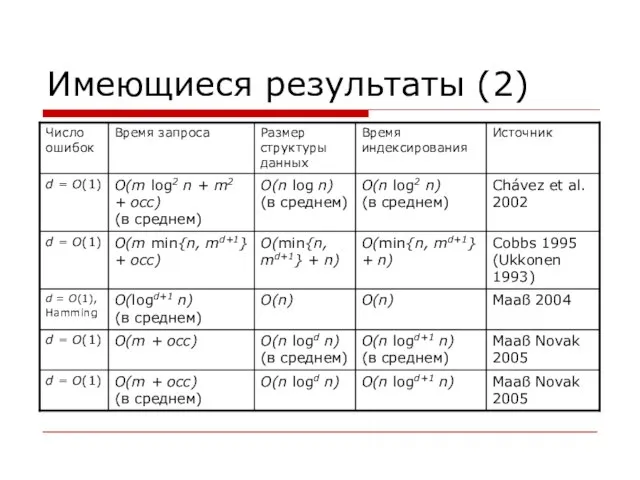
- 12. Имеющиеся результаты (2)
- 13. Часть II – Необходимые знания Расстояние Левенштейна Функция minpref Бор Сжатый бор l-слабый бор Интервальные запросы
- 14. Расстояние Левенштейна d(u,v) = наименьшее количество операций редактирования, необходимое, чтобы перевести u в v. Вычисляется методом
- 15. Расстояние Левенштейна (2) Пример: d(”АВТОР”, ”АФФТАР”) = 3 АВТОР АФТОР АФФТОР АФФТАР За время O((|u|+|v|)*k) можно
- 16. Функция minprefu(v) minprefu(v) = min l: d(prefl(u),prefl+|u|-|v|(v)) = d(u,v) suffl+1(u) = suffl+|u|-|v|+1(v) Пример: minpref”АВТОР”(”АФФТАР”) = 4
- 17. Лемма о minpref Пусть d(u,v)=k Обозначим за u(i) строку u после i из k операций редактирования
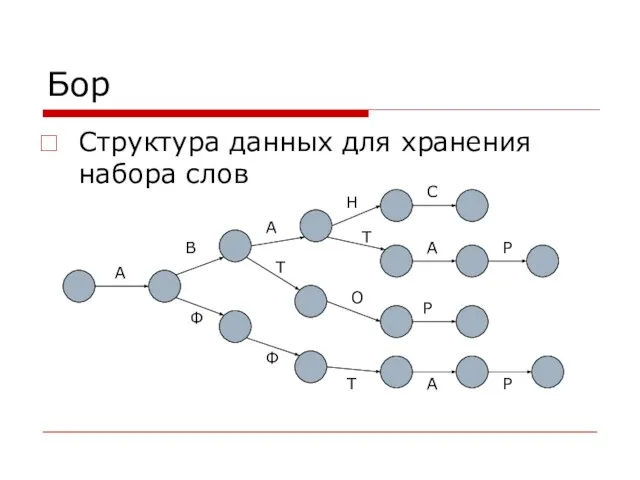
- 18. Бор Структура данных для хранения набора слов А В А Н С Т О Р А
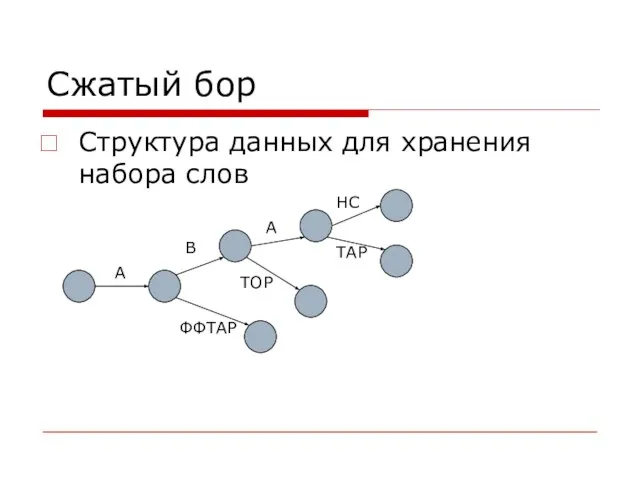
- 19. Сжатый бор Структура данных для хранения набора слов А В А НС ТОР ТАР ФФТАР
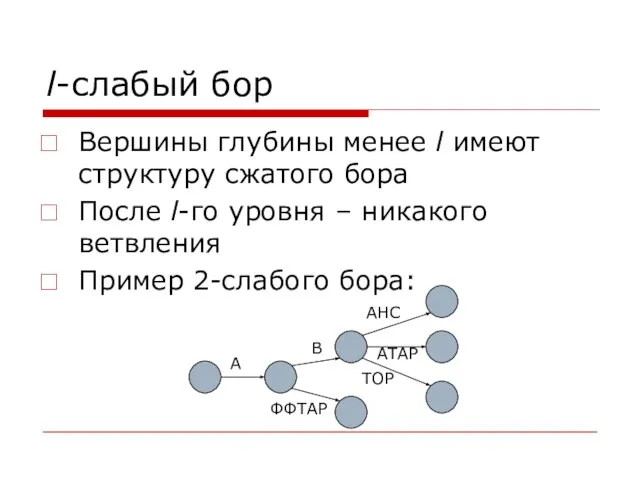
- 20. l-слабый бор Вершины глубины менее l имеют структуру сжатого бора После l-го уровня – никакого ветвления
- 21. Интервальные запросы Дан массив A длины n с целыми числами. Поступают запросы про числа в позициях
- 22. Интервальные запросы (2) RMQ – Range Minimum Query Запрос (i, j) – найти индекc l, такой
- 23. Интервальные запросы (3) BVRQ – Bounded Value Range Query Запрос (i, j, k) – найти множество
- 24. Часть III – Алгоритм Маасса-Новака Подход Маасса-Новака Случай d = 1 Общий случай Оценка времени поиска
- 25. Подход Маасса-Новака Старый подход №1: Выберем строку s из T. За время O(|P|d) можно сравнить ее
- 26. Подход Маасса-Новака Чем плохи старые подходы? Старый подход №1: Перебор всех строк из T - ВРЕМЯ
- 27. Подход Маасса-Новака Иногда: обнаружим один подходящий вариант и проверим его за O(|P|). Иногда: будем искать P
- 28. Случай d = 1 Пусть S – сжатый бор, содержащий все подстроки Т, h0 – высота
- 29. Случай d = 1 minprefs(P) > h0 Ищем P в боре S Доходим до листа Сверяем
- 30. Случай d = 1 minprefs(P) ≤ h0 Предподсчитаем все строки, отличающиеся от строк из T ровно
- 31. Общий случай Пусть P совпадает некоторой строкой s из S с d ошибками Если prefh0(P)=prefh0(s), дойдем
- 32. Общий случай (2) Снова два случая: minprefs(r)>h1 Дойдем в боре S’ до соответствующего листа, далее ”старый
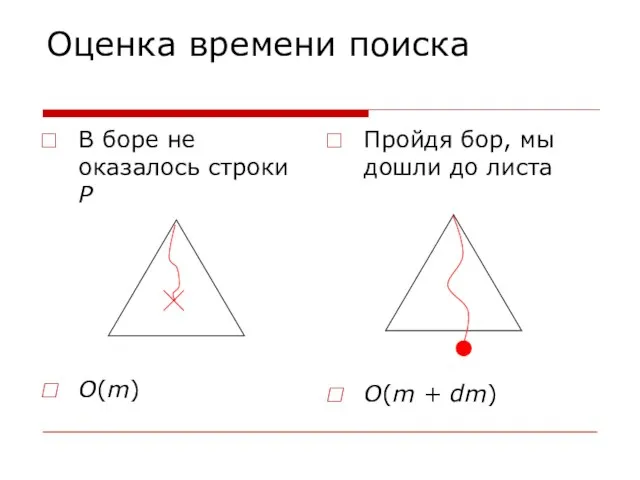
- 33. Оценка времени поиска В боре не оказалось строки P O(m) Пройдя бор, мы дошли до листа
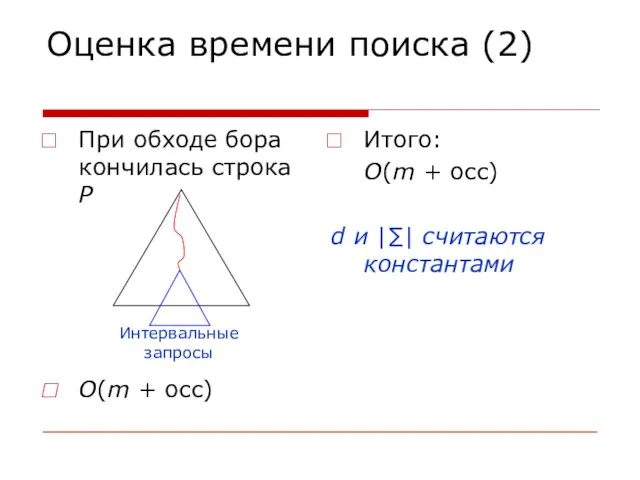
- 34. Оценка времени поиска (2) При обходе бора кончилась строка P O(m + occ) Итого: O(m +
- 35. Оценка времени индексирования Суммарный размер вспомогательных боров: O(h0h1…hd-1|S|) Время построения индекса: O(h0h1…hd|S|) hi=O(log n) В среднем
- 36. Использование интервальных запросов Необходимо за время O(occ) находить все первые позиции вхождений все документы, содержащие образец
- 37. Использование интервальных запросов (2) СRQ сводится к BVRQ Заведем массив B: B[i] = предыдущая позиция в
- 38. Использование интервальных запросов (3) BVRQ решается за время сведением к RMQ: Запрос (2,7,6): 2 4 4
- 40. Скачать презентацию



























![Использование интервальных запросов (2) СRQ сводится к BVRQ Заведем массив B: B[i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/387389/slide-36.jpg)

 Занятие для детей 6 – 7 лет с синдромом гиперактивности тема: «Мы - разные, мы - вместе».
Занятие для детей 6 – 7 лет с синдромом гиперактивности тема: «Мы - разные, мы - вместе». Анализ товарных и финансовых рынков
Анализ товарных и финансовых рынков Привет (Hello)
Привет (Hello) Химическая авария
Химическая авария The Story of St. Valentine (История святого Валентина)
The Story of St. Valentine (История святого Валентина) Icons Webshop Promodomo
Icons Webshop Promodomo Компания FINFIRE
Компания FINFIRE «Педагогическая технология – это описание процесса достижения планируемых результатов обучения»
«Педагогическая технология – это описание процесса достижения планируемых результатов обучения»  Презентация на тему Религия (11 класс)
Презентация на тему Религия (11 класс) Невская битва
Невская битва 1C:Смета
1C:Смета Биография семьи в биографии страны
Биография семьи в биографии страны Конституция России
Конституция России Порядок применения льгот по налогу на доходы (прибыль) для микрокредитных организаций
Порядок применения льгот по налогу на доходы (прибыль) для микрокредитных организаций Информационная эвристика в Интернет(опыт специального курса на историческом факультете МГУ)
Информационная эвристика в Интернет(опыт специального курса на историческом факультете МГУ) Психическая травма у детей: особенности проявления и психологическая помощь
Психическая травма у детей: особенности проявления и психологическая помощь Реакции ионного обмена (8 класс)
Реакции ионного обмена (8 класс) Эндокринология беременности
Эндокринология беременности 14_10_2022
14_10_2022 Зимние виды спорта
Зимние виды спорта Сертификация. Лекция №3
Сертификация. Лекция №3 Развитие сплоченности
Развитие сплоченности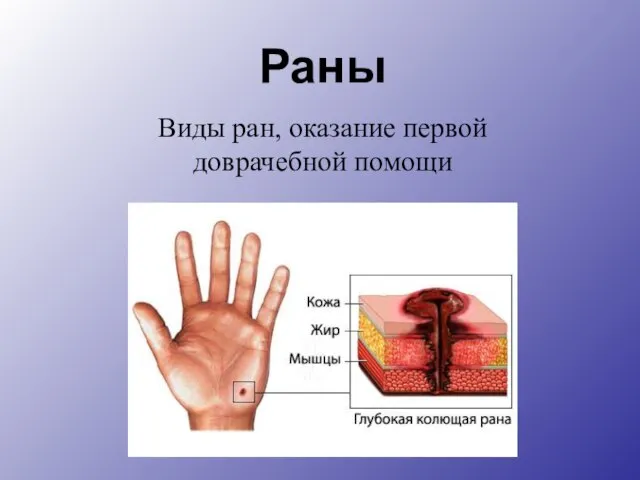 Презентация на тему Раны Виды ран оказание первой доврачебной помощи
Презентация на тему Раны Виды ран оказание первой доврачебной помощи  Повторим орфографию. (для подготовки К ЕГЭ) Проверяемые безударные гласные. П…льба,ум… лять зн..чение, бл…госл…вить, обн…жать, по
Повторим орфографию. (для подготовки К ЕГЭ) Проверяемые безударные гласные. П…льба,ум… лять зн..чение, бл…госл…вить, обн…жать, по Презентация на тему Что такое планета
Презентация на тему Что такое планета Уровневая модель методической системы школы
Уровневая модель методической системы школы КОРПОРАЦИЯ ПО РАЗВИТИЮ И ПРОДВИЖЕНИЮ ЭКСПОРТА
КОРПОРАЦИЯ ПО РАЗВИТИЮ И ПРОДВИЖЕНИЮ ЭКСПОРТА Аккредитив
Аккредитив