Задачи на построение

Введение
Геометрические инструменты
школьника и инженера
1.Линейка.
2.Циркуль.
3.Транспортир.

Набор инструментов

Набор инструментов

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую через две данные точки;
с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

План решения задачи на построение.
Анализ ( нахождение связи между
элементами геометрической фигуры).
Построение с обязательным описанием хода его выполнения.
Доказательство получения искомой фигуры.
Исследование.

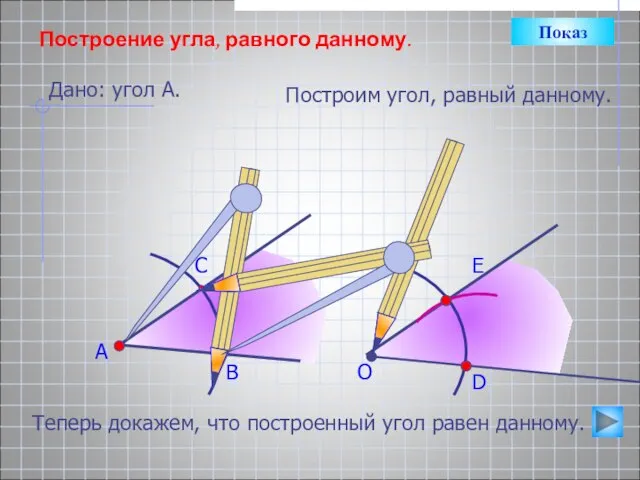
А
В
С
Построение угла, равного данному.
Дано: угол А.
Построим угол, равный данному.
О
D
E
Теперь докажем, что построенный угол равен данному.
Показ

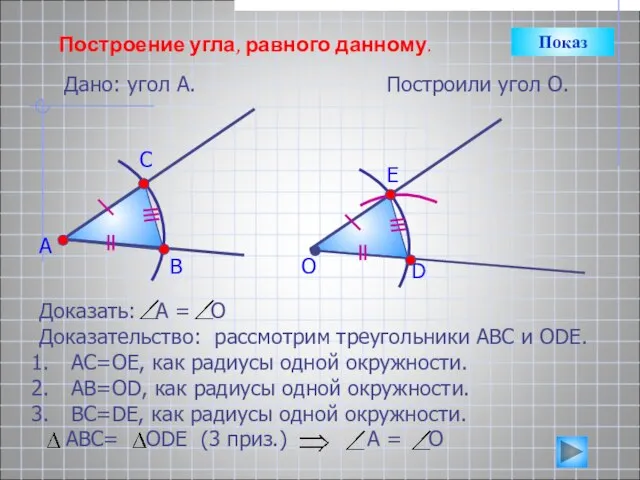
Построение угла, равного данному.
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А = О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы одной окружности.
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Показ

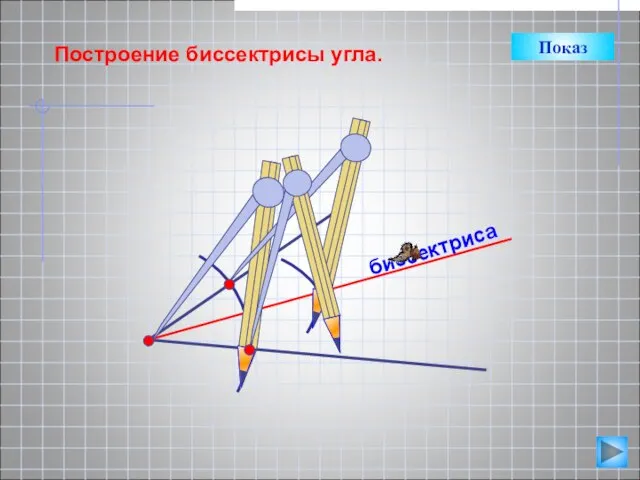
биссектриса
Построение биссектрисы угла.
Показ

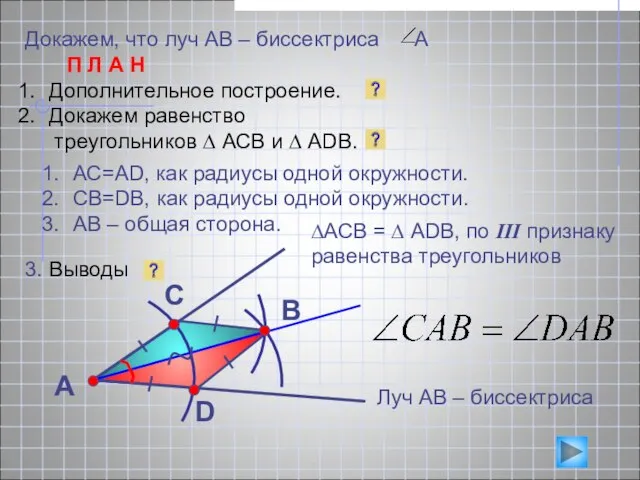
Докажем, что луч АВ – биссектриса А
П Л А Н
Дополнительное построение.
Докажем равенство
треугольников ∆ АСВ и ∆ АDB.
3. Выводы
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
?
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
?
?

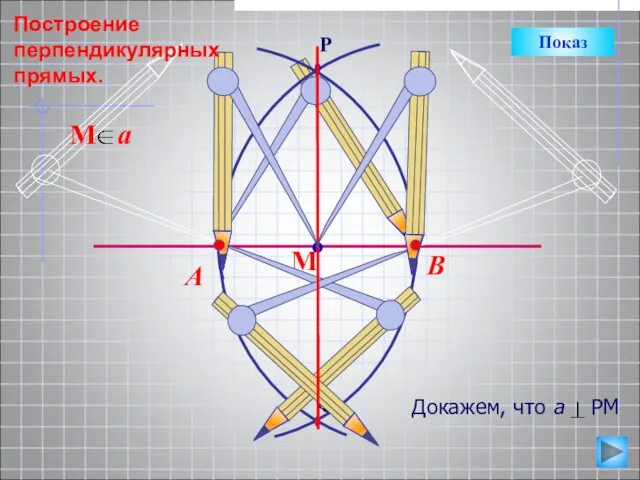
В
А
Показ
Построение
перпендикулярных
прямых.

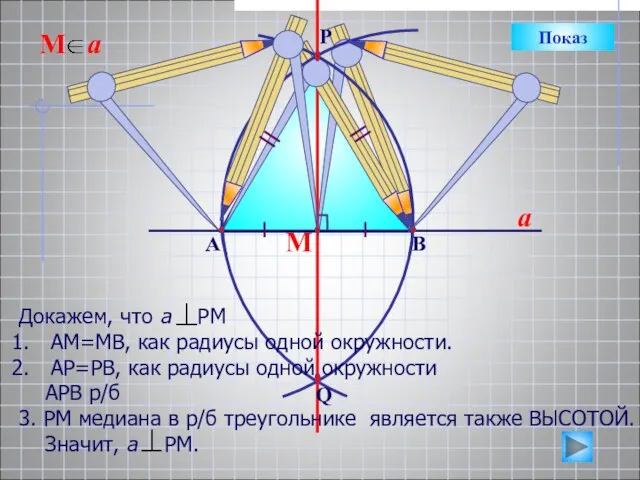
М
a
Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как радиусы одной окружности АРВ р/б
3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.
Значит, а РМ.
Показ

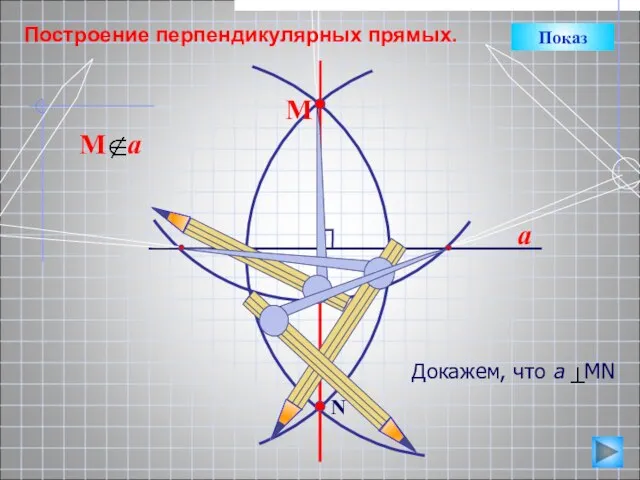
a
N
М
Построение перпендикулярных прямых.
Показ

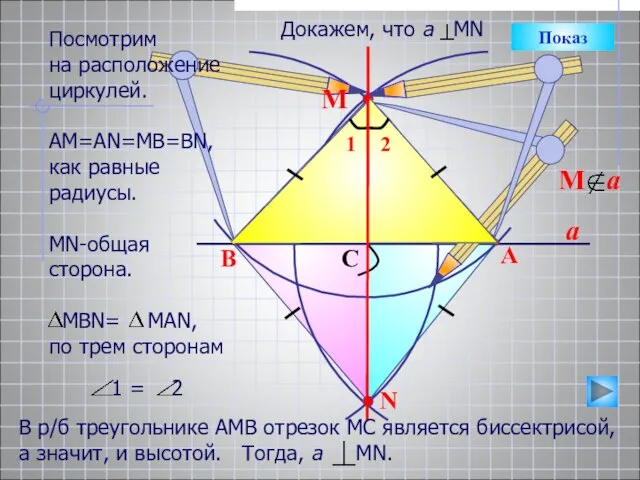
a
N
B
A
C
М
Показ
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN= MAN,
по трем сторонам

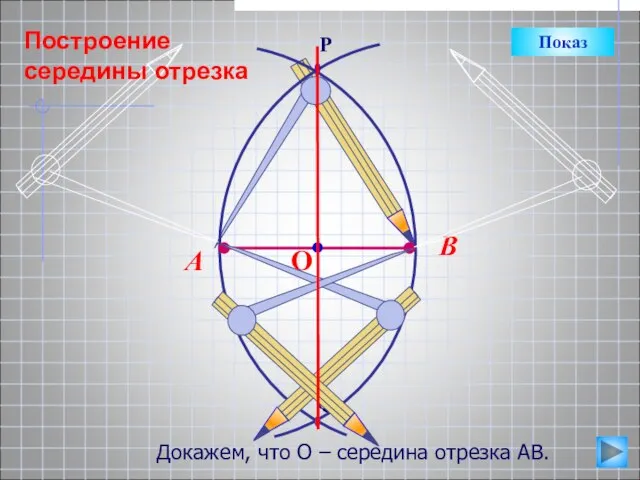
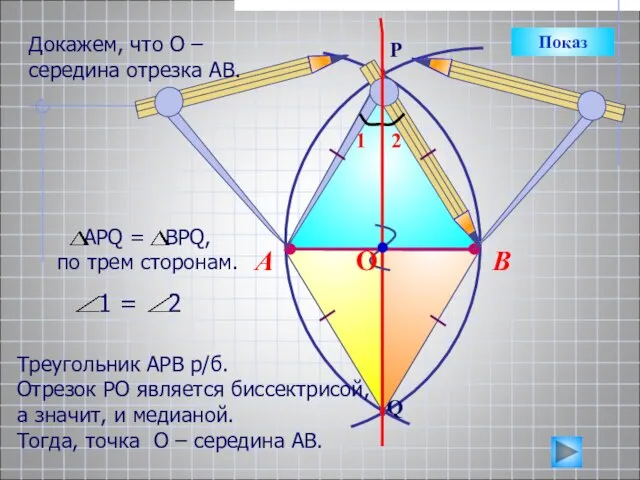
Докажем, что О – середина отрезка АВ.
Показ
Построение
середины отрезка

В
А
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.
Тогда, точка О – середина АВ.
Показ
Докажем, что О –
середина отрезка АВ.

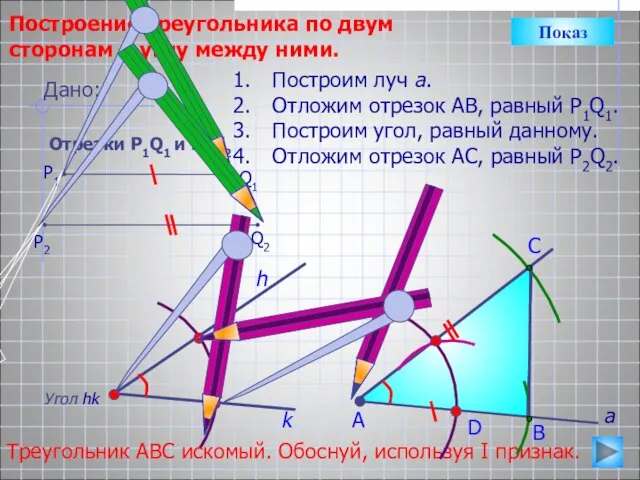
D
С
Построение треугольника по двум сторонам и углу между ними.
Угол hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному.
Отложим отрезок АС, равный P2Q2.
В
А
Треугольник АВС искомый. Обоснуй, используя I признак.
Дано:
Отрезки Р1Q1 и Р2Q2
Q1
P1
P2
Q2
а
k
Показ

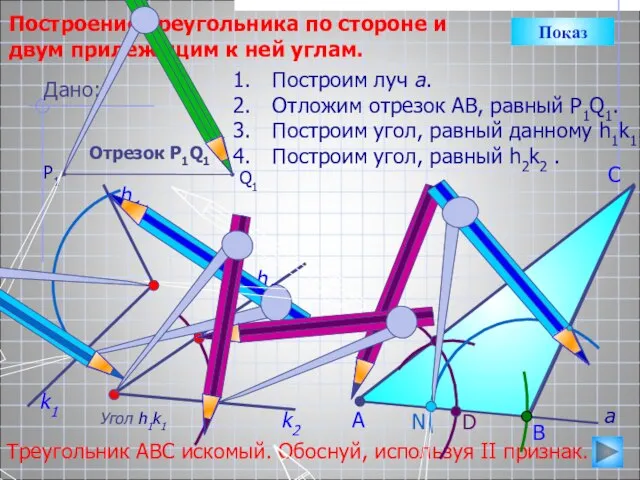
D
С
Построение треугольника по стороне и двум прилежащим к ней углам.
Угол h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному h1k1.
Построим угол, равный h2k2 .
В
А
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
Показ
h1
k1
N

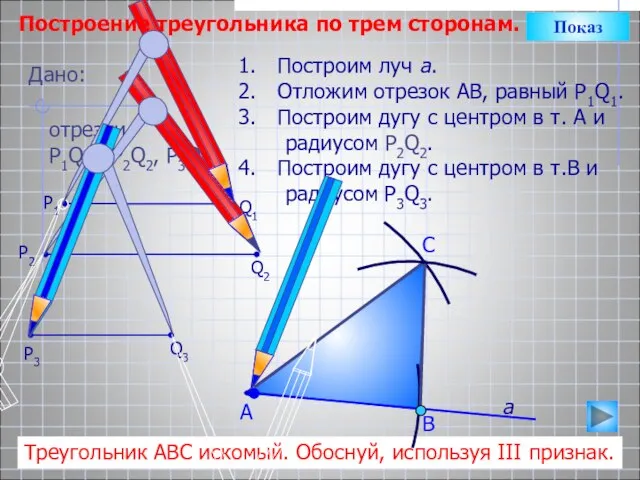
С
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром в т. А и
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
В
А
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Показ
Построение треугольника по трем сторонам.

Методы решения задач на построение
1.Метод анализа.
2.Метод подобия.
3.Метод геометрических мест.

НЕРАЗРЕШИМЫЕ ЗАДАЧИ
Квадратура круга - построение
квадрата , равновеликого
данному кругу с помощью циркуля
и линейки

НЕРАЗРЕШИМЫЕ НЕРАЗРЕШИМЫЕ
ЗАДАЧИ
ТРИСЕКЦИЯ УГЛА – деление данного угла на три равных части с помощью циркуля и
линейки.

НЕРАЗРЕШИМЫЕ ЗАДАЧИ
УДВОЕНИЕ КУБА – построение
ребра куба , объем которого вдвое больше объема данного
куба,
с помощью циркуля и линейки.