ИНФОРМАЦИОННАЯ ЧУВСТВИТЕЛЬНОСТЬ КОМПЬЮТЕРНЫХ АЛГОРИТМОВ И ЕЁ КОЛИЧЕСТВЕННЫЕ МЕРЫ

ТРЕБОВАНИЯ РАЗРАБОТЧИКОВ АЛГОРИТМИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПРОГРАММ
Ресурсная эффективность по трудоёмкости и дополнительной памяти
Прогнозирование временных характеристик на реальном диапазоне длин входов
Обеспечение стабильности по времени на различных входах фиксированной длины

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
А – алгоритм;
DA – множество возможных конкретных проблем для задачи, решаемой с помощью алгоритма А
(множество допустимых входов алгоритма);
D – конкретный вход алгоритма;
fA(D) – функция трудоёмкости для входа D;

ПРОГНОЗИРОВАНИЕ НА ОСНОВЕ ФУНКЦИИ ТРУДОЁМКОСТИ:
НЕДОСТАТКИ СУЩЕСТВУЮЩИХ ПОДХОДОВ
Прогнозирование по трудоёмкости в худшем случае (гарантированная оценка сверху) даёт почти всегда сильно завышенные результаты
Прогнозирование по трудоёмкости в среднем не учитывает информацию о размахе варьирования.
Качество прогноза во многом определяется влиянием различных входов фиксированной длины на трудоёмкость, информационной чувствительностью исследуемого алгоритма в рамках выбранной количественной оценки.

ПОСТАНОВКА ЗАДАЧИ И ПРЕДПОЛОЖЕНИЯ
Задача: Введение и сравнительный анализ различных количественных оценок информационной чувствительности.
Предположения:
1. Трудоёмкость алгоритма на входах фиксированной длины - дискретная ограниченная случайная величина.
2. Выбор распределения, аппроксимирующего функцию трудоёмкости производится на основе экспериментальных исследований.

ГИСТОГРАММА ОТНОСИТЕЛЬНЫХ ЧАСТОТ ДЛЯ АЛГОРИТМА УМНОЖЕНИЯ ДЛИННЫХ ЦЕЛЫХ ЧИСЕЛ В СТОЛБИК (N=100).

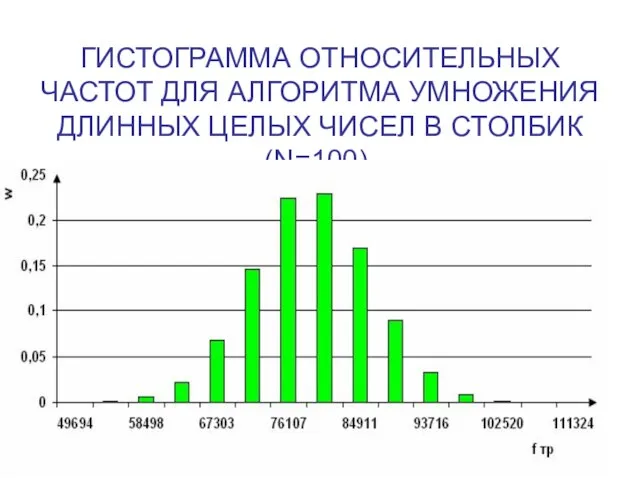
ГИСТОГРАММА ОТНОСИТЕЛЬНЫХ ЧАСТОТ ТРУДОЁМКОСТИ ДЛЯ АЛГОРИТМА СОРТИРОВКИ ВСТАВКАМИ ПРИ N=100, M=20000

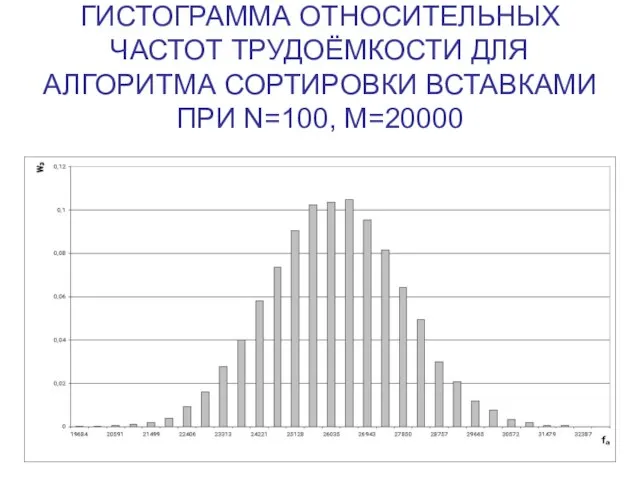
ГИСТОГРАММА ОТНОСИТЕЛЬНЫХ ЧАСТОТ ЗНАЧЕНИЙ ФУНКЦИИ ТРУДОЕМКОСТИ ДЛЯ АЛГОРИТМА КНУТА-МОРРИСА-ПРАТТА,
N=10000, M-20.

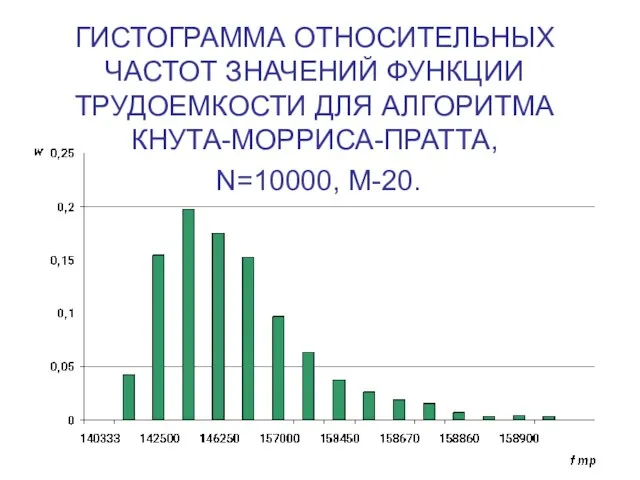
ПОНЯТИЕ ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ
Впервые понятие информационной чувствительности алгоритма по трудоёмкости введено М. В. Ульяновым и В. А. Головешкиным. Понятие «информационная чувствительность» отражает тот факт, что алгоритм задаёт различное число базовых операций принятой модели вычислений на разных входах , имеющих фиксированную длину . Ключевым для содержательной интерпретации этого термина является выбор количественной оценки (меры), обладающей свойством сопоставимости, т. е. дающей возможность решения задач сравнения алгоритмов и их рационального выбора.

ОЦЕНКА ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ ПО ЭНТРОПИИ
Для дискретной случайной величины
Непрерывный аналог - дифференциальная энтропия
Проблемы: не чувствительность к положению моды, максимум для ограниченной случайной величины – при равномерном распределении, влияние на энтропийную оценку числа сегментов гистограммы

СТАТИСТИЧЕСКАЯ ОЦЕНКА ИНФОРМАЦИОННОЙ УВСТВИТЕЛЬНОСТИ
Нормированный (относительный) размах варьирования функции трудоемкости
Коэффициент вариации
- стандартное отклонение трудоемкости

СТАТИСТИЧЕСКАЯ ОЦЕНКА ИНФОРМАЦИОННОЙ УВСТВИТЕЛЬНОСТИ
Статистическая количественная оценка информационной чувствительности алгоритма по трудоёмкости
Её применение возможно в случае отсутствия знаний о законе распределения значений трудоёмкости или какой-либо его аппроксимации
Недостаток - она не позволяет указать интервал значений трудоёмкости при заданной вероятности,

КВАНТИЛЬНАЯ ОЦЕНКА ИНФОРМАЦИОННОЙ УВСТВИТЕЛЬНОСТИ
Основная идея состоит в определении длины сегмента нормированных значений трудоёмкости, по которому интеграл от функции плотности равен заданной вероятности (надёжности)
Отметим, так же, что эта оценка не содержит информацию о положении гамма-квантиля закона распределения на нормированном сегменте.

КВАНТИЛЬНАЯ МЕРА ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ – ИНТЕРВАЛ, СИММЕТРИЧНЫЙ ОТНОСИТЕЛЬНО МЕДИАНЫ РАСПРЕДЕЛЕНИЯ
.

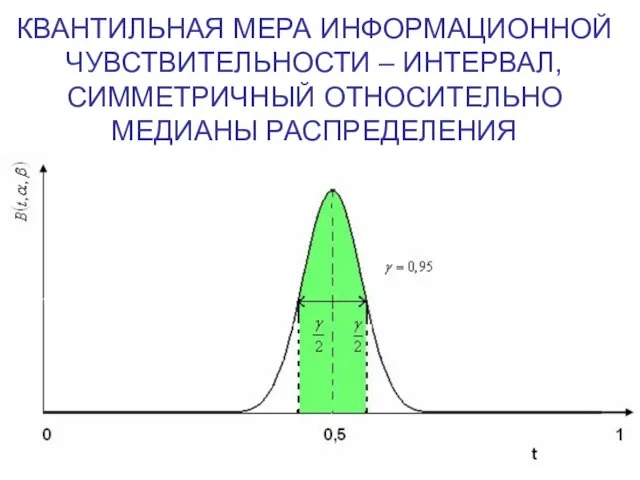
НОРМИРОВАННАЯ ВЕЛИЧИНА Т ДЛЯ АЛГОРИТМА УМНОЖЕНИЯ (N=100)

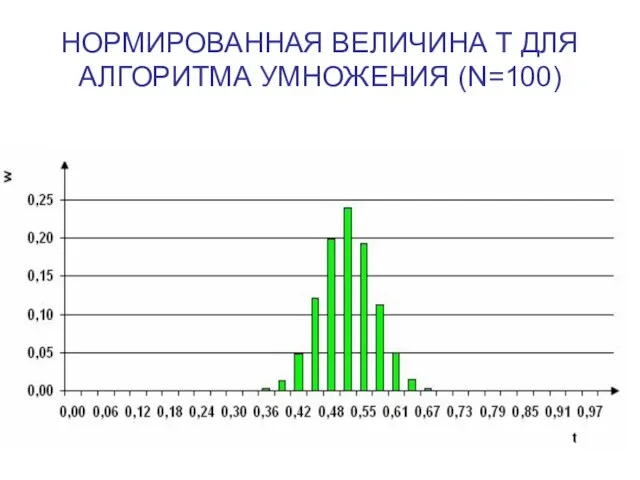
ВЫБОР ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
— гамма функция Эйлера
— параметры функции плотности бета-распределения

КОЛИЧЕСТВЕННАЯ МЕРА ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ
количественная мера информационной чувствительности является функцией от длины входа и вероятности.
- доверительная вероятность
- функция, обратная интегралу плотности распределения
- параметры бета-распределения

ЗАВИСИМОСТЬ ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ АЛГОРИТМА УМНОЖЕНИЯ ОТ ДЛИНЫ ВХОДА
ПРИ γ=0.95

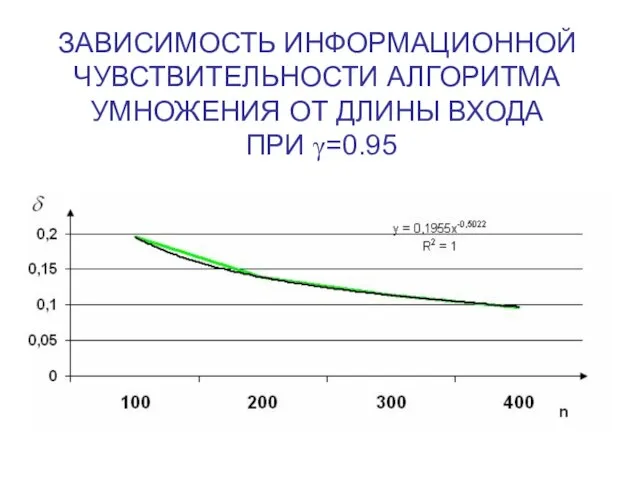
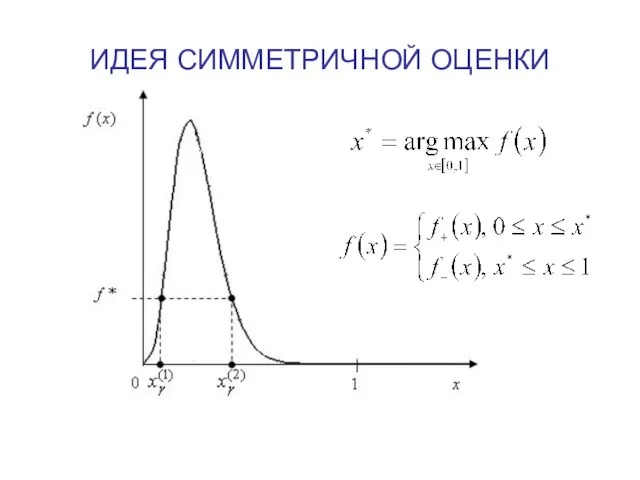
СИММЕТРИЧНАЯ ПО ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ОЦЕНКА
ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ
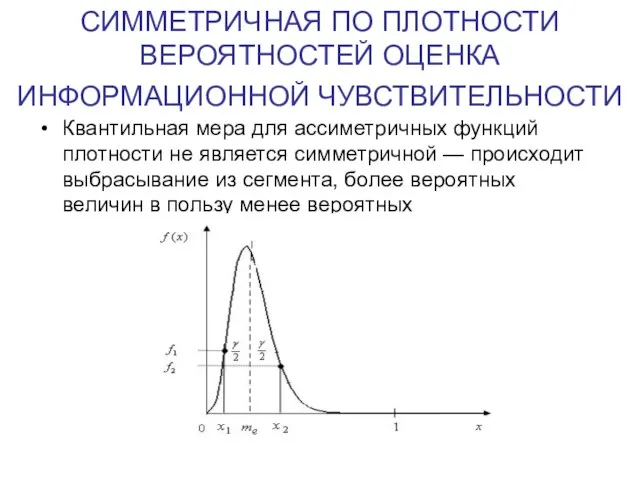
Квантильная мера для ассиметричных функций плотности не является симметричной — происходит выбрасывание из сегмента, более вероятных величин в пользу менее вероятных

ИДЕЯ СИММЕТРИЧНОЙ ОЦЕНКИ

СИММЕТРИЧНАЯ ПО ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ОЦЕНКА
ИНФОРМАЦИОННОЙ ЧУВСТВИТЕЛЬНОСТИ

МОДЕЛЬНЫЙ ПРИМЕР
Результаты экспериментального исследования алгоритма Кнута-Морриса-Пратта для поиска подстроки в строке
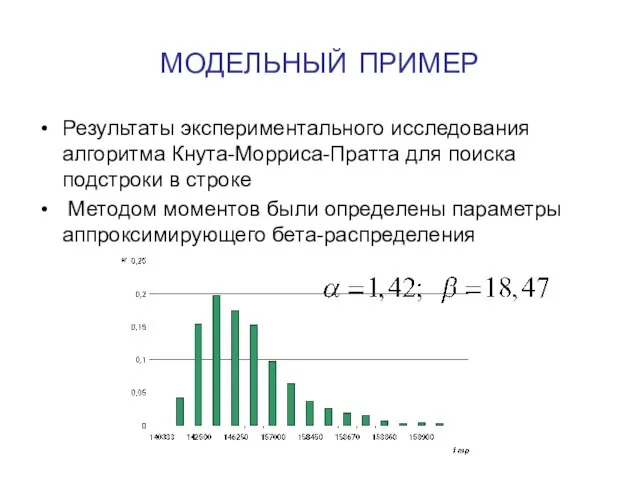
Методом моментов были определены параметры аппроксимирующего бета-распределения

МОДЕЛЬНЫЙ ПРИМЕР
Результаты расчётов:

ЗАКЛЮЧЕНИЕ
Введённая симметричная по плотности вероятностей количественная оценка информационной чувствительности может быть использована как более достоверная в случае асимметрии аппроксимирующей функции плотности при прогнозировании временной эффективности компьютерных алгоритмов, а также при решении задачи рационального выбора алгоритмов по критерию стабильности по времени, равно как и при решении других задач прикладной теории алгоритмов