Курс «Алгебра и начала анализа»

Аннотация
Данная презентация предназначена для проведения урока алгебры
и начала анализа в 11 классе по теме: «Первообразная. Интеграл.»
Цель урока:
закрепление свойств первообразной, умение пользоваться таблицей
первообразных, правилами нахождения первообразных, отработка
вычислительных навыков интегралов, проверка умения в построении
графиков, применение интегралов к вычислению площадей;
Подготовка к итоговой аттестации в форме и по материалам ЕГЭ.

Историческая справка
Вы познакомитесь в этой теме с самыми началами интегрального
исчисления, служащего продолжением уже известного вам
дифференциального исчисления.
Первые работы по открытию интегрального исчисления принадлежат еще
Архимеду – первому математику древности.
В средние века этой проблемой занимался итальянский ученый Кавальери.
Но подлинное открытие интегрального исчисления принадлежит двум великим
ученым XVII века – Ньютону и Лейбницу.
Исаак Ньютон
Готфрид Вильгельм
Лейбниц
Архимед
Бонавентура
Кавальери

Неопределенный интеграл
Операция, обратная дифференцированию, называется интегрированием.
Если мы ищем скорость пути, мы дифференцируем функцию s(t) и
получаем s’(t)=v(t). Если же функция v(t) нам известная, а требуется найти
функцию s(t), то мы будем интегрировать функцию v(t).
Чтобы хорошо разобраться в материале этой темы, нужно вспомнить, что
такое дифференцирование, геометрический смысл производной,
Механический смысл производной и формулы дифференцирования.
Дифференцирование - это операция нахождения производной,
если функция f(x) имеет производную в точке х0.
Сама функция называется дифференцируемой в этой точке.
Повторение пройденного материала

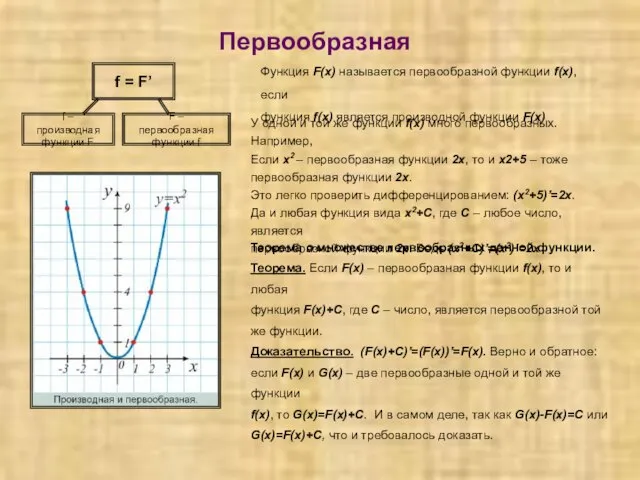
Первообразная
f = F’
f – производная
функции F
F – первообразная
функции f
Функция F(x) называется первообразной функции f(x), если
функция f(x) является производной функции F(x)
У одной и той же функции f(x) много первообразных. Например,
Если х2 – первообразная функции 2х, то и х2+5 – тоже
первообразная функции 2х.
Это легко проверить дифференцированием: (х2+5)’=2х.
Да и любая функция вида х2+С, где С – любое число, является
первообразной функции 2х. Ведь (х2+С)’=(х2)’=2х
Теорема о множестве первообразных данной функции.
Теорема. Если F(x) – первообразная функции f(x), то и любая
функция F(x)+C, где С – число, является первообразной той
же функции.
Доказательство. (F(x)+C)’=(F(x))’=F(x). Верно и обратное:
если F(x) и G(x) – две первообразные одной и той же функции
f(x), то G(x)=F(x)+C. И в самом деле, так как G(x)-F(x)=C или
G(x)=F(x)+C, что и требовалось доказать.

Неопределенный интеграл
Неопределенным интегралом функции f(x) называется множество первообразных этой функции.
Неопределенный интеграл функции f(x) обозначается символом ∫f(x)dx. Знак дифференциала dx
указывает, какая переменная, входящая в выражение f(x), является аргументом.
Например, ∫abdb – интеграл показательной функции, ∫abda – интеграл степенной функции.
Первый равен
а второй равен
Чтобы найти интеграл от данной функции, нужно найти любую ее первообразную и прибавить
к ней произвольное число С.
Так,

Три правила интегрирования
Техника интегрирования – сложный раздел математики. В нем сделали свои открытия такие
корифеи, как Эйлер, Лобачевский, Коши, Остроградский.
Вам предстоит ознакомиться с тремя самыми простыми правилами интегрирования.

Первое правило интегрирования:
Интеграл суммы двух функций равен сумме интегралов этих функций: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx.
Доказательство: Пусть F(x) и G(x) – первообразные функций f(x) и g(x). Тогда P(x)=f(x), G’(x)=g(x).
Но известно, что (F(x)+G(x))’=P(x)+G’(x), то есть (F(x)+G(x))’=f(x)+g(x). Тем самым доказано, что
функция F(x)+G(x)-первообразная функции f(x)+g(x). Отсюда получаем ∫(f(x)+g(x))dx=F(x)+G(x)+C1,
∫(f(x)dx+∫g(x))dx=F(x)+C2+G(x)+C3. И так как С1, С2 и С3 – произвольные числа, то окончательно
имеем: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx, что и требовалось доказать.
Три правила интегрирования
Второе правило интегрирования:
Постоянный множитель можно вынести за знак интеграла: ∫cf(x)dx=c∫f(x)dx.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда P(x)=f(x), а значит, cP(x)=cf(x),
откуда и следует доказываемое равенство.
Третье правило интегрирования:
Если F(x) первообразная функции f(x), k≠0, то
Доказательство:
Пусть F(x) первообразная функции f(x). Тогда P(x)=f(x), а P(kx+b)=f(kx+b)k, откуда и получается
доказываемое равенство.

Определенный интеграл
Пусть ∫v(t)dt = s(t) + C. Зная это, можно найти путь, пройденный от момента времени а до момента
времени b. Путь равен разности значений функций s при t=b и при t=a, то есть (s(b)+C) - (s(a)+C).
При этом безразлично, какую из первообразных мы возьмем: ведь (s(b) + C) – (s(a) + C)=s(b) - s(a).
Моделью интеграла может служить не только формула пути, но и формула площади любой плоской
фигуры.
Разбиение плоской фигуры на криволинейные трапеции
Итак, перед нами стоит задача научиться находить площадь
плоской фигуры. Фигура определяется ограничивающей ее
линией. Если эта линия состоит из прямолинейных отрезков, то
ее площадь – площадь многоугольника, которую можно найти деля
фигуру на прямоугольники и треугольники. Плохо, если фигура со
всех сторон ограничена кривыми. Но в этом случае ее можно
разбить на более мелкие фигуры, ограниченные с трех сторон
прямыми, пересекающимися под прямыми углами. И только с
одной стороны такие фигуры будут иметь неустранимо
криволинейную границу.
Разбиение плоской фигуры
на криволинейные трапеции

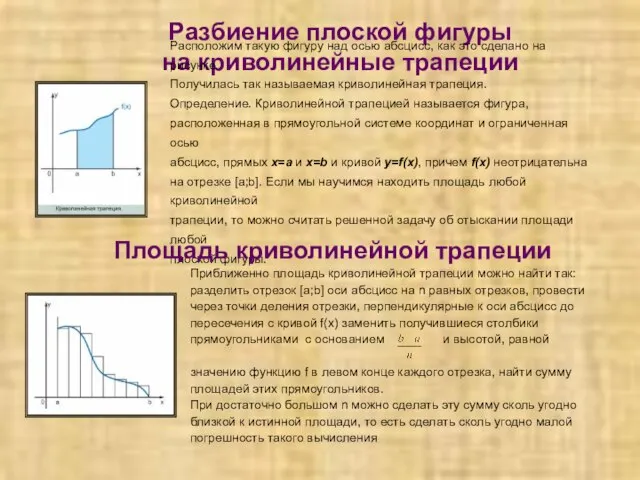
Разбиение плоской фигуры
на криволинейные трапеции
Расположим такую фигуру над осью абсцисс, как это сделано на рисунке.
Получилась так называемая криволинейная трапеция.
Определение. Криволинейной трапецией называется фигура,
расположенная в прямоугольной системе координат и ограниченная осью
абсцисс, прямых х=а и x=b и кривой y=f(x), причем f(x) неотрицательна
на отрезке [a;b]. Если мы научимся находить площадь любой криволинейной
трапеции, то можно считать решенной задачу об отыскании площади любой
плоской фигуры.
Площадь криволинейной трапеции
Приближенно площадь криволинейной трапеции можно найти так:
разделить отрезок [a;b] оси абсцисс на n равных отрезков, провести
через точки деления отрезки, перпендикулярные к оси абсцисс до
пересечения с кривой f(x) заменить получившиеся столбики
прямоугольниками с основанием и высотой, равной
значению функцию f в левом конце каждого отрезка, найти сумму
площадей этих прямоугольников.
При достаточно большом n можно сделать эту сумму сколь угодно
близкой к истинной площади, то есть сделать сколь угодно малой
погрешность такого вычисления

Площадь криволинейной трапеции
Можно найти площадь криволинейной трапеции и совершенно
точно, пользуясь результатом, полученным в конце XVII века
независимо друг от друга двумя великими учеными Ньютоном
и Лейбницем.
Для доказательства формулы, носящей их имена, докажем, что
площадь криволинейной трапеции равна F(b)-F(a), где
F- любая из первообразных функции f, график которой
ограничивает криволинейную трапецию
Теперь вычисление площади криволинейной трапеции
будем записывать так:
1) Найдем любую из первообразных F функции f.
2) Запишем
Формула и называется формулой Ньютона –Лейбница.

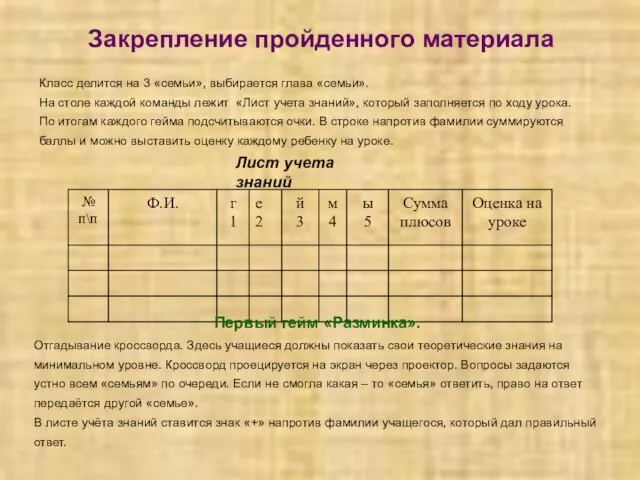
Закрепление пройденного материала
Класс делится на 3 «семьи», выбирается глава «семьи».
На столе каждой команды лежит «Лист учета знаний», который заполняется по ходу урока.
По итогам каждого гейма подсчитываются очки. В строке напротив фамилии суммируются
баллы и можно выставить оценку каждому ребенку на уроке.
Лист учета знаний
Первый гейм «Разминка».
Отгадывание кроссворда. Здесь учащиеся должны показать свои теоретические знания на минимальном уровне. Кроссворд проецируется на экран через проектор. Вопросы задаются устно всем «семьям» по очереди. Если не смогла какая – то «семья» ответить, право на ответ передаётся другой «семье».
В листе учёта знаний ставится знак «+» напротив фамилии учащегося, который дал правильный ответ.

1.Как называется функция
F(x)?
2. Что является графиком
функции y = ax + b?
3. Самая низкая школьная
оценка.
4. Какой урок проходит
обычно перед зачетом?
5. Синоним слова «дюжина».
6. Есть в каждом слове у
растения и может быть у
уравнения.
7. Что можно вычислить
при помощи интеграла?
8. Одно из важнейших понятий
в математике?
9. Форма урока, на котором
проводится проверка знаний?
10. Немецкий ученый, в честь которого названа формула, связывающая площадь
криволинейной трапеции и интеграл.
11. Конь – лошадь – жеребенок, бык – корова – телёнок, король – королева – принц,
граф – графиня - …. .
12. Соответствие между множествами X и Y, при котором каждому значению
из множества X поставлено в соответствии единственное значение из множества Y ,
носит название ……..?

Второй гейм «Дальше, дальше…»
Этот гейм индивидуальный, т.е. каждый учащийся пишет ответы в своей тетради
(ответы должны дать за 15 минут).
1) Что называются интегралом ?
2) Что называется первообразной ?
3) Как читается основное свойство первообразной ?
4) Верно ли, что интеграл от любой степенной функции будет снова степенной функцией?
5) F’(x)=f(x) - как это можно прочесть?
6) Как можно вычислить площадь криволинейной трапеции при помощи интеграла?
7) Запишите с помощи интегралов площадь фигур, изображенных на рисунках?
Y
X
0
A
B
Y=F(x)
Y
0
X
F
Y=(x+3)/2

8. Найти первообразные для функций:
б).
д)
в).
г).
е)
9. Истинны ли равенства: б)
в)
г)
д)
е)
а)
а)
Ответы зачитываются сразу же. Правильный ответ учащиеся обводят в кружок и подсчитывают
Количество баллов и заносят в «Лист учета знаний»
Третий гейм «Спешите видеть»
Каждая команда за 5 минут должна изобразить криволинейную трапецию, ограниченную:
а) графиком функции у=(х+1)2, осью ОХ и прямой у=1-х
б) графиком функции у=4х-х2, с осью ОХ и прямой у=4-х
в) графиком функции у=4-х2, с осью ОХ и прямой у=4-х
За верное построение команды получают баллы

Четвертый гейм «Составь фразу»
Вычислите интеграл:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)

Ответы:
(-2) – З; 0 – Т; 1,5 – Д; 2 – Р; 4 – О; 6 – И; 6,2 – Ж; 9 – Ь;
10,5 – Н; 18 – Е; 24,2 – К; 48 – Л; 63,75 - Ю
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
ж и з н ь и д о в е р и е т е р я ю
19 20 21 22 23 24 25 26 27 28
т т о л ь к о р а з

Пятый гейм «Гонка за лидером»
Каждая»Семья» получает карточку. В каждой карточке по два задания: одно – в форме теста,
другое – своеобразный кроссворд.
За верно решенные задания в карточке «семья» получает 2 балла.
Карточка 1.
Задание 1. Для функции f(x)=ex найти первообразную, график которой проходит через
точку М (0;2).
а) F(x) = e+3; б) F(x) = ex; в) F(x) = ex+1; г) F(x)=ex-1 Ответ: В
Задание 2.
Вычислить
интеграл
Вычислить
интеграл
Вычислить площадь фигуры,
ограниченной линиями
у=4-х2, у=х+2, у=0
?
32
+6*?
-2*?

Карточка 2.
Задание 1. Для функции найти
первообразную, график которой проходит
через точку М (4;5)
а) б)
в) г)
а) F(x) = √x+3; б) F(x)=2√x;
в) F(x)=2√x+3; г) F(x) = √x+5.
Ответ: Б
Задание 2.
Вычислить
интеграл
Вычислить
интеграл
Вычислить площадь фигуры,
ограниченной линиями
У=x2, y=6-x, y=0
?
2
+?
-3*?
Карточка 3.
Задание 1. Для функции
найти первообразную, график которой
проходит через точку М (1;3)
Ответ: В
Вычислить
интеграл
Вычислить
интеграл
Задание 2.
Вычислить площадь фигуры,
ограниченной линиями
У=x2+1, х=-2-x, х = 2, y=0.
+3*?
+?
3*?
28