Слайд 2Consider the area under a curve
The area under a curve can be
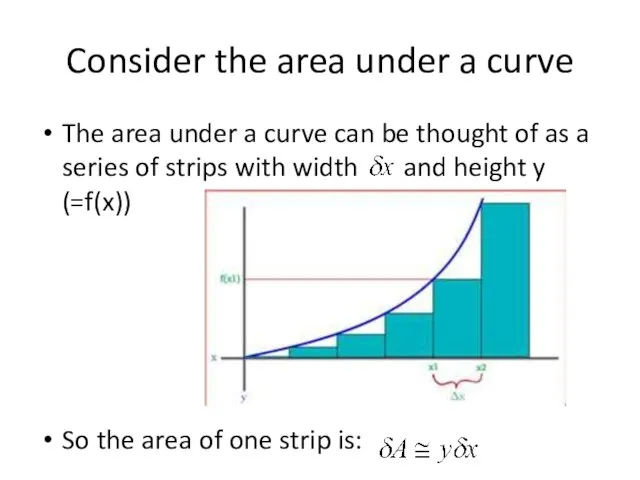
thought of as a series of strips with width and height y (=f(x))
So the area of one strip is:
Слайд 3Consider the area under a curve
Now consider the graph:
The total area between

the boundary values of x=a and x=b is:
Since the strip is an approximation of the area under the curve, the area of the strip approaches the area under the curve as
So,
Слайд 4Consider the area under a curve
Now consider an alternative expression for A:
Considering

the same starting point of:
Then:
Again this approximation becomes more accurate as:
So,
Слайд 5Consider the area under a curve
So,
But,
So between x=a and x=b:





 СОТРУДНИЧЕСТВО С КНР ОПЫТ ВТБ МАРТ 2011
СОТРУДНИЧЕСТВО С КНР ОПЫТ ВТБ МАРТ 2011 Профессия «Парикмахер»,специальность «Парикмахерское искусство» Мастерские –лаборатории: Салон-парикмахерская, мастер
Профессия «Парикмахер»,специальность «Парикмахерское искусство» Мастерские –лаборатории: Салон-парикмахерская, мастер Электронная почта: основные тенденции развития
Электронная почта: основные тенденции развития «След войны в моей семье»
«След войны в моей семье» Презентация на тему Знаки «+», «–»,«=»
Презентация на тему Знаки «+», «–»,«=»  Интерактивная версия медиа справочника «Скорый помощник»
Интерактивная версия медиа справочника «Скорый помощник» Коммерческая ипотека Илья Шершнев, Директор по развитию.
Коммерческая ипотека Илья Шершнев, Директор по развитию. ситуации
ситуации День космонавтики
День космонавтики Жүрек және қан тамырларды
Жүрек және қан тамырларды  Сырьевая проблема
Сырьевая проблема Сибирский ботанический сад Томского университета
Сибирский ботанический сад Томского университета Прогулки с динозаврами - презентация для начальной школы_
Прогулки с динозаврами - презентация для начальной школы_ Великие химики
Великие химики ОЛИМПИАДА – МОСКВА 1980
ОЛИМПИАДА – МОСКВА 1980 Презентация на тему Догосударственный период в истории восточных славян
Презентация на тему Догосударственный период в истории восточных славян  Презентация на тему Животноводство в нашем крае (4 класс)
Презентация на тему Животноводство в нашем крае (4 класс) 1 сентября День знаний
1 сентября День знаний Техника безопасности в компьютерном классе
Техника безопасности в компьютерном классе Конкурс«Эра фантастики»
Конкурс«Эра фантастики» Нурсултан Назарбаев
Нурсултан Назарбаев  Озеро Байкал (8 класс)
Озеро Байкал (8 класс) Русский традиционный мужской костюм
Русский традиционный мужской костюм Исследование рынка детских психологических услуг в Санкт-Петербурге
Исследование рынка детских психологических услуг в Санкт-Петербурге Радио „Эхо Москвы в Томске“
Радио „Эхо Москвы в Томске“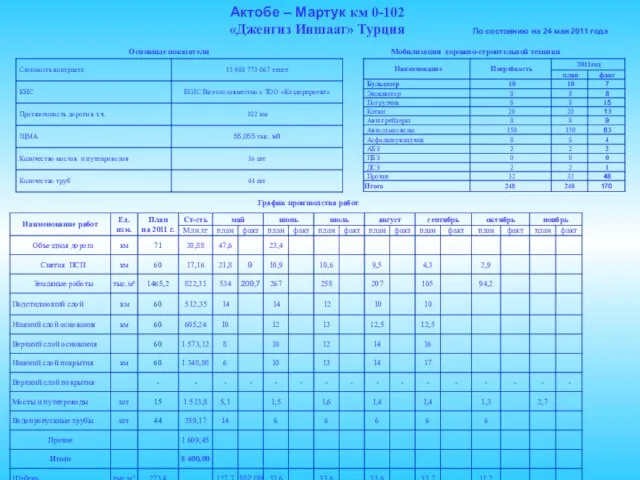 Актобе – Мартук км 0-102 «Дженгиз Иншаат» Турция
Актобе – Мартук км 0-102 «Дженгиз Иншаат» Турция Презентация Microsoft PowerPoint (2)
Презентация Microsoft PowerPoint (2) Лёгкая атлетика. Многоскоки
Лёгкая атлетика. Многоскоки