Слайд 2Ударное взаимодействие тел
Закон сохранения механической энергии и закон сохранения импульса позволяют находить

решения механических задач в тех случаях, когда неизвестны действующие силы.
Примером такого рода задач является ударное взаимодействие тел.
Слайд 3Определение удара
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого

их скорости испытывают значительные изменения.
Слайд 4Применение законов сохранения энергии и импульса
Во время столкновения тел между ними действуют

кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
Слайд 5Абсолютно упругий удар
Абсолютно упругий удар - столкновение, при котором сохраняется механическая энергия

системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Слайд 6Пример абсолютно упругого столкновения
Простым примером абсолютно упругого столкновения может быть центральный удар

двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Слайд 7Центральный удар
Центральный удар шаров - соударение, при котором скорости шаров до и

после удара направлены по линии центров.
Слайд 8Применение закона сохранения механической энергии
В общем случае массы m1 и m2 соударяющихся

шаров могут быть неодинаковыми.
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2=0, u1 и u2 – скорости шаров после столкновения.
Слайд 9Применение закона сохранения импульса
Закон сохранения импульса для проекций скоростей на координатную

ось, направленную по скорости движения первого шара до удара, записывается в виде:
m1υ1=m1u1+m2u2.








 Федеральный государственный образовательный стандарт общего начального образования второго поколения
Федеральный государственный образовательный стандарт общего начального образования второго поколения Деструктивные организации
Деструктивные организации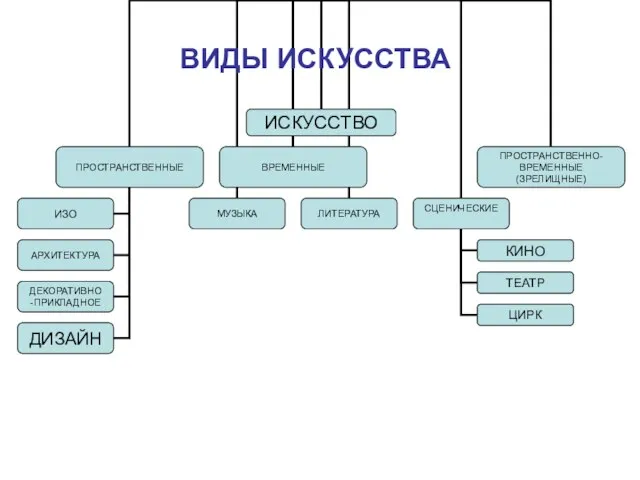 Виды искусства
Виды искусства Психоанализ и культура
Психоанализ и культура Основные законы управления
Основные законы управления Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат
Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма
План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма 220 лет РГПУ им. А.И.Герцена
220 лет РГПУ им. А.И.Герцена Презентация на тему Что изучает современная экология?
Презентация на тему Что изучает современная экология?  Экспорт нефти и нормативно-правовое регулирование
Экспорт нефти и нормативно-правовое регулирование Векторная алгебра
Векторная алгебра Физическое развитие детей и подростков (2)
Физическое развитие детей и подростков (2) Презентация на тему Франциск 1
Презентация на тему Франциск 1 Основные виды организационных структур
Основные виды организационных структур Tunti 8. Ruoka
Tunti 8. Ruoka Гражданственность
Гражданственность Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007
Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007 Волейбол
Волейбол Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий
Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи»
МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи» Презентация на тему Школьный референдум
Презентация на тему Школьный референдум Региональная инфраструктура сопровождения инновационных процессов в областной системе образования
Региональная инфраструктура сопровождения инновационных процессов в областной системе образования Русский народный праздник «Святки»
Русский народный праздник «Святки» Госбюджет. Внебюджетные фонды. Тема 6
Госбюджет. Внебюджетные фонды. Тема 6 Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе
Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе Доказательство теоремы Пифагора,основанного на теории подобия
Доказательство теоремы Пифагора,основанного на теории подобия Японская мифология
Японская мифология Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»
Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»